线性代数的学习和整理7:各种特殊效果矩阵特例(草稿-----未完成)
目录
1 矩阵
1.1 1维的矩阵
1.2 2维的矩阵
1.3 没有3维的矩阵---3维的是3阶张量
2 方阵
3 单位矩阵
3.1 单位矩阵的定义
3.2 单位矩阵的特性
3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]
3.4 零矩阵
3.4 看下这个矩阵 [0,1;1,0]
3.5 看下这个矩阵 [1,1;1,1]
4 镜像矩阵
5 旋转矩阵
6 伸缩矩阵 放大缩小倍数矩阵
7 剪切矩阵
1 矩阵
1.1 1维的矩阵
- 行向量,αT
- 列向量,α
行向量
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
\end{matrix}
\right]
$$
列向量
$$
\left[
\begin{matrix}
1 \\
4 \\
7
\end{matrix}
\right]
$$
1.2 2维的矩阵
- 一般2维表都可以看作矩阵。
- 矩阵的每个维度可以是1个数字,也可以是多个数字组成的数组/向量
- 比如 An*m就是n 行 m列的矩阵
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{matrix}
\right] \tag{1}
$$
1.3 没有3维的矩阵---3维的是3阶张量
- 比如3个坐标轴
1.4 下面本文总结的都是各种特殊效果矩阵特例
- 单位矩阵
- 零矩阵
- 等等
2 方阵: 正方形矩阵
- 行数和列数相等的矩阵即方阵
- 比如 An*n就是n 行 n列的矩阵
- 方阵有很多特殊的属性
- 比如虽然并不是,方阵一定有逆矩阵,但是可逆矩阵必须是方阵
$$
\left[
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix}
\right]
$$
3 单位矩阵
3.1 单位矩阵的定义
- 单位矩阵,一定是这样的[1,0;0,1]
- 单位矩阵的作用,矩阵A*I=A
- 矩阵 [1,0;0,1] 代表将其他矩阵 原样进行映射,不做任何改变
- 也就是单位矩阵,既不改变矩阵方向,也不改变伸缩矩阵的长短,完全不变
$$
\left[
\begin{matrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}
\right]
$$

3.2 单位矩阵的特性
- 单位矩阵的特性
- A*I=A
- A*A-=I
3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1]
- 因为 矩阵 [1,0;0,1] 代表将其他矩阵 原样进行映射,不做任何改变
- 而[1,1;1,1] 没有啥意义
- 可比较下面的结果,实际理解

3.4 零矩阵
- [0,0;0,0]
- 所有的列向量,都坍缩回原点
$$
\left[
\begin{matrix}
0 & 0 \\
0 & 0 \\
\end{matrix}
\right]
$$

3.4 看下这个矩阵 [0,1;1,0]
- [0,1;1,0]
- 这个矩阵,和单位矩阵形式恰好相反
- 从几何效果来看,是镜像矩阵(列向量互换了)
$$
\left[
\begin{matrix}
0 & 1 \\
1 & 0 \\
\end{matrix}
\right]
$$

3.5 看下这个矩阵 [1,1;1,1]
- [1,1;1,1]
- 几何效果是,矩阵的列向量会被变成完全相等(方向,长度都相等)
$$
\left[
\begin{matrix}
1 & 1 \\
1 & 1 \\
\end{matrix}
\right]
$$

4 镜像矩阵
- [0,1;1,0]
- 这个矩阵,和单位矩阵形式恰好相反
- 从几何效果来看,是镜像矩阵(列向量互换了)
$$
\left[
\begin{matrix}
0 & 1 \\
1 & 0 \\
\end{matrix}
\right]
$$

5 旋转矩阵
应该很多种把
6 伸缩矩阵 放大缩小倍数矩阵
- 把[1,0;0,1] 变成[2,0;0,1],即可实现伸缩效果
- 比如变成[2,0;0,1],是第1个列向量变长2倍
- 比如变成[1,0;0,-2],是第2个列向量变长2倍,且方向要相反(向原点的另外一边)
$$
\left[
\begin{matrix}
2 & 0 \\
0 & 1 \\
\end{matrix}
\right]
$$

7 剪切矩阵
相关文章:

线性代数的学习和整理7:各种特殊效果矩阵特例(草稿-----未完成)
目录 1 矩阵 1.1 1维的矩阵 1.2 2维的矩阵 1.3 没有3维的矩阵---3维的是3阶张量 2 方阵 3 单位矩阵 3.1 单位矩阵的定义 3.2 单位矩阵的特性 3.3 为什么单位矩阵I是 [1,0;0,1] 而不是[0,1;1,0] 或[1,1;1,1] 3.4 零矩阵 3.4 看下这个矩阵 [0,1;1,0] 3.5 看下这个矩阵…...

springBoot 配置文件 spring.mvc.throw-exception-if-no-handler-found 参数的作用
在Spring Boot应用中,可以通过配置文件来控制当找不到请求处理器(handler)时是否抛出异常。具体的配置参数是spring.mvc.throw-exception-if-no-handler-found。 默认情况下,该参数的值为false,即当找不到请求处理器时…...
linux部署kafka3.5.1(单机)
一、下载jdk17 kafka3.x版本需要jdk11以上版本才能更好的兼容,jdk11、jdk17都是LTS长期维护版本,而且jdk17支持springboot3.x,所以我选择了openjdk17。 下载地址: Archived OpenJDK GA Releaseshttps://jdk.java.net/archive/ 二、上传jdk安装包解压 …...

css 实现svg动态图标效果
效果演示: 实现思路:主要是通过css的stroke相关属性来设置实现的。 html代码: <svgt"1692441666814"class"icon"viewBox"0 0 1024 1024"version"1.1"xmlns"http://www.w3.org/2000/svg"p-id"…...
软件测试项目实战,电商业务功能测试点汇总(全覆盖)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 支付功能怎么测试…...

LeetCode[274]H指数
难度:Medium 题目: 给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。 根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指…...
MyBatis-Plus快速开始[MyBatis-Plus系列] - 第482篇
悟纤:师傅,MyBatis-Plus被你介绍的这么神乎其乎,咱们还是来的点实际的吧。 师傅:那真是必须的,学习技术常用的一种方法,就是实践。 悟纤:贱贱更健康。 师傅:这… 师傅:…...

CF1003A Polycarp‘s Pockets 题解
题目传送门 题目意思: 给你 n n n 个数,求出最多相同的数的个数。 这道题目有两种解法。 方法一:桶排 一边输入,一边将第 i i i 个数 a i a_i ai 出现的次数存在一个数组 b b b 的第 a i a_i ai 个位置。输入完后遍历…...

数据库厂商智臾科技加入龙蜥社区,打造多样化的数据底座
近日,浙江智臾科技有限公司(以下简称“智臾科技”)正式签署 CLA 贡献者许可协议,加入龙蜥社区(OpenAnolis)。 智臾科技主创团队从 2012 年开始投入研发 DolphinDB。DolphinDB 作为一款基于高性能时序数据库…...

一天赚四五十的副业,可以试试这几种
大家都希望能够有额外的零花钱,尤其是对于学生和不收入稳定的人来说。今天,我将分享一些简单实用的赚钱技巧,帮助你每天赚取四五十的零花钱,让你的钱包更丰盈。 第一种:蚂蚁路客和友活来了 支付宝旗下两款接任务拍门…...

OpenCV 中的色彩空间 (C++ / Python)
在本教程中,我们将了解计算机视觉中使用的流行色彩空间,并将其用于基于颜色的分割。我们还将分享 C++ 和 Python 的演示代码。...

邀请函 | 高质量区块链·元宇宙—标准行系列沙龙(北京站)即将开启
区块链、元宇宙是近年来备受关注的新兴技术,也是推动数字经济发展的重要力量。高质量标准引领高质量发展,加快形成标准引领,充分释放区块链、元宇宙对实体经济牵引赋能效应,推进形成相关产业体系高质量发展新格局刻不容缓。 为进…...

php hmacsha256加密的算法
HMAC-SHA256是一种基于哈希算法的消息认证码算法,用于验证数据的完整性和真实性。它将密钥和数据一起进行哈希运算,生成一个固定长度的摘要值。只有知道密钥的人才能够验证该摘要值的真实性。 在PHP中,可以使用hash_hmac函数来计算HMAC-SHA2…...
Spring源码编译教程
1. Spring版本是5.3.10 2. 下载gradle依赖 Spring是通过gradle来编译源码下载依赖的,.gradle文件夹可以理解为gradle的仓库(和mave类似,不懂gradle的先这么理解),而我给大家的这个仓库,只包含了Spring源码…...
Python入门教程 | Python简介和环境搭建
Python 简介 Python是一种高级编程语言,由荷兰人Guido van Rossum于1991年创建。它以其简单易学、可读性强和丰富的生态系统而受到广泛喜爱。它被广泛应用于各个领域,包括Web开发、科学计算、数据分析、人工智能等。 Python的特点 简洁易读:…...
阿里云ECS服务器企业级和共享型介绍_企业级常见问题解答FAQ
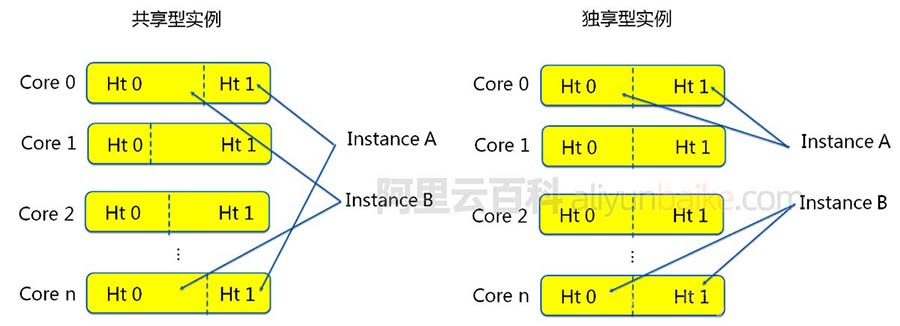
阿里云企业级服务器是什么?企业级和共享型有什么区别?企业级服务器具有独享且稳定的计算、存储、网络资源,如ECS计算型c6、通用型g8等都是企业级实例,阿里云百科分享什么是企业级云服务器、企业级实例的优势、企业级和共享型云服务…...
leetcode做题笔记92. 反转链表 II
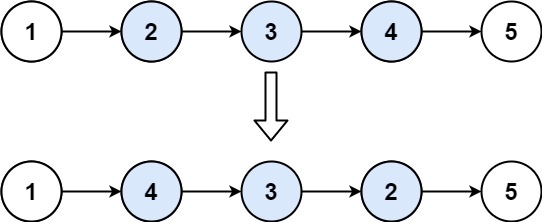
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 思路一:头插法 struct ListNode *reverseBetween(struct ListNode *h…...

springboot引入druid解析sql
一、前言 在开发中,有时我们可能会需要获取SQL中的表名,那么因为不同的数据源类型SQL会存在部分差异,那么我们就可以使用alibaba 的druid包实现不同的数据源类型的sql解析。 二、引入相关maven依赖 <dependency><groupId>com.a…...
学习笔记十九:Pod常见的状态和重启策略
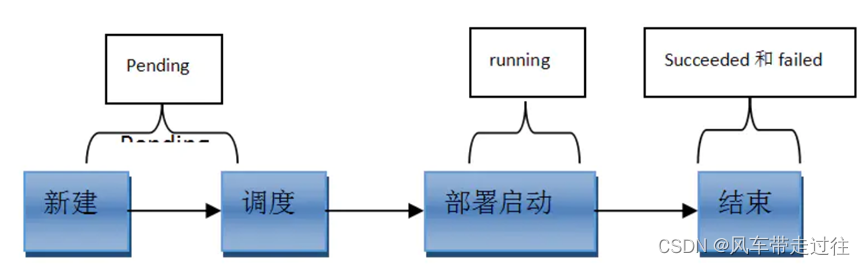
Pod常见的状态和重启策略 常见的pod状态第一阶段:第二阶段:扩展: pod重启策略测试Always重启策略正常停止容器内的tomcat服务非正常停止容器里的tomcat服务 测试never重启策略正常停止容器里的tomcat服务非正常停止容器里的tomcat服务 测试On…...

Spring的ApplicationEvent简单使用
ApplicationEvent以及Listener是Spring为我们提供的一个事件监听、订阅的实现,内部实现原理是观察者设计模式,设计初衷也是为了系统业务逻辑之间的解耦,提高可扩展性以及可维护性。事件发布者并不需要考虑谁去监听,监听具体的实现…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
