【考研数学】线形代数第三章——向量 | 基本概念、向量组的相关性与线性表示
文章目录
- 引言
- 一、向量的概念与运算
- 1.1 基本概念
- 1.2 向量运算的性质
- 二、向量组的相关性与线性表示
- 2.1 理论背景
- 2.2 相关性与线性表示基本概念
- 2.3 向量组相关性与线性表示的性质
引言
向量是线性代数的重点和难点。向量是矩阵,同时矩阵又是由向量构成的,向量组与矩阵的关系非常紧密。
一、向量的概念与运算
1.1 基本概念
向量——既有大小(长度)又有方向的量称为向量, ( a 1 , a 2 , … , a n ) T , ( a 1 , a 2 , … , a n ) (a_1,a_2,\dots,a_n)^T,(a_1,a_2,\dots,a_n) (a1,a2,…,an)T,(a1,a2,…,an) 分别称为 n n n 维列向量和 n n n 维行向量,其中 a i a_i ai 称为向量的 n n n 个分量,一般情况下我们所指的向量为列向量。
向量的模——设向量 α = ( a 1 , a 2 , … , a n ) T \alpha=(a_1,a_2,\dots,a_n)^T α=(a1,a2,…,an)T ,称 a 1 2 + a 2 2 + ⋯ + a n 2 \sqrt{a_1^2+a_2^2+\dots+a_n^2} a12+a22+⋯+an2 为向量 α \alpha α 的模或长度,记为 ∣ α ∣ . |\alpha|. ∣α∣.
向量的单位化——设向量 α = ( a 1 , a 2 , … , a n ) T \alpha=(a_1,a_2,\dots,a_n)^T α=(a1,a2,…,an)T 为非零向量,与向量 α \alpha α 方向相同且长度为 1 的向量称为 α \alpha α 对应的单位向量,令 α 0 = 1 ∣ α ∣ α , \alpha^0=\frac{1}{|\alpha|}\alpha, α0=∣α∣1α, 则称 α 0 \alpha^0 α0 为向量 α \alpha α 的单位化向量。
向量的三则运算——加、减、与一个常数相乘。
向量的内积——设向量 α = ( a 1 , a 2 , … , a n ) T \alpha=(a_1,a_2,\dots,a_n)^T α=(a1,a2,…,an)T ,设向量 β = ( b 1 , b 2 , … , b n ) T \beta=(b_1,b_2,\dots,b_n)^T β=(b1,b2,…,bn)T ,称 a 1 b 1 + a 2 b 2 + ⋯ + a n b n a_1b_1+a_2b_2+\dots+a_nb_n a1b1+a2b2+⋯+anbn 为向量 α , β \alpha ,\beta α,β 的内积,记为 ( α , β ) . (\alpha,\beta). (α,β).
1.2 向量运算的性质
(一)三则运算的性质
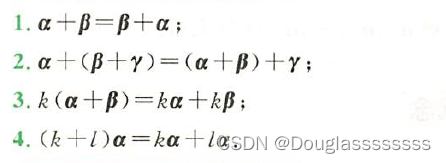
(二)向量内积运算的性质
- ( α , β ) = ( β , α ) = α T β = β T α . (\alpha,\beta)=(\beta,\alpha)=\alpha^T\beta=\beta^T\alpha. (α,β)=(β,α)=αTβ=βTα.
- ( α , α ) = α T α = ∣ α ∣ 2 , (\alpha,\alpha)=\alpha^T\alpha=|\alpha|^2, (α,α)=αTα=∣α∣2, 且 ( α , α ) = 0 (\alpha,\alpha)=0 (α,α)=0 的充要条件为 α = 0. \alpha=0. α=0.
- ( a , k 1 β 1 + k 2 β 2 + ⋯ + k n β n ) = k 1 ( α , β 1 ) + k 2 ( α 2 , β 2 ) + ⋯ + k n ( α , β n ) . (a,k_1\beta_1+k_2\beta_2+\dots+k_n\beta_n)=k_1(\alpha,\beta_1)+k_2(\alpha_2,\beta_2)+\dots+k_n(\alpha,\beta_n). (a,k1β1+k2β2+⋯+knβn)=k1(α,β1)+k2(α2,β2)+⋯+kn(α,βn).
- 若 ( α , β ) = 0 (\alpha,\beta)=0 (α,β)=0 ,即 a 1 b 1 + a 2 b 2 + ⋯ + a n b n = 0 a_1b_1+a_2b_2+\dots+a_nb_n=0 a1b1+a2b2+⋯+anbn=0 ,称 α , β \alpha,\beta α,β 正交,记为 α ⊥ β \alpha \bot \beta α⊥β ,特别地,零向量与任何向量正交。
二、向量组的相关性与线性表示
2.1 理论背景
对于齐次线性方程组:
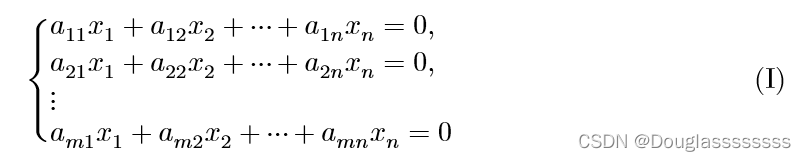
以及非齐次线性方程组:
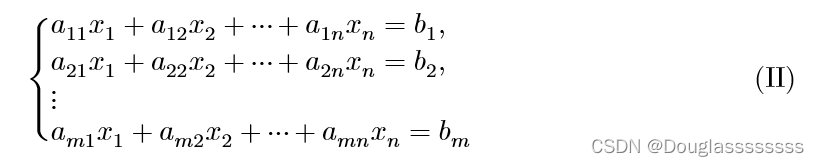
令 α 1 = ( a 11 , a 21 , … , a m 1 ) T , α 2 = ( a 12 , a 22 , … , a m 2 ) T , … , α n = ( a 1 n , a 2 n , … , a m n ) T , b = ( b 1 , b 2 , … , b m ) T \alpha_1=(a_{11},a_{21},\dots,a_{m1})^T,\alpha_2=(a_{12},a_{22},\dots,a_{m2})^T,\dots,\alpha_n=(a_{1n},a_{2n},\dots,a_{mn})^T,b=(b_{1},b_{2},\dots,b_{m})^T α1=(a11,a21,…,am1)T,α2=(a12,a22,…,am2)T,…,αn=(a1n,a2n,…,amn)T,b=(b1,b2,…,bm)T ,则方程组(I)(II)可表示为如下向量形式: x 1 α 1 + x 2 α 2 + ⋯ + x n α n = 0 ( I ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=0 (I) x1α1+x2α2+⋯+xnαn=0(I) x 1 α 1 + x 2 α 2 + ⋯ + x n α n = b ( I I ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=b (II) x1α1+x2α2+⋯+xnαn=b(II)
1,设 α 1 , α 2 , … , α n \alpha_1,\alpha_2,\dots,\alpha_n α1,α2,…,αn 为向量组,称 k 1 α 1 + k 2 α 2 + ⋯ + k n α n k_1\alpha_1+k_2\alpha_2+\dots+k_n\alpha_n k1α1+k2α2+⋯+knαn 为向量组 α 1 , α 2 , … , α n \alpha_1,\alpha_2,\dots,\alpha_n α1,α2,…,αn 的线性组合。
2,设 α 1 , α 2 , … , α n \alpha_1,\alpha_2,\dots,\alpha_n α1,α2,…,αn 为向量组, b b b 为一个向量,若存在一组数 k 1 , k 2 , … , k n k_1,k_2,\dots,k_n k1,k2,…,kn ,使得 b = k 1 α 1 + k 2 α 2 + ⋯ + k n α n b=k_1\alpha_1+k_2\alpha_2+\dots+k_n\alpha_n b=k1α1+k2α2+⋯+knαn ,称向量 b b b 可由向量组 α 1 , α 2 , … , α n \alpha_1,\alpha_2,\dots,\alpha_n α1,α2,…,αn 线性表示。
2.2 相关性与线性表示基本概念
(一)相关性
对齐次线性方程组 x 1 α 1 + x 2 α 2 + ⋯ + x n α n = 0 ( ∗ ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=0(*) x1α1+x2α2+⋯+xnαn=0(∗) (1)若方程组(*)只有零解,则向量组 α 1 , α 2 , … , α n \alpha_1,\alpha_2,\dots,\alpha_n α1,α2,…,αn 线性无关。
(2)若方程组(*)有非零解,即存在一组不全为零的数 k 1 , k 2 , … , k n k_1,k_2,\dots,k_n k1,k2,…,kn 使得 k 1 α 1 + k 2 α 2 + ⋯ + k n α n = 0 , k_1\alpha_1+k_2\alpha_2+\dots+k_n\alpha_n=0, k1α1+k2α2+⋯+knαn=0, 称向量组 α 1 , α 2 , … , α n \alpha_1,\alpha_2,\dots,\alpha_n α1,α2,…,αn 线性相关。
(二)线性表示
对非齐次线性方程组 x 1 α 1 + x 2 α 2 + ⋯ + x n α n = b ( ∗ ∗ ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=b (**) x1α1+x2α2+⋯+xnαn=b(∗∗) (1)若方程组(**)有解,即存在常数 k 1 , k 2 , … , k n k_1,k_2,\dots,k_n k1,k2,…,kn ,使得 b = k 1 α 1 + k 2 α 2 + ⋯ + k n α n b=k_1\alpha_1+k_2\alpha_2+\dots+k_n\alpha_n b=k1α1+k2α2+⋯+knαn ,称向量 b b b 可由向量组 α 1 , α 2 , … , α n \alpha_1,\alpha_2,\dots,\alpha_n α1,α2,…,αn 线性表示。
(2)若方程组(**)无解,称向量 b b b 不可由向量组 α 1 , α 2 , … , α n \alpha_1,\alpha_2,\dots,\alpha_n α1,α2,…,αn 线性表示。
2.3 向量组相关性与线性表示的性质
这一块内容多,放在下一篇文章。
相关文章:
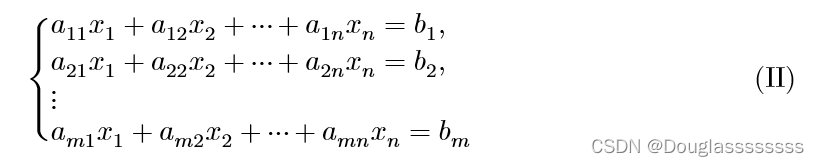
【考研数学】线形代数第三章——向量 | 基本概念、向量组的相关性与线性表示
文章目录 引言一、向量的概念与运算1.1 基本概念1.2 向量运算的性质 二、向量组的相关性与线性表示2.1 理论背景2.2 相关性与线性表示基本概念2.3 向量组相关性与线性表示的性质 引言 向量是线性代数的重点和难点。向量是矩阵,同时矩阵又是由向量构成的,…...

温故知新之:接口和抽象类有什么区别?
本文以下内容基于 JDK 8 版本。 1、接口介绍 接口是 Java 语言中的一个抽象类型,用于定义对象的公共行为。它的创建关键字是 interface,在接口的实现中可以定义方法和常量,其普通方法是不能有具体的代码实现的,而在 JDK 8 之后&…...

回归预测 | MATLAB实现SSA-RF麻雀搜索优化算法优化随机森林算法多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现SSA-RF麻雀搜索优化算法优化随机森林算法多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现SSA-RF麻雀搜索优化算法优化随机森林算法多输入单输出回归预测(多指标,多图)…...

文旅景区vr体验馆游乐场vr项目是什么
我们知道现在很多的景区或者游玩的地方,以及学校、科技馆、科普馆、商场或公园或街镇,都会建一些关于游玩以及科普学习的项目。从而增加学习氛围或者带动人流量等等。这样的形式,还是有很好的效果呈现。 普乐蛙VR体验馆案例 下面是普乐蛙做的…...
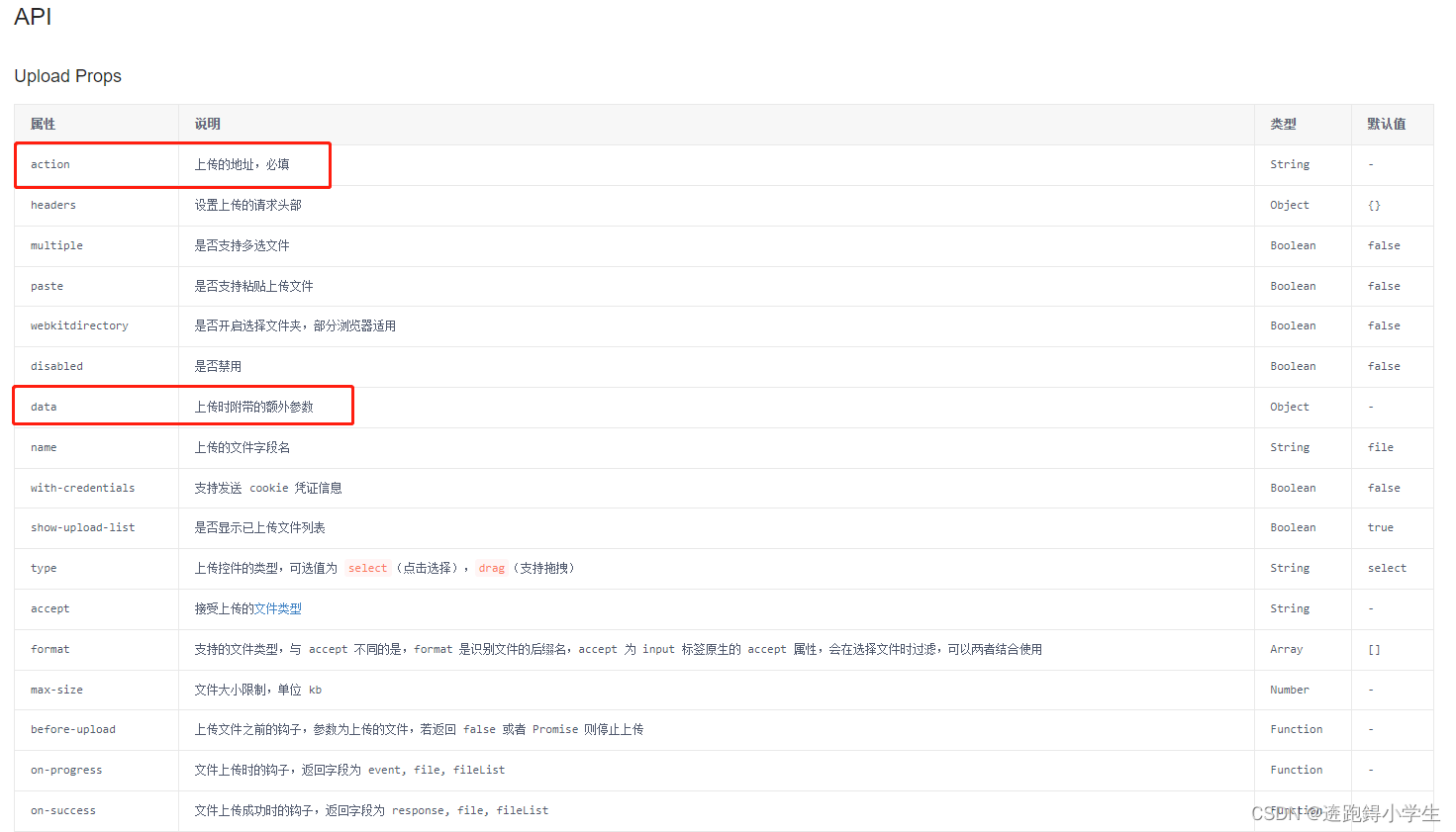
Vue Element upload组件和Iview upload 组件上传文件
今天要分享的是使用这俩个UI组件库的upload组件分别实现调用组件本身的上传方法实现和后台交互。接下来就是开车的时间,请坐稳扶好~ 一、element upload组件传送门 1、html文件 <el-upload ref"uploadRef" :action"uploadUrl" :data"…...

无涯教程-PHP - File 函数
文件系统功能用于访问和操纵文件系统,PHP为您提供了操纵文件的所有功能。 运行时配置 这些功能的行为受php.ini中的设置影响。 NameDefaultChangeableChangelogallow_url_fopen"1"PHP_INI_ALLPHP_INI_ALL in PHP < 4.3.4. PHP_INI_SYSTEM in PHP &l…...

elasticsearch 常用查询 7.4 版本
Elasticsearch 常用查询 match:全文查询exists:查询存在的字段must_not:查询不存在的字段ids:跟据id查询prefix:前缀查询range: 查询范围term:精准查询terms:多术语查询 本文基于es 7.4版本文档…...

ChatGpt 从入门到精通
相关资源下载地址: 基于ChatGPT的国际中文语法教学辅助应用的探讨.pdf 生成式人工智能技术对教育领域的影响-关于ChatGPT的专访.pdf 电子-从ChatGPT热议看大模型潜力.pdf 从图灵测试到ChatGPT——人机对话的里程碑及启示.pdf 正文 ChatGPT 是一种强大的自然语言处理模型&…...
vscode远程调试
安装ssh 在vscode扩展插件搜索remote-ssh安装 如果连接失败,出现 Resolver error: Error: XHR failedscode 报错,可以看这篇帖子vscode ssh: Resolver error: Error: XHR failedscode错误_阿伟跑呀的博客-CSDN博客 添加好后点击左上角的加号࿰…...

Vue3 数据响应式原理
核心: 通过Proxy(代理): 拦截对data任意属性的任意(13种)操作, 包括属性值的读写, 属性的添加, 属性的删除等… 通过 Reflect(反射): 动态对被代理对象的相应属性进行特定的操作 const userData {name: "John",age: 12 };let proxyUser new Proxy(use…...

2023.08.20 学习周报
文章目录 摘要文献阅读1.题目2.现有问题3.解决方案4.本文贡献5.方法5.1 利用长短期记忆网络学习时空演化特征5.2 构建用于气象辅助信息编码的堆叠自编码器5.3 使用多任务学习发现全市通用模式5.4 模型 6. 实验6.1 数据集6.2 实验设置6.3 实验结果 7.结论8.展望 大气污染物传输总…...
)
软件测试技术之单元测试—工程师 Style 的测试方法(2)
怎么写单元测试? JUnit 简介 基本上每种语言和框架都有不错的单元测试框架和工具,例如 Java 的 JUnit、Scala 的 ScalaTest、Python的 unittest、JavaScript 的 Jest 等。上面的例子都是基于 JUnit 的,我们下面就简单介绍下 JUnit。 JUnit…...

项目中超图 for openlayer和超图for cesium同时引入的问题
一个项目中同时用到了超图的openlayer和cesium版本,首先我是外部引入的超图的开发包,你要是通过npm导入的那就没关系了。 <script type"text/javascript" src"/static/openlayer/supermap/ol/iclient-ol.min.js"></script&…...
3D与沉浸式技术,如何助力企业数字化转型?
说起3D,估计许多读者朋友会在第一时间想起《阿凡达》系列和《侏罗纪公园》系列电影大作。每一帧细节纤毫毕现的逼真画面,让观众几乎分不清虚拟与现实,完全沉浸在导演打造的视觉盛宴中。 事实上,除了大家所熟知的3D影视动画之外&am…...

excel vba 将多张数据表的内容合并到一张数据表
功能描述: 一个Excel文件有很多个 样式相同 的数据表, 需要将多张数据表的内容合并到一张数据表里。 vba实现代码如下: Attribute VB_Name "NewMacros" Option Explicit Public Const Const_OutSheetName As String "V…...

接口和抽象类的区别?解析接口和抽象类的特点和用法
接口和抽象类的区别?解析接口和抽象类的特点和用法 引言 在面向对象编程中,接口和抽象类是两个非常重要的概念。它们都可以用于定义一组相关的方法,但在实际使用中有一些差异。本文将探讨接口和抽象类的区别,并通过示例代码和测…...

vscode-vue项目格式化
一、插件要求 Prettier Vetur 二、配置文件 {"workbench.startupEditor": "newUntitledFile","files.autoSave": "off", // 关闭文件自动保存,避免开发时候页面变化"editor.tabSize": 2, // tab距离"ve…...
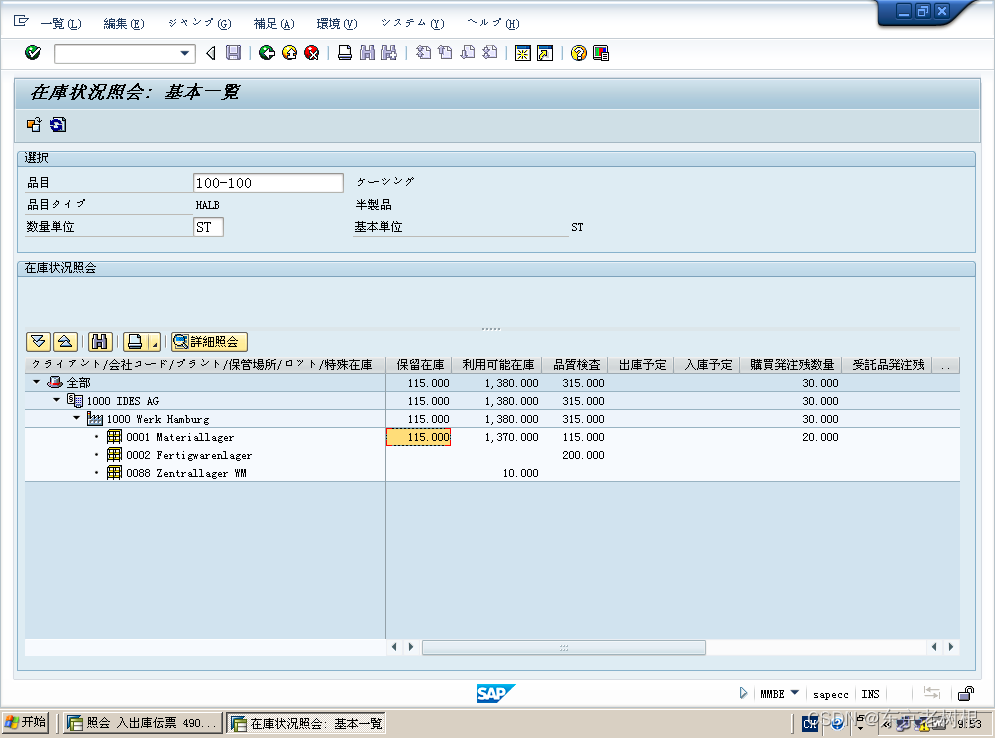
SAP MM学习笔记26- SAP中 振替转记(转移过账)和 在库转送(库存转储)1- 移动Type间振替转记
SAP 中在库移动 不仅有入库(GR),出库(GI),也可以是单纯内部的转记或转送。 1,振替转记(转移过账) 2,在库转送(库存转储) 1ÿ…...
SAP SPL(Special Ledger)之注释行项目-Noted Items
财务凭证过账里常见的SPL特殊总账标识根据业务主要有三种,BoE-billing of exchange: 汇票业务,包括商业汇票和银行汇票;Down Payment,预付款业务,包括供应商和客户预付款和申请;其它,一般是保证…...
学习平台助力职场发展与提升
近年来,随着互联网技术的发展,学习平台逐渐成为了职场发展和提升的必备工具。学习平台通过提供丰富的课程内容、灵活的学习时间和个性化的学习路径,帮助职场人士更好地提升自己的技能和知识储备,为职场发展打下坚实的基础。 学习…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
