卷积神经网络——上篇【深度学习】【PyTorch】【d2l】
文章目录
- 5、卷积神经网络
- 5.1、卷积
- 5.1.1、理论部分
- 5.1.2、代码实现
- 5.1.3、边缘检测
- 5.2、填充和步幅
- 5.2.1、理论部分
- 5.2.2、代码实现
- 5.3、多输入多输出通道
- 5.3.1、理论部分
- 5.3.2、代码实现
- 5.4、池化层 | 汇聚层
- 5.4.1、理论部分
- 5.4.2、代码实现
5、卷积神经网络
5.1、卷积
5.1.1、理论部分
全连接层后,卷积层出现的意义?
一个足够充分的照片数据集,输入,全连接层参数,GPU成本,训练时间是巨大的。
(convolutional neural networks,CNN)是机器学习利用自然图像中一些已知结构的创造性方法,需要更少的参数,在处理图像和其他类型的结构化数据上各类成本,效果,可行性普遍优于全连接层。
卷积层做了什么?
将输入和核矩阵进行互相关运算,加上偏移后得到输出。
图片中找模式的原则
- 平移不变性
- 局部性
对全连接层使用如上原则得到卷积层。
(详细待补充)
二维卷积层

Y = X ★ W + b Y = X ★ W + b Y=X★W+b
输入 X X X: n h × n w n_h × n_w nh×nw
图中,h:高、w:宽、输入大小 n = 3。
核 W W W: k h × k w k_h × k_w kh×kw
图中,卷积核大小 k = 2,超参数。
偏差 b∈ R
输出 Y Y Y: ( n h − k h + 1 ) × ( n w − k w + 1 ) ( n_h - k_h + 1)×(n_w - k_w + 1) (nh−kh+1)×(nw−kw+1)
图中 (3-2 +1)*(3-2 +1) = 4 ,计算的是 Y 的形状。
★:二维交叉操作子 | 外积
W 和 b是可学习的参数
卷积效果举例

5.1.2、代码实现
(1)实现互相关运算
卷积运算 ≠ 互相关运算
卷积运算:在卷积运算中,核心(也称为滤波器)在进行滑动时,会被翻转(180度旋转)后与输入数据进行逐元素相乘,并将乘积求和作为输出。这意味着核心的权重是翻转的。在卷积运算中,处理核心的边界像素会被覆盖,所以输出的大小通常会小于输入的大小。
互相关运算:在互相关运算中,核心与输入数据进行逐元素相乘,并将乘积求和作为输出,但核心不进行翻转。互相关运算不会覆盖核心的边界像素,所以输出的大小与输入的大小通常是一致的。
在深度学习中,人们通常使用卷积运算的术语来描述这种操作,尽管实际实现可能使用了互相关运算。卷积运算和互相关运算在数学上的操作相似,但在处理核心边界像素时存在微小的差异。在实际深度学习应用中,这两个术语通常可以互换使用。
import torch
from torch import nn
from d2l import torch as d2ldef corr2d(X, K): #@save"""计算二维互相关运算"""h, w = K.shapeY = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))for i in range(Y.shape[0]):for j in range(Y.shape[1]):#点积求和Y[i, j] = (X[i:i + h, j:j + w] * K).sum()return Y
验证运算结果
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)
result:
tensor([[19., 25.],[37., 43.]])
实现二维卷积层
class Conv2D(nn.Module):def __init__(self,kernel_size):super().__init__()self.weight =nn.Parameter(torch.rand(kernel_size))self.bias = nn.Parameter(torch.zeros(1))def forward(sekf, x):return corr2d(x,self.weight) + self.bias
(2)学习由X生成Y卷积核
#一个输入通道、一个输出通道,不使用偏置
conv2d = nn.Conv2d(1,1,kernel_size=(1,2),bias =False)X = X.reshape((1,1,6,8))
Y = Y.reshape((1,1,6,7))for i in range(10):Y_hat = conv2d(X)l = (Y_hat - Y) **2conv2d.zero_grad()l.sum().backward()conv2d.weight.data[:] -=3e-2 * conv2d.weight.gradif(i + 1)% 2 == 0:print(f'batch{i + 1}, loss {l.sum():.3f}')
所学卷积核权重
conv2d.weight.data.reshape((1,2))
tensor([[ 1.0084, -0.9816]])
5.1.3、边缘检测
利用卷积层检测 图像中的不同边缘
输入
X = torch.ones((6,8))
X[:, 2:6] =0
X
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.]])
核矩阵
K = torch.tensor([[1,-1]])
输出
Y = corr2d(X,K)
Y
tensor([[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.]])
只能检测垂直边缘
Y = corr2d(X.t(),K) Ytensor([[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.]])将核矩阵一起转置
Y = corr2d(X.t(),K.t()) Y水平边缘检测可行。
tensor([[ 0., 0., 0., 0., 0., 0.],[ 1., 1., 1., 1., 1., 1.],[ 0., 0., 0., 0., 0., 0.],[ 0., 0., 0., 0., 0., 0.],[ 0., 0., 0., 0., 0., 0.],[-1., -1., -1., -1., -1., -1.],[ 0., 0., 0., 0., 0., 0.]])
5.2、填充和步幅
5.2.1、理论部分
填充操作
更大的卷积核可以更快地减小输出大小。
如果不想结果太小,也可以通过填充实现输出更大尺寸的X,实现控制输出形状的减少量。

填充 p h p_h ph行 p w p_w pw列,输出形状:
( n h − k h + p h + 1 ) × ( n w − k w + p w + 1 ) (n_h -k_h +p_h +1)×(n_w - k_w + p_w +1) (nh−kh+ph+1)×(nw−kw+pw+1)
通常取 p h = k h − 1 , p w = k w − 1 p_h = k_h -1, \ \ \ p_w =k_w -1 ph=kh−1, pw=kw−1
- k h k_h kh奇数:上下两侧填充 p h / 2 p_h/2 ph/2
- k h k_h kh偶数:上侧填充 ⌈ p h / 2 ⌉ ⌈p_h/2⌉ ⌈ph/2⌉下侧填充 ⌊ p h / 2 ⌋ ⌊p_h/2⌋ ⌊ph/2⌋
步幅
步幅指行/列滑动步长。
设置步幅的效果?
成倍减少输出形状。
下图为高3宽2步幅示意图:

(图片来自 《DIVE INTO DEEP LEARNING》)
给定步幅,高度 s h s_h sh宽度 s w s_w sw,输出形状:
⌊ ( n h − k h + p h + s h ) / s h ⌋ × ⌊ ( n w − k w + p w + s w ) / s w ⌋ ⌊(n_h - k_h + p_h + s_h)/s_h⌋ ×⌊(n_w - k_w + p_w + s_w)/s_w⌋ ⌊(nh−kh+ph+sh)/sh⌋×⌊(nw−kw+pw+sw)/sw⌋
如果输入高度宽度可被步幅整除,形状为:
( n h / s h ) × ( n w / s w ) (n_h / s_h)×(n_w / s_w) (nh/sh)×(nw/sw)
5.2.2、代码实现
填充、步幅是卷积层超参数。
所有侧边填充一个像素
import torch
from torch import nndef comp_conv2d(conv2d, X):X = X.reshape((1,1) + X.shape)Y =conv2d(X)return Y.reshape(Y.shape[2:])conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1)
X= torch.rand(size=(8,8))
comp_conv2d(conv2d,X).shape
填充相同高度宽度
import torch
from torch import nndef comp_conv2d(conv2d, X):X = X.reshape((1,1) + X.shape)#执行一次卷积操作Y =conv2d(X)return Y.reshape(Y.shape[2:])
#padding=1 在输入数据的边界填充一行和一列的零值
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1)
X= torch.rand(size=(8,8))
comp_conv2d(conv2d,X).shape
torch.Size([8, 8])
不同高度宽度
conv2d = nn.Conv2d(1,1,kernel_size=(5,3),padding=(2,1))
comp_conv2d(conv2d,X).shape
torch.Size([8, 8])
增设步幅,其宽高为2
conv2d = nn.Conv2d(1,1,kernel_size=3,padding=1,stride =2)
comp_conv2d(conv2d,X).shape
torch.Size([4, 4])成倍缩小。
5.3、多输入多输出通道
5.3.1、理论部分
彩色RGB图片,是三通道输入数据。
每个通道都有一个卷积核,结果为各通道卷积的和。

1×1卷积层
不识别空间,用途是融合通道。
二维卷积层(多通道)
Y = X ★ W + B Y = X ★ W + B Y=X★W+B
输入 X X X: c i × n h × n w c_i × n_h × n_w ci×nh×nw
c i c_i ci输入通道数、h高、w宽、输入大小 n。
核 W W W: c o × c i × k h × k w c_o × c_i × k_h × k_w co×ci×kh×kw
c o c_o co输出通道数、卷积核大小 k。其中, c o c_o co是卷积层的超参数。
偏差 B B B : c o × c i c_o × c_i co×ci
一共有 c o × c i c_o × c_i co×ci个卷积核 每个卷积核都有一个偏差
输出 Y Y Y: c o × m h × m w c_o × m_h × m_w co×mh×mw
m h m w m_h \ m_w mh mw大小与 填充p、核大小k有关。
★:二维交叉操作子 | 外积
怎么理解每个输出通道有独立的三维卷积核?
具有三个维度:高度、宽度和通道数。
5.3.2、代码实现
(1)实现多通道互相关运算
定义多通道输入
import torch
from d2l import torch as d2l
#先遍历“X”和“K”的第0个维度(通道维度),再把它们加在一起
def corr2d_multi_in(X,K):return sum(d2l.corr2d(x,k) for x,k in zip(X,K))
多通道第零维度的几何意义?
图中X第零维度有两组,几何上就是通道数。
X :(tensor([[[0., 1., 2.],[3., 4., 5.],[6., 7., 8.]],[[1., 2., 3.],[4., 5., 6.],[7., 8., 9.]]]),
定义X,K
# X 2*3*3
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
#K 2*2*2
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])X,K,corr2d_multi_in(X, K)
(tensor([[[0., 1., 2.],[3., 4., 5.],[6., 7., 8.]],[[1., 2., 3.],[4., 5., 6.],[7., 8., 9.]]]), tensor([[[0., 1.],[2., 3.]],[[1., 2.],[3., 4.]]]), tensor([[ 56., 72.],[104., 120.]]))
定义多通道输出
def corr2d_multi_in_out(X,K):# 使用 PyTorch 的 torch.stack 函数,它将一组张量沿着指定的维度(这里是维度0)进行堆叠,生成一个新的张量。return torch.stack([corr2d_multi_in(X,k) for k in K],0)
# K+1 K的每个值加一,K规模扩成了原来3倍。
K = torch.stack((K,K+1,K+2),0)
K,K.shape
(tensor([[[[0., 1.],[2., 3.]],[[1., 2.],[3., 4.]]],[[[1., 2.],[3., 4.]],[[2., 3.],[4., 5.]]],[[[2., 3.],[4., 5.]],[[3., 4.],[5., 6.]]]]), torch.Size([3, 2, 2, 2]))返回值那一行为什么用小k对应X,多通道输入那里不是用的大K对应X,然后第零维度展开,抽出x,k对应计算吗?
K扩了三倍,所以用小k规模和原来的K相当,因此X 对应扩充前的K,扩充后的小k。
corr2d_multi_in_out(X,K)
tensor([[[ 56., 72.],[104., 120.]],[[ 76., 100.],[148., 172.]],[[ 96., 128.],[192., 224.]]])
(2)实现1*1卷积核
def corr2d_multi_in_out_1x1(X, K):c_i, h, w = X.shapec_o = K.shape[0]X = X.reshape((c_i, h * w))K = K.reshape((c_o, c_i))# 全连接层中的矩阵乘法Y = torch.matmul(K, X)return Y.reshape((c_o, h, w))
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
# 进行断言,验证使用 1x1 卷积操作得到的输出 Y1 与多通道卷积操作得到的输出 Y2 是否非常接近,以确保两种方法的结果一致
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6
5.4、池化层 | 汇聚层
5.4.1、理论部分
最大池化,每个窗口最强的模式信号,它针对卷积对空间位置敏感(边缘检测案例),允许输入有一定的偏移。
也有平均池化层。
特点
- 具有填充,步幅;
- 没有可学习的参数;
- 输出通道 = 输入通道,一一对应。
5.4.2、代码实现
池化层向前传播
import torch
from torch import nn
from d2l import torch as d2ldef pool2d(X, pool_size, mode='max'):p_h, p_w = pool_sizeY = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))for i in range(Y.shape[0]):for j in range(Y.shape[1]):if mode == 'max':Y[i, j] = X[i: i + p_h, j: j + p_w].max()elif mode == 'avg':Y[i, j] = X[i: i + p_h, j: j + p_w].mean()return Y
验证最大池化层
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]]) pool2d(X, (2, 2))tensor([[4., 5.],[7., 8.]])验证平均池化层
pool2d(X, (2,2), 'avg')tensor([[2., 3.],[5., 6.]])
使用内置的最大池化层
X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X
tensor([[[[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.],[12., 13., 14., 15.]]]])
pool2d = nn.MaxPool2d(3, padding=1, stride=2)#等价于nn.MaxPool2d((3,3), padding=(1,1), stride=(2,2))
pool2d(X)
tensor([[[[ 5., 7.],[13., 15.]]]])
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)
tensor([[[[ 5., 7.],[13., 15.]]]])
验证多通道
汇聚层在每个输入通道上单独运算,输出通道数与输入通道数相同。
拼接上
torch.cat和torch.stack的区别
torch.cat是在现有维度上进行拼接。
torch.stack用于创建一个新的维度,并将多个张量沿该新维度进行堆叠。
# 将两个张量 X, X + 1 进行拼接
X = torch.cat((X, X + 1), 1)
X
tensor([[[[ 0., 1., 2., 3.],[ 4., 5., 6., 7.],[ 8., 9., 10., 11.],[12., 13., 14., 15.]],[[ 1., 2., 3., 4.],[ 5., 6., 7., 8.],[ 9., 10., 11., 12.],[13., 14., 15., 16.]]]])
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
tensor([[[[ 5., 7.],[13., 15.]],[[ 6., 8.],[14., 16.]]]])
相关文章:

卷积神经网络——上篇【深度学习】【PyTorch】【d2l】
文章目录 5、卷积神经网络5.1、卷积5.1.1、理论部分5.1.2、代码实现5.1.3、边缘检测 5.2、填充和步幅5.2.1、理论部分5.2.2、代码实现 5.3、多输入多输出通道5.3.1、理论部分5.3.2、代码实现 5.4、池化层 | 汇聚层5.4.1、理论部分5.4.2、代码实现 5、卷积神经网络 5.1、卷积 …...

【从零学习python 】54. 内存中写入数据
文章目录 内存中写入数据StringIOBytesIO进阶案例 内存中写入数据 除了将数据写入到一个文件以外,我们还可以使用代码,将数据暂时写入到内存里,可以理解为数据缓冲区。Python中提供了StringIO和BytesIO这两个类将字符串数据和二进制数据写入…...
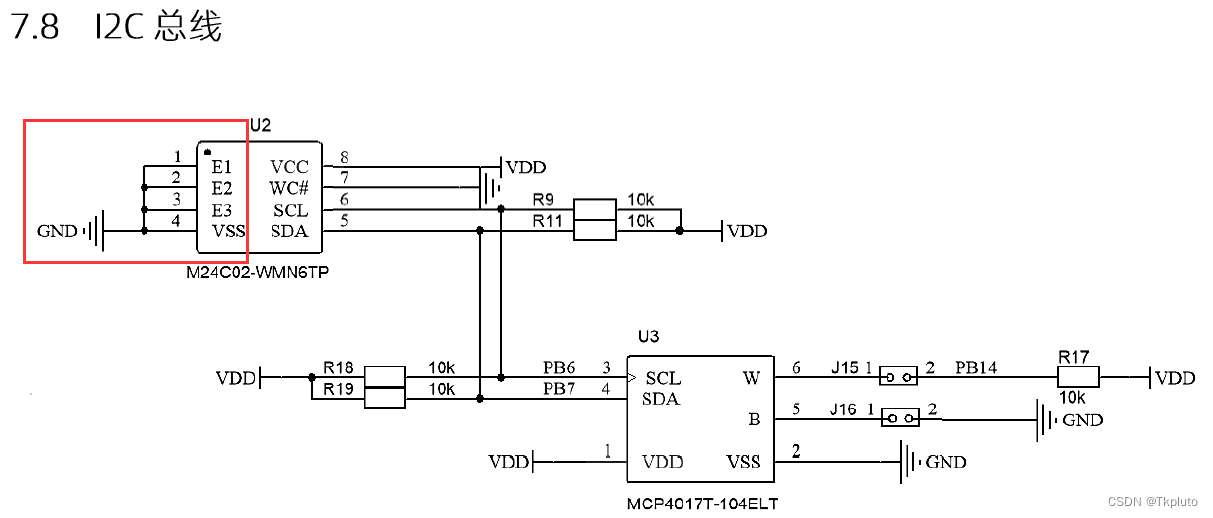
速通蓝桥杯嵌入式省一教程:(九)AT24C02芯片(E2PROM存储器)读写操作与I2C协议
AT24C02芯片(又叫E2PROM存储器、EEPROM存储器),是一种通过I2C(IIC)协议通信的掉电保存存储器芯片,其内部含有256个8位字节。在介绍这款芯片之前,我们先来粗略了解一下I2C协议。 I2C总线是一种双向二线制的同步串行总线…...

负载均衡:优化性能与可靠性的关键
在现代互联网时代,数以万计的用户访问着各种在线服务,从即时通讯、社交媒体到电子商务和媒体流媒体,无不需要应对海量的请求和数据传输。在这个高并发的环境下,负载均衡成为了关键的技术,它旨在分散工作负载࿰…...

T113-S3-TCA6424-gpio扩展芯片调试
目录 前言 一、TCA6424介绍 二、原理图连接 三、设备树配置 四、内核配置 五、gpio操作 总结 前言 TCA6424是一款常用的GPIO(通用输入输出)扩展芯片,可以扩展微控制器的IO口数量。在T113-S3平台上,使用TCA6424作为GPIO扩展芯…...

奥威BI数据可视化工具:个性化定制,打造独特大屏
每个人都有自己独特的审美,因此即使是做可视化大屏,也有很多人希望做出不一样的报表,用以缓解审美疲劳的同时提高报表浏览效率。因此这也催生出了数据可视化工具的个性化可视化大屏制作需求。 奥威BI数据可视化工具:个性化定制&a…...

13 秒插入 30 万条数据,批量插入!
数据库表 CREATE TABLE t_user (id int(11) NOT NULL AUTO_INCREMENT COMMENT 用户id,username varchar(64) DEFAULT NULL COMMENT 用户名称,age int(4) DEFAULT NULL COMMENT 年龄,PRIMARY KEY (id) ) ENGINEInnoDB DEFAULT CHARSETutf8 COMMENT用户信息表; User实体 /*** …...
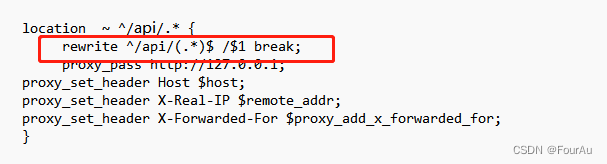
Nginx代理转发地址不正确问题
使用ngix前缀去代理转发一个地址,貌似成功了,但是进不到正确的页面,能够访问,但是一直404远处出来nginx会自动拼接地址在后面 后面才知道要将这段代码加上去,去除前缀转发...

HyperMotion高度自动化云迁移至华为HCS8.1解决方案
项目背景 2020 年以来,金融证券已经成为信创落地最快的领域。2021 年证监会发布的《证券期货业科技发展十四五规划》中,将“加强信创规划与实施”作为证券行业重点建设任务之一。为了符合国家信创标准,某证券企业计划将网管系统、呼叫中心管…...

pbootcms系统安全防护设置大全
PbootCMS系统简介 PbootCMS是全新内核且永久开源免费的PHP企业网站开发建设管理系统,是一套高效、简洁、 强悍的可免费商用的PHP CMS源码,能够满足各类企业网站开发建设的需要。系统采用简单到想哭的模板标签,只要懂HTML就可快速开发企业网站…...

【环境】docker时间与宿主同步
1.容器创建后 docker cp /etc/localtime 容器名:/etc/2.容器创建时 加入 -v /ect/localtime/:/etc/localtime:ro参考链接...
亮点!视频云存储/安防监控视频智能分析平台睡岗离岗检测
在生产过程中,未经领导允许的擅自离岗、睡岗会带来很多的潜在危害。TSINGSEE青犀推出的视频云存储/安防监控视频智能分析平台得睡岗离岗检测根据AI视频分析技术建立人工智能算法,对视频画面展开分析与识别。自动识别出人员睡岗、离岗、玩手机与抽烟等动作…...

编程锦囊妙计——快速创建本地Mock服务
点击上方👆蓝色“Agilean”,发现更多精彩。 前情提要 在本系列上一篇文章《全文干货:打破前后端数据传递鸿沟,高效联调秘笈》中我们分享了使用Zod这一运行时类型校验库来对后端服务响应结果进行验证达到增加项目质量的方式。 这次…...

简单认识镜像底层原理详解和基于Docker file创建镜像
文章目录 一、镜像底层原理1.联合文件系统(UnionFS)2.镜像加载原理3.为什么Docker里的centos的大小才200M? 二、Dockerfile1.简介2.Dockerfile操作常用命令 三、创建Docker镜像1.基于已有镜像创建2.基于本地模板创建3.基于Dockerfile创建4.Dockerfile多阶段构建镜像 一、镜像底…...

加速乐(__jsl_clearance_s)动态cookie生成分析实战
文章目录 一、写在前面二、抓包分析三、逆向分析 一、写在前面 加速乐(JSL)是阿里推出的一项反爬虫服务,其生成cookie的原理基于浏览器的行为特征 我们知道普通网站生成cookie是在请求时生成,而它先生成cookie,然后向服…...

启动Vue项目踩坑记录
前言 在启动自己的Vue项目时,遇到一些报错,当时很懵,解决了以后豁然开朗,特写此博客记录一下。 一、<template>里多加了个div标签 [vite] Internal server error: At least one <template> or <script> is req…...

vue-pc上传优化-uni-app上传优化
vue-pc上传优化 当我们使用自己搭建的文档服务器上传图片时候,在本地没问题,上线上传会比较慢 这时候我们最简单的方法就是写一个加载组件,上传之前打开组件,掉完接口关闭组件 或者不想写直接使用element的loading写一个遮罩层加…...

【计算机视觉|生成对抗】StackGAN:使用堆叠生成对抗网络进行文本到照片逼真图像合成
本系列博文为深度学习/计算机视觉论文笔记,转载请注明出处 标题:StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks 链接:[1612.03242] StackGAN: Text to Photo-realistic Image Synthesis…...

跟随角色镜头时,解决地图黑线/白线缝隙的三种方案
下面一共三个解决方案,这里我推荐第二个方案解决,因为够快速和简单。 现象: 解决方案一: 参考【Unity2D】去除地图中的黑线_unity选中后有线_香菇CST的博客-CSDN博客,博主解释是因为抗锯齿采样导致的问题。 具体到这…...
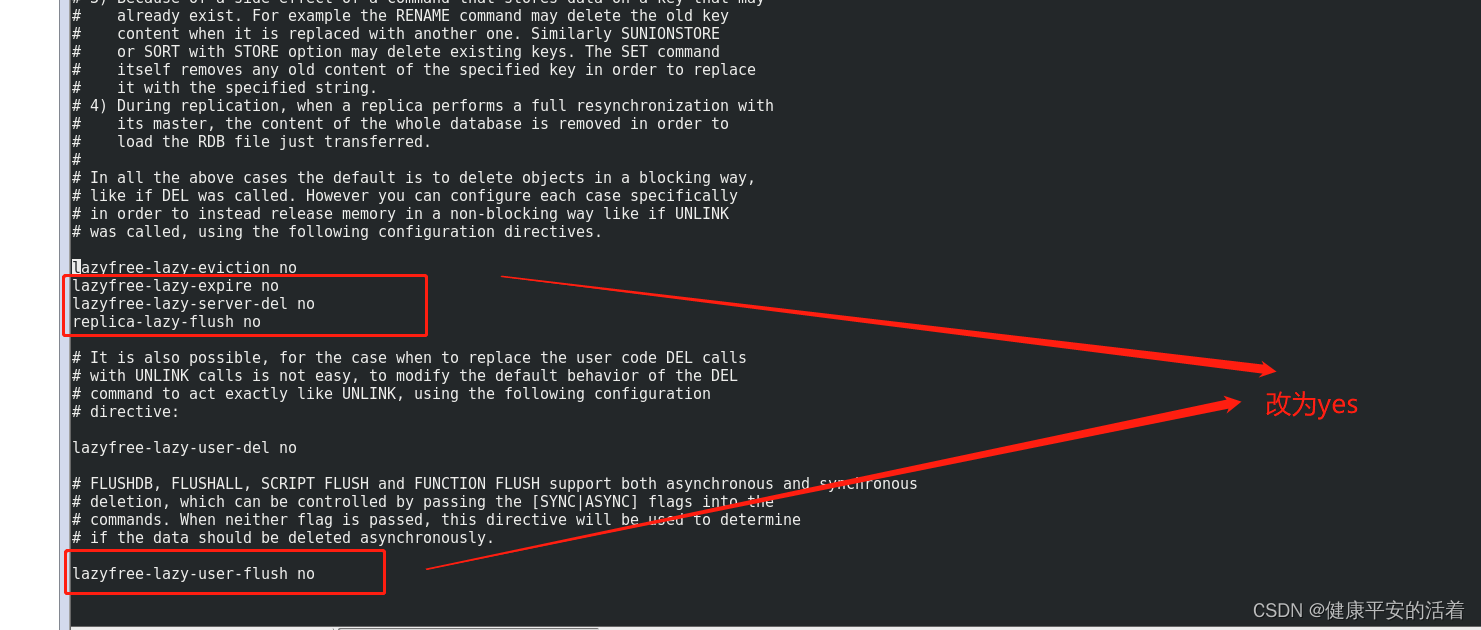
redis7高级篇2 redis的BigKey的处理
一 Bigkey的处理 1.1 模拟造数 1.截图 2.代码 :使用pipe 批量插入10w的数据量 cat /root/export/monidata.txt | redis-cli -h 127.0.0.1 -a 123456 -p 6379 --pipe [rootlocalhost export]# for((i1;i<10*10;i)); do echo "set k$i v$i" >>…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
