USACO18DEC Fine Dining G
P5122 [USACO18DEC] Fine Dining G
题目大意
有一个由 n n n个点 m m m条边构成的无向连通图,这 n n n个点的编号为 1 1 1到 n n n。前 n − 1 n-1 n−1个点上都有一头奶牛,这些奶牛都要前往 n n n号点。第 i i i条边连接 a i a_i ai和 b i b_i bi,经过需要时间 t i t_i ti。
有 k k k个干草捆分布在这些点中,第 i i i个干草捆的美味值为 y i y_i yi。每头奶牛都希望能够在某一处干草捆处停留并吃草,但奶牛只会在经过这个干草捆使她回牛棚的时间增加不超过这个干草捆的美味值时这样做。一头奶牛只会在一处干草捆处停留并吃草。
输出有 n − 1 n-1 n−1行。如果第 i i i个点的奶牛可以在回牛棚的路上会前往某一个干草捆并且在此进食,则第 i i i行输出 1 1 1;否则,输出 0 0 0。
可能有多个干草捆在同一个点。
2 ≤ n ≤ 5 × 1 0 4 , 1 ≤ m ≤ 1 0 5 2\leq n\leq5\times 10^4,1\leq m\leq 10^5 2≤n≤5×104,1≤m≤105
题解
用 dijkstra \text{dijkstra} dijkstra算出第 n n n个点到各个点的距离,设到第 i i i个点的距离为 d i s i dis_i disi。
将所有有干草捆的点 x x x作为第二次 dijkstra \text{dijkstra} dijkstra的起点,起始值设为 d i s x − y x dis_x-y_x disx−yx,意为从点 x x x到点 n n n的距离减去这个干草捆的美味值。用这些点为起点做一次 dijkstra \text{dijkstra} dijkstra,到各个点的距离记为 t d i td_i tdi。
最后,对于每个 1 ≤ i < n 1\leq i<n 1≤i<n,如果 t d i ≤ d i s i td_i\leq dis_i tdi≤disi,则可以在一个干草捆停留,否则不行。
时间复杂度为 O ( ( n + m ) log n ) O((n+m)\log n) O((n+m)logn)。
code
#include<bits/stdc++.h>
using namespace std;
int n,m,k,x,y,z,tot=0,d[200005],l[200005],r[200005],w[200005];
int vs[100005],dis[100005],td[100005];
struct node{int id,x;bool operator<(const node ax)const{return x>ax.x;}
};
priority_queue<node>q;
void add(int xx,int yy,int zz){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;w[tot]=zz;
}
void dd1(){for(int i=1;i<=n;i++){vs[i]=0;dis[i]=2e9;}dis[n]=0;q.push((node){n,0});while(!q.empty()){int u=q.top().id;q.pop();if(vs[u]) continue;vs[u]=1;for(int i=r[u];i;i=l[i]){if(dis[d[i]]>dis[u]+w[i]){dis[d[i]]=dis[u]+w[i];q.push((node){d[i],dis[d[i]]});}}}
}
void dd2(){for(int i=1;i<=n;i++){vs[i]=0;if(td[i]<2e9) q.push((node){i,td[i]});}while(!q.empty()){int u=q.top().id;q.pop();if(vs[u]) continue;vs[u]=1;for(int i=r[u];i;i=l[i]){if(td[d[i]]>td[u]+w[i]){td[d[i]]=td[u]+w[i];q.push((node){d[i],td[d[i]]});}}}
}
int main()
{scanf("%d%d%d",&n,&m,&k);for(int i=1;i<=m;i++){scanf("%d%d%d",&x,&y,&z);add(x,y,z);add(y,x,z);}dd1();for(int i=1;i<=n;i++) td[i]=2e9;for(int i=1;i<=k;i++){scanf("%d%d",&x,&z);td[x]=min(td[x],dis[x]-z);}dd2();for(int i=1;i<n;i++){if(td[i]<=dis[i]) printf("1\n");else printf("0\n");}return 0;
}
相关文章:

USACO18DEC Fine Dining G
P5122 [USACO18DEC] Fine Dining G 题目大意 有一个由 n n n个点 m m m条边构成的无向连通图,这 n n n个点的编号为 1 1 1到 n n n。前 n − 1 n-1 n−1个点上都有一头奶牛,这些奶牛都要前往 n n n号点。第 i i i条边连接 a i a_i ai和 b i b_i bi…...

fckeditor编辑器的两种使用方法
需要的资源包我放我资源里了,不要积分 https://download.csdn.net/download/wybshyy/88245895 首先把FredCK.FCKeditorV2.dll添加到引用 具体方法如下,一个是客户端版本,一个是服务器端版本 客户端版本: <% Page Language…...
)
数据结构,查找算法(二分,分块,哈希)
一、查找算法 1、二分查找:(前提条件: 必须有序的序列) #include <stdio.h> //二分查找 value代表的是被查找的值 int findByHalf(int *p, int n, int value) {int low = 0;//low低int high = n-1;//high高int middle;//用来保存中间位置的下标while(low <= high…...

C++(Qt)软件调试---gdb调试入门用法(12)
gdb调试—入门用法(1) 文章目录 gdb调试---入门用法(1)1、前言1.1 什么是GDB1.2 为什么要学习GDB1.3 主要内容1.4 GDB资料 2、C/C开发调试环境准备3、gdb启动调试1.1 启动调试并传入参数1.2 附加到进程1.3 过程执行1.4 退出调试 4…...
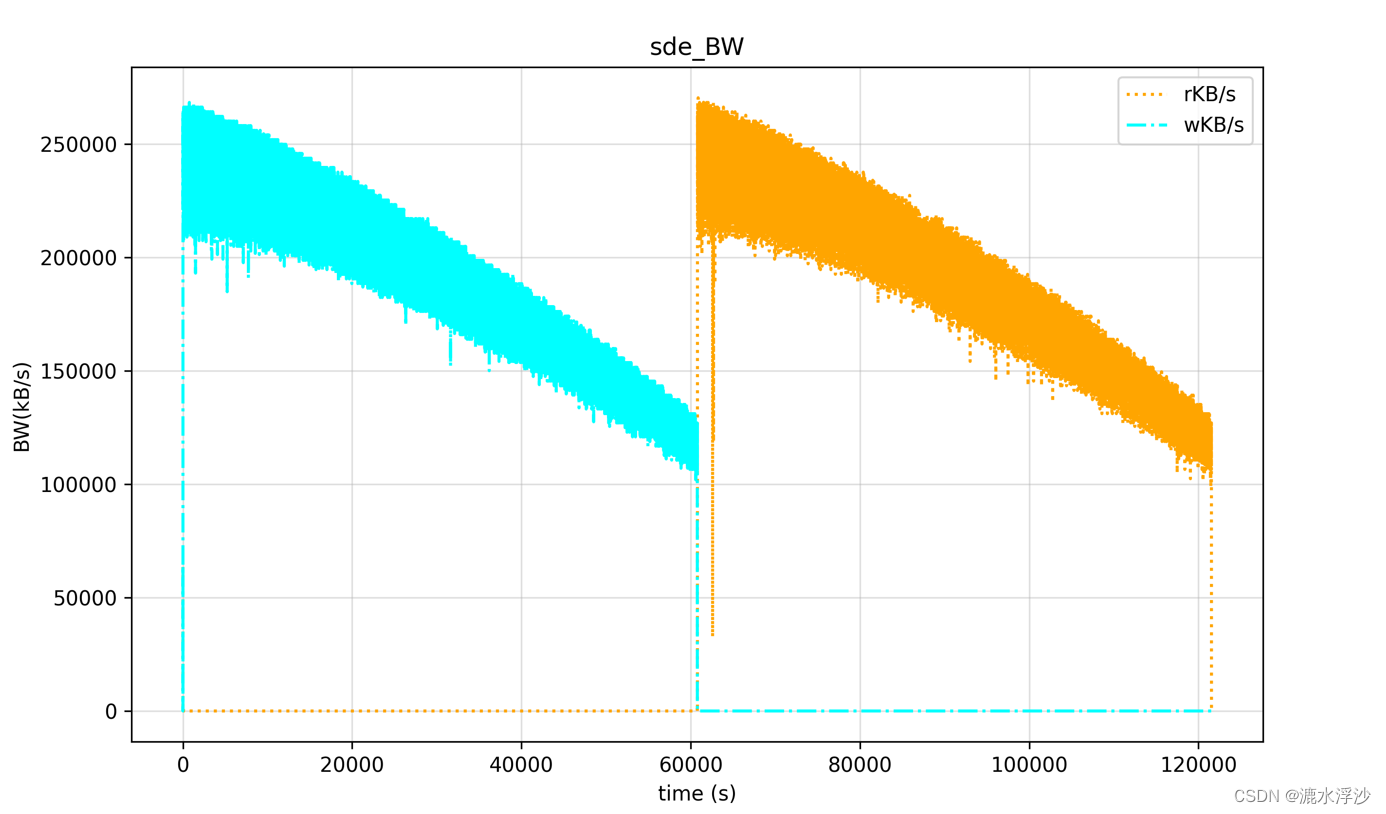
shell和Python 两种方法分别画 iostat的监控图
在服务器存储的测试中,经常需要看performance的性能曲线,这样最能直接观察HDD或者SSD的性能曲线。 如下这是一个针对HDD跑Fio读写的iostat监控log,下面介绍一下分别用shell 和Python3 写画iostat图的方法 1 shell脚本 环境:linux OS gnuplot工具 第一步 :解析iosta…...
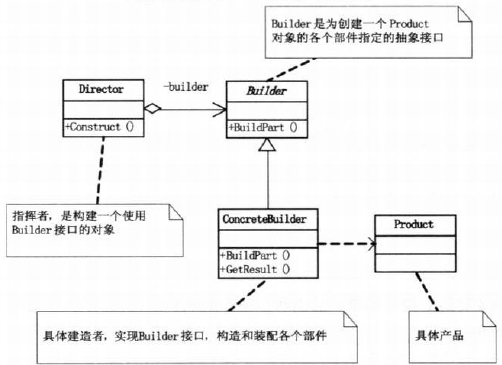
设计模式(9)建造者模式
一、 1、概念:将一个复杂对象的构造与它的表示分离,使得同样的构造过程可以创建不同的表示。建造者模式主要用于创建一些复杂的对象,这些对象内部构建间的顺序通常是稳定的,但对象内部的构建通常面临着复杂的变化;建造…...
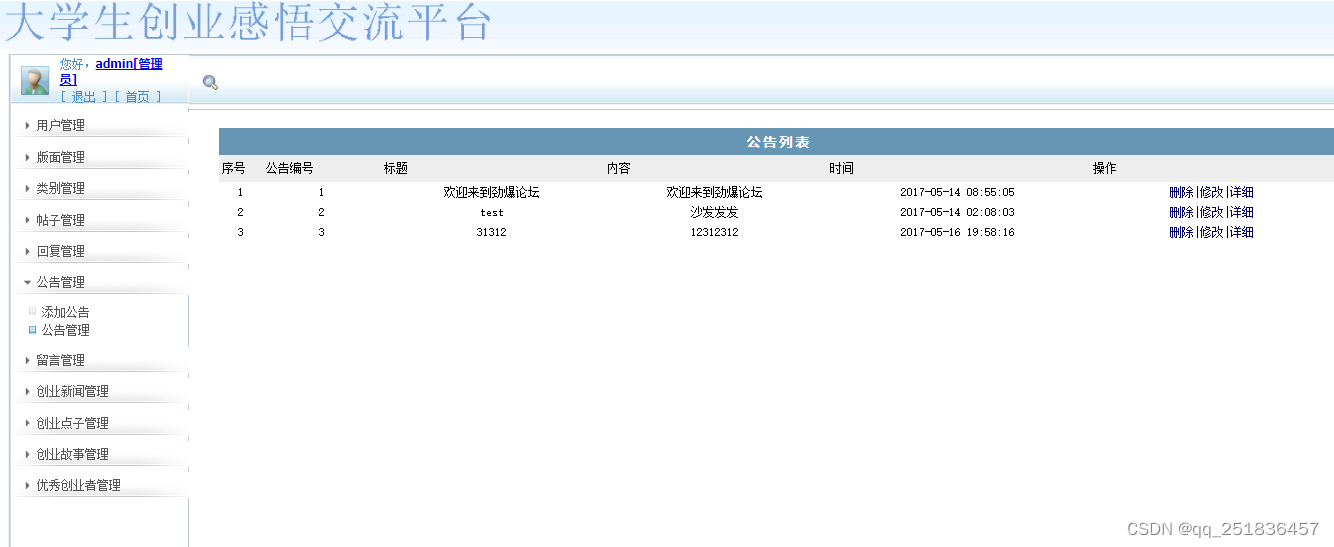
PHP 创业感悟交流平台系统mysql数据库web结构apache计算机软件工程网页wamp
一、源码特点 PHP 创业感悟交流平台系统(含论坛)是一套完善的web设计系统,对理解php编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 源码下载: https://download.csdn.…...
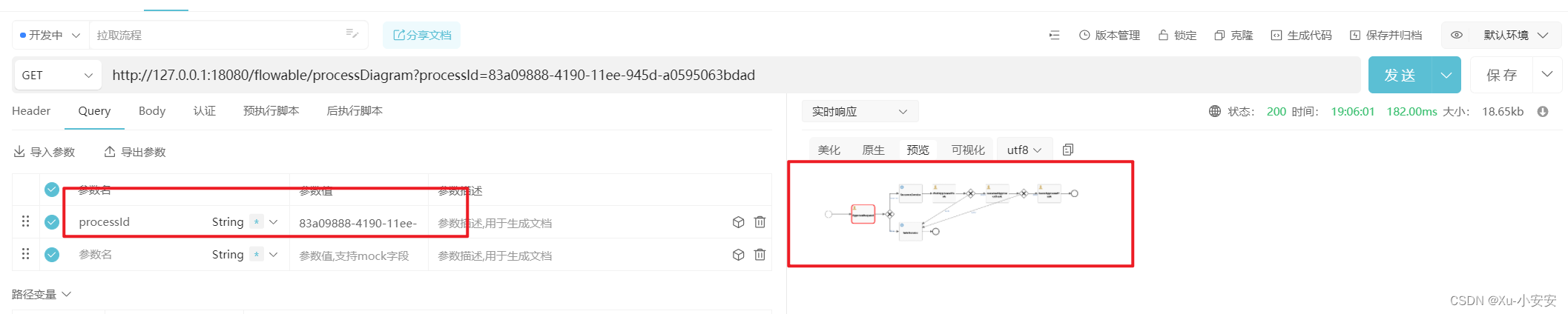
工作流程引擎之flowable(集成springboot)
0、背景 现状:公司各部门业务系统有各自的工作流引擎,也有cross function的业务在不同系统或OA系统流转,没有统一的去规划布局统一的BPM解决方案,近期由于一个项目引发朝着整合统一的BPM方案,特了解一下市面上比较主流…...

leetcode54. 螺旋矩阵(java)
螺旋矩阵 题目描述解题 收缩法 上期经典算法 题目描述 难度 - 中等 原题链接 - leecode 54 螺旋矩阵 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例1: 输入:matrix [[1,2,3],[4,5,6],[7…...

go gorm 查询
定义model package mysqltestimport ("errors""fmt""gorm.io/gorm" )type Product struct {gorm.ModelID uint gorm:"primarykey"Name string gorm:"column:name"Price float64 gorm:"column:price_value&quo…...

Flutter GetXController 动态Tabbar 报错问题
场景: 1.Tabbar的内容是接口获取的 2. TabController? tabController;; 在onInit 方法中初始化tabbarController tabController TabController(initialIndex: 0, length: titleDataList.length, vsync: this); 这时候会报一个错误 Controllers l…...
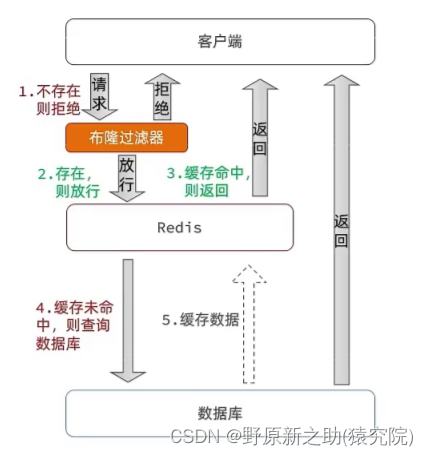
Redis(缓存预热,缓存雪崩,缓存击穿,缓存穿透)
目录 一、缓存预热 二、缓存雪崩 三、缓存击穿 四、缓存穿透 一、缓存预热 开过车的都知道,冬天的时候启动我们的小汽车之后不要直接驾驶,先让车子发动机预热一段时间再启动。缓存预热是一样的道理。 缓存预热就是系统启动前,提前将相关的…...
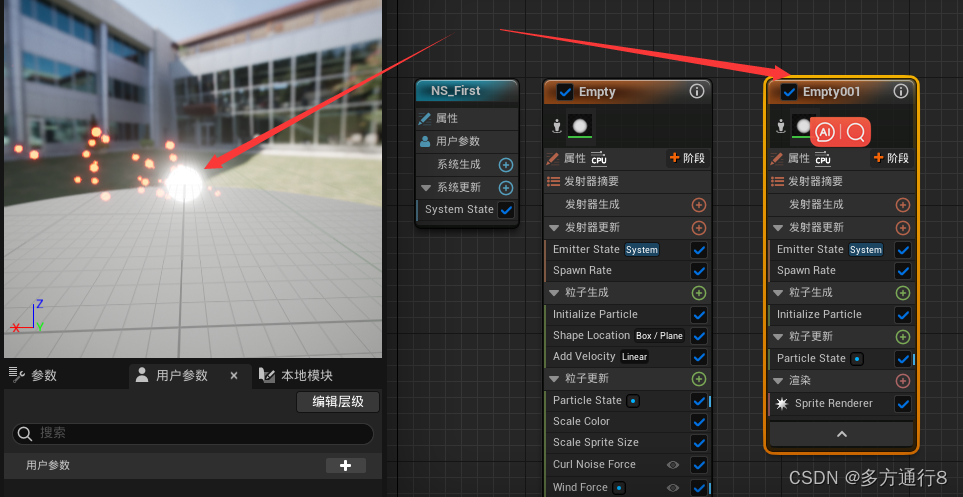
UE4/5Niagara粒子特效学习(使用UE5.1,适合新手)
目录 创建空模板 创建粒子 粒子的基础属性 粒子的生命周期 颜色 大小设置 生成的位置 Skeletal Mesh Location的效果: Shape Location 添加速度 添加Noise力场 在生成中添加: 效果: 编辑 在更新中添加: 效果&…...

from moduleA import * 语句 和import moduleA 的区别
from moduleA import * 语句和import moduleA 的区别是: from moduleA import * 语句会将moduleA模块中的所有内容(函数、变量、类等)直接导入到当前模块的命名空间中,这样就可以直接使用它们,而不需要加上模块名的限…...
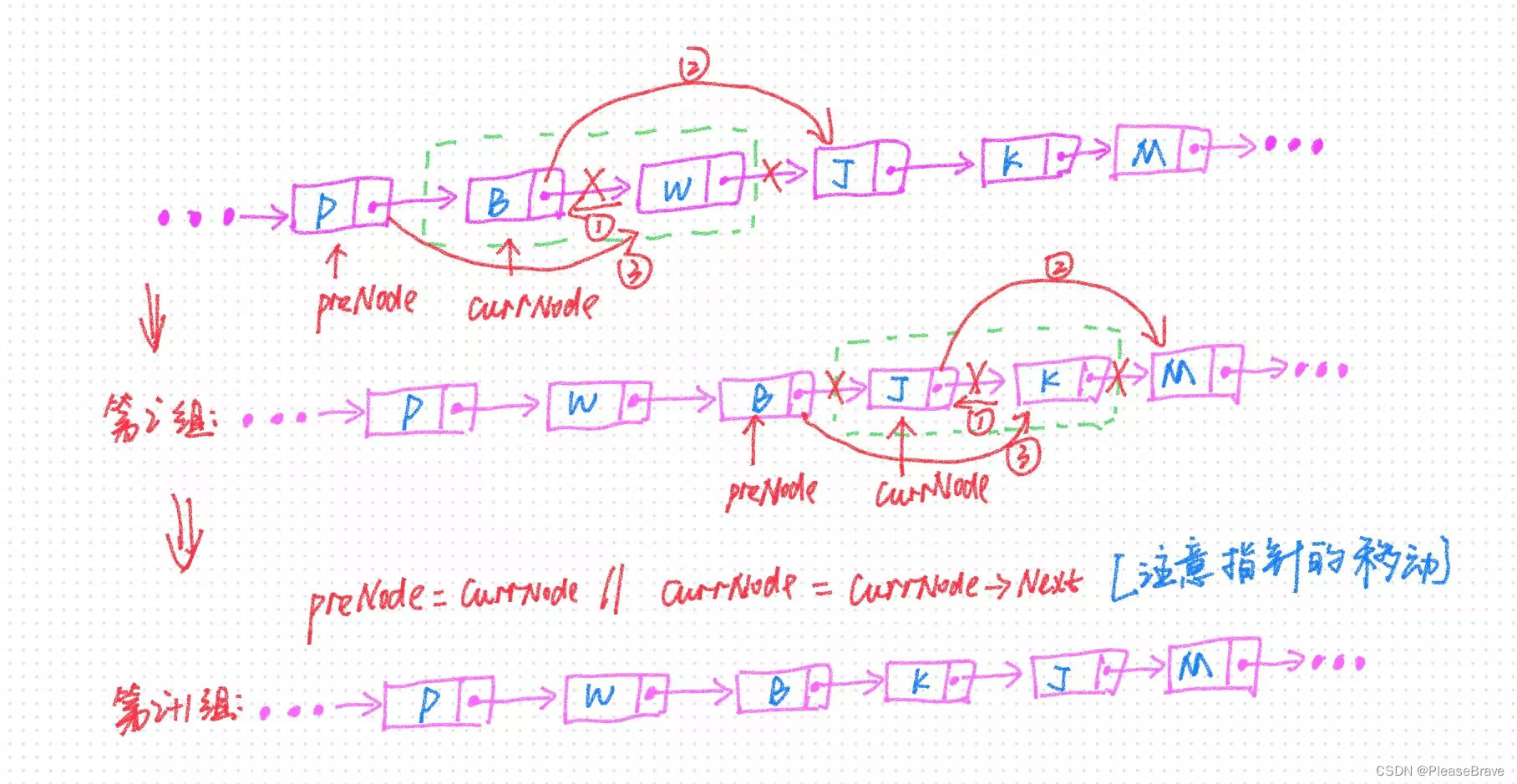
【leetcode 力扣刷题】交换链表中的节点
24. 两两交换链表中的节点 24. 两两交换链表中的节点两两节点分组,反转两个节点连接递归求解 24. 两两交换链表中的节点 题目链接:24. 两两交换链表中的节点 题目内容: 题目中强调不能修改节点内部值,是因为如果不加这个限制的话…...

学会Mybatis框架:让你的代码更具灵活性、可维护性、安全性和高效性【二.动态SQL】
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于Mybatis的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.Mybatis动态SQL如何应用 1.需求 2.…...

Oracle 中 ROWNUM 使用问题记录
ROWNUM 使用问题记录(2023-08-17) Oracle 版本: 19.0.0.0.0 Enterprise现象:今天在项目遇到一个问题,测试人员反馈前一天能看到的数据今天看不到了 用表格举例,这是前一天看到的数据,有9、7、1 这几个数量信息 日期…...
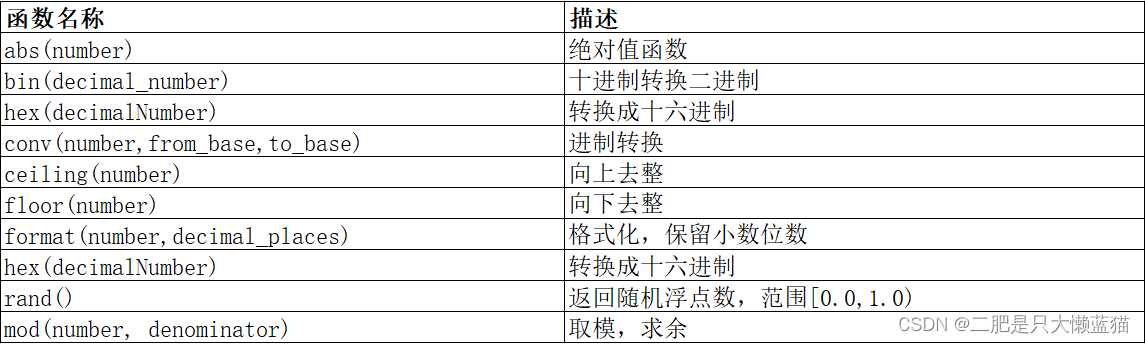
MySQL数据库:内置函数
日期函数 规定:日期:年月日 时间:时分秒 函数名称作用描述current_date()当前日期current_time()当前时间current_timestamp()当前时间戳date(datetime)返回datetime参数的日期部分date_add(date,interval d_value_type)在date中添加…...

【C++杂货铺】探索string的底层实现
文章目录 一、成员变量二、成员函数2.1 默认构造函数2.2 拷贝构造函数2.3 operator2.4 c_str()2.5 size()2.6 operator[ ]2.7 iterator2.8 reserve2.9 resize2.10 push_back2.11 append2.12 operator2.13 insert2.14 erase2.15 find2.16 substr2.17 operator<<2.18 opera…...
c++ day1
定义一个命名空间Myspace,包含以下函数:将一个字符串中的所有单词进行反转,并输出反转后的结果。例如,输入字符串为"Hello World",输出结果为"olleH dlroW",并在主函数内测试该函数。 …...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
