排序算法:选择排序
选择排序的思想是:双重循环遍历数组,每经过一轮比较,找到最小元素的下标,将其交换至首位。
public static void selectionSort(int[] arr) {int minIndex;for (int i = 0; i < arr.length - 1; i++) {minIndex = i;for (int j = i + 1; j < arr.length; j++) {if (arr[minIndex] > arr[j]) {// 记录最小值的下标minIndex = j;}}// 将最小元素交换至首位int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}
}选择排序就好比第一个数字站在擂台上,大吼一声:“还有谁比我小?”。剩余数字来挨个打擂,如果出现比第一个数字小的数,则新的擂主产生。每轮打擂结束都会找出一个最小的数,将其交换至首位。经过 n-1 轮打擂,所有的数字就按照从小到大排序完成了。
现在让我们思考一下,冒泡排序和选择排序有什么异同?
相同点:
- 都是两层循环,时间复杂度都为 O(n²);
- 都只使用有限个变量,空间复杂度 O(1);
不同点:
- 冒泡排序在比较过程中就不断交换;而选择排序增加了一个变量保存最小值 / 最大值的下标,遍历完成后才交换,减少了交换次数。
事实上,冒泡排序和选择排序还有一个非常重要的不同点,那就是:
- 冒泡排序法是稳定的,选择排序法是不稳定的。
想要理解这点不同,我们先要知道什么是排序算法的稳定性。
排序算法的稳定性
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且 r[i] 在 r[j] 之前,而在排序后的序列中,r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
理解了稳定性的定义后,我们就能分析出:冒泡排序中,只有左边的数字大于右边的数字时才会发生交换,相等的数字之间不会发生交换,所以它是稳定的。
而选择排序中,最小值和首位交换的过程可能会破坏稳定性。比如数列:[2, 2, 1],在选择排序中第一次进行交换时,原数列中的两个 2 的相对顺序就被改变了,因此,我们说选择排序是不稳定的。
那么排序算法的稳定性有什么意义呢?其实它只在一种情况下有意义:当要排序的内容是一个对象的多个属性,且其原本的顺序存在意义时,如果我们需要在二次排序后保持原有排序的意义,就需要使用到稳定性的算法。
举个例子,如果我们要对一组商品排序,商品存在两个属性:价格和销量。当我们按照价格从高到低排序后,要再按照销量对其排序,这时,如果要保证销量相同的商品仍保持价格从高到低的顺序,就必须使用稳定性算法。
当然,算法的稳定性与具体的实现有关。在修改比较的条件后,稳定性排序算法可能会变成不稳定的。如冒泡算法中,如果将「左边的数大于右边的数,则交换」这个条件修改为「左边的数大于或等于右边的数,则交换」,冒泡算法就变得不稳定了。
同样地,不稳定排序算法也可以经过修改,达到稳定的效果。思考一下,选择排序算法如何实现稳定排序呢?
实现的方式有很多种,这里给出一种最简单的思路:新开一个数组,将每轮找出的最小值依次添加到新数组中,选择排序算法就变成稳定的了。
但如果将寻找最小值的比较条件由arr[minIndex] > arr[j]修改为arr[minIndex] >= arr[j],即使新开一个数组,选择排序算法依旧是不稳定的。所以分析算法的稳定性时,需要结合具体的实现逻辑才能得出结论,我们通常所说的算法稳定性是基于一般实现而言的。
二元选择排序
选择排序算法也是可以优化的,既然每轮遍历时找出了最小值,何不把最大值也顺便找出来呢?这就是二元选择排序的思想。
使用二元选择排序,每轮选择时记录最小值和最大值,可以把数组需要遍历的范围缩小一倍。
public static void selectionSort2(int[] arr) {int minIndex, maxIndex;// i 只需要遍历一半for (int i = 0; i < arr.length / 2; i++) {minIndex = i;maxIndex = i;for (int j = i + 1; j < arr.length - i; j++) {if (arr[minIndex] > arr[j]) {// 记录最小值的下标minIndex = j;}if (arr[maxIndex] < arr[j]) {// 记录最大值的下标maxIndex = j;}}// 如果 minIndex 和 maxIndex 都相等,那么他们必定都等于 i,且后面的所有数字都与 arr[i] 相等,此时已经排序完成if (minIndex == maxIndex) break;// 将最小元素交换至首位int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;// 如果最大值的下标刚好是 i,由于 arr[i] 和 arr[minIndex] 已经交换了,所以这里要更新 maxIndex 的值。if (maxIndex == i) maxIndex = minIndex;// 将最大元素交换至末尾int lastIndex = arr.length - 1 - i;temp = arr[lastIndex];arr[lastIndex] = arr[maxIndex];arr[maxIndex] = temp;}
}我们使用 minIndex 记录最小值的下标,maxIndex 记录最大值的下标。每次遍历后,将最小值交换到首位,最大值交换到末尾,就完成了排序。
由于每一轮遍历可以排好两个数字,所以最外层的遍历只需遍历一半即可。
二元选择排序中有一句很重要的代码,它位于交换最小值和交换最大值的代码中间:
if (maxIndex == i) maxIndex = minIndex;这行代码的作用处理了一种特殊情况:如果最大值的下标等于 i,也就是说 arr[i] 就是最大值,由于 arr[i] 是当前遍历轮次的首位,它已经和 arr[minIndex] 交换了,所以最大值的下标需要跟踪到 arr[i] 最新的下标 minIndex。
二元选择排序的效率
在二元选择排序算法中,数组需要遍历的范围缩小了一倍。那么这样可以使选择排序的效率提升一倍吗?
从代码可以看出,虽然二元选择排序最外层的遍历范围缩小了,但 for 循环内做的事情翻了一倍。也就是说二元选择排序无法将选择排序的效率提升一倍。但实测会发现二元选择排序的速度确实比选择排序的速度快一点点,它的速度提升主要是因为两点:
- 在选择排序的外层 for 循环中,i 需要加到 arr.length - 1 ,二元选择排序中 i 只需要加到 arr.length / 2;
- 在选择排序的内层 for 循环中,j 需要加到 arr.length ,二元选择排序中 j 只需要加到 arr.length - i;
我们不妨发扬一下极客精神,一起来做一个统计实验:
public class TestSelectionSort {public static void selectionSort(int[] arr) {int countI = 0;int countJ = 0;int countArr = 0;int minIndex;countI++;for (int i = 0; i < arr.length - 1; i++, countI++) {minIndex = i;countJ++;for (int j = i + 1; j < arr.length; j++, countJ++) {if (arr[minIndex] > arr[j]) {// 记录最小值的下标minIndex = j;}countArr++;}// 将最小元素交换至首位int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}int count = countI + countJ + countArr;System.out.println("selectionSort: countI = " + countI + ", countJ = " + countJ + ", countArr = " + countArr + ", count = " + count);}public static void selectionSort2(int[] arr) {int countI = 0;int countJ = 0;int countArr = 0;int minIndex, maxIndex;countI++;// i 只需要遍历一半for (int i = 0; i < arr.length / 2; i++, countI++) {minIndex = i;maxIndex = i;countJ++;for (int j = i + 1; j < arr.length - i; j++, countJ++) {if (arr[minIndex] > arr[j]) {// 记录最小值的下标minIndex = j;}if (arr[maxIndex] < arr[j]) {// 记录最大值的下标maxIndex = j;}countArr += 2;}// 如果 minIndex 和 maxIndex 都相等,那么他们必定都等于 i,且后面的所有数字都与 arr[i] 相等,此时已经排序完成if (minIndex == maxIndex) break;// 将最小元素交换至首位int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;// 如果最大值的下标刚好是 i,由于 arr[i] 和 arr[minIndex] 已经交换了,所以这里要更新 maxIndex 的值。if (maxIndex == i) maxIndex = minIndex;// 将最大元素交换至末尾int lastIndex = arr.length - 1 - i;temp = arr[lastIndex];arr[lastIndex] = arr[maxIndex];arr[maxIndex] = temp;}int count = countI + countJ + countArr;System.out.println("selectionSort2: countI = " + countI + ", countJ = " + countJ + ", countArr = " + countArr + ", count = " + count);}
}
在这个类中,我们用 countI 记录 i 的比较次数,countJ 记录 j 的比较次数,countArr 记录 arr 的比较次数,count 记录总比较次数。
测试用例:
import org.junit.Test;import java.util.ArrayList;public class UnitTest {@Testpublic void test() {ArrayList<Integer> list = new ArrayList<>();for (int i = 0; i <= 1000; i++) {// ArrayList 转 int[]int[] arr = list.stream().mapToInt(Integer::intValue).toArray();System.out.println("*** arr.length = " + arr.length + " ***");TestSelectionSort.selectionSort(arr);TestSelectionSort.selectionSort2(arr);list.add(i);}}
}这里列出部分测试结果:
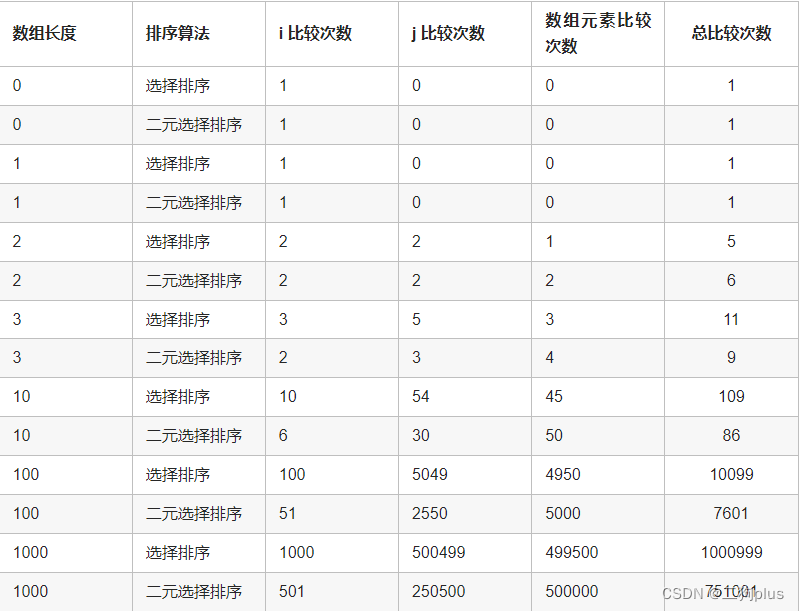
可以看到,二元选择排序中, arr 数组的比较次数甚至略高于选择排序的比较次数,整体是相差无几的。只是 i 和 j 的比较次数较少,正是在这两个地方提高了效率。
并且,在二元选择排序中,我们可以做一个剪枝优化,当 minIndex == maxIndex 时,说明后续所有的元素都相等,就好比班上最高的学生和最矮的学生一样高,说明整个班上的人身高都相同了。此时已经排序完成,可以提前跳出循环。通过这个剪枝优化,对于相同元素较多的数组,二元选择排序的效率将远远超过选择排序。
和选择排序一样,二元选择排序也是不稳定的。
相关文章:

排序算法:选择排序
选择排序的思想是:双重循环遍历数组,每经过一轮比较,找到最小元素的下标,将其交换至首位。 public static void selectionSort(int[] arr) {int minIndex;for (int i 0; i < arr.length - 1; i) {minIndex i;for (int j i …...

Windows运行Spark所需的Hadoop安装
解压文件 复制bin目录 找到winutils-master文件hadoop对应的bin目录版本 全部复制替换掉hadoop的bin目录文件 复制hadoop.dll文件 将bin目录下的hadoop.dll文件复制到System32目录下 配置环境变量 修改hadoop-env.cmd配置文件 注意jdk装在非C盘则完全没问题,如果装在…...

KusionStack使用文档
下载安装 1. 安装 Kusionup 如果想自定义默认安装版本,可以运行下述命令(将最后的 openlatest 替换为你想要默认安装的版本号就就行): curl -s "http://kusion-public.oss-cn-hzfinance.aliyuncs.com/cli/kusionup/script…...
ONLYOFFICE 文档如何与 Alfresco 进行集成
ONLYOFFICE 文档是一款开源办公套件,其是包含文本文档、电子表格、演示文稿、数字表单、PDF 查看器和转换工具的协作性编辑工具。要在 Alfresco 中使用 ONLYOFFICE 协作功能,可以将他们连接集成。阅读本文,了解这如何实现。 关于 ONLYOFFICE…...
PostgreSQL下载路径与安装步骤
PgSQL介绍 PgSQL和MySQL一样是一种关系模型的数据库,全称为PostgreSQL 数据库。 优势:PgSQL是一种可扩展、可靠、可定制的数据库管理系统,具有良好的数据完整性和安全性,支持多种操作系统,包括 Linux、Windows、MacOS …...

如何在PHP中编写条件语句
引言 决策是生活不可缺少的一部分。从平凡的着装决定,到改变人生的工作和家庭决定。在开发中也是如此。要让程序做任何有用的事情,它必须能够对某种输入做出响应。当用户点击网站上的联系人按钮时,他们希望被带到联系人页面。如果什么都没有…...
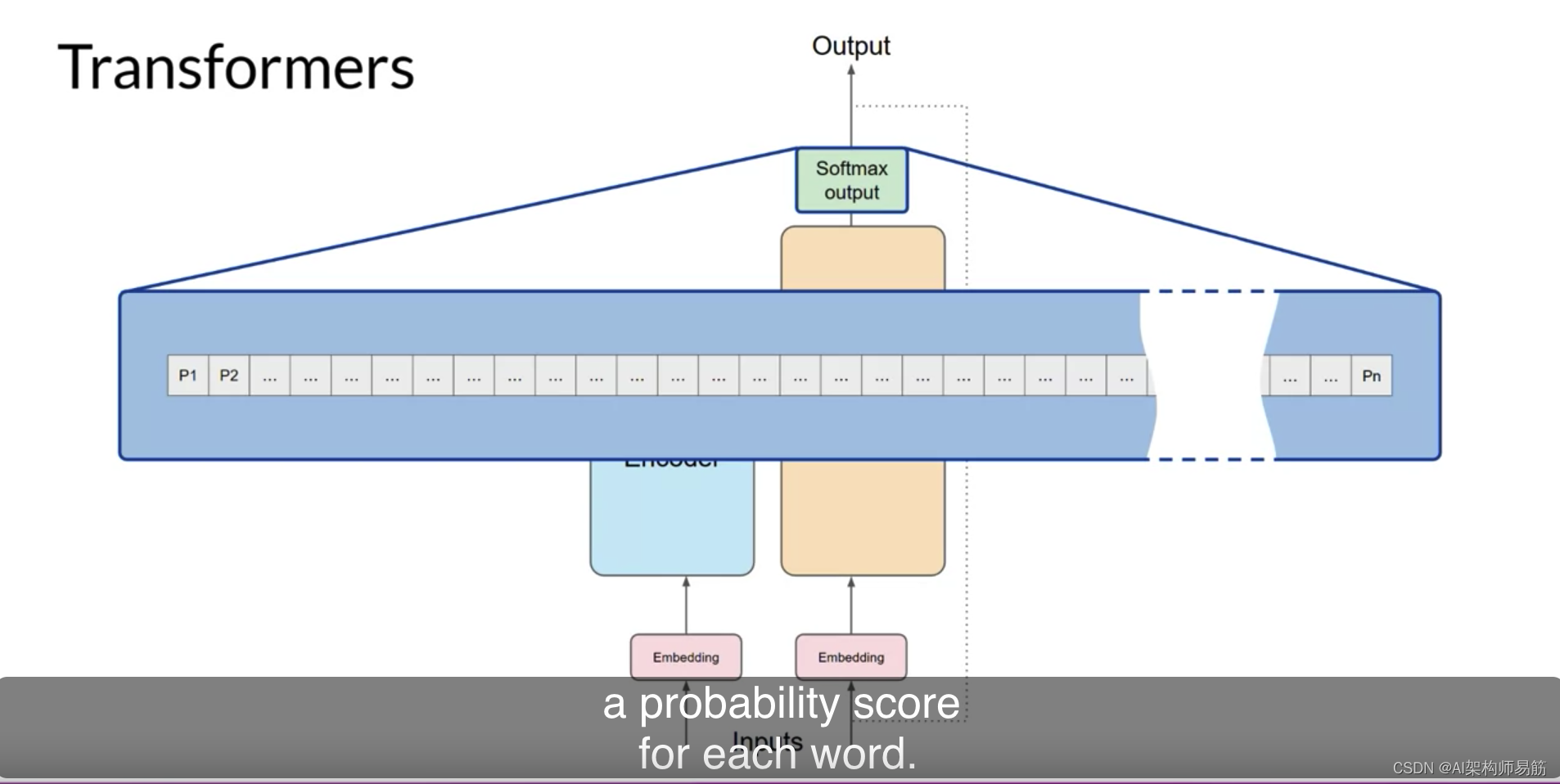
LLM架构自注意力机制Transformers architecture Attention is all you need
使用Transformers架构构建大型语言模型显著提高了自然语言任务的性能,超过了之前的RNNs,并导致了再生能力的爆炸。 Transformers架构的力量在于其学习句子中所有单词的相关性和上下文的能力。不仅仅是您在这里看到的,与它的邻居每个词相邻&…...
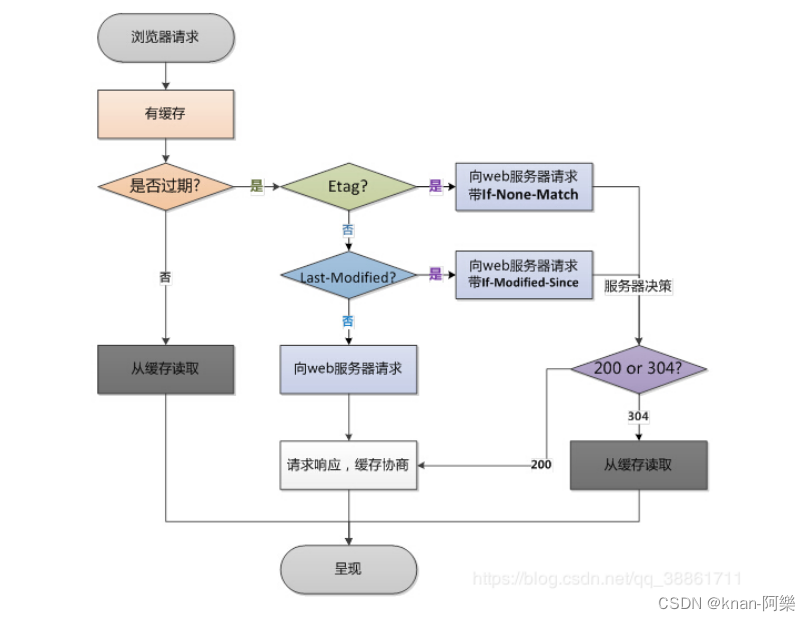
计算机网络 QA
DNS 的解析过程 浏览器缓存。当用户通过浏览器访问某域名时,浏览器首先会在自己的缓存中查找是否有该域名对应的 IP 地址(曾经访问过该域名并且没有清空缓存)系统缓存。当浏览器缓存中无域名对应的 IP 地址时,会自动检测用户计算机…...
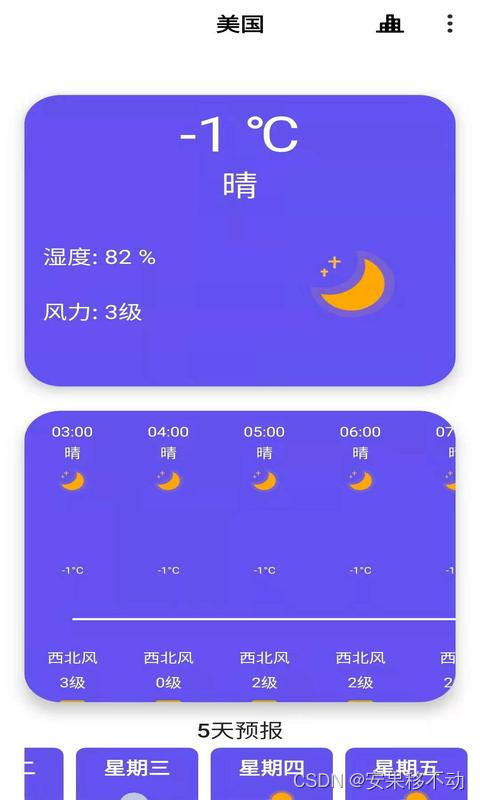
安果天气预报 产品介绍
软件介绍版本号 2.0.5 安果天气预报:全世界覆盖,中国定制 想要查找北京、上海、纽约、东京还是巴黎的天气?一款简约的天气预 报应用为你呈现。专注于为用户提供纯净的天气体验,我们不发送任何打扰的通知。包含空气质量、能见度、…...
net start Mysql 启动服务时 ,显示“Mysql服务正在启动 Mysql服务无法启动 服务没有报告任何错误
一、问题 有时候,输入net start Mysql 启动服务时 mysql>net start Mysql 显示 Mysql服务正在启动 Mysql服务无法启动 服务没有报告任何错误 二、原因 由于mysql的默认端口是3306,因此在启动服务的时候,如果此端口被占用,就会出…...

DAY24
题目一 啊 看着挺复杂 其实很简单 第一种方法 就是纵轴是怪兽编号 横轴是能力值 看看能不能打过 逻辑很简单 看看能不能打得过 打过的就在花钱和直接打里面取小的 打不过就只能花钱 这种方法就导致 如果怪兽的能力值很大 那么我们就需要很大的空间 所以引出下一种做法 纵…...
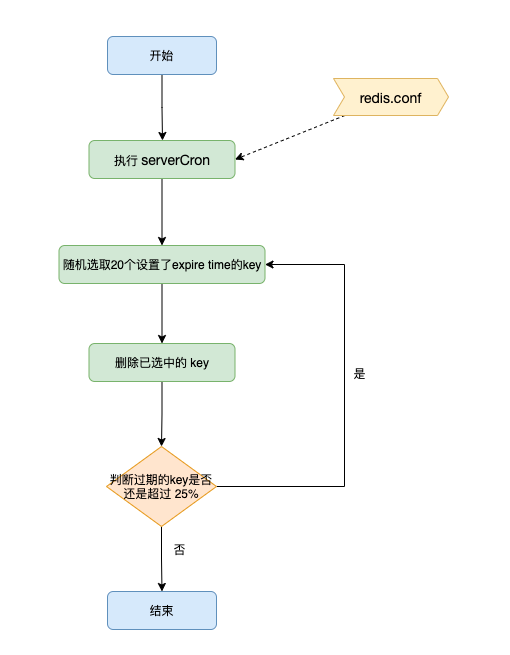
Redis过期数据的删除策略
1 介绍 Redis 是一个kv型数据库,我们所有的数据都是存放在内存中的,但是内存是有大小限制的,不可能无限制的增量。 想要把不需要的数据清理掉,一种办法是直接删除,这个咱们前面章节有详细说过;另外一种就是…...

如何使用CSS实现一个拖拽排序效果?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 实现拖拽排序效果的CSS和JavaScript示例⭐ HTML 结构⭐ CSS 样式 (styles.css)⭐ JavaScript 代码 (script.js)⭐ 实现说明⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦…...

leetcode 118.杨辉三角
⭐️ 题目描述 🌟 leetcode链接:https://leetcode.cn/problems/pascals-triangle/description/ 代码: class Solution { public:vector<vector<int>> generate(int numRows) {// 先开空间vector<vector<int>> v;v.…...

微服务框架之SpringBoot面试题汇总
微服务框架之SpringBoot面试题汇总 什么是Spring Boot? 多年来,随着新功能的增加,spring变得越来越复杂。Spring项目,我们必须添加构建路径或添加Maven依赖关系,配置应用程序服务器,添加spring配置。因此&…...

Promise详解
目录 一、前言:为什么会出现Promise?二、Promise是什么?2.1 Promise的初体验 三、使用Promise的好处?3.1 指定回调函数的方式更加灵活3.2 可以解决回调地狱问题,支持链式调用 四、Promise实例对象的两个属性五、resolve函数以及reject函数六、Promise…...

Oracle 查询(当天,月,年)的数据
Trunc 在oracle中,可利用 trunc函数 查询当天数据,该函数可用于截取时间或者数值,将该函数与 select 语句配合使用可查询时间段数据 查询当天数据 --sysdate是获取系统当前时间函数 --TRUNC函数用于截取时间或者数值,返回指定的…...
什么是梯度下降
什么是梯度下降 根据已有数据的分布来预测可能的新数据,这是回归 希望有一条线将数据分割成不同类别,这是分类 无论回归还是分类,我们的目的都是让搭建好的模型尽可能的模拟已有的数据 除了模型的结构,决定模型能否模拟成功的关键…...
开黑啦kook 机器人开发 PHP swoole Liunx 服务器(宝塔)
安装环境 PHP 拓展 直接使用 宝塔一键安装 (Windows系统不支持) 设置命令行的PHP版本避免执行脚本时 获取不到 swoole 检查swoole是否安装成功 获取官方SDK GitHub - kaiheila/php-bot: 开黑啦机器人的php版本https://github.com/kaiheila/php-bot 配…...
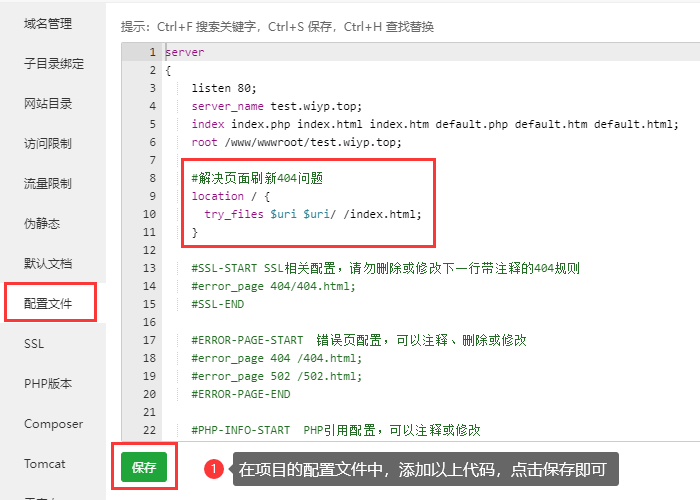
Vue 中hash 模式与 history 模式的区别
hash 模式: - 地址中永远带着 # 号,不美观。 - 兼容性比较好。 - 通过手机 app 分享地址时,如果 app 效验严格,该地址会被标记为不合法。 history 模式: - 地址干净,美观。 - 兼容性和 hash 模式相比…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...
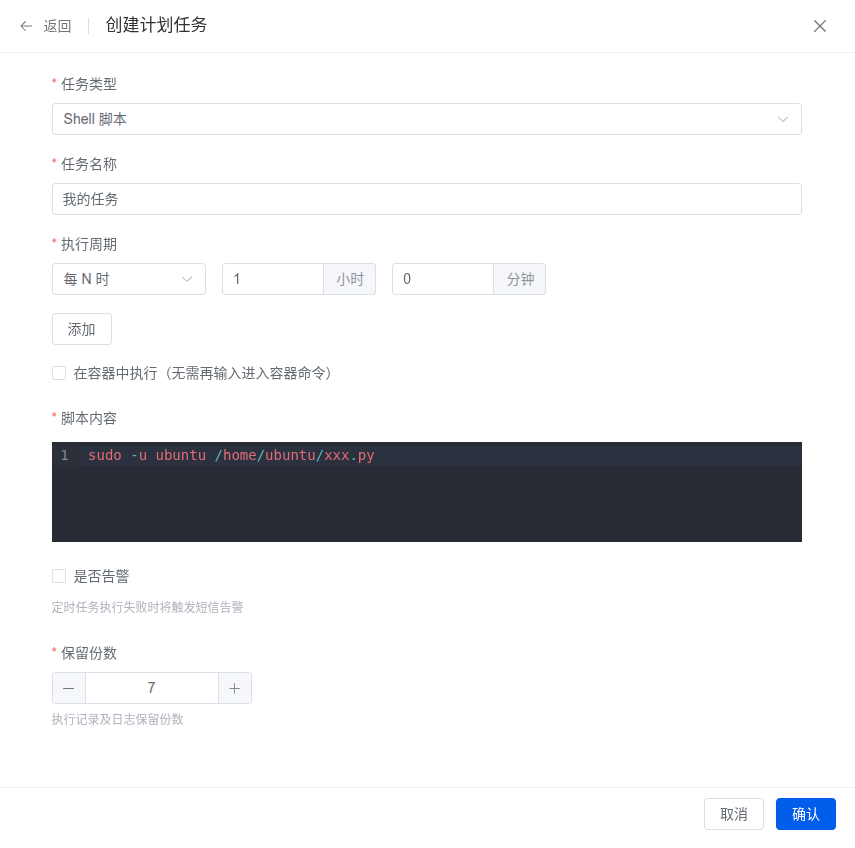
【Linux】使用1Panel 面板让服务器定时自动执行任务
服务器就是一台24小时开机的主机,相比自己家中不定时开关机的主机更适合完成定时任务,例如下载资源、备份上传,或者登录某个网站执行一些操作,只需要编写 脚本,然后让服务器定时来执行这个脚本就可以。 有很多方法实现…...
--uboot系统之外设与PMIC详解)
RK3568项目(七)--uboot系统之外设与PMIC详解
目录 一、引言 二、按键 ------>2.1、按键种类 ------------>2.1.1、RESET ------------>2.1.2、UPDATE ------------>2.1.3、PWRON 部分 ------------>2.1.4、RK809 PMIC ------------>2.1.5、ADC按键 ------------>2.1.6、ADC按键驱动 ------…...
