简述docker的网络模式
Docker 提供了多种网络模式,用于控制容器之间以及容器与主机之间的网络通信。以下是 Docker 的一些常见网络模式
briage模式:
docker容器启动时默认就是该模式,在该模式下,docker容器会连接到一个名为docker0的虚拟以太网桥上,通过NAT(网络地址转发)实现与宿主机网络的通信。容器启动时,使用-p参数进行网络映射,映射过程参考:https://blog.csdn.net/Test_the_rookie/article/details/132407275?spm=1001.2014.3001.5501
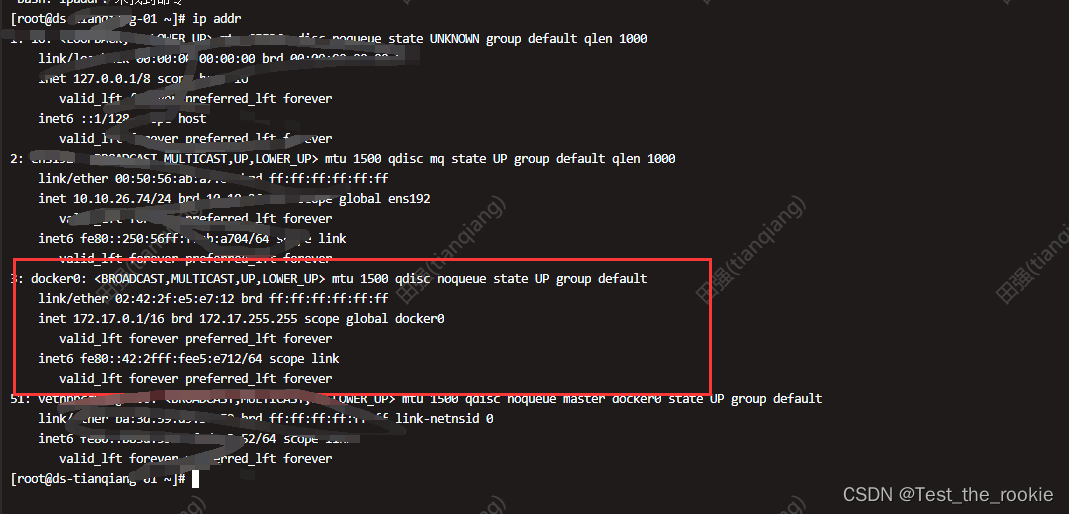
host模式:
在该模式下,容器与宿主机共享网络。容器与宿主机使用相同的网络接口,容器可以直接绑定在宿主机的端口上,无须进行映射即可访问。注意!如果容器内部的程序需要对网络端口进行监听,那么在该模式下,容器内程序监听的网络端口不能与宿主机其他进程的端口冲突。
执行命令:docker run -d --network host image_name 即可使用host模式。进入host模式之后,无须映射,即可访问容器内部程序

使用命令:telnet host_ip:容器内部端口号,发现网络能够正常通信,出现下图即表示你可以直接访问该项目了,而不需要去做映射

none模式:
在此模式下,容器不会附加到任何网络上,容器只能使用本地回环接口,无法与其他主机或者同期通信。在该模式下,容器的网络控件将是一个完全封闭的状态。
执行命令:docker run -d --network none --name none_container mounting_image即可构建一个网络连接模式为none的容器。

执行命令:docker ps --format 'table {{.Names}}\t{{.ID}}\t{{.Image}}\t{{.Networks}}'即可自定义获取到容器的网络模式及各项状态
ps:–format ‘table …’ 是用于在 docker ps 命令中指定输出格式为表格形式的选项
下述两种网络模式仅做了解,具体实现未实操,仅介绍相关的概念。
overlay模式:
在该模式下,允许多个docker主机上的容器在一个逻辑网络中通信,该模式下容器具有了跨主机通信的能力。
macvlan模式:
在该模式下,容器能直接连接到物理网络,,并获得与物理主机上的网络接口类似的功能。在Macvlan模式下,每个容器都被分配一个独立的MAC地址,并且可以通过物理网络接口直接与其他设备通信。
学海无涯
相关文章:

简述docker的网络模式
Docker 提供了多种网络模式,用于控制容器之间以及容器与主机之间的网络通信。以下是 Docker 的一些常见网络模式 briage模式: docker容器启动时默认就是该模式,在该模式下,docker容器会连接到一个名为docker0的虚拟以太网桥上,通…...

MySql-8.0.34 CentOS 安装命令记录
1、执行以下命令获取 glibc 版本,根据版本下载相应的MySQL安装包。 ldd --version 2、下载MySQL。 wget https://dev.mysql.com/get/Downloads/MySQL-8.0/mysql-8.0.34-linux-glibc2.17-x86_64.tar.gz 3、解压 tar -xzvf mysql-8.0.34-linux-glibc2.17-x86_64.t…...

开发电子木鱼功德+1需要多少钱
冥想木鱼小程序是一种结合了冥想和科技的应用形式,为用户提供了随时随地进行冥想的便捷方式。开发一款高质量的冥想木鱼小程序需要综合考虑技术实现、冥想专业性和用户体验等多个方面。本文将详细介绍冥想木鱼小程序的开发过程,并探讨其中的专业性与思考…...

批处理中扩展解释%~的相关知识和用法,并给出示例和实际运行结果展示
批处理中扩展解释%~的相关知识和用法,并给出示例和实际运行结果展示 在批处理脚本中,%~是一个特殊的前缀,用于对参数和变量进行字符串处理。这个前缀后面可以跟着不同的字符,用于执行不同的操作。下面是一些常见的用法:…...

LA@向量组间的表示关系
文章目录 2个向量组间的表示关系向量组的相互表出向量组用另一个向量组表示👺线性表示的系数矩阵矩阵乘法与线性表出列向量组线性表示行向量组线性表示 向量组等价👺向量组等价的性质推论 等价矩阵与向量组等价的关系行等价矩阵的行向量组等价列等价矩阵…...
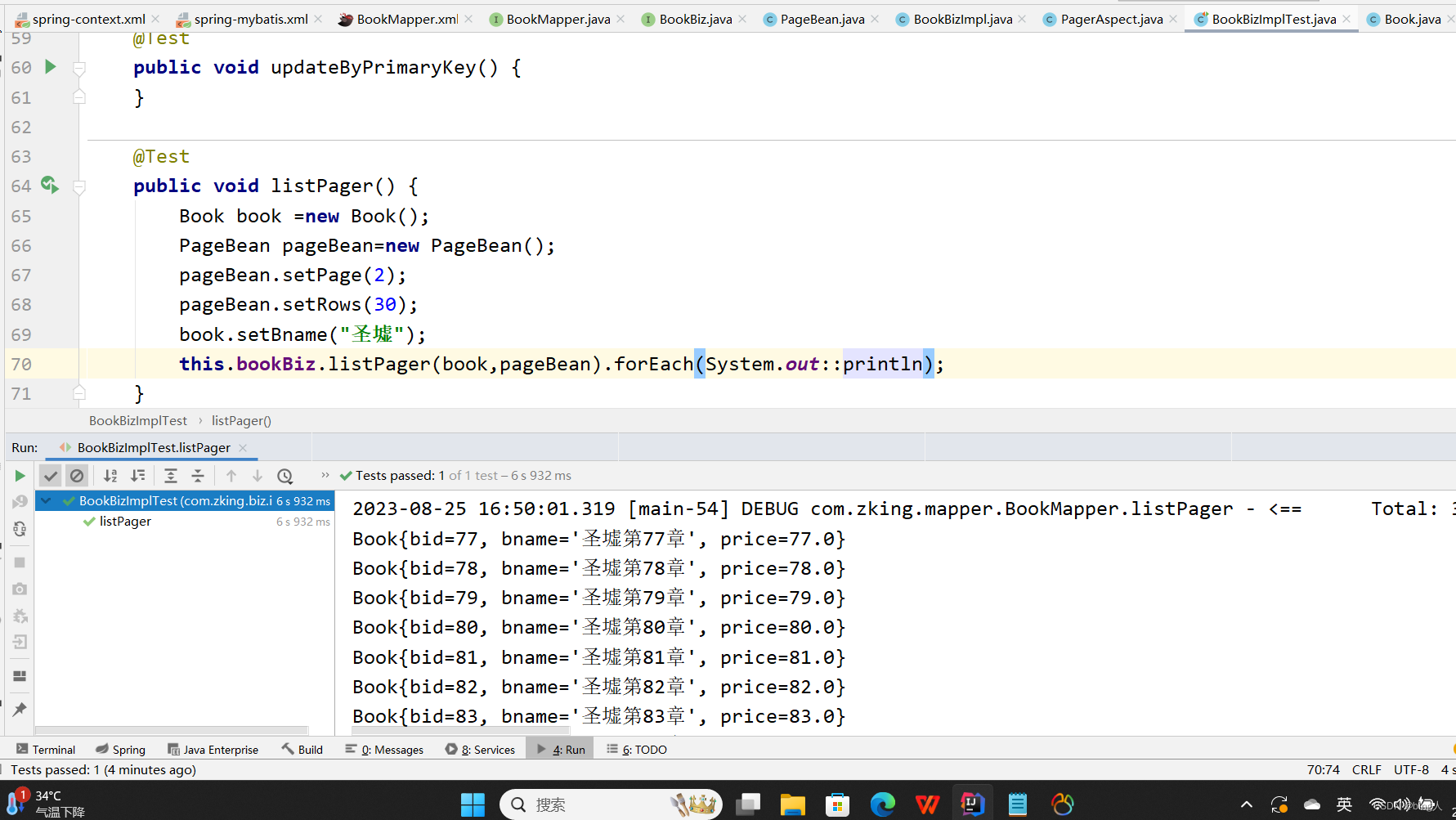
Mybatis与Spring集成
目录 一.Spring整合Mybatis 1.什么是Spring整合Mybatis 新建一个ssm 编辑 导入pom依赖 导入generatorConfig.xml 导入Spring-context.xml文件 导入Spring-mybatis.xml文件 自动生成Bookmapper.xml和Bookmapper文件 编写接口类:Bookbiz 编写接口实现类 …...
AMBA总线协议(0)——目录与传送门
一、AMBA总线协议 Arm高级微控制器总线架构(Advanced Microcontroller Bus Architecture,AMBA)是一种开放式标准片上互联规范,用于连接和管理片上系统(System on Chip,Soc)中的功能块。 AMBA是一种广泛用于…...
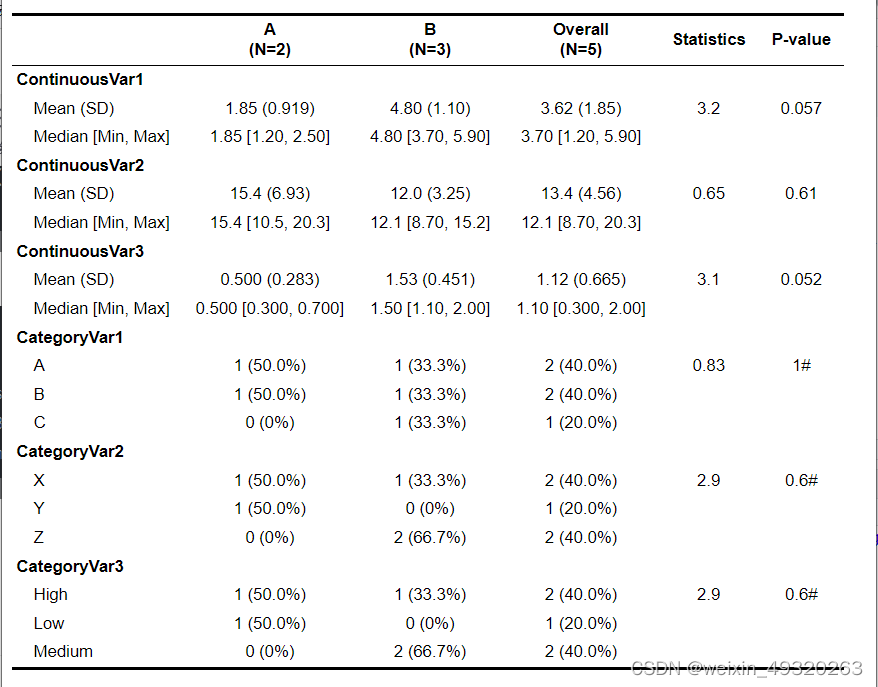
R语言快速生成三线表(1)
R语言的优势在于批量处理,常使用到循环和函数,三线表是科研文章中必备的内容。利用函数实现自动判断数据类型和计算。使用R包(table1)。 # 创建连续性变量 continuous_var1 <- c(1.2, 2.5, 3.7, 4.8, 5.9) continuous_var2 &l…...
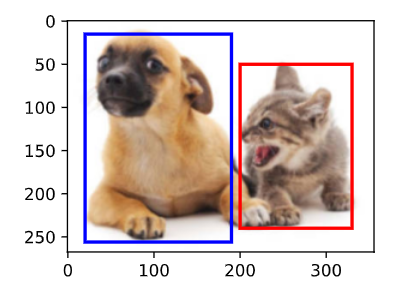
【动手学深度学习】--20.目标检测和边界框
文章目录 目标检测和边界框1.目标检测2.边界框 目标检测和边界框 学习视频:物体检测和数据集【动手学深度学习v2】 官方笔记:目标检测和边界框 在图像分类任务中,我们假设图像中只有一个主要物体对象,我们只关注如何识别其类别…...

实验八 网卡驱动移植
【实验目的】 掌握 Linux 内核配置的基本方法,完成对网卡驱动、NFS 等相关功能的配置 【实验环境】 ubuntu 14.04 发行版FS4412 实验平台交叉编译工具:arm-none-linux-gnueabi- 【注意事项】 实验步骤中以“$”开头的命令表示在 ubuntu 环境下执行&…...

Linux的Man Page知识记录
Man(short for manual) Page是Unix和Linux操作系统中的一个重要文档,提供命令、函数、系统调用等的详细介绍和使用说明。它是以纯文本的形式出现,通常在终端(terminal)中使用man命令访问。Man Page按照章节…...
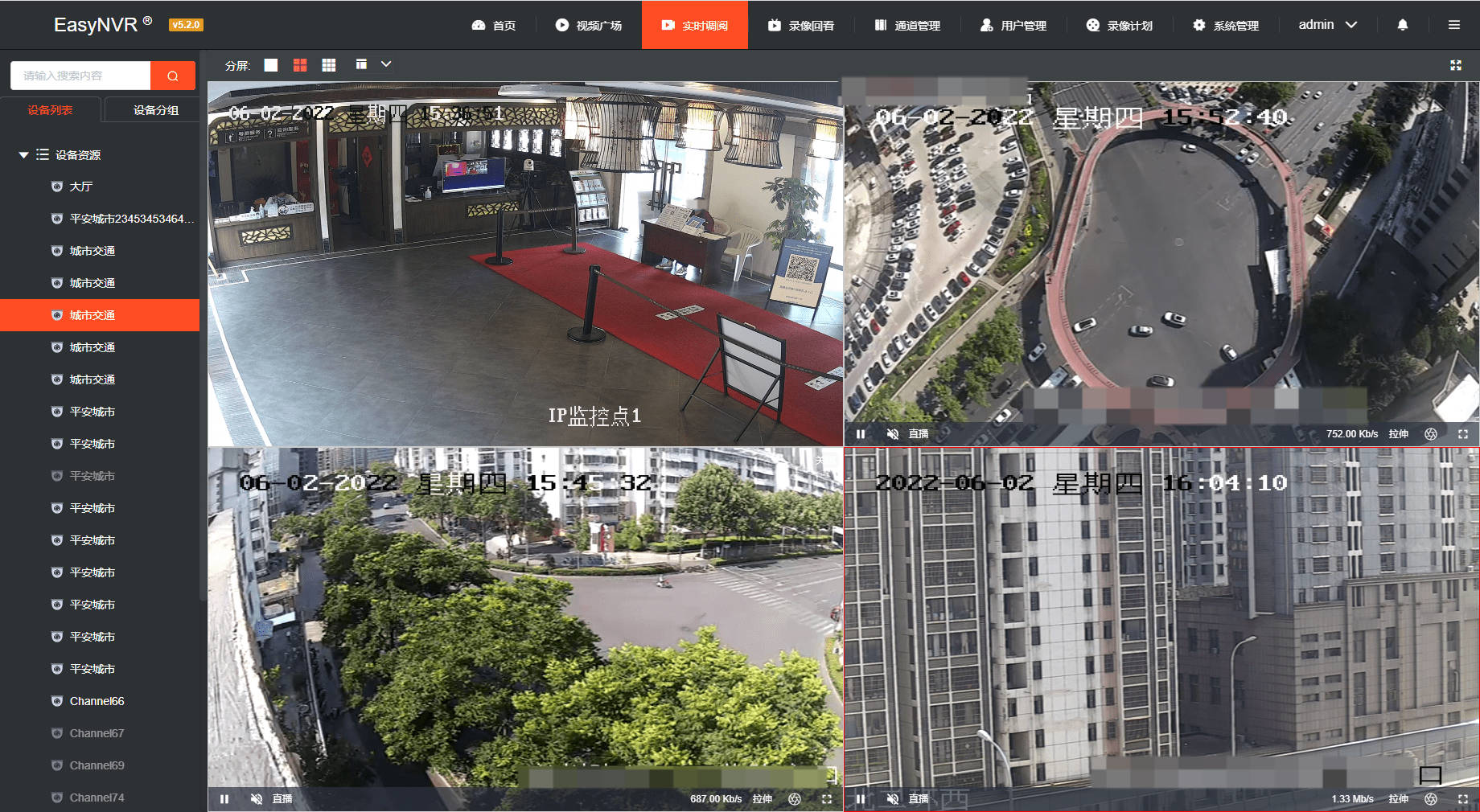
RTSP/Onvif视频服务器EasyNVR安防视频云服务调用接口录像会被自动删除的问题解决方案
EasyNVR安防视频云服务是基于RTSP/Onvif协议接入的视频平台,可支持将接入的视频流进行全平台、全终端的分发,分发的视频流包括RTSP、RTMP、HTTP-FLV、WS-FLV、HLS、WebRTC等。平台丰富灵活的视频能力,可应用在智慧校园、智慧工厂、智慧水利等…...

几个nlp的小项目(文本分类)
几个nlp的小项目(文本分类) 导入加载数据类、评测类查看数据集精确展示数据测评方法设置参数tokenizer,token化的解释对数据集进行预处理加载预训练模型进行训练设置训练模型的参数一个根据任务名获取,测评方法的函数创建预训练模型开始训练本项目的工作完成了什么任务?导…...

MFC——base编码和json数据
目录 1. JSON是什么 2. base64是什么 Base64是一种编解码算法 1. JSON是什么 JSON 是一种数据格式。采用完全独立于语言的文本格式, 因为易读, 易写, 易解析的特性成为理想的数据交换语言。主要有三种类型的值:简单值(字符串, 数字, 布尔, null), 对象, 数组。 长这样的数…...

SQL Server、MySQL和Oracle数据库分页查询的区别与联系
摘要:本文将通过一个现实例子,详细解释SQL Server、MySQL和Oracle这三种常见关系型数据库在分页查询方面的区别与联系。我们将提供具体场景下的SQL语句示例,并解释每个数据库的分页查询用法以及优化方法,帮助读者更好地选择适合自…...
Qt跨平台无边框窗口探索记录
一、前言 实现的效果为:通过黑色矩形框预操作,鼠标释放时更新窗口。效果图如下: 1.功能 1.1 已实现功能 8个方向的缩放标题栏拖动标题栏双击最大化/正常窗口窗口最小尺寸预操作框颜色与背景色互补多屏幕默认标题栏 1.2 待开发功能 拖动到…...

概念解析 | 电磁计算的新篇章:智能电磁计算
注1:本文系“概念解析”系列之一,致力于简洁清晰地解释、辨析复杂而专业的概念。本次辨析的概念是:智能电磁计算。 电磁计算的新篇章:智能电磁计算 随着人工智能的飞速发展,我们正处在一个信息爆炸的时代。各个领域&a…...
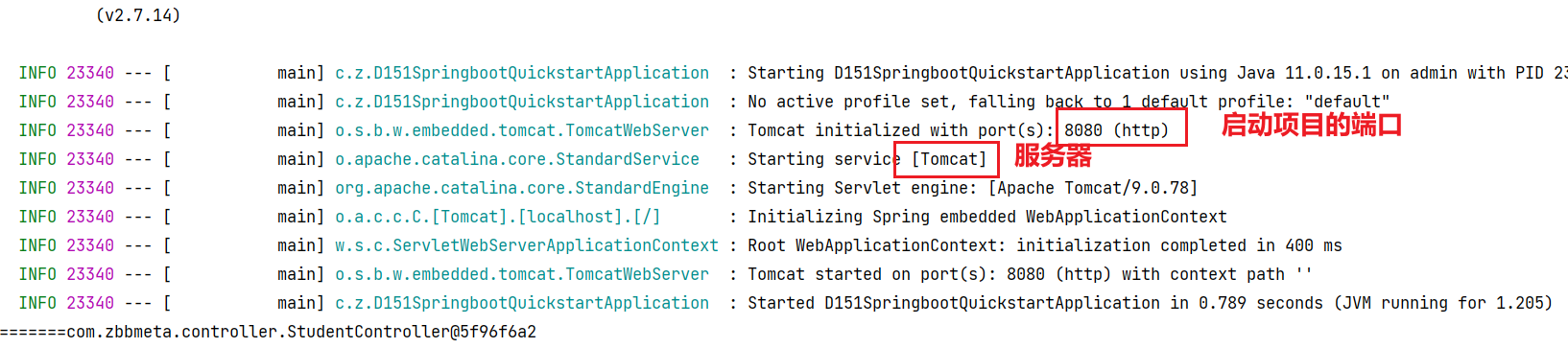
SpringBoot-1-Spring Boot实战:快速搭建你的第一个应用,以及了解原理
SpringBoot-1-Spring Boot实战:快速搭建你的第一个应用,以及了解原理 今日内容 SpringBootWeb入门 前言 我们在之前介绍Spring的时候,已经说过Spring官方(Spring官方)提供很多开源项目,点击projects,看到spring家族…...

Web服务器基础 http协议
文章目录 1.Web基础1.1MIME1.2 URI 和 URL1.2.1定义1.2.2两者的区别 2.静态资源和动态资源2.1 静态资源2.2 动态资源 3.HTTP协议3.1HTTP协议简介3.2HTTP协议的版本及区别3.2.1http协议版本3.2.2http1.0和1.1的区别 3.3HTTP请求报文3.4HTTP请求访问的过程1、建立连接:…...

采用 SVG 实现 web 绘图软件的技术分享
背景 前端技术 使用 svg.js 及全家桶的组件实现 svg 绘图的 web 软件。 MySql8 词语定义 图纸:在页面上绘制的内容整体整体叫做图纸,业务上图纸是具有重要业务意义的概念。 对象:图纸上的业务元素的最小概念。 难点-技术背景 当时遇到…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
