数学建模-规划工具箱yalmip
-
官网下载
-
实例
%% yalmip 求解 yalmip
clc;clear;close all;
%%
%sdpvar实型变量 intvar 整形变量 binvar 0-1型变量
p=sdpvar(3,1); %定义变量
%目标函数 要把求最大值转化为最小值
Objective=-p(1)^2+p(2)^2-p(2)*p(3);%约束条件
Constraints=[0<=p<=1,(p(1)^2+p(1)*p(2)+p(2)*p(3)<=p(2)+6),((2*p(1)+p(2)+3*p(3))<=6)];
%优化求解
optimize(Constraints,Objective)P=double(p);
Obj=double(-Objective);
objstr=['目标函数最优值:',num2str(Obj)];
disp(objstr)
for i=1:length(P)xstr=['x',num2str(i),'的值为:',num2str(P(i))];disp(xstr)
end
%% yalmip 求解
%背包问题
clc;clear;close all;
%sdpvar实型变量 intvar 整形变量 binvar 0-1型变量
%各个物品的质量
w=[80,82,85,70,72,70,82,75,78,45,49,76,45,35,94,49,76,79,84,74,76,63,...35,26,52,12,56,78,16,52, 16,42,18,46,39,80,41,41,16,35,70,72,70,66,50,55,25, 50,55,40];
%各个物品的价值
v=[200,208,198,192,180,180,168,176,182,168,187,138,184,154,168,175,198,...184,158,148,174,135, 126,156,123,145,164,145,134,164,134,174,102,149,134,...156,172,164,101,154,192,180,180,165,162,160,158,155, 130,125];
%%
p=binvar(length(w),1);
%%
%目标函数
%拿出物品价值最大,默认最小值优化,加个负号
Objective=-sum(v*p);
%约束条件
%背包总重量不超过1000
Constraints=[(sum(w*p)<=1000)];
%优化求解
optimize(Constraints,Objective)
P=double(p);
Obj=double(-Objective);
disp(P')
index=find(P==1);
objstr=['目标函数最优值:',num2str(Obj)];
disp(objstr)
disp('装入背包的物品为')
disp(index')
相关文章:

数学建模-规划工具箱yalmip
官网下载 实例 %% yalmip 求解 yalmip clc;clear;close all; %% %sdpvar实型变量 intvar 整形变量 binvar 0-1型变量 psdpvar(3,1); %定义变量 %目标函数 要把求最大值转化为最小值 Objective-p(1)^2p(2)^2-p(2)*p(3);%约束条件 Constraints[0<p<1,(p(1)^2p…...

[SQL挖掘机] - 窗口函数 - 计算移动平均
介绍: 在窗口函数使用时,计算的是累积到当前行的所有的数据的相关操作。 实际上,还可以指定更加详细的汇总范围。该汇总范围称为 框架 (frame)。 其实这里也可以理解成一个窗口, 这个窗口是我们可以进行设置的. 之前我们介绍的窗口函数是根据partition…...

域名和hostname
最近用git克隆远程仓库时总是超时,报错说是代理的问题,但打开和关闭代理都没能解决问题,后面了解到可以关闭git命令的全局代理: git config --global --unset http.proxy git config --global --unset https.proxy如果下次要用的…...
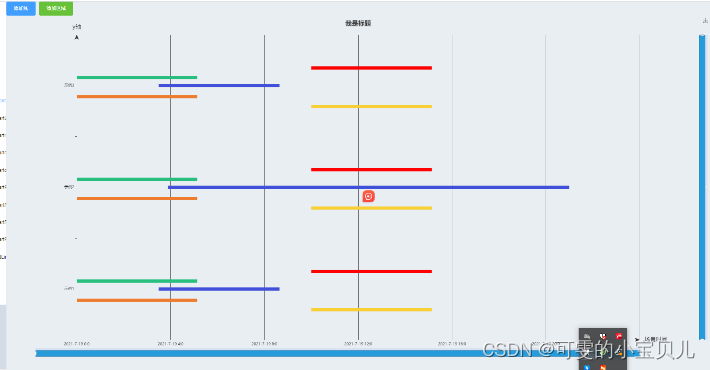
echarts 甘特图一组显示多组数据
<template><el-button type"primary" click"addlin">添加线</el-button><el-button type"success" click"addArea">添加区域</el-button><div ref"echart" id"echart" class&qu…...

1139. 最大的以 1 为边界的正方形;2087. 网格图中机器人回家的最小代价;1145. 二叉树着色游戏
1139. 最大的以 1 为边界的正方形 核心思想:枚举正方向的右下角坐标(i,j),然后你只需要判断四条边的连续一的最小个数即可,这里是边求连续一的个数同时求解结果。 087. 网格图中机器人回家的最小代价 核心…...

css滚动条的使用
前言: css滚动条的使用。 1、使用案例1:背景不要,只展示一个滚动条 如果是默认整体,::就够用了,如果是某个元素,可以 .abc:: ,如果是scss这种的 &:: ::-webkit-scrollbar {width: 6px; } ::-webkit…...

优化Python代理爬虫的应用
当我们在资源受限的环境中使用Python代理爬虫时,我们需要采取一些优化措施,以确保程序的高效性和稳定性。在本文中,我将分享一些关于如何优化Python代理爬虫在资源受限环境下的应用的实用技巧。 首先我们来了解,哪些情况算是资源…...
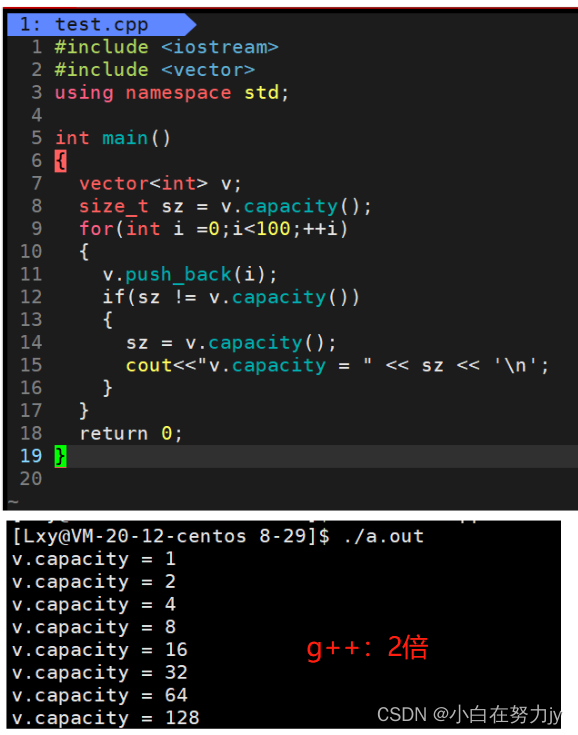
[C++] STL_vector使用与常用接口的模拟实现
文章目录 1、vector的介绍2、vector的使用2.1 vector的定义2.2 vector迭代器的使用2.3 vector的空间增长问题 3、vector的增删查改3.1 push_back(重点)3.2 pop_back(重点)3.3 operator[](重点)3.4 insert3.…...
【LeetCode】167. 两数之和 II - 输入有序数组 - 双指针
目录标题 2023-8-23 09:25:08 2023-8-23 09:25:08 自己写的不是常量级的额外空间,但是写出来了,记录一下。 下次写的时候,请用双指针。 (其实我想了想一想,双指针就没感觉出来:因为我只想到双指针两个都…...

YOLOV1
YOU ONLY LOOK ONCE...
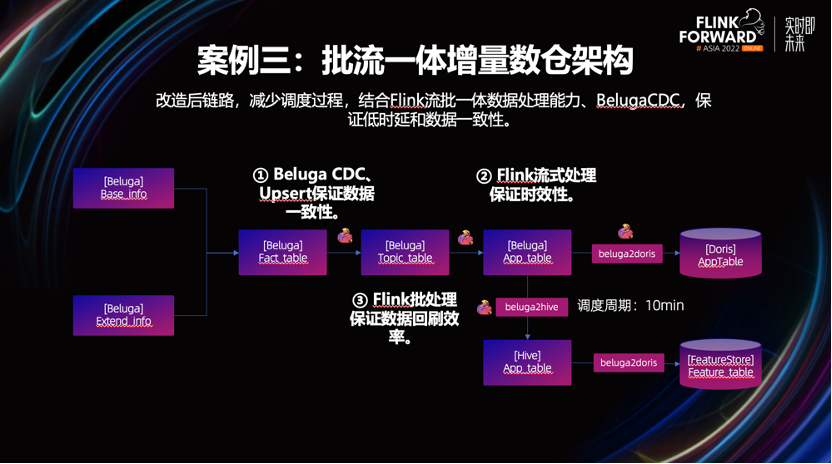
美团增量数仓建设新进展
摘要:本文整理自美团系统研发工程师汤楚熙,在 Flink Forward Asia 2022 实时湖仓专场的分享。本篇内容主要分为四个部分: 建设背景核心能力设计与优化业务实践未来展望 点击查看原文视频 & 演讲PPT 一、美团增量数仓的建设背景 美团数仓架…...

LeetCode解法汇总2337. 移动片段得到字符串
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 描述: 给你两个字…...

Fpass与Fstop
在MATLAB中,“Fpass”、“Fstop”、"Apass"和"Astop"是数字滤波器设计中常用的参数。它们用于定义滤波器的频率响应和滤波器的性能。 "Fpass"表示通带频率,指的是滤波器允许通过的频率范围。在数字滤波器设计中࿰…...
Java快速入门体验
Java快速入门体验 一、环境信息1.1 硬件信息1.2 软件信息 二、Maven安装2.1 Maven介绍2.2 Maven安装包下载2.3 Maven安装2.4 Maven初始化 三、Java安装3.1 JDK下载3.2 JDK安装3.3 JDK初始化 四、开发环境搭建4.1 安装开发工具4.2 关联Maven环境4.2.1 新建JAVA项目4.2.2 Maven与…...

父组件传给子组件的数据是异步的,为什么会导致子组件比父组件先执行?
当父组件传递给子组件的数据是异步获取的时候,可能会导致子组件先执行的问题。这是因为在 Vue 的更新机制中,当组件的模板开始渲染时,会立即触发子组件的创建和挂载过程,而父组件的数据可能还没有完全加载完成。 具体来说…...
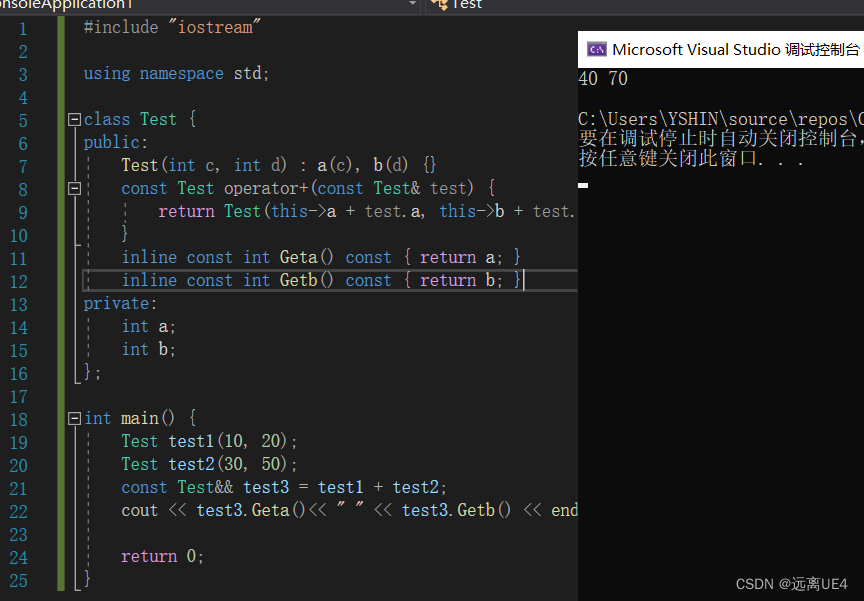
泛型编程 学习笔记
#include "iostream"using namespace std;template<typename T> void Print(T a) {cout << a << endl; }int main() {int a 5;double b 2.3;char c e;string d "sdfasd";Print(a);Print(b);Print(c);Print(d);return 0; } 它可以不用…...

电脑文件删除了可以找回吗?分享一种简单恢复删除电脑文件办法!
电脑文件删除了可以找回吗?可以。在原理上讲电脑删除的文件是有希望恢复的,因为操作系统在删除文件的时候并会不会立刻将文件彻底删除。当文件被删除的时候,其文件记录被删除,并且被文件占用的磁盘空间被标记为空闲。 这样对于用户…...
event模块)
Pygame编程(4)event模块
Pygame编程(4)event模块 函数示例 函数 pygame.event.pump 让 Pygame 内部自动处理事件pygame.event.get 从队列中获取事件pygame.event.poll 从队列中获取一个事件pygame.event.wait 等待并从队列中获取一个事件pygame.event.peek 检测某类型事件是否在…...

Python数据采集实战-使用BeautifulSoup框架解析HTML文档并提取所需内容(附源码和实现效果)
实现功能 使用BeautifulSoup框架解析HTML文档并提取所需内容的例子:假设我们要从以下HTML文档中提取所有超链接的链接地址 实现代码 from bs4 import BeautifulSoup import requests# 发送请求并获取HTML文档 url "https://www.baidu.com" response r…...
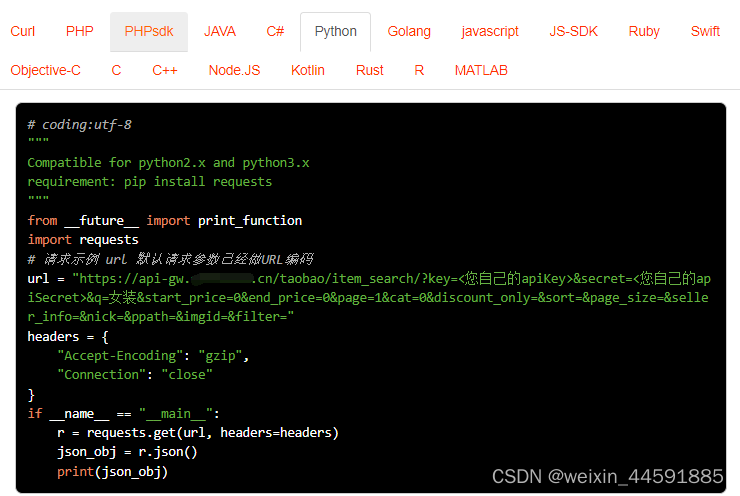
Java“牵手”天猫商品列表数据,关键词搜索天猫商品数据接口,天猫API申请指南
天猫商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取天猫商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问天猫商城的网页来获取商品详情信息。以下是两种常用方法的介绍&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
