机器学习笔记之生成模型综述(三)生成模型的表示、推断、学习任务
机器学习笔记之生成模型综述——表示、推断、学习任务
- 引言
- 生成模型的表示任务
- 从形状的角度观察生成模型的表示任务
- 从概率分布的角度观察生成模型的表示任务
- 生成模型的推断任务
- 生成模型的学习任务
引言
上一节介绍了从监督学习、无监督学习任务的角度介绍了经典模型。本节将从表示、推断、学习三个任务出发,继续介绍生成模型。
生成模型的表示任务
从形状的角度观察生成模型的表示任务
关于概率生成模型,从形状的角度,我们介绍更多的是概率图结构:
-
从概率图结构内部的随机变量结点出发,可以将随机变量划分为两种类型:
- 离散型随机变量(Discrete Random Variable\text{Discrete Random Variable}Discrete Random Variable)
- 连续型随机变量(Continuous Random Variable\text{Continuous Random Variable}Continuous Random Variable)
例如高斯混合模型(Gaussian Mixture Model,GMM\text{Gaussian Mixture Model,GMM}Gaussian Mixture Model,GMM),它的概率图结构表示如下:

其中隐变量Z\mathcal ZZ是一个一维、离散型随机变量,它的概率分布P(Z)\mathcal P(\mathcal Z)P(Z)可表示为:
这里假设Z\mathcal ZZ服从包含K\mathcal KK种分类的Categorial\text{Categorial}Categorial分布。
P(Z)={P1,P2,⋯,PK}∑k=1KPk=1\mathcal P(\mathcal Z) = \{\mathcal P_1,\mathcal P_{2},\cdots,\mathcal P_{\mathcal K}\} \quad \sum_{k=1}^{\mathcal K} \mathcal P_{k}= 1P(Z)={P1,P2,⋯,PK}k=1∑KPk=1
当隐变量Z\mathcal ZZ确定的条件下,对应的观测变量X\mathcal XX是一个服从高斯分布(Gaussian Distribution\text{Gaussian Distribution}Gaussian Distribution)的连续型随机变量。
关于X\mathcal XX的维度,有可能是一维,也有可能是高维。均可用高斯分布进行表示。
P(X∣Z)∼N(μk,Σk)k∈{1,2,⋯,K}\mathcal P(\mathcal X \mid \mathcal Z) \sim \mathcal N(\mu_{k},\Sigma_{k}) \quad k \in \{1,2,\cdots,\mathcal K\}P(X∣Z)∼N(μk,Σk)k∈{1,2,⋯,K} -
从连接随机变量结点的边观察,也可以将边划分为两种类型:
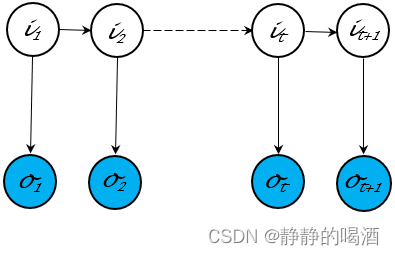
- 有向图模型(Directed Graphical Model\text{Directed Graphical Model}Directed Graphical Model)——由有向边构成的模型,也称贝叶斯网络(Batessian Network\text{Batessian Network}Batessian Network)。代表模型有隐马尔可夫模型(Hidden Markov Model,HMM\text{Hidden Markov Model,HMM}Hidden Markov Model,HMM),其概率图结构表示如下:
有向图的特点是:能够直接观察出随机变量结点之间的因果关系。仅凭概率图结构就可以描述其联合概率分布的因子分解。相反,有向图内部结点的结构关系比较复杂。共包含三种结构(传送门——贝叶斯网络的结构表示)
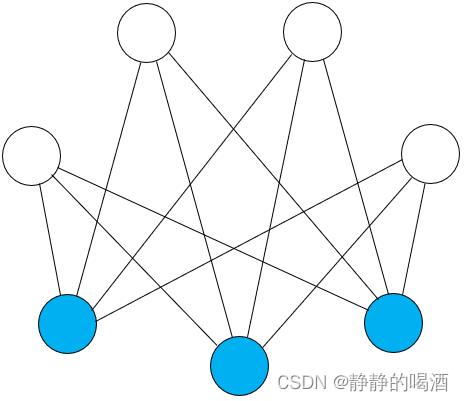
- 无向图模型(Undirected Graphical Model\text{Undirected Graphical Model}Undirected Graphical Model)——由无向边构成的模型,也称马尔可夫随机场(Markov Random Field,MRF\text{Markov Random Field,MRF}Markov Random Field,MRF)。代表模型有受限玻尔兹曼机(Restricted Boltzmann Machine,RBM\text{Restricted Boltzmann Machine,RBM}Restricted Boltzmann Machine,RBM),其概率图结构表示如下:
相比于有向图,无向图的特点是:结点内部结构关系简单,但仅能观察到结点之间存在关联关系而不是因果关系。通过极大团、势函数的方式描述联合概率分布(传送门——马尔可夫随机场的结构表示)
- 有向图模型(Directed Graphical Model\text{Directed Graphical Model}Directed Graphical Model)——由有向边构成的模型,也称贝叶斯网络(Batessian Network\text{Batessian Network}Batessian Network)。代表模型有隐马尔可夫模型(Hidden Markov Model,HMM\text{Hidden Markov Model,HMM}Hidden Markov Model,HMM),其概率图结构表示如下:
-
从随机变量结点类型的角度观察,可以将概率图模型分为两种类型:
- 隐变量模型(Latent Variable Model,LVM\text{Latent Variable Model,LVM}Latent Variable Model,LVM):概率图结构中随机变量结点既包含隐变量、也包含观测变量。上面介绍的几种都属于隐变量模型。还有其他模型如Sigmoid\text{Sigmoid}Sigmoid信念网络等等。
隐变量本身是被假设出来的随机变量,它本身可能不存在实际意义。
- 完全观测变量模型(Fully-Observed Model\text{Fully-Observed Model}Fully-Observed Model):与隐变量模型相反,该模型结构中所有随机变量结点均是观测变量,例如朴素贝叶斯分类器(Naive Bayes Classifier\text{Naive Bayes Classifier}Naive Bayes Classifier):
这意味着概率图结构中的所有随机变量结点均是有真实意义的。

- 隐变量模型(Latent Variable Model,LVM\text{Latent Variable Model,LVM}Latent Variable Model,LVM):概率图结构中随机变量结点既包含隐变量、也包含观测变量。上面介绍的几种都属于隐变量模型。还有其他模型如Sigmoid\text{Sigmoid}Sigmoid信念网络等等。
-
从概率图结构的复杂程度角度观察,可以将其划分为:
- 浅层模型(Shallow Model\text{Shallow Model}Shallow Model): 这里的浅层模型是指没有产生随机变量堆叠的现象。也就是说,没有构建新的随机变量去对原有设定的随机变量进行表示。上述所有介绍的模型均属于浅层模型。
虽然Sigmoid\text{Sigmoid}Sigmoid信念网络也存在‘层级现象’,但这种层级现象中的隐变量结点也不属于深度生成模型。
例如:动态模型如隐马尔可夫模型,虽然它的随机变量结点是基于时间、空间角度无限延伸的,但它同样也是浅层模型。
从浅层模型随机变量结点内部关联关系角度观察,浅层结点内部结点之间关联关系是高度固化的,或者说是稀疏(Sparse\text{Sparse}Sparse)的。
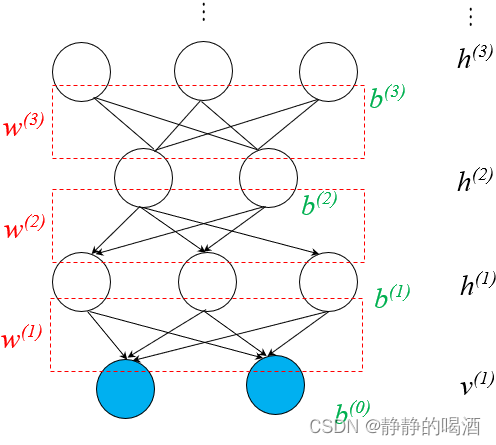
依然使用‘隐马尔可夫模型’举例,由于‘齐次马尔可夫假设’与‘观测独立性假设’的约束,某个隐变量结点只能与‘对应状态的观测变量、下个状态的隐变量’之间存在因果关系。而与其他结点无关。 - 深度生成模型(Deep Generative Model\text{Deep Generative Model}Deep Generative Model):这里的深度指的是深度学习。与上面描述相反,其主要特征是 假设新的随机变量对原有假设的随机变量进行表示。具有代表性的模型有深度信念网络(Deep Belief Network,DBN\text{Deep Belief Network,DBN}Deep Belief Network,DBN):
相反,深度生成模型内部结构中,层与层之间的关联关系是稠密(Dense\text{Dense}Dense)的。
- 浅层模型(Shallow Model\text{Shallow Model}Shallow Model): 这里的浅层模型是指没有产生随机变量堆叠的现象。也就是说,没有构建新的随机变量去对原有设定的随机变量进行表示。上述所有介绍的模型均属于浅层模型。
从概率分布的角度观察生成模型的表示任务
在生成模型综述——生成模型介绍中介绍过,生成模型的关注点均在样本分布自身。那么关于样本分布的概率密度函数P(X)\mathcal P(\mathcal X)P(X)内部的模型参数θ\thetaθ可分为参数化与非参数化两种类型:
-
之前介绍过的绝大多数模型均属于参数化模型(Parameteric Model\text{Parameteric Model}Parameteric Model),可以将模型参数θ\thetaθ看作是未知常量。通过对模型学习得到参数的 解或者是近似解。依然以隐马尔可夫模型为例:
其中π\piπ表示初始状态P(i1)\mathcal P(i_1)P(i1)的概率分布;A\mathcal AA表示状态转移矩阵;B\mathcal BB表示发射矩阵。π,aij,bj(k)\pi,a_{ij},b_j(k)π,aij,bj(k)均属于模型参数。
λ=(π,A,B){π=(p1,p2,⋯,pK)K×1T∑k=1Kpk=1A=[aij]K×Kaij=P(it+1=qj∣it=qi);i,j∈{1,2,⋯,K}B=[bj(k)]K×Mbj(k)=P(ot=vk∣it=qj);j∈{1,2,⋯,K};k∈{1,2,⋯,M}\begin{aligned} & \lambda = (\pi,\mathcal A,\mathcal B) \\ & \begin{cases} \pi = (p_1,p_2,\cdots,p_{\mathcal K})_{\mathcal K \times 1}^T \quad \sum_{k=1}^{\mathcal K} p_k = 1 \\ \mathcal A = [a_{ij}]_{\mathcal K \times \mathcal K} \quad a_{ij} = \mathcal P(i_{t+1} = q_j \mid i_t = q_i);i,j \in \{1,2,\cdots,\mathcal K\} \\ \mathcal B = [b_j(k)]_{\mathcal K \times \mathcal M} \quad b_j(k) = \mathcal P(o_t = v_k \mid i_t = q_j);j \in \{1,2,\cdots,\mathcal K\};k \in \{1,2,\cdots,\mathcal M\} \end{cases} \end{aligned}λ=(π,A,B)⎩⎨⎧π=(p1,p2,⋯,pK)K×1T∑k=1Kpk=1A=[aij]K×Kaij=P(it+1=qj∣it=qi);i,j∈{1,2,⋯,K}B=[bj(k)]K×Mbj(k)=P(ot=vk∣it=qj);j∈{1,2,⋯,K};k∈{1,2,⋯,M}
再例如玻尔兹曼机(Boltzmann Machine,BM\text{Boltzmann Machine,BM}Boltzmann Machine,BM),它的概率密度函数可表示为:
P(v,h)=1Zexp{−E(v,h)}=1Zexp[vTW⋅h+12vTL⋅v+12hTJ⋅h]\begin{aligned} \mathcal P(v,h) & = \frac{1}{\mathcal Z} \exp \{-\mathbb E(v,h)\} \\ & = \frac{1}{\mathcal Z} \exp \left[v^T \mathcal W \cdot h + \frac{1}{2} v^T \mathcal L \cdot v + \frac{1}{2}h^T \mathcal J \cdot h\right] \end{aligned}P(v,h)=Z1exp{−E(v,h)}=Z1exp[vTW⋅h+21vTL⋅v+21hTJ⋅h]
对应需要学习的模型参数可表示为:
其中W,L,J\mathcal W,\mathcal L,\mathcal JW,L,J均以矩阵的形式表示。
θ={W,L,J}\theta = \{\mathcal W,\mathcal L,\mathcal J\}θ={W,L,J} -
无参数化模型(Non-Parameteric Model\text{Non-Parameteric Model}Non-Parameteric Model)主要有高斯过程(Gaussian Process,GP\text{Gaussian Process,GP}Gaussian Process,GP),由于高斯过程在连续域T\mathcal TT内的任意一个时刻均服从高斯分布,因而可以理解为它的模型参数是无限的:
后续尝试介绍‘狄利克雷过程’~
ξti∼N(μti,Σti)ti∈T\xi_{t_i} \sim \mathcal N(\mu_{t_i},\Sigma_{t_i}) \quad t_i \in \mathcal Tξti∼N(μti,Σti)ti∈T
除去参数的角度,从是否直接通过关注样本自身分布P(X)\mathcal P(\mathcal X)P(X)对生成模型进行划分:
-
显式概率密度思想(Explict Density\text{Explict Density}Explict Density):无论是包含隐变量的生成模型如高斯混合模型:
P(X)=∑ZP(X,Z)=∑ZP(Z)⋅P(X∣Z)=∑k=1Kpk⋅N(μk,Σk)∑k=1Kpk=1\begin{aligned} \mathcal P(\mathcal X) & = \sum_{\mathcal Z} \mathcal P(\mathcal X,\mathcal Z) \\ & = \sum_{\mathcal Z} \mathcal P(\mathcal Z) \cdot \mathcal P(\mathcal X \mid \mathcal Z) \\ & = \sum_{k=1}^{\mathcal K} p_k \cdot \mathcal N(\mu_{k},\Sigma_{k}) \quad \sum_{k=1}^{\mathcal K} p_k = 1 \end{aligned}P(X)=Z∑P(X,Z)=Z∑P(Z)⋅P(X∣Z)=k=1∑Kpk⋅N(μk,Σk)k=1∑Kpk=1
还是完全观测变量模型如朴素贝叶斯分类器:需要注意的是,由于是监督学习任务,因此这里的X,Y\mathcal X,\mathcal YX,Y均属于观测变量。因而这里观测变量的概率密度函数是P(X,Y)\mathcal P(\mathcal X,\mathcal Y)P(X,Y)。以二分类为例:第一次转换使用‘贝叶斯定理’P(Y∣X)=P(X,Y)P(X)\mathcal P(\mathcal Y \mid \mathcal X) = \frac{\mathcal P(\mathcal X,\mathcal Y)}{\mathcal P(\mathcal X)}P(Y∣X)=P(X)P(X,Y)由于P(X)=∫YP(X,Y)dY\mathcal P(\mathcal X) = \int_{\mathcal Y}\mathcal P(\mathcal X,\mathcal Y) d\mathcal YP(X)=∫YP(X,Y)dY与Y\mathcal YY无关,被视作常量。因而有:P(Y∣X)∝P(X,Y)\mathcal P(\mathcal Y \mid \mathcal X) \propto \mathcal P(\mathcal X,\mathcal Y)P(Y∣X)∝P(X,Y).
P(Y=0∣X)⇔?P(Y=1∣X)∝P(X,Y=0)⇔?P(X,Y=1)⇒P(Y=1)⋅P(X∣Y=1)⇔?P(Y=0)⋅P(X∣Y=0)\begin{aligned} & \quad \mathcal P(\mathcal Y = 0 \mid \mathcal X) \overset{\text{?}}{\Leftrightarrow} \mathcal P(\mathcal Y =1 \mid \mathcal X) \\ & \propto \mathcal P(\mathcal X,\mathcal Y = 0) \overset{\text{?}}{\Leftrightarrow} \mathcal P(\mathcal X,\mathcal Y = 1) \\ & \Rightarrow \mathcal P(\mathcal Y = 1) \cdot \mathcal P(\mathcal X \mid \mathcal Y = 1) \overset{\text{?}}{\Leftrightarrow} \mathcal P(\mathcal Y = 0) \cdot \mathcal P(\mathcal X \mid \mathcal Y = 0) \end{aligned}P(Y=0∣X)⇔?P(Y=1∣X)∝P(X,Y=0)⇔?P(X,Y=1)⇒P(Y=1)⋅P(X∣Y=1)⇔?P(Y=0)⋅P(X∣Y=0)
它们都属于对样本自身的概率密度函数进行建模。
-
隐式概率密度思想(Implict Density\text{Implict Density}Implict Density):相比之下,这种思路在建模的过程中,并不直接考虑样本自身分布P(X)\mathcal P(\mathcal X)P(X)。例如样本生成任务中,目标是生成与P(X)\mathcal P(\mathcal X)P(X)相似的幻想粒子,但并不是完全得到P(X)\mathcal P(\mathcal X)P(X)之后才能生成,即便是不知道,也可以生成。例如生成对抗网络(Generative Adversarial Networks,GAN\text{Generative Adversarial Networks,GAN}Generative Adversarial Networks,GAN)中的生成器部分:
很明显,生成对抗网络将样本自身概率分布P(X)\mathcal P(\mathcal X)P(X)视作一个复杂函数,使用神经网络的通用逼近定理完成。其输入Z\mathcal ZZ仅是一个简单分布,而该函数描述的是关于X\mathcal XX的后验概率P(X∣Z)\mathcal P(\mathcal X \mid \mathcal Z)P(X∣Z).
X=G(Z,θgene)⇒P(X∣Z)\mathcal X = \mathcal G(\mathcal Z,\theta_{gene}) \Rightarrow \mathcal P(\mathcal X \mid \mathcal Z)X=G(Z,θgene)⇒P(X∣Z)
生成模型的推断任务
关于生成模型推断任务,可以划分为:
- 容易求解(Tractable\text{Tractable}Tractable)的。例如受限玻尔兹曼机的随机变量后验概率的推断任务:
既然是推断任务,模型内部参数均已确定。其中wliw_{li}wli表示隐变量hlh_lhl和观测变量viv_ivi的权重信息;clc_lcl表示偏置信息。
P(hl∣v)={Sigmoid(∑i=1nWli⋅vi+cl)hl=11−Sigmoid(∑i=1nWli⋅vi+cl)hl=0\mathcal P(h_l \mid v) =\begin{cases} \text{Sigmoid}(\sum_{i=1}^n \mathcal W_{li} \cdot v_i + c_l) \quad h_l = 1 \\ 1 - \text{Sigmoid}(\sum_{i=1}^n \mathcal W_{li} \cdot v_i + c_l) \quad h_l = 0 \end{cases}P(hl∣v)={Sigmoid(∑i=1nWli⋅vi+cl)hl=11−Sigmoid(∑i=1nWli⋅vi+cl)hl=0
由于受限玻尔兹曼机的特殊结构假设,可以通过Sigmoid\text{Sigmoid}Sigmoid函数准确描述变量的后验信息。 - 难求解,计算代价极大(Intractable\text{Intractable}Intractable)的。如积分难问题:
P(X)=∫ZP(X,Z)dZ=∫ZP(X∣Z)⋅P(Z)dZ=∫z1⋯∫zKP(X∣Z)⋅P(Z)dz1,⋯,zK\begin{aligned} \mathcal P(\mathcal X) & = \int_{\mathcal Z} \mathcal P(\mathcal X,\mathcal Z) d\mathcal Z \\ & = \int_{\mathcal Z} \mathcal P(\mathcal X \mid \mathcal Z) \cdot \mathcal P(\mathcal Z) d\mathcal Z \\ & = \int_{z_1}\cdots\int_{z_{\mathcal K}} \mathcal P(\mathcal X \mid \mathcal Z) \cdot \mathcal P(\mathcal Z) dz_1,\cdots,z_{\mathcal K} \end{aligned}P(X)=∫ZP(X,Z)dZ=∫ZP(X∣Z)⋅P(Z)dZ=∫z1⋯∫zKP(X∣Z)⋅P(Z)dz1,⋯,zK
生成模型的学习任务
关于生成模型参数的学习任务主要使用极大似然估计(Maximum Likelihood Estimate,MLE\text{Maximum Likelihood Estimate,MLE}Maximum Likelihood Estimate,MLE)。因而可划分为:
- 基于极大似然估计的模型(Likelihood-based Model\text{Likelihood-based Model}Likelihood-based Model):实际上,绝大多数模型均使用的极大似然估计方法。如以受限玻尔兹曼机为代表的能量模型(Energy Model\text{Energy Model}Energy Model):
能量模型参数的学习思想是:基于极大似然估计,求解能量模型的对数似然梯度,最后使用‘梯度上升法’进行近似求解。
logP(v;θ)=log[1Z∑hexp{−E[h,v]}]=log[∑hexp{−E[h,v]}]−log[∑h,vexp{−E[h,v]}]∇θ[logP(v;θ)]=∑h(i),v(i){P(h(i),v(i))⋅∂∂θ[E(h(i),v(i))]}−∑h(i){P(h(i)∣v(i))⋅∂∂θ[E(h(i),v(i))]}θ(t+1)⇐θ(t)+η⋅1N∑v∈V∇θ[logP(v;θ)]\begin{aligned} \log \mathcal P(v;\theta) & = \log \left[\frac{1}{\mathcal Z} \sum_{h} \exp \{- \mathbb E[h,v]\}\right] \\ & = \log \left[\sum_{h} \exp \{-\mathbb E[h,v]\}\right] - \log \left[\sum_{h,v} \exp \{-\mathbb E[h,v]\}\right] \\ \nabla_{\theta} \left[\log \mathcal P(v;\theta)\right] & = \sum_{h^{(i)},v^{(i)}} \left\{\mathcal P(h^{(i)},v^{(i)}) \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} - \sum_{h^{(i)}} \left\{\mathcal P(h^{(i)} \mid v^{(i)}) \cdot \frac{\partial}{\partial \theta} \left[\mathbb E(h^{(i)},v^{(i)})\right]\right\} \\ \theta^{(t+1)} & \Leftarrow \theta^{(t)} + \eta \cdot \frac{1}{N} \sum_{v \in \mathcal V}\nabla_{\theta} \left[\log \mathcal P(v;\theta)\right] \end{aligned}logP(v;θ)∇θ[logP(v;θ)]θ(t+1)=log[Z1h∑exp{−E[h,v]}]=log[h∑exp{−E[h,v]}]−logh,v∑exp{−E[h,v]}=h(i),v(i)∑{P(h(i),v(i))⋅∂θ∂[E(h(i),v(i))]}−h(i)∑{P(h(i)∣v(i))⋅∂θ∂[E(h(i),v(i))]}⇐θ(t)+η⋅N1v∈V∑∇θ[logP(v;θ)] - 与极大似然估计无关的模型(Likelihood-free Model\text{Likelihood-free Model}Likelihood-free Model):最典型的模型依然是生成对抗网络。它使用的是对抗学习思路:
它对判别模型D(X;θd)\mathcal D(\mathcal X;\theta_d)D(X;θd)进行建模,其策略可表示为:
minGmaxD{Ex∼Pdata[logD(x;θd)]+EZ∼P(Z)[log{1−D[G(Z;θgene);θd]}]}\mathop{\min}\limits_{\mathcal G} \mathop{\max}\limits_{\mathcal D} \{\mathbb E_{x \sim \mathcal P_{data}} \left[\log \mathcal D(x;\theta_d)\right] + \mathbb E_{\mathcal Z \sim \mathcal P(\mathcal Z)} \left[\log \{1 - \mathcal D[\mathcal G(\mathcal Z;\theta_{gene});\theta_d]\}\right]\}GminDmax{Ex∼Pdata[logD(x;θd)]+EZ∼P(Z)[log{1−D[G(Z;θgene);θd]}]}
至此,关于生成模型从表示、推断、学习三个任务的区别介绍结束。
相关参考:
生成模型3-表示&推断&学习
相关文章:

机器学习笔记之生成模型综述(三)生成模型的表示、推断、学习任务
机器学习笔记之生成模型综述——表示、推断、学习任务引言生成模型的表示任务从形状的角度观察生成模型的表示任务从概率分布的角度观察生成模型的表示任务生成模型的推断任务生成模型的学习任务引言 上一节介绍了从监督学习、无监督学习任务的角度介绍了经典模型。本节将从表…...
第八章 Flink集成Iceberg的DataStreamAPI、TableSQLAPI详解
1、概述 目前Flink支持使用DataStream API 和SQL API方式实时读取和写入Iceberg表,建议使用SQL API方式实时读取和写入Iceberg表。 Iceberg支持的Flink版本为1.11.x版本以上,以下为版本匹配关系: Flink版本Iceberg版本备注Flink1.11.XI…...

PyTorch学习笔记:nn.Sigmoid——Sigmoid激活函数
PyTorch学习笔记:nn.Sigmoid——Sigmoid激活函数 torch.nn.Sigmoid()功能:逐元素应用Sigmoid函数对数据进行激活,将元素归一化到区间(0,1)内 函数方程: Sigmoid(x)σ(x)11e−xSigmoid(x)\sigma(x)\frac1{1e^{-x}} Sigmoid(x)σ(…...
个人学习系列 - 解决拦截器操作请求参数后台无法获取
由于项目需要使用拦截器对请求参数进行操作,可是请求流只能操作一次,导致后面方法不能再获取流了。 新建SpringBoot项目 1. 新建拦截器WebConfig.java /*** date: 2023/2/6 11:21* author: zhouzhaodong* description:*/ Configuration public class W…...
【编程基础之Python】2、安装Python环境
【编程基础之Python】2、安装Python环境安装Python环境在Windows上安装Python验证Python运行环境在Linux上安装Python验证Python运行环境总结安装Python环境 所谓“工欲善其事,必先利其器”。在学习Python之前需要先搭建Python的运行环境。由于Python是跨平台的&am…...
Java开发 - 问君能有几多愁,Spring Boot瞅一瞅。
前言 首先在这里恭祝大家新年快乐,兔年大吉。本来是想在年前发布这篇博文的,奈何过年期间走街串巷,实在无心学术,所以不得不放在近日写下这篇Spring Boot的博文。在还没开始写之前,我已经预见到,这恐怕将是…...
Office Server Document Converter Lib SDK Crack
关于 Office Server 文档转换器 (OSDC) 无需 Microsoft Office 或 Adobe 软件即可快速准确地转换文档。antennahouse.com Office Server 文档转换器 (OSDC) 会将您在 Microsoft Office(Word、Excel、PowerPoint)中创建的重要文档转换为高质量的 PDF …...

Cubox是什么应用?如何将Cubox同步至Notion、语雀、在线文档中
Cubox是什么应用? Cubox 是一款跨平台的网络收藏工具,通过浏览器扩展、客户端、手机应用、微信转发等方式,将网页、文字、图片、语音、视频、文件等内容保存起来,再经过自动整理、标签、分类之后,就可以随时阅读、搜索…...
计算机网络-传输层
文章目录前言概述用户数据报协议 UDP(User Datagram Protocol)传输控制协议 TCP(Transmission Control Protocol)TCP 的流量控制拥塞控制方法TCP 的运输连接管理TCP 的有限状态机总结前言 本博客仅做学习笔记,如有侵权,联系后即刻更改 科普:…...

HTML-CSS-js教程
HTML 双标签<html> </html> 单标签<img> html5的DOCTYPE声明 <!DOCTYPE html>html的基本骨架 <!DOCTYPE html> <html> </html>head标签 用于定义文档的头部。文档的头部包含了各种属性和信息,包括文档的标题&#…...

【Nacos】Nacos配置中心客户端启动源码分析
SpringCloud项目启动过程中会解析bootstrop.properties、bootstrap.yaml配置文件,启动父容器,在子容器启动过程中会加入PropertySourceBootstrapConfiguration来读取配置中心的配置。 PropertySourceBootstrapConfiguration#initialize PropertySource…...

中国特色地流程管理系统,天翎让流程审批更简单
编者按:本文分析了国内企业在采购流程管理系统常遇到的一些难点,并从适应中国式流程管理模式的特点出发,介绍了符合中国特色的流程审批管理系统——天翎流程管理系统。关键词:可视化开发,拖拽建模,审批控制…...
)
Python算法:DFS排列与组合算法(手写模板)
自写排列算法: 例:前三个数的全排列(从小到大) def dfs(s,t):if st: #递归结束,输出一个全排列print(b[0:n])else:for i in range(t):if vis[i]False:vis[i]Trueb[s]a[i] #存排列dfs(s1,t)vis[i]Falsea[1,2,3,4,…...
拿来就用的Java海报生成器ImageCombiner(一)
背景如果您是UI美工大师或者PS大牛,那本文一定不适合你;如果当您需要自己做一张海报时,可以立马有小伙伴帮您实现,那本文大概率也不适合你。但是,如果你跟我一样,遇上到以下场景,最近公司上了不…...

【C++】类和对象(二)
目录 一、默认成员函数 二、构造函数 1、构造函数概念 2、构造函数编写 3、默认构造函数 4、内置类型成员的补丁 三、析构函数 1、析构函数概念 2、析构函数编写 3、默认析构函数 四、拷贝构造函数 1、拷贝构造函数概念及编写 2、默认拷贝构造函数 3、拷贝构造…...
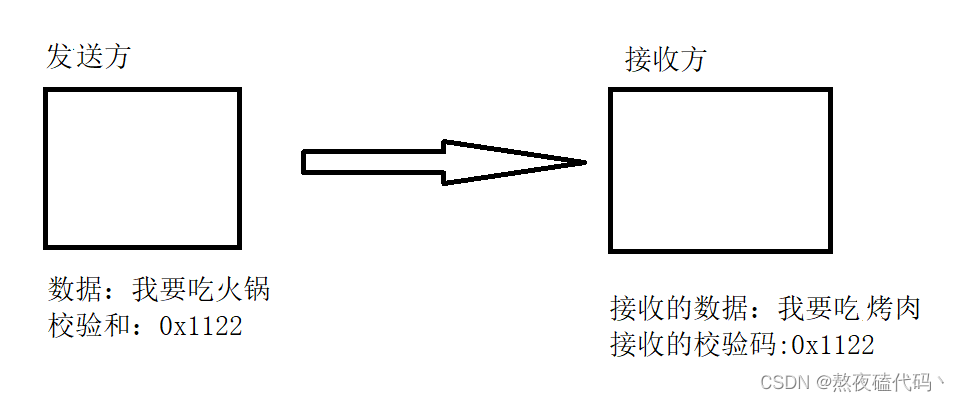
UDP协议
文章目录一、前沿知识应用层传输层二、UDP协议一、前沿知识 应用层 应用层:描述了应用程序如何理解和使用网络中的通信数据。 我们程序员在应用层的主要工作是自定义协议,因为下面四层都在系统内核/驱动程序/硬件中已经实现好了,不能去修改…...

IT人的晋升之路——关于人际交往能力的培养
对于咱们的程序员来说,工作往往不是最难的,更难的是人际交往和关系的维护处理。很多时候我们都宁愿加班,也不愿意是社交,认识新的朋友,拓展自己的圈子。对外的感觉就好像我们丧失了人际交往能力,是个呆子&a…...
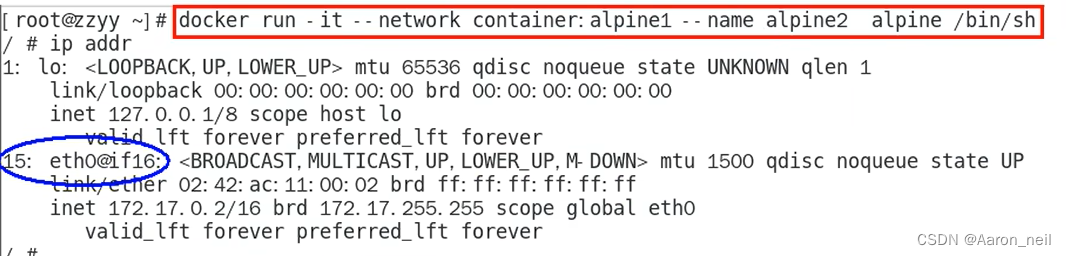
Docker进阶 - 8. docker network 网络模式之 container
目录 1. container 模式概述 2. 使用Alpine操作系统来验证 container 模式 1. container 模式概述 container网络模式新建的容器和已经存在的一个容器共享一个网络ip配置而不是和宿主机共享。新创建的容器不会创建自己的网卡,配置自己的IP,而是和一个…...

2年功能测试月薪9.5K,100多天自学自动化,跳槽涨薪4k后我的路还很长...
前言 其实最开始我并不是互联网从业者,是经历了一场六个月的培训才入的行,这个经历仿佛就是一个遮羞布,不能让任何人知道,就算有面试的时候被问到你是不是被培训的,我还是不能承认这段历史。我是为了生存,…...

“数字孪生”:为什么要仿真嵌入式系统?
01.仿真是什么? 仿真的概念非常广泛,但归根结底都是使用可控的手段来模仿真实的情况,通常应用于现实世界中实施难度大甚至是无法实践的事物。 众所周知,嵌入式系统通常是形式多样的、面向特定应用的软硬件综合体,无…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
