c# 插入排序
插入排序(Insertion Sort):将未排序的元素逐个插入到已排序的序列中的正确位置。
原始数据:{4,3,2,90,10}
第一个循环j=0
首先取出索引为1的元素 3 ,索引为0的元素4,4>3 把4赋值给索引为1的元素 结果为 4 4 2 90 10 然后 j–等于-1
把3赋值给arr[-1+1] 结果为 3 4 2 90 10;
第二个循环 j=1
首先取出索引为1的元素4,索引为2的元素2,4>2把4赋值给索引为2的元素 3结果为 3 4 4 90 10 然后 j-- 等于0
把2赋值给索引为1的元素 结果为 3 2 4 90 10 3>2 把 3赋值给索引1的元素 2结果为 3 3 4 90 10 然后l–等于-1 退出循环
然后arr[-1+1]=2,最终结果为2 3 4 90 10
… 以此类推
public static void Sort(int[] arr){//{4, 3, 2, 90, 10 }int n = arr.Length;//5for (int i = 1; i < n; i++){int key = arr[i];int j = i - 1;// 将 arr[0...i-1] 中的元素移动到比 key 大的位置while (j >= 0 && arr[j] > key){arr[j + 1] = arr[j];j--;}arr[j + 1] = key;}}
相关文章:

c# 插入排序
插入排序(Insertion Sort):将未排序的元素逐个插入到已排序的序列中的正确位置。 原始数据:{4,3,2,90,10} 第一个循环j0 首先取出索引为1的元素 3 ,索引为0的元素4&…...

action和mutation之间的利用 代码解释
场景:购物车点击按钮 context.commit(‘changeCount’, { goodsNum, goodsId })解释这段代码 这段代码是在使用 Vuex 进行状态管理时常见的一种写法。下面对代码进行解释: context.commit 是 Vuex 中的一个方法,用于触发一个名为 changeC…...
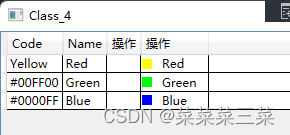
WPF基础入门-Class4-WPF绑定
WPF基础入门 Class4:WPF绑定 1、cs文件中设置需要绑定的数据: public partial class Class_4 : Window{public Class_4(){InitializeComponent();List<Color> test new List<Color>();test.Add(new Color() { Code "Yellow",…...
【广州华锐互动】VR高校虚拟实验教学平台提供丰富的资源支持,提高教学效果
随着科技的不断进步,虚拟现实(VR)技术已经逐渐渗透到各个领域,其中包括教育。 广州华锐互动利用VR虚拟现实技术打造的VR高校虚拟实验教学平台,是一种新型的教学工具,它提供了一个在线的教学资源管理平台,包含教学平台、…...

pytorch学习(7)——神经网络优化器torch.optim
1 optim 优化器 PyTorch神经网络优化器(optimizer)通过调整神经网络的参数(weight和bias)来最小化损失函数(Loss)。 学习链接: https://pytorch.org/docs/stable/optim.html 1.1 优化器基类 使…...

leetcode做题笔记101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。 思路一:递归 bool isSymmetric(struct TreeNode* root){if (root NULL) return true;return fun(root->left, root->right); }int fun(struct TreeNode* l_root, struct TreeNode* r_root) {…...

边缘计算相关概念--学习笔记
一.边缘计算概念 边缘计算将数据的处理,应用程序的运行甚至一些功能服务的实现,由网络中心下放到网络边缘的节点上,在网络边缘侧的智能网关上就近采集并且处理数据,不需要将大量未处理的数据上传到远程的大数据平台。边缘计算理论…...

flutter windows编译错误 flutter_assemble.vcxproj
flutter 编译windows是出现错误。 [ 44 ms] d:\Program Files\Microsoft Visual Studio\2022\Community\MSBuild\Microsoft\VC\v170\Microsoft.CppCommon.targets(248,5): error MSB8066: ��E:\work\kkview_kuaichuan\kkview_kuaichuan\build\windows\C…...

通过运行中的容器生成 Docker Compose 配置文件
背景 笔者之前有一次不小心删除了原始的 docker-compose.yml 文件,不过正在运行的 Docker 容器还在,找了许久,发现一个方法可以从这些容器中生成一个等效的 Docker Compose 配置文件。本文将介绍使用 autocompose 工具从正在运行的容器中反向…...

rancher界面无法登陆问题解决,登录超时;
1.找到rancher主机,查看日志 docker ps | grep rancher # rancher 容器 名称 jolly_ptolemy docker logs -f jolly_ptolemy 日志提示, java.sql.SQLException: Got error 28 from storage engine,磁盘满了 2.磁盘管理 df -h #查看磁盘使…...

Django(6)-django项目自动化测试
Django 应用的测试应该写在应用的 tests.py 文件里。测试系统会自动的在所有以 tests 开头的文件里寻找并执行测试代码。 我们的 polls 应用现在有一个小 bug 需要被修复:我们的要求是如果 Question 是在一天之内发布的, Question.was_published_recentl…...

【AUTOSAR】【CAN通信】CanNm
目录 一、概述 二、说明 三、功能说明 3.1 协调算法 3.2 操作模式 3.2.1 网络模式...

拼多多淘宝大量缓存商品数据用什么格式提供比较好?
众所周知,淘宝拼多多是我国主流的电商平台,其上有大量的商品数据。很多商家会通过API来访问他们的商品数据,根据API的调用次数收费。第三方数据公司提供电商数据接口API,采集实时数据。但是,在他们的服务器上有大量的缓…...

【校招VIP】前端校招考点之页面转换算法
考点介绍: 在地址映射过程中,若在页面中发现所要访问的页面不在内存中,则产生缺页中断。当发生缺页中断时,如果操作系统内存中没有空闲页面,则操作系统必须在内存选择一个页面将其移出内存,以便为即将调入的…...

android 下载网络文件
工具类 import android.app.ProgressDialog; import android.content.Context; import android.os.AsyncTask; import android.os.Environment; import android.util.Log;import java.io.BufferedInputStream; import java.io.File; import java.io.FileOutputStream; import …...

springboot定时任务:同时使用定时任务和websocket报错
背景 项目使用了websocket,实现了消息的实时推送。后来项目需要一个定时任务,使用org.springframework.scheduling.annotation的EnableScheduling注解来实现,启动项目之后报错 Bean com.alibaba.cloud.sentinel.custom.SentinelAutoConfiguration of t…...

CSS3渐变及2D转换
CSS3渐变及2D转换 持续更新哦… 1、css3渐变 概念: CSS3渐变(gradient)可以让你在两个或多个指定的颜色之间显示平 稳的过渡。以前,你必须使用图像来实现这些效果,现在通过使用 CSS3的渐变(gradients)即可实现。此外,渐变效果的元素在放大…...

无涯教程-PHP - eregi()函数
eregi() - 语法 int eregi(string pattern, string string, [array regs]); eregi()函数在pattern指定的整个字符串中搜索string指定的字符串,。搜索不区分大小写。 Eregi()在检查字符串的有效性时特别有用。 可选的输入参数regs包含一个由正则表达式中的括号分组的所有匹配…...

Spring与Mybatis整合aop整合pageHelper分页插件
前言 Spring与MyBatis整合的意义在于提供了一种结合优势的方式,以便更好地开发和管理持久层(数据库访问)代码。 这里也是总结了几点主要意义 简化配置:Spring与MyBatis整合后,可以通过Spring的配置文件来管理和配置M…...
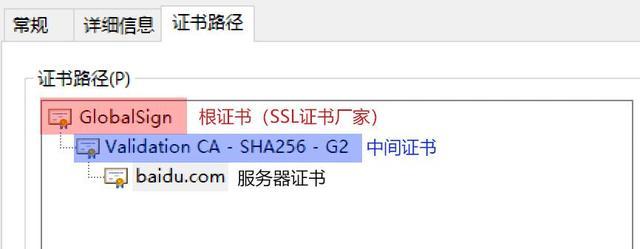
SSL/CA 证书及其相关证书文件(pem、crt、cer、key、csr)
数字证书是网络世界中的身份证,数字证书为实现双方安全通信提供了电子认证。数字证书中含有密钥对所有者的识别信息,通过验证识别信息的真伪实现对证书持有者身份的认证。数字证书可以在网络世界中为互不见面的用户建立安全可靠的信任关系,这…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
