【位运算进阶之----左移(<<)】
今天我们来谈谈左移这件事。
❤️简单来说,对一个数左移就是在其的二进制表达末尾添0。左移一位添一个0,结果就是乘以2;左移两位添两个0,结果就乘以2 ^ 2;左移n位添n个0,结果就是乘以2 ^ n,小心溢出😄!
下面就让我们来详细看看吧!

文章目录
- 一、基础知识:
- :one: 左移的二进制表示:
- :two: 左移的执行结果:
- :three: 对负数左移:
- :four: 左移负数位:
- :five:左移时溢出!
- (1)位溢出(移位/mod的角度):
- (2) 值溢出(值的角度):
- 二、拓展应用:
- 1. 取模和位运算的转换:
- 2. 生成标记码:
- (1. 标记位置1:
- (2. 标记位置0:
- (3. 标记位取反:
- 3. 生成掩码:
一、基础知识:
✨左移操作是一种位操作,用来将一个数的二进制表达的所有位向左移动指定的位数,并在右侧用0填充空位。
1️⃣ 左移的二进制表示:
✨x<<y 表示将x向左移动y位。(其中x和y都是整数)
如:1001 << 2 ----> 100100
2️⃣ 左移的执行结果:
✨左移操作相当于将一个数乘以2的n次方。
x<<y <=> x * (2 ^ y)
如:
#include<stdio.h>int main(void)
{int x = 3, y = 2;printf("%d", x << y);//3*(2^2)return 0;
}
执行结果如下:

如上图可见,3<<2 = 3 * (2^2)= 3*4 = 12;
- 可能聪明的你已经想到了左移的强大之处,即
对1左移时,得到的都是2的幂,这是一个非常重要的知识点❗️
| 1左移n位 | 值 | 2的幂 |
|---|---|---|
| 1<<1 | 2 | 2^1 |
| 1<<2 | 4 | 2^2 |
| 1<<3 | 8 | 2^3 |
| … | … | … |
| 1<<n | 2^n | 2^n |
- 上面我们讨论的左移都是对正整数来说的,那如果对负数呢?对负数左移会发生什么?左移负数位又是如何?阁下莫急,且听我慢慢道来……
3️⃣ 对负数左移:
如:-3<<2 是多少呢?相信你心中已经有答案了,请看下图!
#include<stdio.h>int main(void)
{int x = -3, y = 2;printf("%d", x << y);return 0;
}
执行结果如下:

✨(-x)<<y <=>-(x<<y) :即对负数左移y位等于对正数左移y位后再取负。
这其实也可以用补码来解释:
- -(3<<2):
- 3的补码:00000000 00000000 00000000 00000011
- 3的补码左移两位:00000000 00000000 00000000 00001100=12 ,再取负得12。
- -3<<2:
- -3的补码:11111111 11111111 11111111 11111101
- -3的补码左移两位:11111111 11111111 11111111 11110100
- 转换成原码:10000000 00000000 00000000 00001011+1 = 10000000 00000000 00000000 00001100 = -12。
4️⃣ 左移负数位:
那么,3<<(-2)又是多少呢?😢 放过我吧!💢💢💢
#include<stdio.h>int main(void)
{printf("%d", 32<< (-1));return 0;
}
- 可能有朋友就要类比了,加上-1就是减去1,那么左移-1位是不是右移一位呢?让我们继续往下看:

- 咦,怎么有条波浪线?这是什么?输出怎么会是0?按道理来说r如果是右移那么结果是31/2=16啊!!!

为什么会有警告?难道我想错了?
- 让我们寻着警告去看看到底问题出在哪儿了!
警告1 (点我👈)

警告2(点我👈)

😄看来左移负数位是未定义的行为啊,所以我们最好不要这样写,可能会带来不必要的麻烦,如果想要右移的话就乖乖使用右移操作。
5️⃣左移时溢出!
✨(非溢出)移位可以分为逻辑移位和算术移位。
- 无符号整数:逻辑移位,左、右添0;
- 有符号整数:算术移位,符号位不变,分正负;
✨溢出可以分为位溢出和值溢出(此为博主自己分的,可能不合理,但博主自己觉得合理),而我们又知道,整数分为无符号整数和有符号整数。所以通过组合我们大概了解到,此处的溢出一共有4种情况。
(1)位溢出(移位/mod的角度):
✨对于位溢出来说,我们在上面已经讨论过了,int 类型一共32位,移位大于等于32位或小于0位即为位溢出。
注:在不同的编程语言中,对于超出操作数位数的移位操作,可能会有不同的行为。一些语言会将超出的位数进行取模操作,即将移位的位数先对操作数的位数取模,然后再进行相应的位移,比如C语言❗️❗️❗️
(2) 值溢出(值的角度):
✨当变量的值超过了其所能表达的值的范围时,产生值溢出。但溢出的值并不会消失,而是以另一种形式存在着。
下面我们举例来说明:
❤️有符号整数:
#include<stdio.h>int main(void)
{int a = 9;printf("%d\n", a << 31);printf("%d\n", a << 32);//等价于a<<0;printf("%d", a<<33);//等价于a<<1;return 0;
}
执行结果如下:

如上面的代码所示,a原本是9,其二进制表达为:00000000 00000000 00000000 00001001,现在对其进行左移操作:
1️⃣左移31位:(31<32)未溢出
- 1.从移位的角度来看:
- 第一步,左移31位:10000000 00000000 00000000 00000000(负)
- 第二步,再求出其原码:01111111 11111111 11111111 1111111+1=10000000 00000000 00000000 00000000(先记下符号位,然后各位取反,末位加一,再回归符号位)
- 第三步,可以看出这是最小的数:也即-2^31=-2147483648
- 2.从值的角度来看:
因为9<<31=9 * (2 ^ 31) ,下面我们结合下图来看👇

注:0 和 -2 ^ 31 相对
☝️如上图所示,对于int 类型(有符号整数)的x来说,其范围为:-2 ^ 31 ~ 2 ^ 31-1,当x=2 ^ 31 -1时,x+1将会变为-2 ^ 31,从而我们可以看出越界的本质就是转圈圈。此处1圈是2 ^ 32个数,半圈是2 ^ 31 个数。所以9<<31=9* (2 ^ 31)=4.5* 2 ^ 32=4.5圈,去除整圈,得到0.5圈,从而结果是-2 ^ 31。怎么样,是不是很神奇?
👏当然,也可以通过取模来理解(其实补码的本质就是模运算),将原值与2 ^ 32 取模(因为1圈是2 ^ 32个数),得到2 ^ 31, 但有符号整数上界为2 ^ 31-1,再加一个数将会过渡到最小数 - (2 ^ 31).(此处是有向增加的)
2️⃣左移32位:
- 1.从移位的角度来看:
- 第一步,左移32位:00000000 00000000 00000000 00000000(正)
- 第二步,求出其原码:11111111 11111111 11111111 11111111+1=00000000 00000000 00000000 00000000❗️咦❓怎么是0啊❓上面的结果明明是9啊❗️怎么回事❓

👉这就要考虑到位溢出了!我们上面说过了,C语言会将超出的位数进行取模操作,即将移位的位数对操作数的位数取模,然后进行相应的位移。因为如果直接移位的话,当移位长度大于31时必定是0;因为32>=32,所以32=0(mod(32)),从而原式的值等于00000000 00000000 00000000 00001001左移0位,也就是9本身。
mod可以理解为%运算;
- 2.从值的角度来看:
✨对于上面的9<<32,我们不能仅仅通过表面的移位去观察,而更应该计算一番。
👉因为9<<32=9*(2^32) ,所以原式就等于9圈,刚好是0。😄
3️⃣左移33位与左移32位类似,先对32取模再进行移位。此处不再赘述。
❤️无符号整数:

如上图,☝️
- 无符号整数
unsigned int范围为0~(2 ^ 32)-1,总共也是2 ^ 32个数,但都是非负数。
(2 ^ 32 -1) +1 = 0 ,即结果要对2 ^ 32取模。
#include<stdio.h>int main(void)
{int a = 9;unsigned int b = a ;printf("%d\n", a << 31);printf("%u\n", b<<31);printf("%d\n", a << 32);printf("%u\n", b << 32); return 0;
}
执行结果如下:

注:无符号十进制整数用%u输出;
计算方法根据上图转圈圈就好,此处不再赘述。
二、拓展应用:
1. 取模和位运算的转换:
✨x mod (2 ^ y) = x &((1<<y)-1) 即取x二进制表达后y位。(对于位与的操作可以参考前面的博文)
2. 生成标记码:
✨现将1<<k作为第k个标记位的标记码。(此处取从0开始)
(1. 标记位置1:
✨对于二进制数x,将它的第k位置为1.(从低位开始计位,即从右往左)
置1—>位或:x|(1<<k)
(2. 标记位置0:
✨对于二进制数x,将它的第k位置为0.(从低位开始计位,即从右往左)
置0—>位与:x&(1<<k) ,哦,不不不,不是这样的,应该是x&(~(1<<k))
(3. 标记位取反:
✨对于二进制数x,将它的第k位取反.(从低位开始计位,即从右往左)
取反—>异或:x^(1<<k)
3. 生成掩码:
✨我们可以通过左移来生成一个掩码,从而实现对一个数二进制表达的末k位执行一些操作。
1<<k表示100…00(1加上k个0)(1<<k)-1表示011111(0加上k个1)
从而可以进行以下操作:
🌟将末k位变为1:x|((1<<k)-1)
🌟将末k位变为0:x&(1<<k) 或 x&(~((1<<k)-1))
🌟将末k位都取反:x^((1<<k)-1)
😵好了,今天的讲解就到这里了,相信你也是收获满满吧!
这真的我是肝的最久的一篇文章了,没有之一,从早上肝到了晚上,,,😭😭😭

相关文章:

【位运算进阶之----左移(<<)】
今天我们来谈谈左移这件事。 ❤️简单来说,对一个数左移就是在其的二进制表达末尾添0。左移一位添一个0,结果就是乘以2;左移两位添两个0,结果就乘以2 ^ 2;左移n位添n个0,结果就是乘以2 ^ n,小心…...
石油石化行业网络监控运维方案,全局态势感知,实时预警
石油石化行业是一个高科技密集型行业,投资巨大、人员众多,各产业价值链的关联度较高,大型石油石化企业实现了上中下游产业的一体化协同发展。随着工业4.0时代的来临,信息化和工业化融合,物联网、云计算等新技术的普及推…...

MyBatis 的关联关系配置 一对多,一对一,多对多 关系的映射处理
目录 一.关联关系配置的好处 二. 导入数据库表: 三. 一对多关系:-- 一个订单对应多个订单项 四.一对一关系:---一个订单项对应一个订单 五.多对多关系(两个一对多) 一.关联关系配置的好处 MyBatis是一…...

Diffusion Models for Image Restoration and Enhancement – A Comprehensive Survey
图像恢复与增强的扩散模型综述 论文链接:https://arxiv.org/abs/2308.09388 项目地址:https://github.com/lixinustc/Awesome-diffusion-model-for-image-processing/ Abstract 图像恢复(IR)一直是低水平视觉领域不可或缺的一项具有挑战性的任务&…...
Springboot开发所遇问题(持续更新)
SpringBoot特征: 1. SpringBoot Starter:他将常用的依赖分组进行了整合,将其合并到一个依赖中,这样就可以一次性添加到项目的Maven或Gradle构建中。 2,使编码变得简单,SpringBoot采用 JavaConfig的方式对Spring进行配置…...
智能电视与win10电脑后续无法实现DLNA屏幕共享
问题背景: 我用的是TCL电视,但是并不是最新,打开的方式是U盘->电脑,各位看自己情况,很多问题都大概率是智能电视问题。 情景假设: 假设你已经完成原先智能电视该有的步骤,通过DLNA…...

如何可以管理监督员工工作微信?
自从微信管理系统研发上线之后,为了各企业带来了福音。 很多用户企业都是这样评论微信管理系统的:员工的所有微信聊天记录后台都可以清楚明了的看到,聊天记录都是永久保存的,不担心员工在手机上把聊天记录删除,杜绝员…...

【Django】如何转化已有的数据表到Django模型--20230823
初步生成model.py $ python manage.py inspectdb $ python manage.py inspectdb > models.py python manage.py inspectdb # This is an auto-generated Django model module. # Youll have to do the following manually to clean this up: # * Rearrange models order…...

【C语言】喝汽水问题
大家好!今天我们来学习C语言中的喝汽水问题! 目录 1. 题目内容: 2. 思路分析 2.1 方法一 2.2 方法二 2.3 方法三 3. 代码实现 3.1 方法一 3.2 方法二 3.3 方法三 1. 题目内容 喝汽水,1瓶汽水1元,2个空瓶可以…...
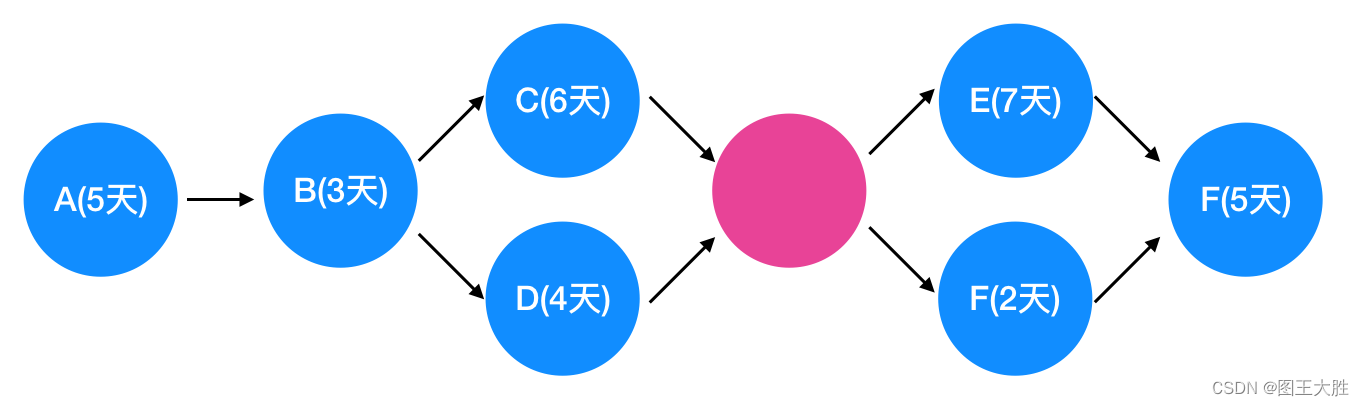
项目进度管理(4-2)关键链法和关键路径法的区别和联系
1 关键链法和关键路径法的主要区别 1.1 关键链法和关键路径法的关注焦点不同 关键路径法(CPM):关注项目中最长的路径,也就是所需时间最长的路径,这被称为关键路径。关键路径决定了项目的最早完成时间。关键链法&…...
基于Java+SpringBoot+Vue前后端分离医院后台管理系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

二维数组传参
在C语言中,可以通过指针来传递二维数组。二维数组实际上是一个连续的内存块,可以使用指针来表示二维数组的行和列。以下是一个示例: #include <stdio.h>void myFunction(int arr[][3], int rows) {for (int i 0; i < rows; i) {fo…...
AI 绘画Stable Diffusion 研究(十四)SD 图生图+剪映制作人物说话视频
大家好,我是风雨无阻。 前一篇,我们详细介绍了使用 SadTlaker制作数字人视频案例,感兴趣的朋友请前往查看:AI 绘画Stable Diffusion 研究(十三)SD数字人制作工具SadTlaker使用教程。 对于没有安装 SadTlaker 插件的朋友…...
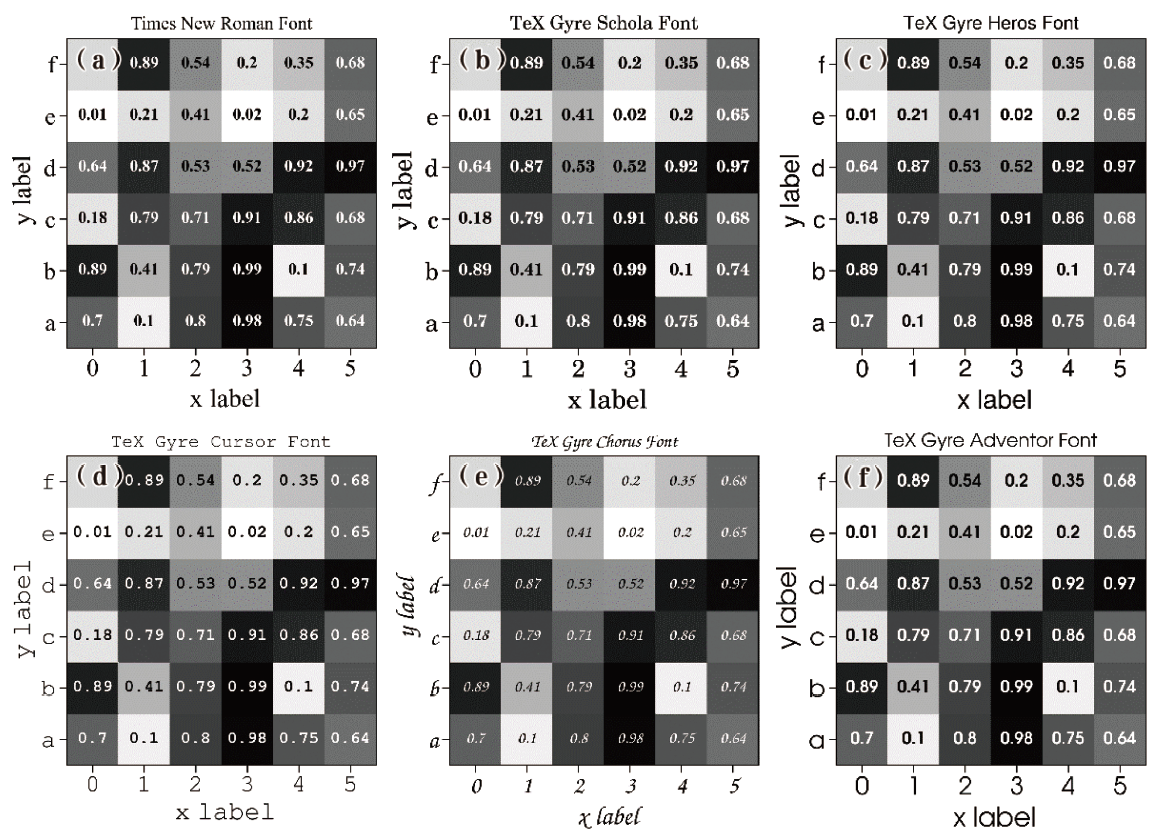
ProPlot 基本语法及特点
文章目录 简介多子图绘制处理共享轴标签“跨度”轴标签多子图序号的绘制 更简单的颜色条和图例更加美观的颜色和字体 简介 科研论文配图多图层元素(字体、坐标轴、图例等)的绘制条件提出了更高要求,我们需要更改 Matplotlib 和 Seaborn 中的…...

element-template-admin get请求正常 post请求超市问题
最近搞全栈,想写个增删改查连接element-template-admin框架,postman测get和post请求都正常,到框架里直接超时,看网络请求一直是padding状态,后来经查阅资料,发现是这个template框架的问题 解决方案&#x…...

Promise.all和promise.race的应用场景举例
Promise.all( ).then( )适用于处理多个异步任务,且所有的异步任务都得到结果时的情况。 <template><div class"box"><el-button type"primary" plain click"clickFn">点开弹出框</el-button></div> &…...

go学习-指针 标识符
指针,以及标识符 1.指针 (1).基本介绍 1)基本数据类型,变量存的值,也叫值类型 2)获取变量的地址用&,比如 var num int ,获取num的地址:&num 3)指针类型&…...
LeetCode--HOT100题(42)
目录 题目描述:108. 将有序数组转换为二叉搜索树(简单)题目接口解题思路代码 PS: 题目描述:108. 将有序数组转换为二叉搜索树(简单) 给你一个整数数组 nums ,其中元素已经按 升序 排列…...
YOLOv8教程系列:三、K折交叉验证——让你的每一份标注数据都物尽其用(yolov8目标检测+k折交叉验证法)
YOLOv8教程系列:三、K折交叉验证——让你的每一份标注数据都物尽其用(yolov8目标检测k折交叉验证法) 0.引言 k折交叉验证(K-Fold Cross-Validation)是一种在机器学习中常用的模型评估技术,用于估计模型的性…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

