时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)
时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)
目录
- 时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)
- 预测效果
- 基本介绍
- 程序设计
- 参考资料
预测效果




基本介绍
Matlab实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测
TSO-XGBoost,金枪鱼算法优化,XGBoost,时间序列预测。
1.data为数据集,单变量时间序列数据集,优化参数(最大迭代次数,深度,学习率),
2.MainTSO_XGboostTS.m为主程序文件,其他为函数文件,无需运行。
3.命令窗口输出R2、MAE、MAE和RMSEP等评价指标,可在下载区获取数据和程序内容。
注意程序和数据放在一个文件夹,文件夹不可以XGBoost命名,因为有函数已经用过,运行环境为Matlab2018及以上。
- xgboost是属于boosting家族,在目标函数中使用了二阶泰勒展开并加入了正则,在决策树的生成过程中采用了精确贪心的思路,寻找最佳分裂点的时候,使用了预排序算法,对所有特征都按照特征的数值进行预排序,然后遍历所有特征上的所有分裂点位,计算按照这些候选分裂点位分裂后的全部样本的目标函数增益,找到最大的那个增益对应的特征和候选分裂点位,从而进行分裂。
- 这样一层一层的完成建树过程, xgboost训练的时候,是通过加法的方式进行训练,也就是每一次通过聚焦残差训练一棵树出来,最后的预测结果是所有树的加和表示。
程序设计
- 完整源码和数据下载地址:MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行%% 优化算法
[Best_pos, Best_score, curve, avcurve] = TSO(pop, Max_iteration, lb, ub, dim, fun);%% 获取最优参数
num_trees = Best_pos(1, 1); % 迭代次数
%params.max_depth = Best_pos(1, 2); % 树的深度
params.max_depth = 18; % 树的深度
params.eta = Best_pos(1, 3); % 学习率%% 建立模型
model = xgboost_train(p_train, t_train, params, num_trees);%% 预测
t_sim1 = xgboost_test(p_train, model);
t_sim2 = xgboost_test(p_test , model);%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1', ps_output);
T_sim2 = mapminmax('reverse', t_sim2', ps_output);%% V. 评价指标
%% 均方根误差 RMSE
error1 = sqrt(sum((T_sim1 - T_train).^2)./M);
error2 = sqrt(sum((T_test - T_sim2).^2)./N);%% 决定系数
R1 = rsquare(T_train,T_sim1);
R2 = rsquare(T_test,T_sim2);MAE1 = mean(abs(T_train - T_sim1));
MAE2 = mean(abs(T_test - T_sim2));
%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1)./T_train));
MAPE2 = mean(abs((T_test - T_sim2)./T_test));
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 适应度曲线
figure
plot(1 : length(curve), curve, 'LineWidth', 1.5);
title('TSO适应度变化曲线', 'FontSize', 13);
xlabel('迭代次数', 'FontSize', 10);
ylabel('适应度值', 'FontSize', 10);
grid onaa=0.7;
z=0.05;
while Iter<Max_iterC=Iter/Max_iter;a1=aa+(1-aa)*C;a2=(1-aa)-(1-aa)*C;for i=1:size(T,1)Flag4ub=T(i,:)>ub;Flag4lb=T(i,:)<lb;T(i,:)=(T(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;fitness(i)=fobj(T(i,:));if fitness(i)<Best_scoreBest_score=fitness(i); Best_pos=T(i,:);endendC_old=T; fit_old=fitness;%-------------------------------------------------t=(1-Iter/Max_iter)^(Iter/Max_iter);if rand<zT(1,:)= (ub-lb)*rand+lb;elseif 0.5<randr1=rand;Beta=exp(r1*exp(3*cos(pi*((Max_iter-Iter+1)/Max_iter))))*(cos(2*pi*r1));if C>randT(1,:)=a1.*(Best_pos+Beta*abs(Best_pos-T(1,:)))+a2.*T(1,:); %Equation (8.3)elseIndivRand=rand(1,dim).*(ub-lb)+lb;T(1,:)=a1.*(IndivRand+Beta*abs(IndivRand-T(1,:)=Best_pos+rand(1,dim).*(Best_pos-T(1,:))+TF.*t^2.*(Best_pos-T(1,:));%Equation (9.1)elseT(1,:) =TF.* t^2.*T(1,:);%Equation (9.2)endendendfor i=2:popif rand<zT(i,:)= (ub-lb)*rand+lb;elseif 0.5<randr1=rand;T(i,:)=a1.*(Best_pos+Beta*abs(Best_pos-T(i,:)))+a2.*T(i-1,:);%Equation (8.4)elseIndivRand=rand(1,dim).*(ub-lb)+lb;T(i,:)=a1.*(IndivRand+Beta*abs(IndivRand-T(i,:)))+a2.*T(i-1,:);%Equation (8.2)endelseTF = (rand>0.5)*2-1;if 0.5>randT(i,:)=Best_pos+rand(1,dim).*(Best_pos-T(i,:))+TF*t^2.*(Best_pos-T(i,:)); %Equation (9.1)elseT(i,:) = TF*t^2.*T(i,:);%Equation (9.2)endendendendIter=Iter+1;curve(Iter)=Best_score;%curve(Iter) = GBestF;avcurve(Iter) = sum(curve) / length(curve);disp(['第' num2str(Iter) '次迭代适应度值:' num2str(Best_score)])
end参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/124693040?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/124864369?spm=1001.2014.3001.5502
相关文章:

时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)
时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价) 目录 时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab实现基于TSO-XGBoost金枪鱼算…...

java- ConcurrentHashMap 并发
1. ConcurrentHashMap 并发 1.1. 减小锁粒度 减小锁粒度是指缩小锁定对象的范围,从而减小锁冲突的可能性,从而提高系统的并发能力。减小锁粒度是一种削弱多线程锁竞争的有效手段,这种技术典型的应用是 ConcurrentHashMap(高性能的 HashMap)…...

java练习8.100m小球落地
题目: 如一个小球从100米高度自由落下,每次落地后就反跳回原高度的一半。 那么求它在第10次落地时,共经过多少米?第10次反弹多高? public static void main(String[] args) {/*假如一个小球从100米高度自由落下,每次落…...

Android JNI系列详解之生成指定CPU的库文件
一、前提 这次主要了解Android的cpu架构类型,以及在使用CMake工具的时候,如何指定生成哪种类型的库文件。 如上图所示,是我们之前使用CMake工具默认生成的四种cpu架构的动态库文件:arm64-v8a、armeabi-v7a、x86、x86_64࿰…...
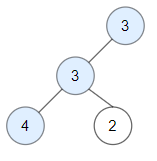
Leetcode每日一题:1448. 统计二叉树中好节点的数目
原题 给你一棵根为 root 的二叉树,请你返回二叉树中好节点的数目。 「好节点」X 定义为:从根到该节点 X 所经过的节点中,没有任何节点的值大于 X 的值。 示例 1: 输入:root [3,1,4,3,null,1,5] 输出:4 解…...

华为OD七日集训第2期 - 按算法分类,由易到难,循序渐进,玩转OD(文末送书)
目录 一、适合人群二、本期训练时间三、如何参加四、7日集训第2期五、精心挑选21道高频100分经典题目,作为入门。第1天、逻辑分析第2天、字符串处理第3天、数据结构第4天、递归回溯第5天、二分查找第6天、深度优先搜索dfs算法第7天、动态规划 六、集训总结1、《代码…...

3d max插件CG MAGIC中的蜂窝材质功能可提升效率吗?
工作中能提升效率也都是大家所想的,对于设计师的一个设计过程中,可能想怎么样可以更快呀,是哪个步骤慢了呢? 这样的结果只能说会很多,但是建模这个步骤,肯定是有多无少的。 为了让模型更加逼真,…...

一句话木马攻击复现:揭示黑客入侵的实战过程
这篇文章旨在用于网络安全学习,请勿进行任何非法行为,否则后果自负。 准备环境 OWASP虚拟机xfp 7与xshell 7 DVWA系统默认的账号密码均为:admin/admin 1、命令注入中复现 攻击payload 127.0.0.1 | echo "<?php eval(…...
【游戏开发教程】Unity Cinemachine快速上手,详细案例讲解(虚拟相机系统 | 新发出品 | 良心教程)
文章目录 一、前言二、插件下载三、案例1:第三人称自由视角,Free Look character场景1、场景演示2、组件参数2.1、CinemachineBrain:核心2.2、CinemachineFreeLook:第三人称自由视角相机2.2.1、设置Follow:跟随2.2.2、…...
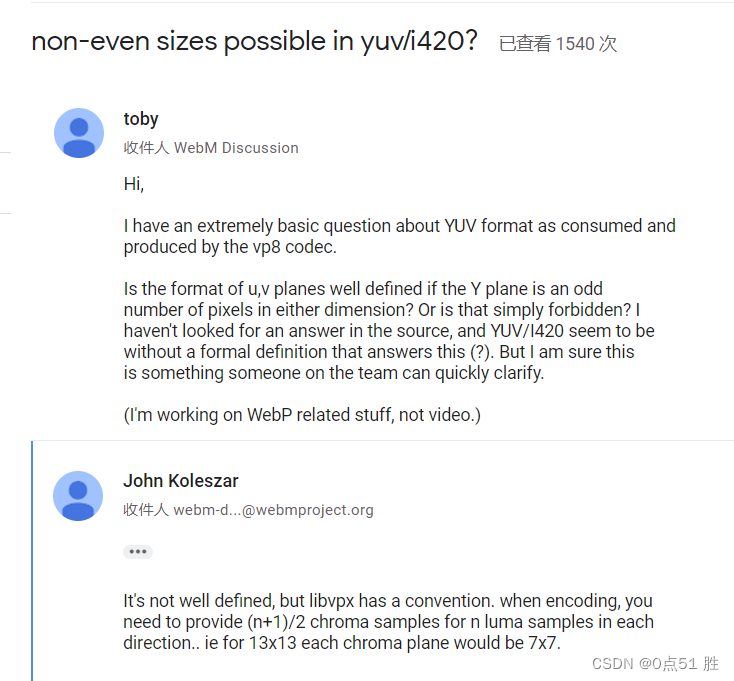
当图像宽高为奇数时,如何计算 I420 格式的uv分量大小
背景 I420 中 yuv 数据存放在3个 planes 中。 网上一般说 I420 数据大小为 widthheight1.5 但是当 width 和 height 是奇数时,这个计算公式会有问题。 I420 中 u 和 v 的宽高分别为 y 的一半。 但是当不能整除时,是如何取整呢?向上还是向下&…...
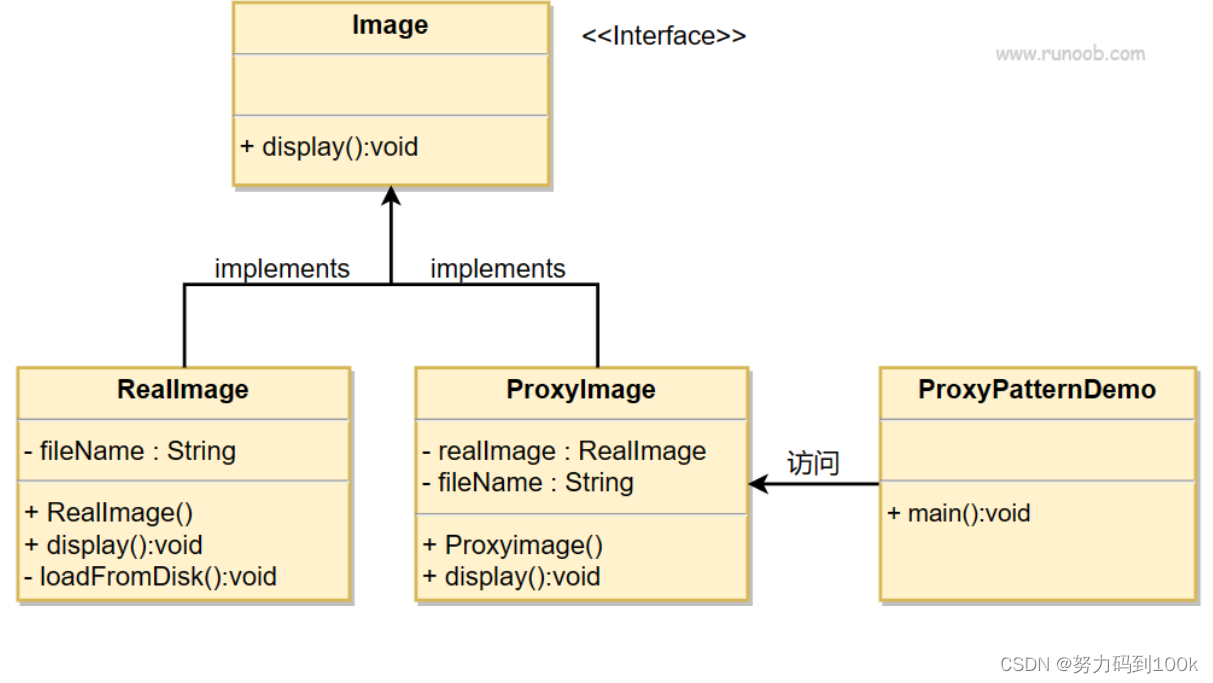
结构型模式-代理模式
代理模式* 定义:在代理模式(Proxy Pattern)中,一个类代表另一个类的功能。这种类型的设计模式属于结构型模式。在代理模式中,我们创建具有现有对象的对象,以便向外界提供功能接口。 意图:为其…...

SpringBoot+Redis BitMap 实现签到与统计功能
最近项目里需要集成签到和统计功能,连续签到后会给用户发放一些优惠券和奖品,以此来吸引用户持续在该品台进行活跃。下面我们一些来聊一聊目前主流的实现方案。 因为签到和统计的功能涉及的数据量比较大,所以在如此大的数据下利用传统的关系…...

P5739 【深基7.例7】计算阶乘
题目描述 求 n ! n! n!,也就是 1 2 3 ⋯ n 1\times2\times3\dots\times n 123⋯n。 挑战:尝试不使用循环语句(for、while)完成这个任务。 输入格式 第一行输入一个正整数 n n n。 输出格式 输出一个正整数,…...
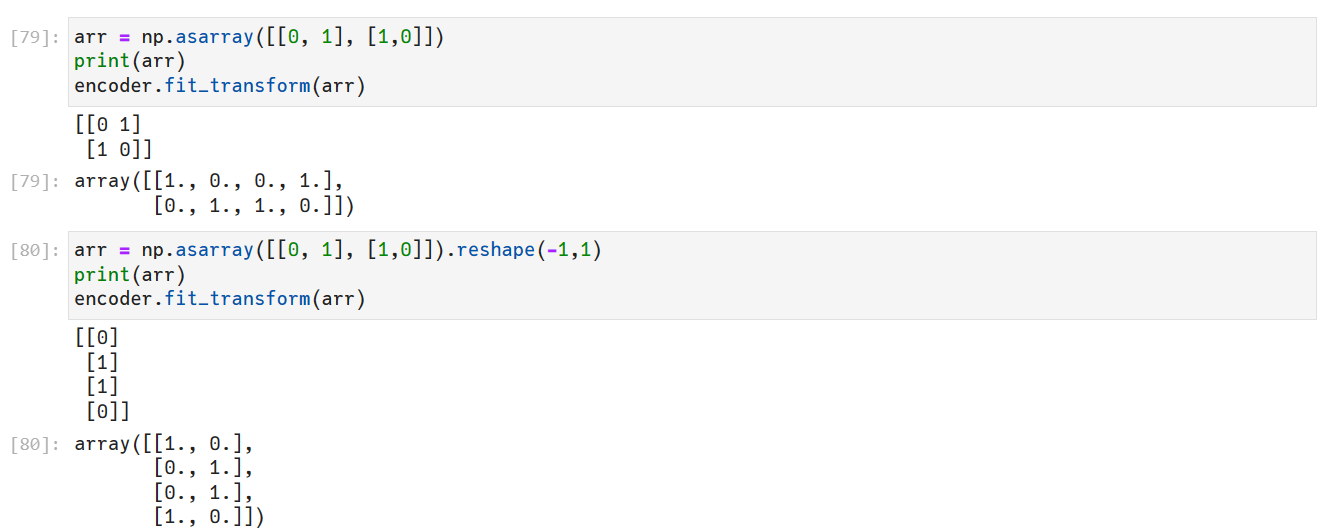
scikit-learn中OneHotEncoder用法
One-Hot编码,又称为一位有效编码,是分类变量作为二进制向量的表示。这首先要求将分类值映射到整数值,然后,每个整数值被表示为二进制向量,将整数索引标记为1,其余都标为0。 OneHotEncoder()常用参数解释 …...
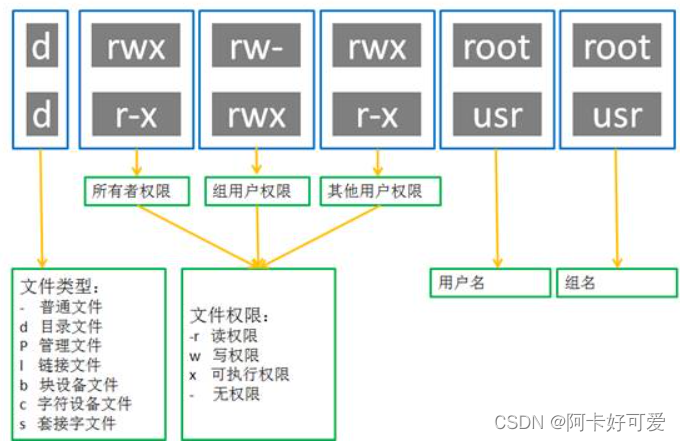
linux操作系统的权限的深入学习(未完)
1.Linux权限的概念 Linux下有两种用户:超级用户(root)、普通用户。 超级用户:可以再linux系统下做任何事情,不受限制 普通用户:在linux下做有限的事情。 超级用户的命令提示符是“#”,普通用户…...
C 连接MySQL8
Linux 安装MySQL 8 请参考文章:Docker 安装MySQL 8 详解 Visual Studio 2022 编写C 连接MySQL 8 C源码 #include <stdio.h> #include <mysql.h> int main(void) {MYSQL mysql; //数据库句柄MYSQL_RES* res; //查询结果集MYSQL_ROW row; //记录结…...

福利之舞:员工的心跳与企业的平衡术
引言:员工福利与满意度的关系 在现代企业中,员工福利已经不仅仅是一种待遇,而是与员工满意度、忠诚度和生产力紧密相连的关键因素。一个合理且吸引人的福利制度可以大大提高员工的工作积极性,同时也能够吸引和留住顶尖的人才。但…...

MyBatis动态语句且如何实现模糊查询及resultType与resultMap的区别---详细介绍
前言 前面我们学习了如何使用Mybatis实现简单的增删改查。今天我们来学习如何使用动态语句来根据不同的条件生成不同的SQL语句。这在实际开发中非常有用,因为通常查询条件是多样化的,需要根据实际情况来拼接SQL语句,那什么是MyBatis动态语句呢…...
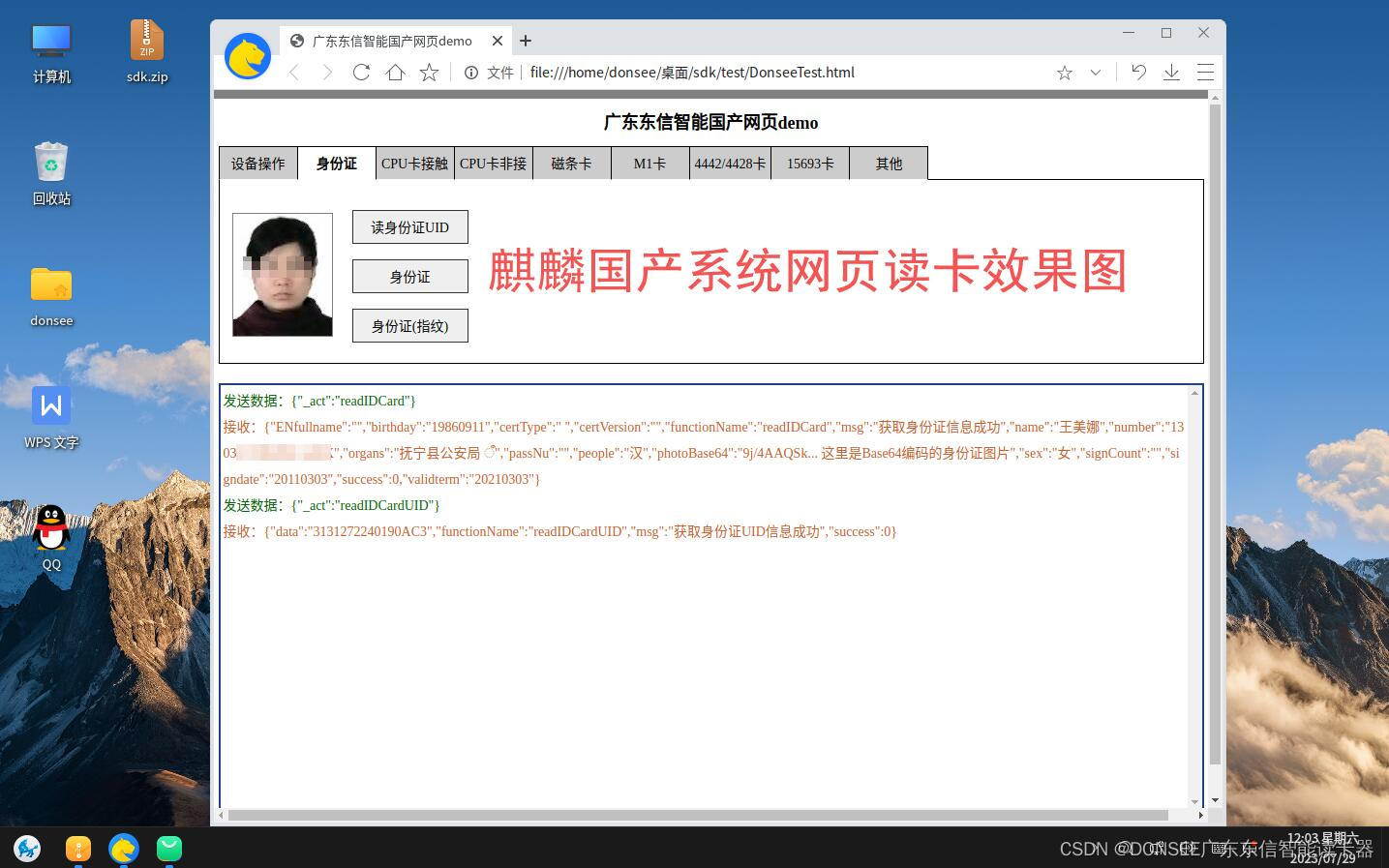
麒麟OS国产系统身份证阅读器web网页开发使用操作流程
1、打开麒麟软件商店,选择驱动,找到身份证阅读器,找到东信智能身份证社保卡读卡器,点击安装。 2、安装完成后,点击打开 3、进入读卡界面 4、进入代码集成 <script type"text/javascript">var ctnFin…...

前端面试:【事件处理】探索事件流、委托与事件对象
嗨,亲爱的事件探险家!在JavaScript的世界中,事件处理是与用户互动的关键。本文将带你探索事件流、事件委托、常见事件类型和事件对象,这些知识将帮助你成为事件处理的大师。 2. 事件流:事件的旅程 事件流描述了事件从…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
