c# 多线程Task.Run 取消正在执行的多线程
c# 异步处理,上次处理没有完成,下次有紧接着处理多线程出错
在 C# 中进行异步处理时,确保处理上一个任务完成后再处理下一个任务是很重要的,特别是在涉及多线程的情况下。如果上一个任务尚未完成,而下一个任务又开始执行,可能会导致竞态条件和数据不一致的问题。为了避免这种情况,可以使用异步编程的相关技术来保证异步任务的有序执行和正确性。以下是一些可能的解决方法:1. **使用 `async` 和 `await`:** 使用 `async` 和 `await` 关键字来编写异步方法,这会在异步任务之间创建一个顺序执行的上下文,确保一个任务完成后再执行下一个任务。```csharp
async Task DoAsyncTasks()
{await FirstTaskAsync();await SecondTaskAsync();// ...
}
```2. **使用 `Task.WhenAll`:** 如果你有多个独立的异步任务,并且你不需要等待每个任务完成后再执行下一个任务,可以使用 `Task.WhenAll` 来等待所有任务完成。```csharp
async Task DoAsyncTasksConcurrently()
{Task task1 = FirstTaskAsync();Task task2 = SecondTaskAsync();await Task.WhenAll(task1, task2);// ...
}
```3. **同步上下文:** 如果你的异步任务需要在特定的同步上下文中执行,比如在 UI 线程中更新 UI,你可以使用 `ConfigureAwait` 来指定需要的上下文。```csharp
async Task UpdateUIAsync()
{await Task.Delay(1000).ConfigureAwait(true); // Run in UI context// Update UI elements here
}
```4. **锁机制:** 如果你在异步任务之间共享资源,确保在访问共享资源时使用适当的同步机制,如 `lock`,以防止竞态条件。```csharp
private async Task AccessSharedResourceAsync()
{lock (syncObject){// Access and modify shared resource here}
}
```总之,在异步编程中,要确保异步任务的有序执行,避免多线程问题,可以使用合适的异步编程技术和同步机制。在处理上一个任务没有完成而下一个任务紧接着处理的情况下,合理地使用 `async`、`await`、`Task.WhenAll` 等工具,以及确保共享资源的同步机制,都能够帮助你避免出现多线程相关的错误。能否取消正在执行的多线程
是的,你可以使用 `CancellationToken` 来取消正在执行的多线程任务。`CancellationToken` 是用于通知任务应该取消的一种机制。你可以在多线程任务中周期性地检查 `CancellationToken`,并在需要的时候停止任务的执行。以下是一个简单的示例,演示如何在多线程任务中使用 `CancellationToken` 进行任务取消:```csharp
using System;
using System.Threading;
using System.Threading.Tasks;namespace CancellationTokenExample
{class Program{static async Task Main(string[] args){CancellationTokenSource cancellationTokenSource = new CancellationTokenSource();CancellationToken cancellationToken = cancellationTokenSource.Token;Task longRunningTask = Task.Run(() => LongRunningOperation(cancellationToken));// 等待一段时间后取消任务await Task.Delay(2000);cancellationTokenSource.Cancel();try{await longRunningTask;}catch (OperationCanceledException){Console.WriteLine("Task was canceled.");}}static void LongRunningOperation(CancellationToken cancellationToken){for (int i = 0; i < 1000; i++){// 检查 CancellationToken 是否被取消if (cancellationToken.IsCancellationRequested){// 执行取消逻辑throw new OperationCanceledException();}Console.WriteLine($"Iteration {i}");Thread.Sleep(500);}}}
}
```在上面的示例中,我们首先创建了一个 `CancellationTokenSource` 对象,并从中获取一个 `CancellationToken`。然后,我们启动了一个长时间运行的任务(`LongRunningOperation`),并在一段时间后通过调用 `Cancel` 方法取消任务。任务在执行期间会周期性地检查 `CancellationToken`,如果被取消,就会抛出 `OperationCanceledException`。注意,在实际多线程应用中,你需要根据任务的性质和要求,合理地在任务代码中检查 `CancellationToken`,并根据需要处理取消情况。这样可以确保任务可以安全地取消,并在取消时进行必要的清理工作。相关文章:

c# 多线程Task.Run 取消正在执行的多线程
c# 异步处理,上次处理没有完成,下次有紧接着处理多线程出错 在 C# 中进行异步处理时,确保处理上一个任务完成后再处理下一个任务是很重要的,特别是在涉及多线程的情况下。如果上一个任务尚未完成,而下一个任务又开始执…...

sql server 如何设置主键
开始之前 限制和局限 一个表只能包含一个 PRIMARY KEY 约束。 在 PRIMARY KEY 约束中定义的所有列都必须定义为 NOT NULL。 如果没有指定为 Null 性,则加入 PRIMARY KEY 约束的所有列的为 Null 性都将设置为 NOT NULL。 创建主键会自动创建相应的唯一群集索引、…...
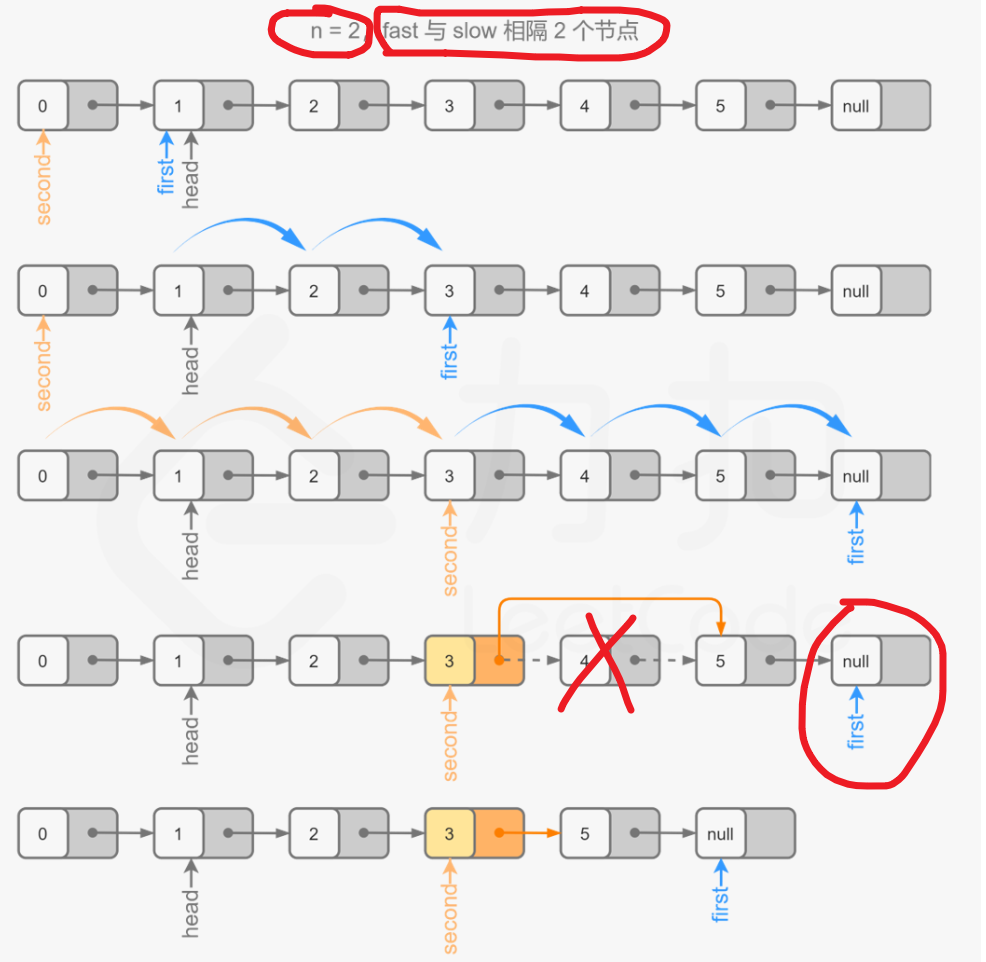
【LeetCode-中等题】19. 删除链表的倒数第 N 个结点
文章目录 题目方法一:节点加入集合找索引方法二:直接计算长度,然后找出要删除的节点的前一个节点方法三:栈方法四:前后双指针 题目 这题的关键在与两个点 一定要设置一个哑结点,防止删除第一个元素时,导致空…...

Matlab图像处理-减法运算
减法运算 图像减法也称为差分方法,是一种常用于检测图像变化及运动物体的图像处理方法。常用来检测一系列相同场景图像的差异,其主要的应用在于检测同一场景下两幅图像之间的变化或是混合图像的分离。 差影法 将同一景物在不同时问拍摄的图像或同一景…...

stm32之11.USART串口通信
可以添加上拉电阻,但会增加功耗,传输距离变长 要添加库函数USART 官方参考文档说明书位置 ALT+左键可实现整体删除(如下图) 输出模式第三种模式AF ---------------------- 源码 远程控制pc端 #include <stm32f4x…...

Python实现T检验
今天来分享一下T检验的python实现方法。 01 先来上一波概念。 1.单样本t检验,又称单样本均数t检验,适用于来自正态分布的某个样本均数与已知总体均数的比较,其比较目的是检验样本均数所代表的总体均数是否与已知总体均数有差别。已知总体均数…...

校招算法题实在不会做,有没有关系?
文章目录 前言一、校招二、时间复杂度1、单层循环2、双层循环 三、空间复杂度四、数据结构五、校招算法题实在不会做,有没有关系?六、英雄算法集训 前言 英雄算法联盟八月集训 已经接近尾声,九月算法集训将于 09月01日 正式开始,目…...

Michael.W基于Foundry精读Openzeppelin第32期——SignatureChecker.sol
Michael.W基于Foundry精读Openzeppelin第32期——SignatureChecker.sol 0. 版本0.1 SignatureChecker.sol 1. 目标合约2. 代码精读2.1 isValidSignatureNow(address signer, bytes32 hash, bytes memory signature) 0. 版本 [openzeppelin]:v4.8.3,[for…...

如何修改字符串内容?
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈Java 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 String 1. 修改字符串2. StringBuilder和…...
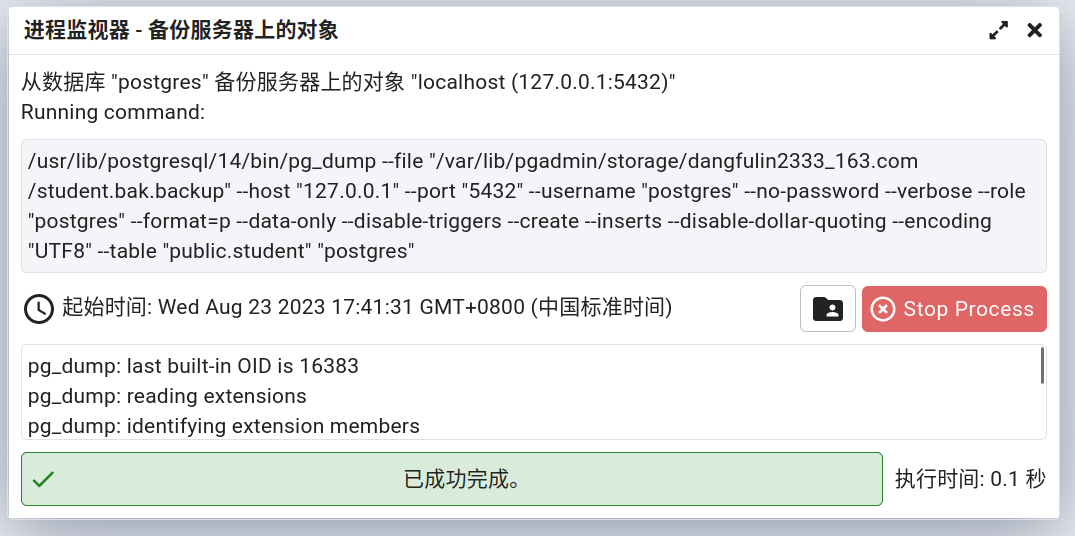
pgadmin4中的备份与恢复
一,postgresql 数据的备份与恢复 (一)数据库备份与恢复 1,备份 windows环境 1> dump 逻辑备份 1,用管理员身份打开power shell 2,切换到本机 postgresql 安装目录下的 bin 目录: PS C…...
内网穿透——搭建私人影音媒体平台
文章目录 1. 前言2. Jellyfin服务网站搭建2.1. Jellyfin下载和安装2.2. Jellyfin网页测试 3.本地网页发布3.1 cpolar的安装和注册3.2 Cpolar云端设置3.3 Cpolar本地设置 4.公网访问测试5. 结语 1. 前言 随着移动智能设备的普及,各种各样的使用需求也被开发出来&…...

使用psql操作PostgreSQL数据库
postgresql的操作和mysql差别较大。。 可以使用 psql 命令行工具或者其他的 PostgreSQL 客户端工具来查看表。如下是使用 psql 命令行工具查看表的方法: 连接到 PostgreSQL 数据库: 如果一个PostgreSQL的连接为 postgresql://用户名:密码127.0.0.1:5432/…...

什么是网络取证(Network Forensics)
企业采用新技术来检查其网络安全是否存在零日漏洞,与立即指示问题的物理层不同,黑客攻击尝试可能会被忽视并变得严重,直到对网络流量有一个整体的可见性。通过实时监控来跟踪其源和目标的流量,以查明问题或潜在问题的根源。 什么…...

农村农产品信息展示网站的设计与实现(论文+源码)_kaic
摘 要 随着软件技术的迅速发展,农产品信息展示的平台越来越多,传统的农产品显示方法将被计算机图形技术取代。这种网站技术主要把农产品的描述、农产品价格、农产品图片等内容,通过计算机网络的开发技术,在互联网上进行展示,然后通过计算机网…...
keepalived+lvs(DR)(四十六)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、作用 二、调度器配置 三、web节点配置 一、作用 使用keepalived解决lvs的单点故障 高可用集群 二、调度器配置 安装keepalived yum install -y k…...

从数据孤岛到企业xPA的演化
“数据孤岛”一直以来是企业在信息化进程中面临的比较头疼的问题,由于数据独立存在于不同部门之中,无法进行相互联动,致使数据库无法兼容,这无形中加大了跨部门合作的沟通成本。在此背景下,一种新兴的规划方法——扩展…...
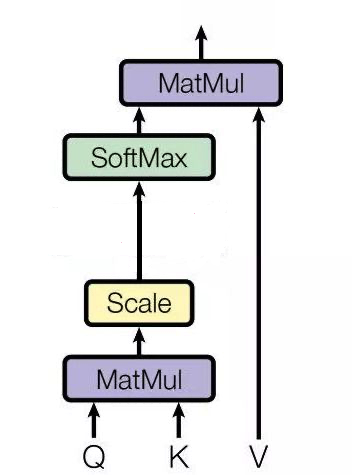
视觉注意力收集
参考博文:神经网络学习小记录64——Pytorch 图像处理中注意力机制的解析与代码详解_pynq 注意力机制_Bubbliiiing的博客-CSDN博客 【计算机视觉】详解 自注意力:Non-local 模块与 Self-attention (视觉注意力机制 (一))_自注意力模块_何处闻韶的博客-CS…...
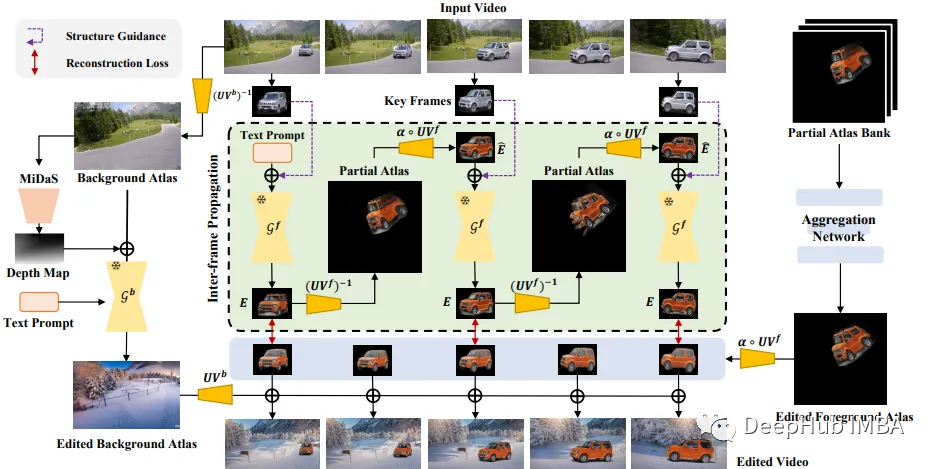
StableVideo:使用Stable Diffusion生成连续无闪烁的视频
使用Stable Diffusion生成视频一直是人们的研究目标,但是我们遇到的最大问题是视频帧和帧之间的闪烁,但是最新的论文则着力解决这个问题。 本文总结了Chai等人的论文《StableVideo: Text-driven consistency -aware Diffusion Video Editing》ÿ…...
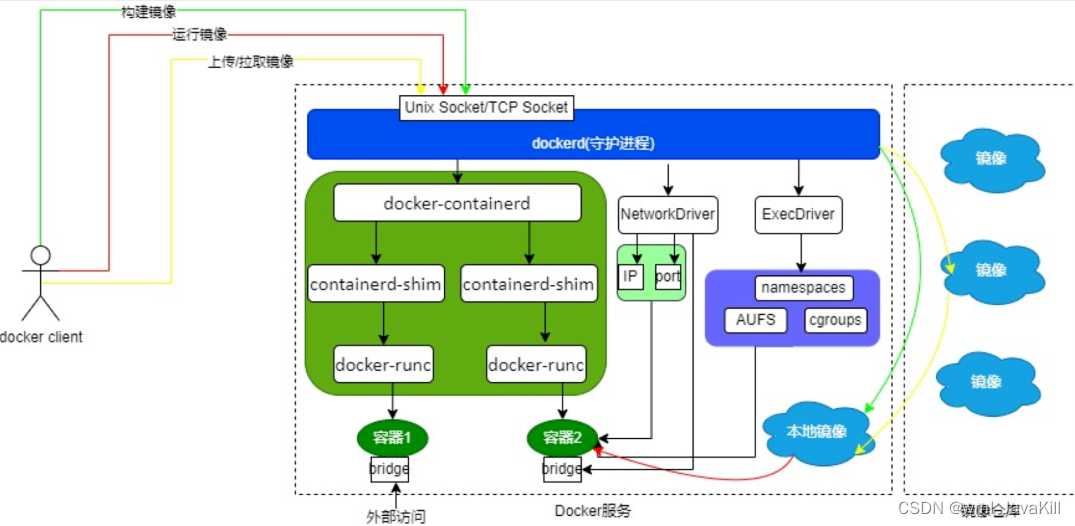
「快学Docker」Docker容器安全性探析
「快学Docker」Docker容器安全性探析 引言容器安全性威胁Docker容器安全性目录容器镜像安全性主机与容器隔离访问控制运行时监控与防御网络安全性Docker容器安全性最佳实践 总结 引言 在当今快速发展的软件开发和部署领域,容器化技术已经成为一种不可或缺的工具。然…...

鲍威尔“放鹰”,美联储或将再加息?
KlipC报道:美联储主席鲍威尔8月25日举行的杰克逊霍尔全球央行年会上表示,尽管过去一年通胀总体持续下行,但住房和服务通胀仍处于高位,鲍威尔也表达了通胀上行风险的担忧,多次表示可能会在适当的情形进一步加息。演讲结…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
