平衡二叉树及其应用详解
平衡二叉树
定义与性质
平衡二叉树(Balanced Binary Tree)是计算机科学中的一种数据结构,它是二叉排序树的一种特殊情况。
平衡二叉树满足以下性质:
左子树和右子树的高度差不超过 1。也就是说,对于任意节点,其左子树和右子树的高度差不超过 1。
左子树和右子树也都是平衡二叉树。
平衡二叉树的定义可以通过递归的方式来定义。一棵高度为 h 的平衡二叉树,必须满足以下两个条件之一:
该树为空,此时高度为 0。
该树的左子树和右子树都是高度为 h-1 的平衡二叉树。
平衡二叉树的定义保证了树中的每个节点的左右子树的高度差不超过 1,从而使得树的高度比较平衡,便于实现各种操作。
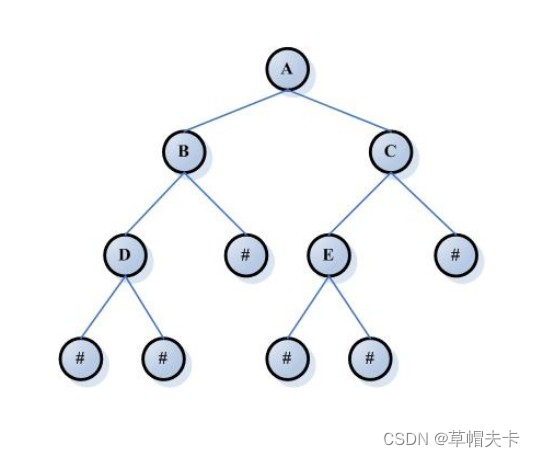
平衡二叉树的应用非常广泛,例如在搜索算法、排序算法、数据结构等领域中都有广泛的应用。由于平衡二叉树的高度比较平衡,因此它具有较好的时间复杂度,特别是对于查找操作,其时间复杂度为 O(logn),其中 n 是树中的节点数。
查找遍历
平衡二叉树的查找遍历有三种基本的方法:前序遍历、中序遍历和后序遍历。
前序遍历(Preorder Traversal):先访问根节点,然后按照先左后右的顺序递归遍历左子树和右子树。
中序遍历(Inorder Traversal):先按照先左后右的顺序递归遍历左子树,然后访问根节点,最后按照先左后右的顺序递归遍历右子树。
后序遍历(Postorder Traversal):先按照先左后右的顺序递归遍历左子树,然后按照先左后右的顺序递归遍历右子树,最后访问根节点。
除了这三种基本的遍历方法,平衡二叉树还有其他的遍历方法,例如层序遍历(Level Order Traversal)、反向遍历(Reverse Traversal)等。不同的遍历方法可以用于不同的应用场景,例如树的打印、树的统计等。
前序遍历
首先,我们需要定义一个平衡二叉树的节点类,包含左右子节点和节点值。然后,实现前序遍历的方法。
以下是平衡二叉树的前序遍历Java代码实现:
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class BinaryTreePreorderTraversal {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val);if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}return result;}
}
这段代码首先定义了一个TreeNode类,用于表示平衡二叉树的节点。然后定义了一个BinaryTreePreorderTraversal类,其中包含一个preorderTraversal方法,用于实现前序遍历。在这个方法中,我们使用了一个栈来辅助遍历,确保遍历的顺序是前序遍历的顺序。
中序遍历
平衡二叉树的中序遍历可以使用递归或迭代的方式实现。以下是使用递归方式实现的代码:
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class BinaryTreeInorderTraversal {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();TreeNode curr = root;while (curr != null || !stack.isEmpty()) {while (curr != null) {stack.push(curr);curr = curr.left;}curr = stack.pop();result.add(curr.val);curr = curr.right;}return result;}
}
这段代码中,我们首先判断根节点是否为空,如果为空则直接返回一个空的结果列表。然后创建一个栈,并将根节点入栈。接下来进入循环,每次从栈中弹出一个节点,将其值加入结果列表中,并将其右子节点(如果存在)入栈。最后返回结果列表即可。
后序遍历
平衡二叉树的后序遍历可以使用递归或迭代的方式实现。以下是使用递归方式实现的代码:
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class BinaryTreePostorderTraversal {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val);if (node.left != null) {stack.push(node.left);}if (node.right != null) {stack.push(node.right);}}return result;}
}
这段代码中,我们首先判断根节点是否为空,如果为空则直接返回一个空的结果列表。然后创建一个栈,并将根节点入栈。接下来进入循环,每次从栈中弹出一个节点,将其值加入结果列表中,并将其左右子节点(如果存在)入栈。最后返回结果列表即可。
插入与删除
平衡二叉树的插入与删除是二叉查找树的重要操作,普通二叉搜索树的操作类似,但是需要通过旋转来保持树的平衡。具体来说,插入或删除一个节点后,需要根据该节点的位置和平衡因子来判断是否需要进行旋转。如果需要进行旋转,则可以分为四种类型:L-L型旋转、L-R型旋转、R-L型旋转和R-R型旋转。这些类型的旋转都有相应的Java代码实现 。
下面是平衡二叉树插入和删除的Java实现:
public class AVLTree {class Node {int key, height;Node left, right;Node(int d) {key = d;height = 1;}}Node root;// 获取节点高度int height(Node N) {if (N == null)return 0;return N.height;}// 获取两个整数的最大值int max(int a, int b) {return (a > b) ? a : b;}// 新建一个节点Node newNode(int key) {Node node = new Node(key);node.left = null;node.right = null;node.height = 1;return node;}// 右旋转Node rightRotate(Node y) {Node x = y.left;Node T2 = x.right;x.right = y;y.left = T2;y.height = max(height(y.left), height(y.right)) + 1;x.height = max(height(x.left), height(x.right)) + 1;return x;}// 左旋转Node leftRotate(Node x) {Node y = x.right;Node T2 = y.left;y.left = x;x.right = T2;x.height = max(height(x.left), height(x.right)) + 1;y.height = max(height(y.left), height(y.right)) + 1;return y;}// 获取平衡因子int getBalance(Node N) {if (N == null)return 0;return height(N.left) - height(N.right);}// 插入节点Node insert(Node node, int key) {if (node == null)return (newNode(key));if (key < node.key)node.left = insert(node.left, key);else if (key > node.key)node.right = insert(node.right, key);else // 相等的键不允许在BST中return node;node.height = 1 + max(height(node.left), height(node.right));int balance = getBalance(node);// 如果节点不平衡,有四种情况需要处理// 左左型旋转if (balance > 1 && key < node.left.key)return rightRotate(node);// 右右型旋转if (balance < -1 && key > node.right.key)return leftRotate(node);// 左右型旋转if (balance > 1 && key > node.left.key) {node.left = leftRotate(node.left);return rightRotate(node);}// 右左型旋转if (balance < -1 && key < node.right.key) {node.right = rightRotate(node.right);return leftRotate(node);}return node;}// 删除节点Node deleteNode(Node root, int key) {if (root == null)return root;if (key < root.key)root.left = deleteNode(root.left, key);else if (key > root.key)root.right = deleteNode(root.right, key);else {if ((root.left == null) || (root.right == null)) {Node temp = null;if (temp == root.left)temp = root.right;elsetemp = root.left;if (temp == null) {temp = root;root = null;} elseroot = temp;} else {Node temp = minValueNode(root.right);root.key = temp.key;root.right = deleteNode(root.right, temp.key);}}if (root == null)return root;root.height = max(height(root.left), height(root.right)) + 1;int balance = getBalance(root);// 如果节点不平衡,有四种情况需要处理// 左左型旋转if (balance > 1 && getBalance(root.left) >= 0)return rightRotate(root);// 右右型旋转if (balance < -1 && getBalance(root.right) <= 0)return leftRotate(root);// 左右型旋转if (balance > 1 && getBalance(root.left) < 0) {root.left = leftRotate(root.left);return rightRotate(root);}// 右左型旋转if (balance < -1 && getBalance(root.right) > 0) {root.right = rightRotate(root.right);return leftRotate(root);}return root;}// 获取最小值节点Node minValueNode(Node node) {Node current = node;while (current.left != null)current = current.left;return current;}
}
复杂度分析
时间复杂度
平衡二叉树的时间复杂度主要取决于插入、删除和查找操作的实现。下面将详细分析这三种操作的时间复杂度。
插入操作:
平衡二叉树的插入操作的时间复杂度为 O(logn),其中 n 是树的节点数量。这是因为插入操作需要在树中找到适当的位置,以保证树的平衡。具体来说,插入操作需要执行以下步骤:
- 将节点插入到树的根节点。
- 如果插入的节点的值比根节点的值小,则将节点插入到根节点的左子树。
- 如果插入的节点的值比根节点的值大,则将节点插入到根节点的右子树。
- 在左子树或右子树中,重复执行步骤 2 和步骤 3,直到找到适当的位置。
在执行插入操作的过程中,最坏情况下需要执行 O(logn)次比较操作,才能找到适当的位置。因此,插入操作的时间复杂度为 O(logn)。
删除操作:
平衡二叉树的删除操作的时间复杂度为 O(logn),其中 n 是树的节点数量。这是因为删除操作需要找到要删除的节点,并在树中进行调整,以保持树的平衡。具体来说,删除操作需要执行以下步骤:
- 找到要删除的节点。
- 如果要删除的节点只有一个孩子节点,则直接将该节点删除,并将该节点的孩子节点替换该节点。
- 如果要删除的节点有两个孩子节点,则需要找到该节点的后继节点,并将该节点的值替换为后继节点的值,然后删除该节点的后继节点。
- 在执行删除操作的过程中,需要对树进行调整,以保持树的平衡。
在执行删除操作的过程中,最坏情况下需要执行 O(logn)次比较操作,才能找到要删除的节点并进行调整。因此,删除操作的时间复杂度为 O(logn)。
查找操作:
平衡二叉树的查找操作的时间复杂度为 O(logn),其中 n 是树的节点数量
空间复杂度
平衡二叉树的空间复杂度主要取决于树的实现方式。下面将详细分析平衡二叉树的空间复杂度。
如果使用数组实现平衡二叉树,则空间复杂度为 O(n),其中 n 是树的节点数量。这是因为数组需要存储树的所有节点,每个节点需要占用一个存储空间。因此,空间复杂度为 O(n)。
如果使用链表实现平衡二叉树,则空间复杂度为 O(n),其中 n 是树的节点数量。这是因为链表需要存储树的所有节点,每个节点需要占用一个存储空间。因此,空间复杂度为 O(n)。
如果使用递归实现平衡二叉树,则空间复杂度为 O(logn),其中 n 是树的节点数量。这是因为递归实现需要使用栈来存储递归调用的上下文,每次递归调用需要占用一个栈帧,因此空间复杂度为 O(logn)。
总的来说,平衡二叉树的空间复杂度取决于树的实现方式。如果使用数组或链表实现平衡二叉树,则空间复杂度为 O(n),其中 n 是树的节点数量。如果使用递归实现平衡二叉树,则空间复杂度为 O(logn),其中 n 是树的节点数量。
应用场景
平衡二叉树的应用场景如下:
- 排序:平衡二叉树可以作为一种排序算法,例如堆排序和快速排序。通过维护一个平衡二叉树,可以快速地对数据进行排序。
- 查找:平衡二叉树可以作为一种查找算法,例如二叉查找树。通过维护一个平衡二叉树,可以快速地在树中查找特定的节点。
- 数据结构:平衡二叉树可以作为一种数据结构,例如红黑树。红黑树是一种特殊的平衡二叉树,它具有以下特点:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色。
- 每个叶子节点(NIL 节点,空节点)是黑色。
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
红黑树在实际应用中非常广泛,例如在操作系统、数据库、图形学等领域中都有广泛的应用。(下一篇将对红黑树做出详细介绍)
相关文章:

平衡二叉树及其应用详解
平衡二叉树 定义与性质 平衡二叉树(Balanced Binary Tree)是计算机科学中的一种数据结构,它是二叉排序树的一种特殊情况。 平衡二叉树满足以下性质: 左子树和右子树的高度差不超过 1。也就是说,对于任意节点&#…...

vue3+ ts ts语法在script写不知道为啥一直报错
在vue3页面中写ts语法 发现识别不了 一直报错 1.出现这种问题的话,首先查看自己写的有没有问题,没有问题的话 2.再查看 script里边有没有写 lang"ts" <script setup lang"ts">解析 setup:是vue3在单文件组件 (SFC) 中使用 composition …...
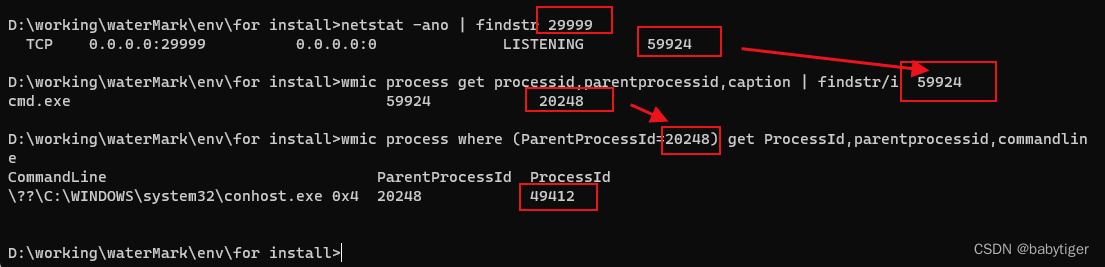
c#写的端口监听,程序退出后,再次运行提示端口占用,且进程不存在
我用c#写了一个监听29999端口,进程结束后再次启动发现端口被占用,但是运行netstat -ano | findstr 29999找到进程ID后,却没有这个进程 经查询这个监听29999进程虽然没了,但是要找到他的父进程,把父进程关闭了才可以,参…...

跨域案例go gf ,请求代理,前端请求后端A转发给多个后端B
跨域案例go gf ,请求代理,前端请求后端A转后端B 案例:从前端请求后端A(路径携带argusx),后端A转发请求到多个不同地区(可一个)后端B(切掉argusx,其他不变进行请求)&…...

9.4 集成功率放大电路
OTL、OCL 和 BTL 电路均有各种不同输出功率和不同电压增益的集成电路。应当注意,在使用 OTL 电路时,需外接输出电容。为了改善频率特性,减小非线性失真,很多电路内部还引入深度负反馈。这里以低频功放为例。 一、集成功率放大电路…...
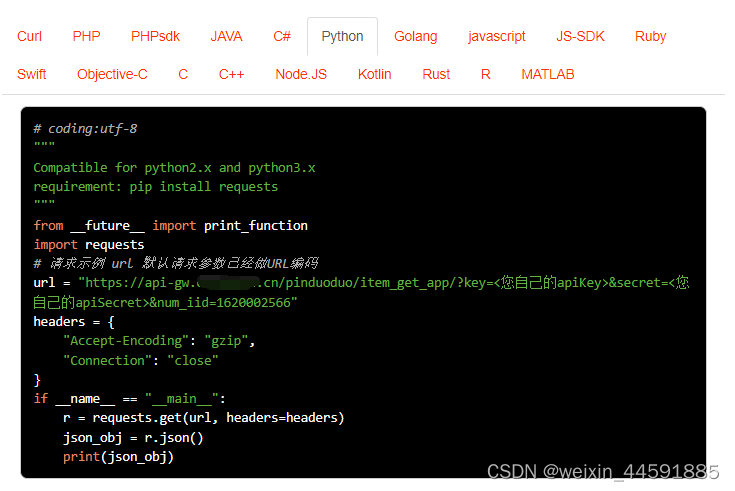
Java“牵手“拼多多商品详情数据、拼多多优惠券信息、拼多多到手价信息获取方法,拼多多API实现批量商品数据抓取示例
拼多多商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取拼多多商品详情数据,您可以通过开放平台的接口或者直接访问拼多多商城的网页来获取商品详情信息。以下是两种常用方法的介绍:…...

亚马逊云科技 re:Inforce 大会云安全合规与技术实践及 Security Jam 大赛,快来报名吧!...
2023年8月31日在北京 亚马逊云科技 re:Inforce 大会 首次登陆中国! 我们期待您的莅临, 并与您一起迎接 AI 时代, 开启全面智能的安全旅程! 在13:00-17:00的 培训与动手实验环节中 云安全合规与技术实践 及 Security Jam 大赛…...

网络安全(黑客技术)学习手册
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...

泡泡玛特回应头部IP营收增速放缓:IP上市时间不固定
8月23日,针对今年上半年头部IP营收增速放缓问题,泡泡玛特(09992.HK)管理层在业绩会上解释称,每个IP上市时间并不固定,单从上半年看同比增长会有偏差,而随着下半年两个新系列的推出,全…...

很干的 Nginx
🎨 前言 本篇文章有些概念性的东西,是结合自己的理解表达出来的,可能有些理解不到位的地方。希望多多指教,谢谢大家。 红包献上 🧧🧧🧧🧧🧧🧧🧧…...
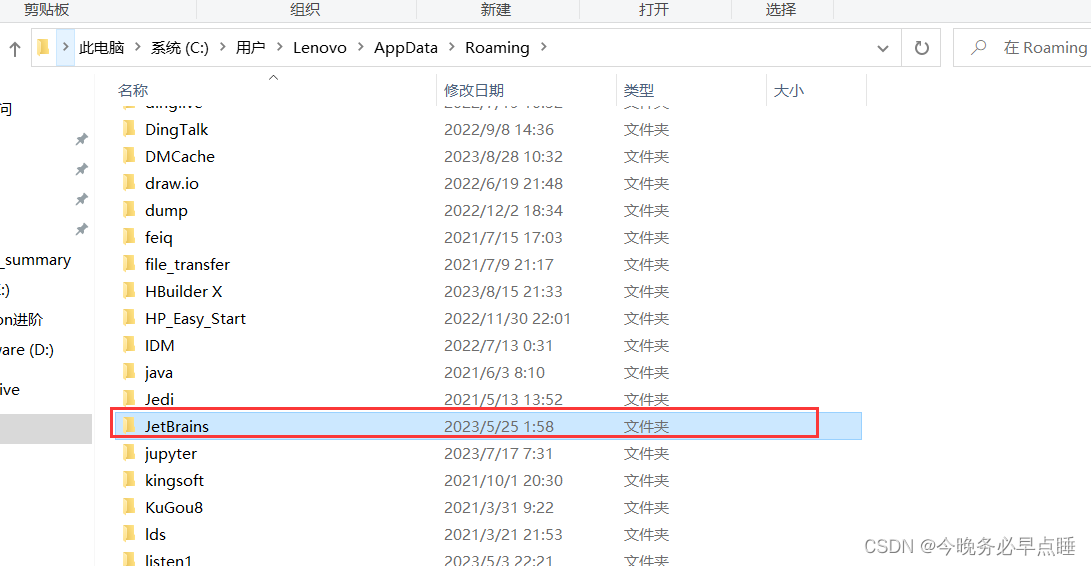
【已解决】pycharm突然双击无法打开,重启电脑也不管用
1.问题: pycharm突然双击无法打开,重启电脑也不管用 2.解决 2.1 方法一(修改Roaming) 1.找到C盘对应路径下的pycharm版本 2. 用记事本打开文件类型为VMOPTIONS文件 3. 修改或删除最后一行的映射路径 4.保存退出 2.2 方法二…...
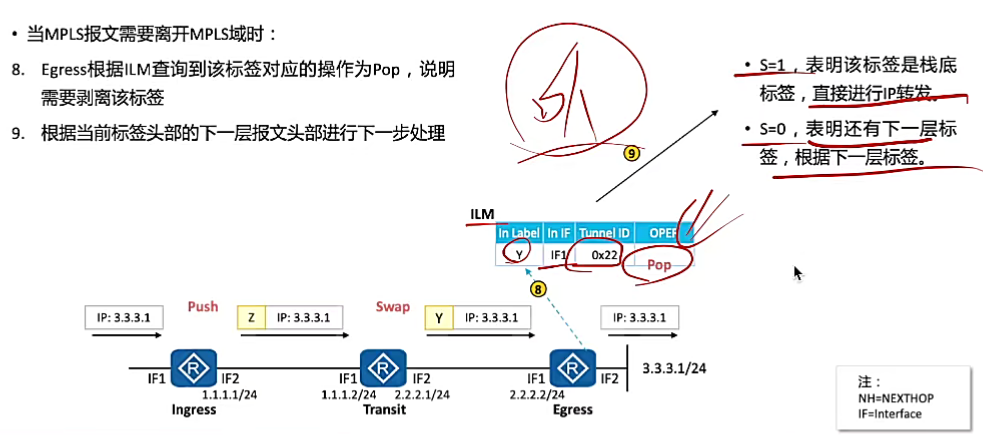
【HCIP】15.MPLS基础
多协议标签交换 MPLS位于TCP/IP协议栈中的数据链路层和网络层之间,可以向所有网络层提供服务。 通过在数据链路层和网络层之间增加额外的MPLS头部,基于MPLS头部实现数据快速转发。 术语 MPLS域(MPLS Domain):一系列…...

热烈祝贺重庆融能成功入选航天系统采购供应商库
经过航天系统采购平台的严审,重庆融能机电设备股份有限公司成功入选中国航天系统采购供应商库。航天系统采购平台是航天系统内企业采购专用平台,服务航天全球范围千亿采购需求,目前,已有华为、三一重工、格力电器、科大讯飞等企业…...

隧道vs免费爬虫ip:为何要选择隧道爬虫ip?
在网络爬虫的世界中,爬虫ip是一项关键技术,它可以帮助我们隐藏身份、突破限制、提高抓取效率。但是,在选择爬虫ip时,我们常常会面对隧道爬虫ip和免费爬虫ip之间的抉择。在本文中,我们将探讨隧道爬虫ip相对于免费爬虫ip…...
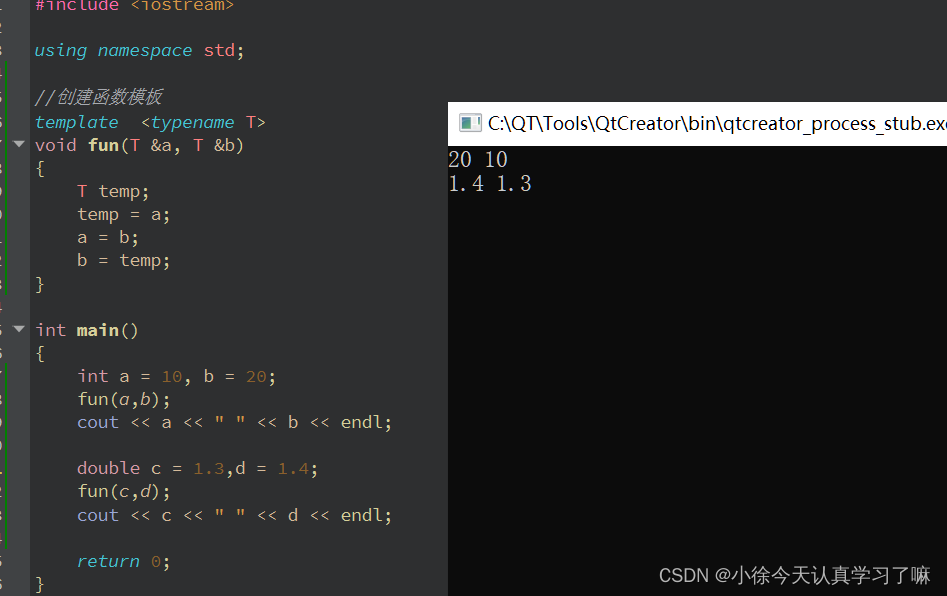
C++day6(多态实现动物园的讲解员和动物表演的相关介绍、用函数模板实现不同数据类型的交换功能)
1.比喻:动物园的讲解员和动物表演 想象一下你去了一家动物园,看到了许多不同种类的动物,如狮子、大象、猴子等。现在,动物园里有一位讲解员,他会为每种动物表演做简单的介绍。 在这个场景中,我们可以将动…...

多线程学习之生产者和消费者与阻塞队列的关系
生产者和消费者 概述: 生产者消费者问题,实际上主要是包含了两类线程: 生产者线程用于生产数据消费者线程用于消费数据 生产者和消费者之间通常会采用一个共享的数据区域,这样就可以将生产者和消费者进行解耦, 两…...

JAVA语言代入电商平台api接口拼多多根据关键词获取商品列表示例
拼多多根据关键词获取商品接口的意义; 实现商品搜索:通过关键词搜索商品API接口,电商平台可以为消费者提供一个简单、快捷的商品搜索功能。用户只需输入关键词,就可以得到与该关键词相关的商品列表。 提供便捷的商品搜索服务&…...
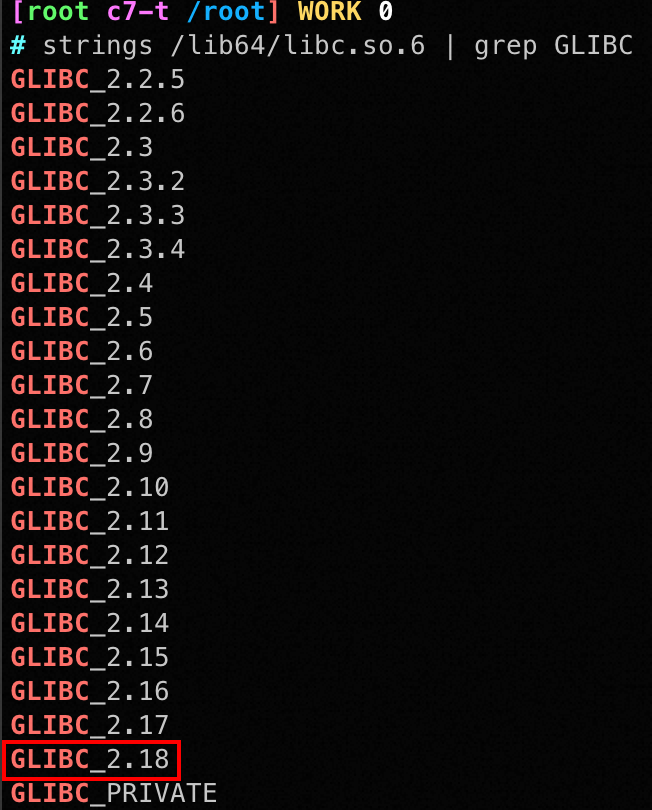
Centos7更新glibc2.18
Centos7更新glibc2.18 查看glibc版本下载解压glibc2.18编译安装结果验证 查看glibc版本 # 查看glibc版本 ldd --version下载解压glibc2.18 参考: https://blog.csdn.net/qq_39295044/article/details/86685789 https://blog.csdn.net/myhes/article/details/106923039 # 下载…...
QT初学者该安装qt creator哪个版本?
对于Qt初学者,建议安装最新版本的Qt Creator。Qt Creator是Qt官方提供的集成开发环境(IDE),用于开发Qt应用程序。每个Qt版本都会配套提供对应的Qt Creator版本,确保兼容性和稳定性。同时,选择合适的Qt版本也…...

VR智慧校园资中控管理平台综合提升了课堂教学质量
随着越来越多高校在课堂中引进VR虚拟仿真实训系统,为了方便老师对全班同学进行高效率地管理,VR中控平台应运而生。下面为您详细介绍VR中控平台在课堂教学中的应用优势。 VR中控系统安装在教师总控端,融合了课件、视频、3D动画等丰富的教学资源…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
