LeetCode538. 把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树
文章目录
- [538. 把二叉搜索树转换为累加树](https://leetcode.cn/problems/convert-bst-to-greater-tree/)
- 一、题目
- 二、题解
- 方法一:递归(中序遍历与节点更新)
- 方法二:反向中序遍历与累加更新:更简洁的解法
- 方法三:迭代(反向中序遍历)
一、题目
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
示例 1:
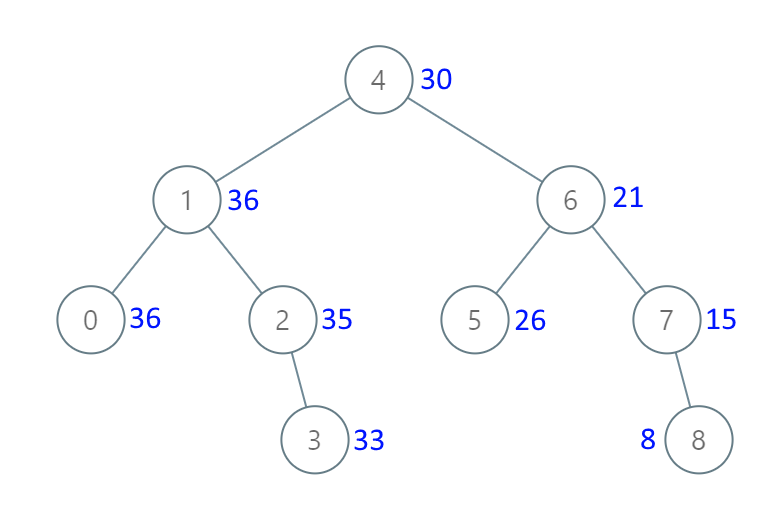
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
二、题解
方法一:递归(中序遍历与节点更新)
针对这个问题,我们可以考虑通过中序遍历来获取有序的节点值,然后从大到小更新节点的值,以满足累加树的要求。
算法思路
-
创建一个空的向量
array用于存储中序遍历得到的有序节点值。 -
执行中序遍历函数
traversal_vec(root, array),该函数会将二叉搜索树的节点值按照从小到大的顺序存储在array中。 -
从
array的倒数第二个元素开始,将每个元素与其后一个元素相加,以便得到累加和。这一步保证了在累加树中,每个节点的值等于原树中大于或等于该节点值的所有节点值之和。 -
执行函数
traversal_res(root, array),该函数会将更新后的累加和值赋给二叉搜索树的每个节点。 -
返回更新后的二叉搜索树。
具体实现
以下是对每个步骤的详细实现:
class Solution {
public:int i = 0;// 中序遍历获取有序节点值并存储在array中void traversal_vec(TreeNode *root, vector<int> &array){if(root == nullptr) return;traversal_vec(root->left, array);array.push_back(root->val);traversal_vec(root->right, array);}// 更新节点值为累加和void traversal_res(TreeNode *root, vector<int>& array){if(root == nullptr) return;traversal_res(root->left, array);root->val = array[i++];traversal_res(root->right, array);}TreeNode* convertBST(TreeNode* root) {if(root == nullptr) return nullptr;vector<int> array;// 获取有序节点值traversal_vec(root, array);// 计算累加和for(int j = array.size() - 2; j >= 0; j--){array[j] += array[j+1];}// 更新节点值为累加和traversal_res(root, array);return root;}
};
或者将i作为参数传入traversal_res()也行:
class Solution {
public:void traversal_vec(TreeNode *root, vector<int> &array) {if (root == nullptr) return;traversal_vec(root->left, array);array.push_back(root->val);traversal_vec(root->right, array);}int traversal_res(TreeNode *root, int i, const vector<int> &array) {if (root == nullptr) return i;i = traversal_res(root->left, i, array);root->val = array[i];i++;i = traversal_res(root->right, i, array);return i;}TreeNode* convertBST(TreeNode* root) {if (root == nullptr) return nullptr;vector<int> array;traversal_vec(root, array);for (int j = array.size() - 2; j >= 0; j--) {array[j] += array[j + 1];}traversal_res(root, 0, array);return root;}
};算法分析
-
时间复杂度:算法的时间复杂度主要由两个部分构成:中序遍历和更新节点值。中序遍历需要访问每个节点一次,而更新节点值也需要访问每个节点一次。因此,算法的时间复杂度为 O(N),其中 N 是节点的数量。
-
空间复杂度:算法的空间复杂度主要由中序遍历时存储节点值的数组
array所占用的空间。在最坏的情况下,数组的大小为 N,因此空间复杂度为 O(N)。除此之外,递归调用栈也会占用一些空间,但是在二叉搜索树的情况下,递归调用栈的最大深度不会超过树的高度,因此额外空间的使用不会超过 O(log N)。
方法二:反向中序遍历与累加更新:更简洁的解法
算法思路
这个算法采用了一种不同的方法来实现二叉搜索树到累加树的转换。通过反向中序遍历(从右子树到左子树),我们可以更方便地得到大于当前节点值的节点值之和,然后直接更新节点值,从而获得累加树。
具体实现
class Solution {
public:// 反向中序遍历并更新节点值void convertBSTHelper(TreeNode* root, int& sum) {if(root == nullptr) return;convertBSTHelper(root->right, sum); // 先处理右子树sum += root->val; // 更新累加和root->val = sum; // 更新节点值convertBSTHelper(root->left, sum); // 处理左子树}TreeNode* convertBST(TreeNode* root) {if(root == nullptr) return nullptr;int sum = 0;convertBSTHelper(root, sum);return root;}
};
算法分析
- 时间复杂度:算法的时间复杂度主要由中序遍历和更新节点值组成。每个节点都会被访问一次且只访问一次,因此时间复杂度为 O(N),其中 N 是节点的数量。
- 空间复杂度:算法的空间复杂度由递归调用栈所占用的空间决定。在二叉搜索树的情况下,递归调用栈的最大深度不会超过树的高度,因此额外空间的使用不会超过 O(log N)。
方法三:迭代(反向中序遍历)
算法思路
这个算法采用了反向中序遍历的方式,通过栈来实现,来构建累加树。遍历的过程中,我们从最大值开始,逐步向较小值移动,同时将大于等于当前节点值的所有节点值累加起来,然后将该累加值赋予当前节点,最终构建出累加树。
具体实现
class Solution {
private:int previousValue; // 记录前一个节点的值// 反向中序遍历并更新节点值void reverseInorderTraversal(TreeNode* root) {stack<TreeNode*> nodeStack;TreeNode* current = root;while (current != nullptr || !nodeStack.empty()) {if (current != nullptr) {nodeStack.push(current);current = current->right; // 右子树} else {current = nodeStack.top(); // 弹出栈顶节点nodeStack.pop();// 更新节点值current->val += previousValue;previousValue = current->val;current = current->left; // 左子树}}}public:TreeNode* convertBST(TreeNode* root) {previousValue = 0; // 初始化前一个节点的值reverseInorderTraversal(root); // 反向中序遍历更新节点值return root;}
};
算法分析
-
时间复杂度:算法的时间复杂度主要由反向中序遍历过程构成。每个节点会被访问一次且只访问一次,因此时间复杂度为 O(N),其中 N 是节点的数量。
-
空间复杂度:算法的空间复杂度由栈所占用的空间决定。在最坏情况下,栈的大小可能达到树的高度,即 O(log N)。
相关文章:

LeetCode538. 把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树 文章目录 [538. 把二叉搜索树转换为累加树](https://leetcode.cn/problems/convert-bst-to-greater-tree/)一、题目二、题解方法一:递归(中序遍历与节点更新)方法二:反向中序遍历与累加更新&#x…...

TP6 使用闭合语句查询多个or的模型语句
例子:查询出在单位表中所有的小学,初中和高中;其中school_period保存的就是学段数据$where []; $where[] function ($query) {$query->where(school_period, like, %小学%)->whereOr(school_period, like, %初中%)->whereOr(schoo…...

浅析Linux SCSI子系统:设备管理
文章目录 概述设备管理数据结构scsi_host_template:SCSI主机适配器模板scsi_host:SCSI主机适配器主机适配器支持DIF scsi_target:SCSI目标节点scsi_device:SCSI设备 添加主机适配器构建sysfs目录 添加SCSI设备挂载LunIO请求队列初…...
爬虫逆向实战(二十五)--某矿采购公告
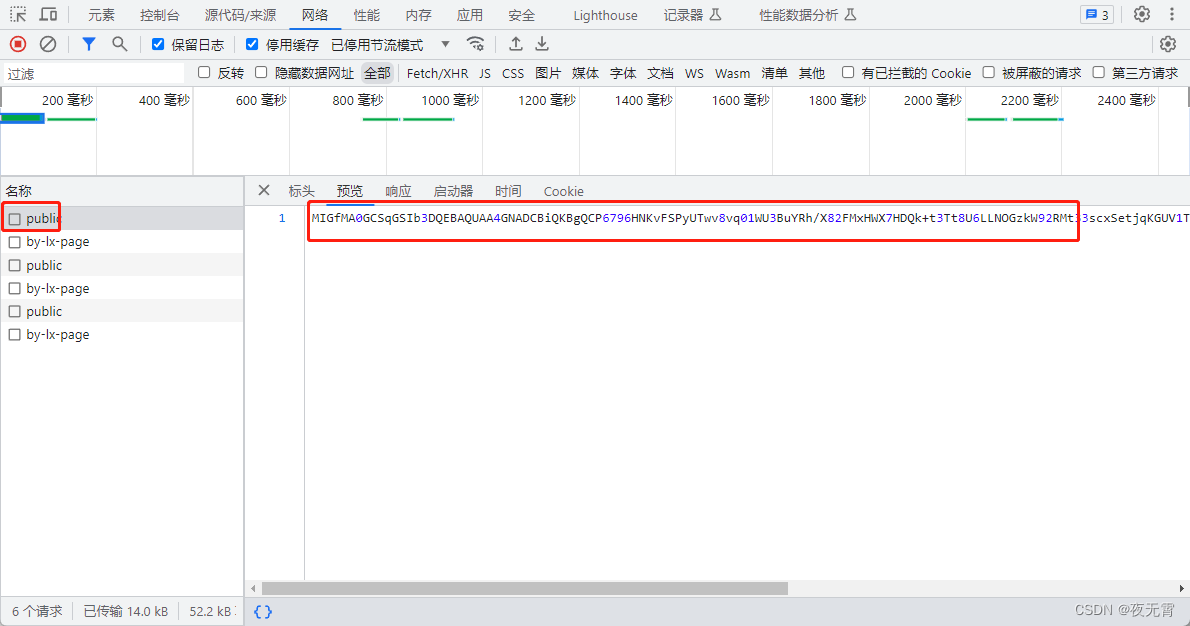
一、数据接口分析 主页地址:某矿 1、抓包 通过抓包可以发现数据接口是cgxj/by-lx-page 2、判断是否有加密参数 请求参数是否加密? 通过查看“载荷”模块可以发现有一个param的加密参数 请求头是否加密? 无响应是否加密? 无c…...

DPLL 算法之分裂策略
前言 DPLL算法确实是基于树(或二叉树)的回溯搜索算法,它用于解决布尔可满足性问题(SAT问题)。下面我会分析您提到的DPLL算法中的分裂策略,以及它是如何在搜索过程中起作用的。 DPLL算法中的分裂策略是用于在…...
Jmeter+ServerAgent
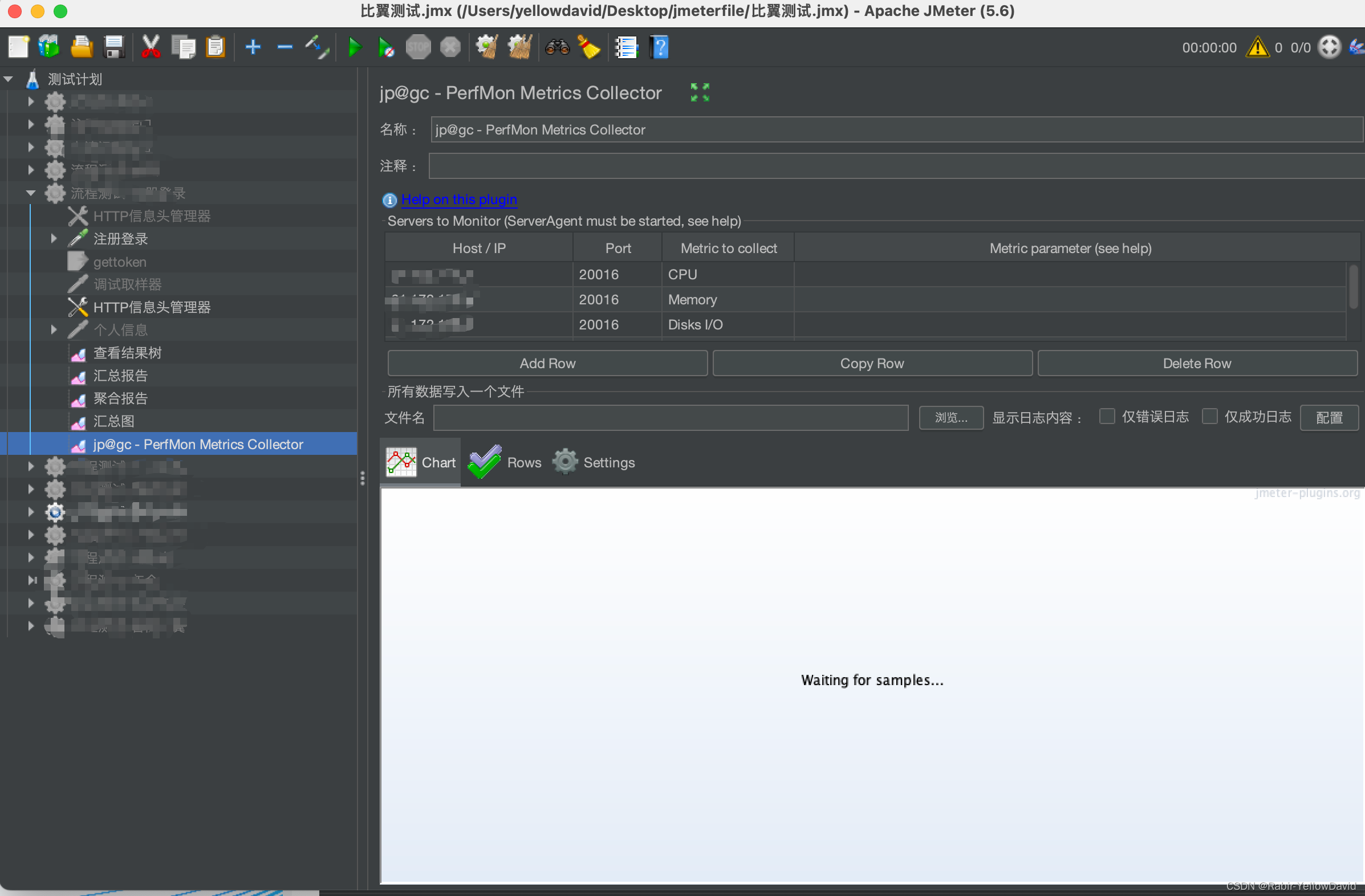
一、Jmeter 下载 https://jmeter.apache.org/download_jmeter.cgi选择Binaries二进制下载 apache-jmeter-5.6.2.tgz 修改配置文件 jmeter下的bin目录,打开jmeter.properties 文件 languagezh_CN启动命令 cd apache-jmeter-5.6/bin sh jmeter二、ServerAgent 监…...

打破数据孤岛!时序数据库 TDengine 与创意物联感知平台完成兼容性互认
新型物联网实现良好建设的第一要务就是打破信息孤岛,将数据汇聚在平台统一处理,实现数据共享,放大物联终端的行业价值,实现系统开放性,以此营造丰富的行业应用环境。在此背景下,物联感知平台应运而生&#…...
ubuntu22安装和部署Kettle8.2
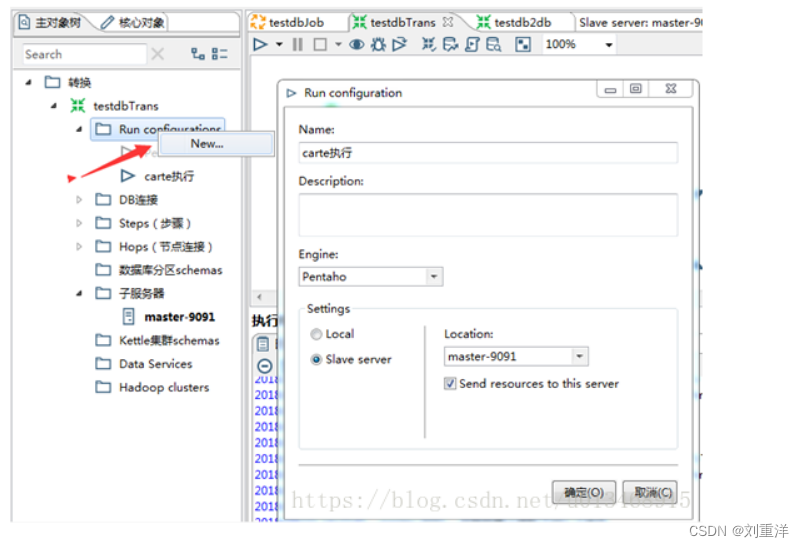
前提 kettle是纯java编写的etl开源工具,目前kettle7和kettle8都需要java8或者以上才能正常运行。所以运行kettle前先检查java环境是否正确配置,java版本是否是8或者以上。 kettle安装 1、创建kettle目录,并将kettle的zip包解压到kettle目…...

修复 Ubuntu Linux 中的“找不到命令‘python’”错误
在ubuntu 22.04版本中使用 callstack backtrace.txt 回溯错误点是碰到了该问题。 参考文章:链接 ubuntu22.04版本中默认只安装了python3版本 查看python各个版本安装情况,在终端输入命令: type python python2 python3如果安装了对应的版本…...
【业务功能篇86】微服务-springcloud-系统性能压力测试-jmeter-性能优化-JVM参数调优
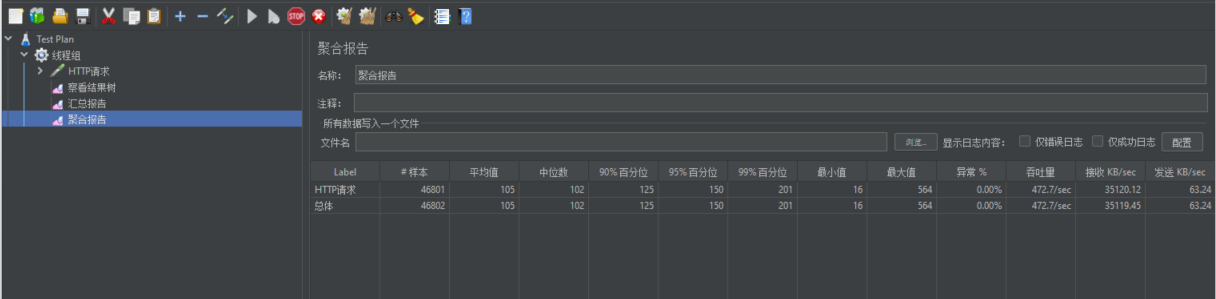
系统性能压力测试 一、压力测试 压力测试是给软件不断加压,强制其在极限的情况下运行,观察它可以运行到何种程度,从而发现性能缺陷,是通过搭建与实际环境相似的测试环境,通过测试程序在同一时间内或某一段时间内&…...

mysql的登录与退出
mysql是c/s架构,意味着同时要有客户端和服务端 1 找到客户端。mysql.exe的安装目录 打开命令行 2 输入对应的服务器的ip,如果是本地,就是Localhost,如果是远程服务器,那就输入对应ip/域名。并且指定mysql监听的端口 …...
SOLIDWORKS工程图转DWG图层映射技巧
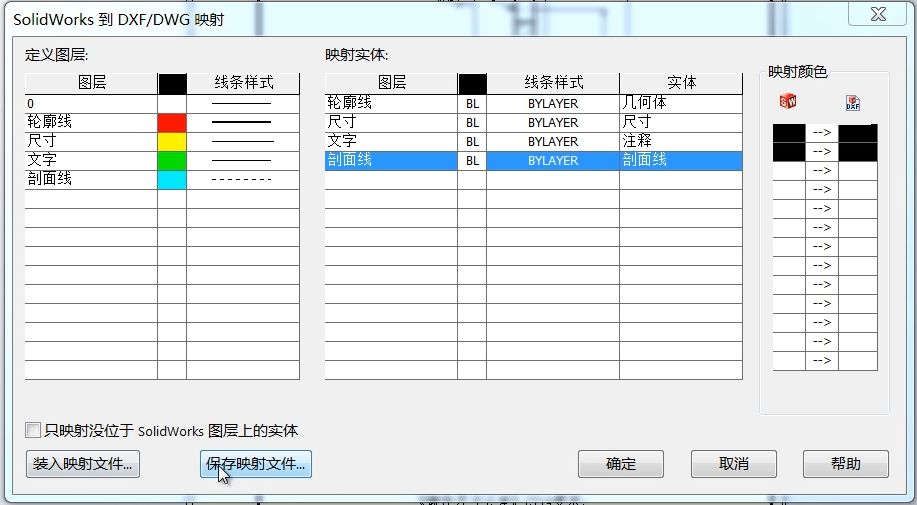
DWG格式的图纸在工程制图中有着非常重要的地位,工程实践中常常就需要将SOLIDWORKS工程图进行转换。对于两者之间数据衔接的妥善处理,是提升工作效率的有效手段。基于此目的,本次我们将介绍数据衔接的一个有效解决方案:图层数据的映…...
PMAC与Modbus主站进行Modbus Tcp通讯
PMAC与Modbus主站进行Modbus Tcp通讯 创建modbus通讯参数 在项目的PMAC Script Language\Global Includes下创建一个名为00_Modbus_Para.pmh的pmh文件。 Modbus[0].Config.ServerPort 0 Modbus[0].Config.ConnectTimeOut 6000 Modbus[0].Config.SendRecvTimeOut 0 Modbu…...
MyBatis分页插件PageHelper的使用及MyBatis的特殊符号---详细介绍
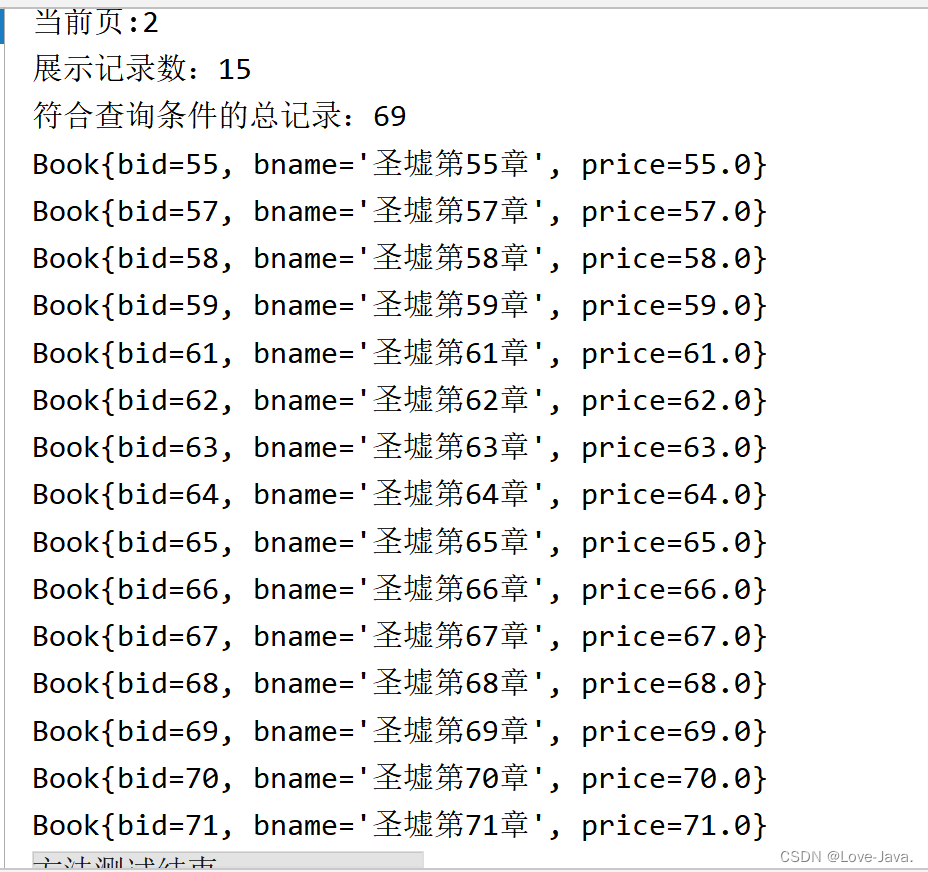
一,分页的概念 分页是一种将大量数据或内容分割成多个页面以便逐页显示的方式。在分页中,数据被分割成一定数量的页,每页显示一部分数据或内容,用户可以通过翻页或跳分页是一种将大量数据或内容分割成多个页面以便逐页显示的方式。…...

Qt(C++)计算一段程序执行经过的时间
一、前言 在许多应用程序和系统中,需要对经过的时间进行计算和记录。例如 可能想要测量某个操作的执行时间,或者记录一个过程中经过的时间以进行性能分析。在这些场景下,准确地计时是非常重要的。 Qt提供了一个功能强大的计时器类QElapsedTimer,可以方便地记录经过的时间…...
UnionTech OS(统信桌面操作系统)安装 g++ 和 cmake
文章目录 前言一、debian 10简介二、安装 g三、安装cmake参考资料 前言 统信桌面操作系统支持x86、龙芯、申威、鲲鹏、飞腾、兆芯等国产CPU平台,基于debian 10.x 的稳定版本,长期维护的统一内核版本(4.19)。 一、debian 10简介 Debian 10 是一款广泛使…...
php_webshell免杀--从0改造你的AntSword
0x00 前言: 为什么会有改造蚁剑的想法,之前看到有做冰蝎的流量加密,来看到绕过waf,改造一些弱特征,通过流量转换,跳过密钥交互。 但是,冰蝎需要反编译去改造源码,再进行修复bug&am…...
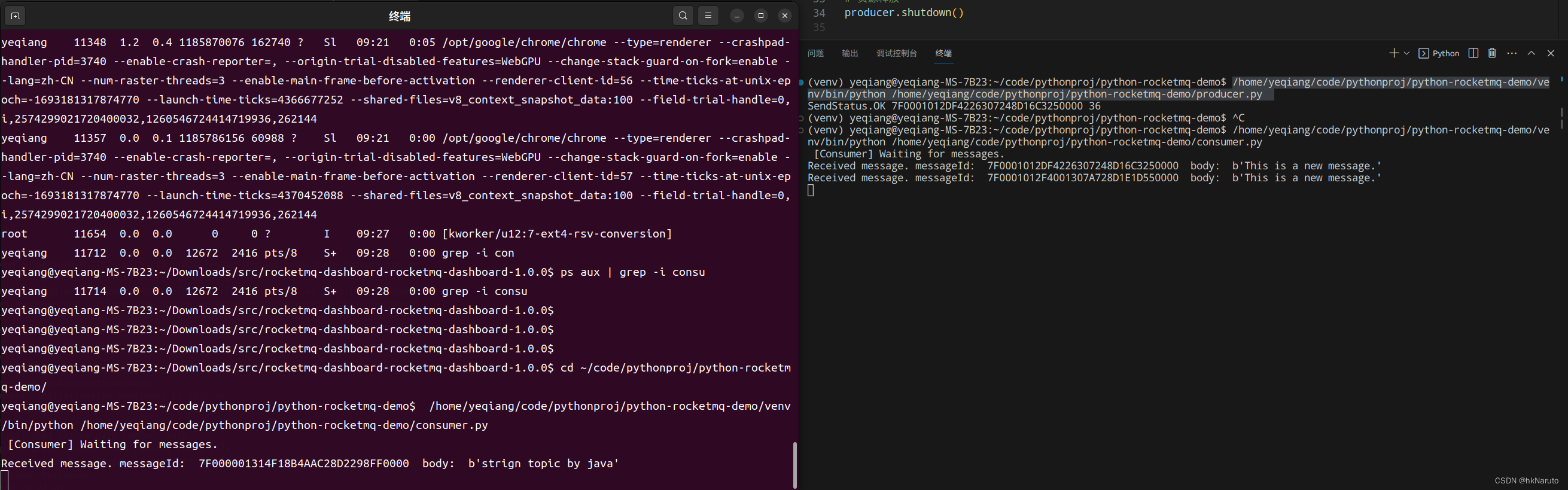
RocketMQ mqadmin java springboot python 调用笔记
命令 mqadmin命令列表 yeqiangyeqiang-MS-7B23:/opt/rocketmq-all-5.1.3-bin-release$ sh bin/mqadmin The most commonly used mqadmin commands are:updateTopic Update or create topicdeleteTopic Delete topic from broker and NameServer.…...

Java aspose 将HTML导出成Excel文件
1.需求 有一批表格的html文件,需要将这些表格导出成excel文件 2.代码 使用第三方库 aspose ByteArrayInputStream htmlIs new ByteArrayInputStream(htmlBuilder.toString().getBytes()); // 将html字符串构建成输入流 LoadOptions lo new LoadOptions(LoadFo…...

原生微信小程序 动态(横向,纵向)公告(广告)栏
先看一下动态效果 Y轴滚动公告的原理是swiper组件在页面中的Y轴滚动,属性vertical,其余属性也设置一下autoplay circular interval"3000" X轴滚动的原理是,利用动画效果,将内容从右往左过渡过去 wxml: &l…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
