已知两地经纬度,计算两地直线距离
文章目录
- 1 原理公式
- 2 代码实现
- 2.1 JavaScript
- 2.2 C++
- 2.3 Python
- 2.4 MATLAB
1 原理公式
在地球上,计算两点之间的直线距离通常使用地理坐标系(例如WGS84)。计算两地直线距离的公式是根据经纬度之间的大圆距离(Great Circle Distance)来计算的。该公式基于球面三角学,常用的公式是 H a v e r s i n e Haversine Haversine 公式。
形式一:
d l o n = l o n 2 − l o n 1 d_{lon} = lon_2 - lon_1 dlon=lon2−lon1
d l a t = l a t 2 − l a t 1 d_{lat} = lat_2 - lat_1 dlat=lat2−lat1
a = s i n 2 ( d l a t / 2 ) + c o s ( l a t 1 ) ∗ c o s ( l a t 2 ) ∗ s i n 2 ( d l o n / 2 ) a = sin²(d_{lat}/2) + cos(lat_1) * cos(lat_2) * sin²(d_{lon}/2) a=sin2(dlat/2)+cos(lat1)∗cos(lat2)∗sin2(dlon/2)
c = 2 ∗ a t a n 2 ( a , ( 1 − a ) ) c = 2 * atan^2(\sqrt{a}, \sqrt{(1-a)}) c=2∗atan2(a,(1−a))
d = R ∗ c d = R * c d=R∗c
形式二:
d = R ∗ a c o s ( s i n ( l o n 1 ) ∗ s i n ( l o n 2 ) + c o s ( l o n 1 ) ∗ c o s ( l o n 2 ) ∗ c o s ( l a t 2 − l a t 1 ) ) d = R*acos(sin(lon_1)*sin(lon_2) + cos(lon_1)*cos(lon_2)*cos(lat_2-lat_1)) d=R∗acos(sin(lon1)∗sin(lon2)+cos(lon1)∗cos(lon2)∗cos(lat2−lat1))
其中:
- R R R 是地球的半径,约为6371千米。

请注意,这个公式假设地球是一个完美的球形。实际上,地球的形状更像一个椭球,因此使用更精确的地理信息系统(GIS)软件或库(如proj.4或GeographicLib)可能会得到更准确的结果。
此外,经纬度通常以度为单位,但上述公式中的角度应被视为弧度。如果经纬度是以度数形式给出的,需要将其转换为弧度。可以通过将度数乘以π/180并取整数部分得到弧度值。例如, 30 ° 30° 30°转换为弧度为 π / 180 ∗ 30 π/180*30 π/180∗30。
2 代码实现
2.1 JavaScript
function calculateDistance(lat1, lon1, lat2, lon2) {const R = 6371; // 地球半径,单位为千米const rad = (angle) => angle * Math.PI / 180; // 将角度转换为弧度const lat1Rad = rad(lat1);const lon1Rad = rad(lon1);const lat2Rad = rad(lat2);const lon2Rad = rad(lon2);const dLat = lat2Rad - lat1Rad;const dLon = lon2Rad - lon1Rad;const a = Math.sin(dLat / 2) * Math.sin(dLat / 2) +Math.cos(lat1Rad) * Math.cos(lat2Rad) *Math.sin(dLon / 2) * Math.sin(dLon / 2);const c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a));const distance = R * c; // 返回单位为千米的距离return distance;
}// 示例用法
const lat1 = 39.9087; // 北京的经纬度
const lon1 = 116.4074;
const lat2 = 31.2304; // 上海的经纬度
const lon2 = 121.4737;const distance = calculateDistance(lat1, lon1, lat2, lon2);
console.log(distance); // 输出直线距离(单位:千米)
2.2 C++
#include <cmath>
#include <iostream>// 计算两个经纬度之间的距离(单位:千米)
double calculateDistance(double lat1, double lon1, double lat2, double lon2) {const double R = 6371; // 地球半径,单位为千米// 将经纬度转换为弧度double lat1Rad = std::atan(std::tan(lat1 * (M_PI / 180)) * std::cos(lon1 * (M_PI / 180)));double lon1Rad = lon1 * (M_PI / 180);double lat2Rad = std::atan(std::tan(lat2 * (M_PI / 180)) * std::cos(lon2 * (M_PI / 180)));double lon2Rad = lon2 * (M_PI / 180);// 计算两个经纬度之间的弧度差double dLat = lat2Rad - lat1Rad;double dLon = lon2Rad - lon1Rad;// 根据球面三角法公式计算距离double a = std::sin(dLat / 2) * std::sin(dLat / 2) +std::cos(lat1Rad) * std::cos(lat2Rad) *std::sin(dLon / 2) * std::sin(dLon / 2);double c = 2 * std::atan2(std::sqrt(a), std::sqrt(1 - a));// 返回距离return R * c;
}// 示例用法
int main() {double lat1 = 39.9087; // 北京的经纬度double lon1 = 116.4074;double lat2 = 31.2304; // 上海的经纬度double lon2 = 121.4737;double distance = calculateDistance(lat1, lon1, lat2, lon2);std::cout << "距离:" << distance << " 千米" << std::endl;return 0;
}
请注意,此代码使用了C++标准库中的数学函数和常量。此外,将经纬度转换为弧度的方法需要使用std::atan和std::tan函数。
2.3 Python
import mathdef calculate_distance(lat1, lon1, lat2, lon2):R = 6371 # 地球半径,单位为千米rad = lambda angle: angle * math.pi / 180 # 将角度转换为弧度lat1_rad = rad(lat1)lon1_rad = rad(lon1)lat2_rad = rad(lat2)lon2_rad = rad(lon2)dLat = lat2_rad - lat1_raddLon = lon2_rad - lon1_rada = math.sin(dLat / 2) ** 2 + math.cos(lat1_rad) * math.cos(lat2_rad) * math.sin(dLon / 2) ** 2c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))distance = R * c # 返回单位为千米的距离return distance# 示例用法
lat1 = 39.9087 # 北京的经纬度
lon1 = 116.4074
lat2 = 31.2304 # 上海的经纬度
lon2 = 121.4737distance = calculate_distance(lat1, lon1, lat2, lon2)
print(distance) # 输出直线距离(单位:千米)
请注意,由于Python和JavaScript之间的一些语法差异,需要使用math模块来进行数学计算。另外,由于Python中没有lambda函数的功能,因此需要使用普通的函数定义来代替。
2.4 MATLAB
function distance = calculateDistance(lat1, lon1, lat2, lon2)const R = 6371; % 地球半径,单位为千米lat1Rad = rad(lat1);lon1Rad = rad(lon1);lat2Rad = rad(lat2);lon2Rad = rad(lon2);dLat = lat2Rad - lat1Rad;dLon = lon2Rad - lon1Rad;a = sin(dLat / 2) .^ 2 + cos(lat1Rad) .* cos(lat2Rad) .* sin(dLon / 2) .^ 2;c = 2 * atan2(sqrt(a), sqrt(1 - a));distance = R * c; % 返回单位为千米的距离
end% 示例用法
lat1 = 39.9087; % 北京的经纬度
lon1 = 116.4074;
lat2 = 31.2304; % 上海的经纬度
lon2 = 121.4737;distance = calculateDistance(lat1, lon1, lat2, lon2);
disp(distance); % 输出直线距离(单位:千米)
请注意,MATLAB中的函数定义以function开头,输入参数以逗号分隔,输出结果使用变量名返回。此外,MATLAB中用.*表示元素之间的相乘,而^表示乘方。最后,使用disp函数输出结果。
相关文章:

已知两地经纬度,计算两地直线距离
文章目录 1 原理公式2 代码实现2.1 JavaScript2.2 C2.3 Python2.4 MATLAB 1 原理公式 在地球上,计算两点之间的直线距离通常使用地理坐标系(例如WGS84)。计算两地直线距离的公式是根据经纬度之间的大圆距离(Great Circle Distanc…...

我想开通期权?如何开通期权账户?
场内期权的合约由交易所统一标准化定制,大家面对的同一个合约对应的价格都是一致的,比较公开透明,期权开户当天不能交易的,期权开户需要满足20日日均50万及半年交易经验即可操作,下文科普我想开通期权?如何…...

ChatGPT对软件测试的影响
ChatGPT 是一个经过预训练的 AI 语言模型,可以通过聊天的方式回答问题,或者与人闲聊。它能处理的是文本类的信息,输出也只能是文字。它从我们输入的信息中获取上下文,结合它被训练的大模型,进行分析总结,给…...
minion在ubuntu上的搭建步骤
在Ubuntu上搭建MinIO可以按照以下步骤进行: 下载MinIO服务器二进制文件: 通过浏览器访问 https://min.io/download 或使用以下命令获取最新的MinIO二进制文件:wget https://dl.min.io/server/minio/release/linux-amd64/minio赋予二进制文件…...
Leetcode刷题笔记--Hot31-40
1--颜色分类(75) 主要思路: 快排 #include <iostream> #include <vector>class Solution { public:void sortColors(std::vector<int>& nums) {quicksort(nums, 0, nums.size()-1);}void quicksort(std::vector<int…...
【Python】环境配置,【Pytorch】GPU版本安装
总结: 使用conda新建切换环境,然后使用pip安装卸载包 【python】pip conda_conda list没有pytorch_myaijarvis的博客-CSDN博客 pip换源 https://blog.csdn.net/maotenghua/article/details/104188086 在当前用户目录下创建pip目录,即C:\U…...
)
BEVFusion复现 (Ubuntu RTX3090)
https://github.com/ADLab-AutoDrive/BEVFusion 1.环境安装 我的机器是RTX3090,CUDA11.1 1.创建虚拟环境 conda create -n bevfusion python3.8.3 2.安装PyTorch 和 torchvision pip install torch1.8.0cu111 torchvision0.9.0cu111 torchaudio0.8.0 -f https://…...

Python基础知识学习与回顾
Python学习 Python基本语法 标识符 标识符由数字、字符串、下划线构成。 注意事项: 标识符不以数字开头区分大小写下划线开头的标识符具有特殊意义保留字,Python保留了一些关键字,这些关键字都是通过小写字母进行保存。 下划线开头的特…...
SpringBoot笔记——(狂神说)——待续
路线 javase: OOPmysql:持久化 htmlcssjsjquery框架:视图,框架不熟练,css不好; javaweb:独立开发MVC三层架构的网站了∶原始 ssm :框架:简化了我们的开发流程,配置也开始较为复杂; war: tomcat运行 spring再简化: SpringBoot - jar:内嵌tomca…...

Linux TCP编程流程
一、TCP编程流程 TCP 提供的是面向连接的、可靠的、字节流服务。TCP的服务器端和客户端编程流程如下: 1.socket()方法 用来创建一个套接字,有了套接字就可以通过网络进行数据的收发。这也是为什么进行网络通信的程序首先要创建一个套接字。创建套接字时…...
pyqt5 QuickStart
在使用pyqt5之前,建议下载一个Anaconda环境,这样下载python包更方便,本篇文章是建立在已经安装好Anaconda的情况下使用的。IDE就是标准的PyCharm了。 一、pyqt包的安装 python终端执行下面两个安装命令: pip install PyQt5 pip …...

Qt6 for Windows 环境搭建(Visual Studio)
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 在 Windows 中,如果想要开发 Qt 应用程序,可以选择多种方式: Qt Creator MinGW 编译器Qt Creator MSVC 编译器Visual Studio࿰…...

探索未知世界:桌面端3D GIS引领地理信息新时代
近年来,桌面端的三维地理信息系统(3D GIS)在地理信息领域迎来了显著的发展,为我们带来了更深入、更丰富的地理空间认知和数据分析体验。从城市规划到环境保护,从资源管理到应急响应,桌面端的3D GIS正逐渐成…...
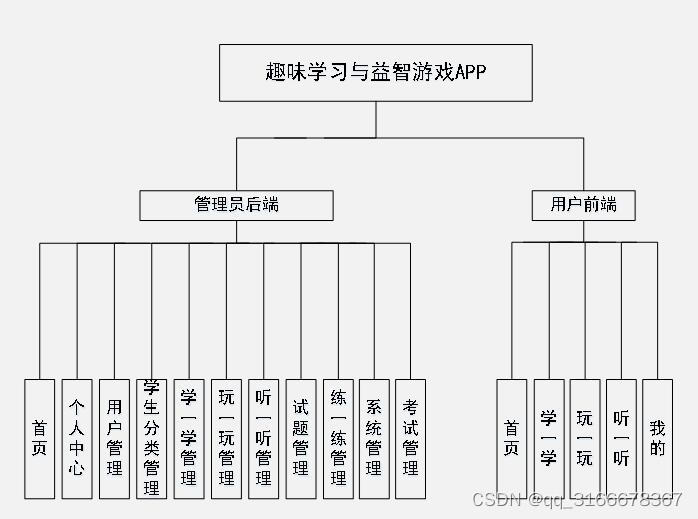
微信小程序 趣味学习与益智游戏系统APP
管理员、用户可通过HBuilder系统手机打开系统,注册登录后可进行管理员后端;首页、个人中心、用户管理、学生分类管理、学一学管理、玩一玩管理、听一听管理、试题管理、练一练管理、系统管理、考试管理,用户前端;首页、学一学、玩…...
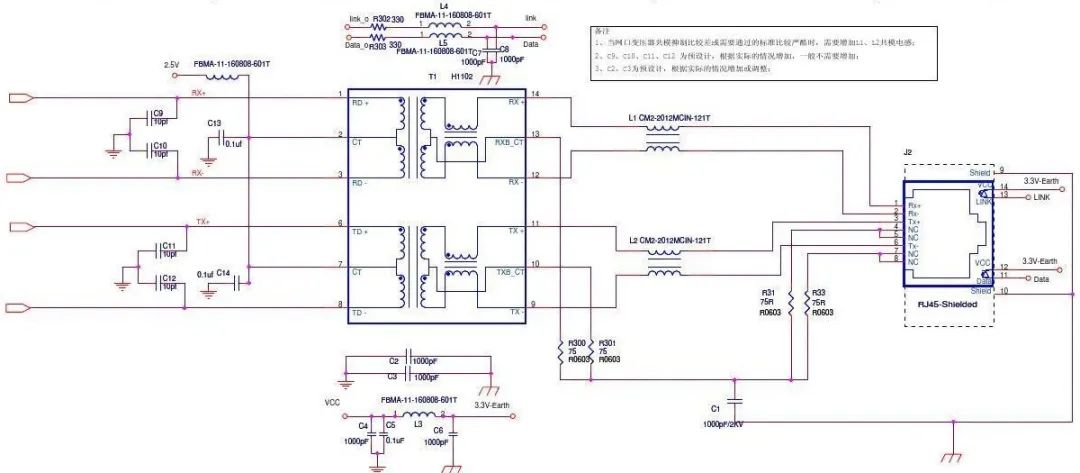
【单片机】UART、I2C、SPI、TTL、RS232、RS422、RS485、CAN、USB、SD卡、1-WIRE、Ethernet等常见通信方式
在单片机开发中,UART、I2C、RS485等普遍在用,这里做一个简单的介绍 UART通用异步收发器 UART口指的是一种物理接口形式(硬件)。 UART是异步(指不使用时钟同步,依靠帧长进行判断),全双工(收发…...
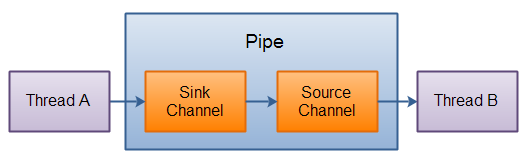
【Java从0到1学习】13 Java IO流
1. 流 1.1 流的概念 流(stream)的概念源于UNIX中管道(pipe)的概念。在UNIX中,管道是一条不间断的字节流,用来实现程序或进程间的通信,或读写外围设备、外部文件等。 一个流,必有源端和目的端,它们可以是计算机内存的…...

linux并发服务器 —— 多进程并发(四)
进程概述 程序是包含一系列信息的文件,描述了如何在运行时创建一个进程; 进程是正在运行的程序的实例,可以用一个程序来创建多个进程; 用户内存空间包含程序代码以及代码所使用的变量,内核数据结构用于维护进程状态…...
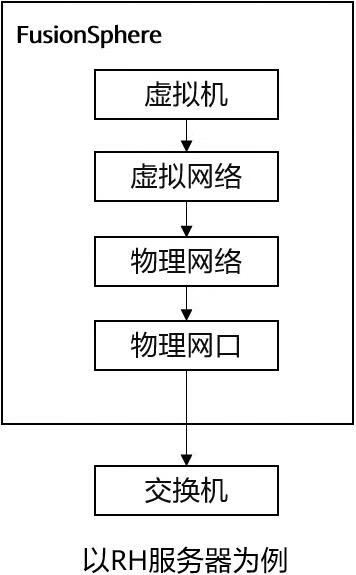
华为云Stack的学习(四)
五、Service OM资源管理 1.Service OM简介 1.1 Service OM介绍 在华为云Stack解决方案中,Service OM是FusionSphere OpenStack的操作管理界面,是资源池(计算、存储、网络)以及基础云服务的管理工具。 1.2 Service OM定位 Serv…...

Midjourney 完整版教程(从账号注册到设计应用)
目录 一、Midjourney 介绍 二、Midjourney 的AI出图示例 三、手把手教你上手Midjourney 1、账号&初始化 1.1 账号注册登录 1.2 账号付费 1.3 账号初始化 2、Midjourney的基础设置 3、Midjourney 出图步骤。 (一)直接描述出图 (二)垫图生图。 4、Midjourney的…...

保护香港服务器的方法
保护香港服务器的方法 当你把一个香港服务器完全留给一个组织、应用程序或个人使用时,它被称为香港服务器租用。在这种类型的主机配置中,客户端将会借出整个服务器,并且不允许其他任何人使用它。 如果您计划使用香港服务器,安全性…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
