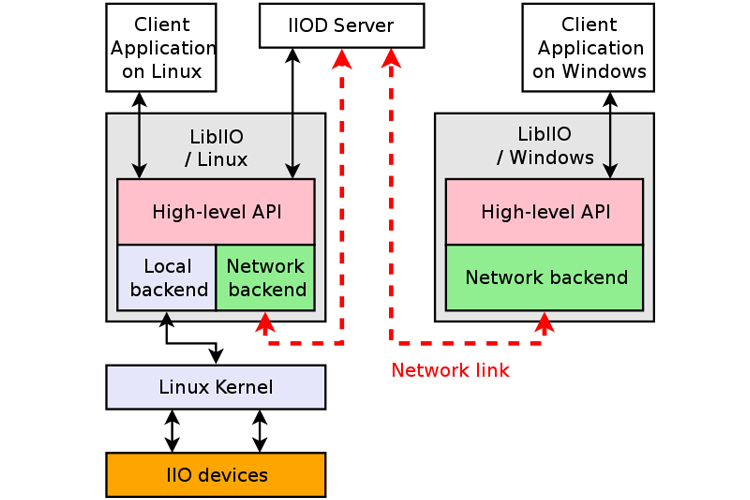
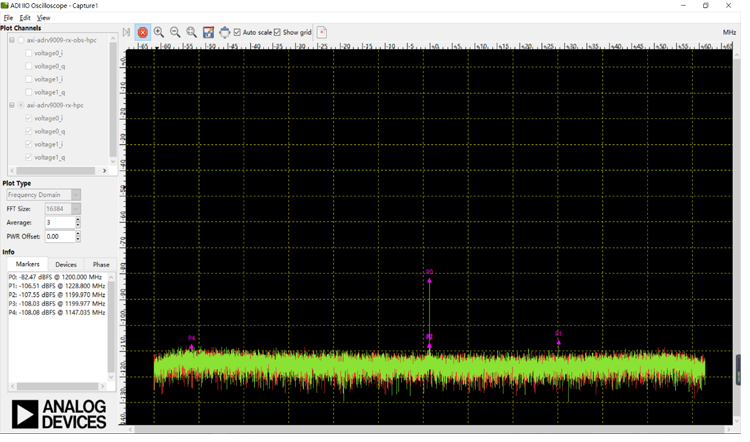
ADRV9009子卡 设计原理图:FMCJ450-基于ADRV9009的双收双发射频FMC子卡 便携测试设备
| FMCJ450-基于ADRV9009的双收双发射频FMC子卡 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
相关文章:
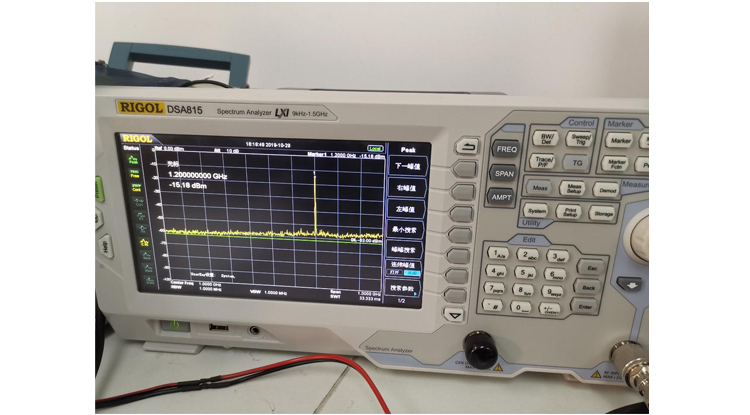
ADRV9009子卡 设计原理图:FMCJ450-基于ADRV9009的双收双发射频FMC子卡 便携测试设备
FMCJ450-基于ADRV9009的双收双发射频FMC子卡 一、板卡概述 ADRV9009是一款高集成度射频(RF)、捷变收发器,提供双通道发射器和接收器、集成式频率合成器以及数字信号处理功能。北京太速科技,这款IC具备多样化的高性能和低功耗组合,FMC子…...

Linux 桌面上的 Firefox 面临着大问题
导读毫无疑问,无论是在桌面、笔记本电脑还是移动设备上,浏览器都是任何操作系统中最重要的应用之一。 如果没有一个功能强大、快速且稳定的浏览器,操作系统的实用性将大幅度降低,以至于我相当确定,如果一个操作系统没有…...

查漏补缺 - 构造函数,原型,this,原型链,继承
目录 1,构造函数2,原型3,this4,原型链1,特点2,Object.prototype.toString()3,instanceof 运算符4,Object.getPrototypeOf()5,创建空原型对象6,面试题 5&#…...
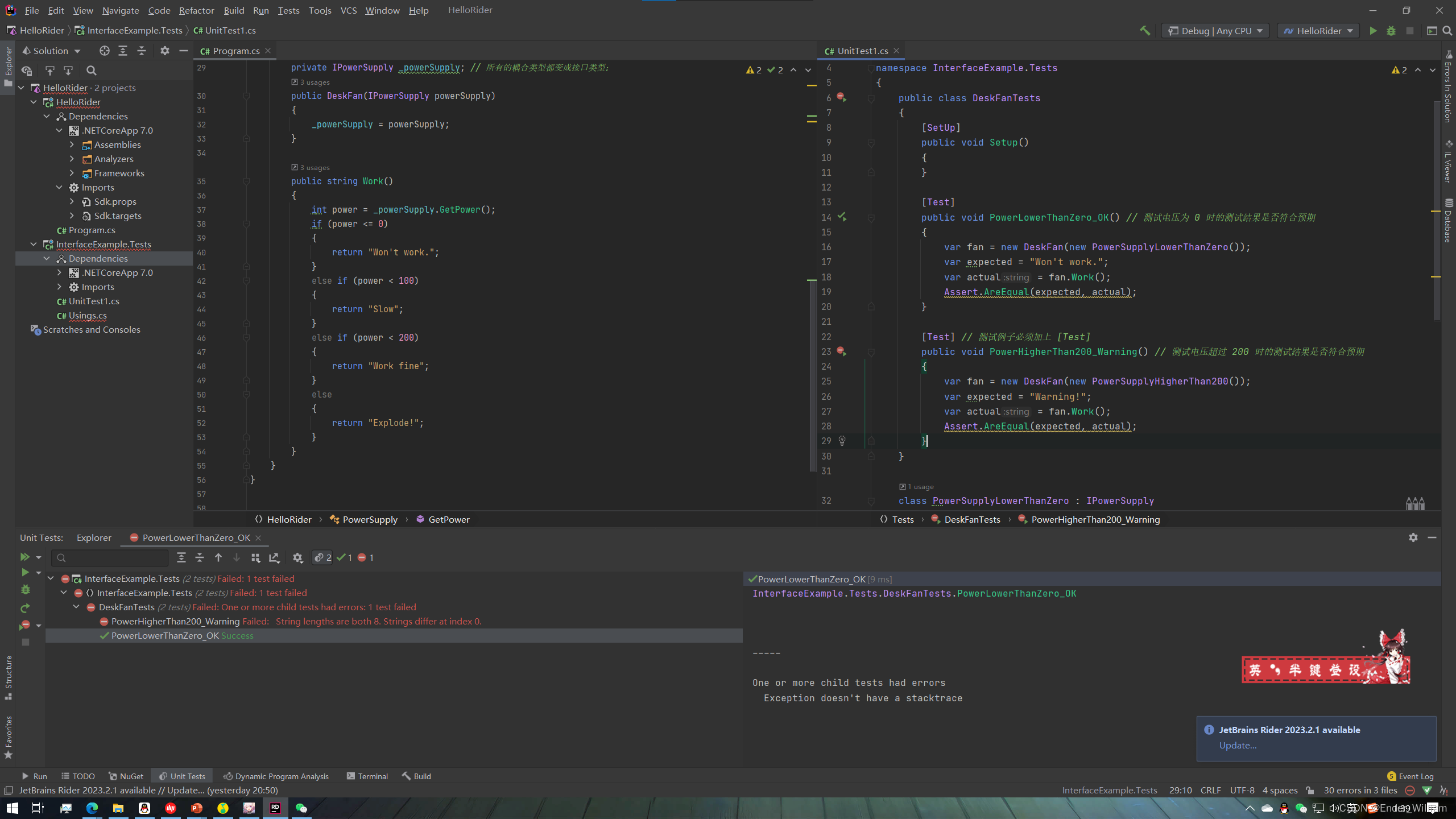
C# 学习笔记--个人学习使用 <2>
C# 学习笔记 Chapter 2 比较硬的基础部分Section 1 委托Part 1 Action 与 func 委托的示例Part 2 自定义委托Part 3 委托的一般使用Part 4 委托的高级使用Part 5 适时地使用接口 Interface 取代一些对委托的使用 Section 2 事件Part 1 初步了解事件Part 2 事件的应用Part 3 事件…...

Linux网络编程Socket通信6-Libevent移植与使用
目录 libeventlibevent交叉编译并移植libevent安装安装步骤测试代码libevent执行报错解决 libevent_base根节点event_base_newevent_base_freeevent_reinit event_loop循环等待事件event_base_loopevent_base_dispatchevent_base_loopexitevent_base_loopbreak event事件event_…...

c#:委托 泛型委托的使用 泛型约束
委托 在 C# 中,delegate 是一种引用类型,它允许您定义和使用可以引用特定方法的对象。delegate 可以看作是一种函数指针,它可以在运行时动态地调用不同的方法。 以下是一个简单的例子来说明 delegate 的实际作用: // 1. 定义一…...

大数据之linux入门
一、linux是什么 linux操作系统 开发者是林纳斯-托瓦兹,出于个人爱好编写。linux是一个基于posix和unix的多用户、多任务、支持多线程和多CPU的操作系统。 Unix是20世纪70年代初出现的一个操作系统,除了作为网络操作系统之外,还可以作为单…...
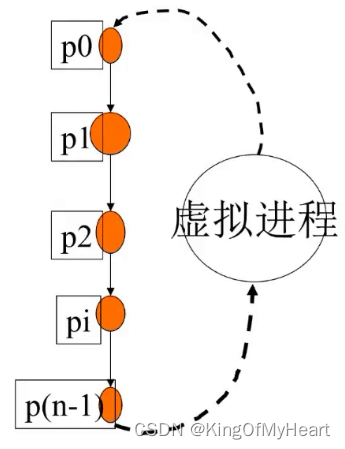
MPI之MPI_Sendrecv接口以及空进程概念介绍
MPI_Sendrecv函数原型 int MPI_Sendrecv(const void *sendbuf, int sendcount, MPI_Datatype sendtype, int dest, int sendtag,void *recvbuf, int recvcount, MPI_Datatype recvtype, int source, int recvtag, MPI_Comm comm, MPI_Status *status);其中各个参数的含义如下&…...

Revit SDK:PointCurveCreation 创建点来拟合曲线
前言 这个例子通过留个例子来展示如何通过点来拟合曲线或者曲面。 内容 PointsParabola 生成抛物线的核心逻辑: double yctr 0; XYZ xyz null; ReferencePoint rp null; double power 1.2; while (power < 1.5){double xctr 0;double zctr 0;while (…...
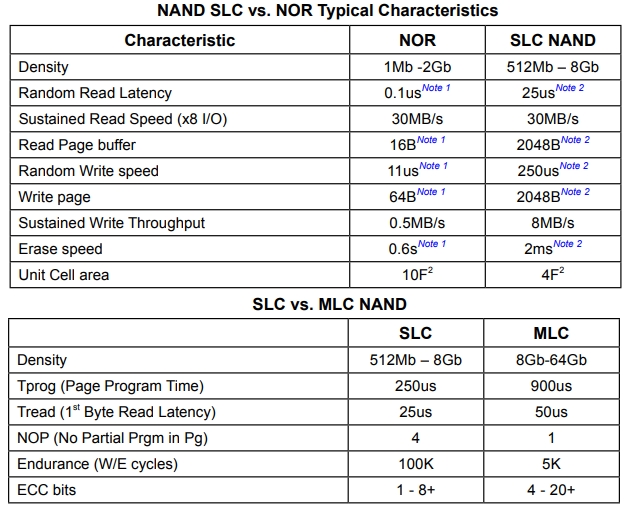
嵌入式Linux开发实操(十五):nand flash接口开发
# 前言 flash memory,分NAND和NOR: 如果说nor flash有个特点就是能执行代码,NOR并行接口具有地址和数据总线,spi flash更是主要用于存储代码,SPI(或QSPI)NOR代码可就地执行(XiP),一般系统要求flash闪存提供相对较高的频率和数据缓存的clocking。而nand flash主要用于…...
vue2 组件库之vetur提示
当我们开发完自定义UI组件库后,在项目中使用时,想要达到以下提示效果,组件提示与属性提示,有什么解决方案呢: 事实上,这是vetur的功能,原文如下: Component Data | Vetur If a pac…...
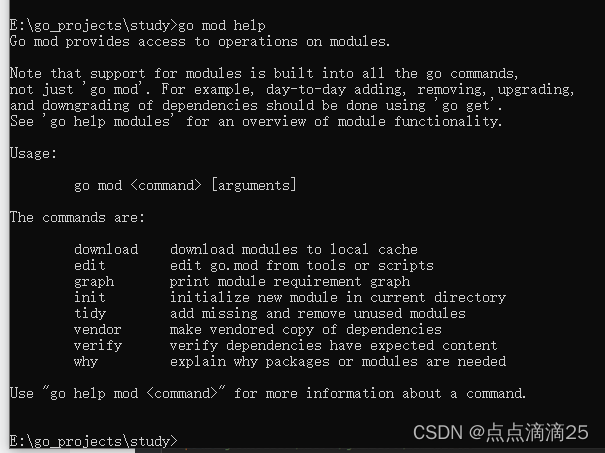
慕课网 Go工程师 第三周 package和gomodules章节
Go包的引入: 包名前面加匿名,只引入但不使用,如果对应包有init函数,会执行init函数(初始化操作) 包名前面加. 把这个包的结构体和方法导入当前包,慎用,你不知道当前包和被引入的包用…...

【ES6】JavaScript 中的数组方法reduce
reduce() 是一个 JavaScript 中的数组方法,它会对数组的每个元素执行一个提供的 reducer 函数,将其减少到一个单一的值。 这是 reduce() 的基本用法: //(method) Array<number>.reduce(callbackfn: (previousValue: number, currentV…...
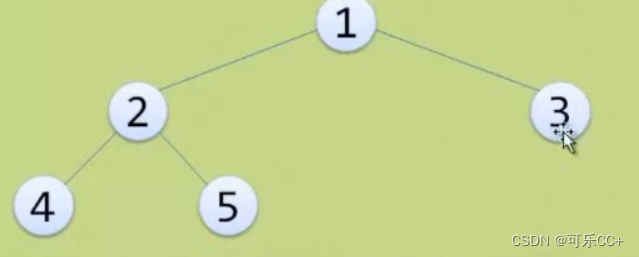
数据结构--树4.2(二叉树)
目录 一、二叉树的定义和特点 1、定义 2、特点 二、二叉树的基本形态 1、空二叉树 2、只有一个根结点 3、根结点只有左子树 4、根结点只有右子树 5、根结点既有左子树又有右子树 6、斜树 7、满二叉树 8、满二叉树和完全二叉树 三、二叉树的性质 一、二叉树的定义和…...
)
详解Numpy(基于jupyter notbook)
详解Numpy(基于jupyter notbook) 1.创建数组2.数据类型3.数组切片和索引4.Numpy的广播与数组操作5.数组合并与通用函数6.其他通用函数 1.创建数组 #引入numpy包,以后np就代表numpy import numpy as npanp.arange(10,30,2)#10为起点ÿ…...
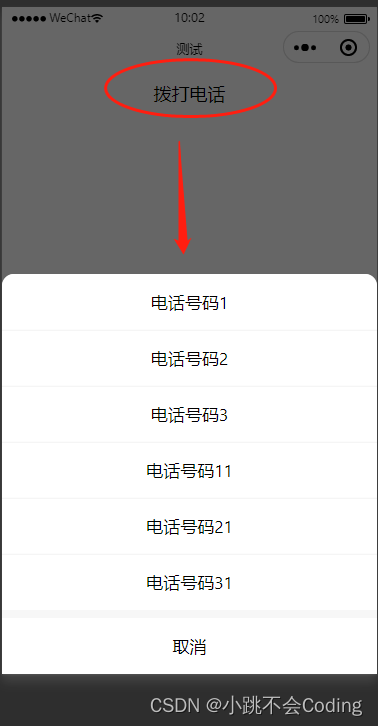
uniapp实现:点击拨打电话,弹出电话号码列表,可以选择其中一个进行拨打
一、实现效果: 二、代码实现: 在uni-app中,使用uni.showActionSheet方法实现点击拨打电话的功能,并弹出相关的电话列表供用户选择。 当用户选择了其中一个电话后,会触发success回调函数,并通过res.tapInde…...

swc-loader Segmentation fault “$NODE_EXE“ “$NPM_CLI_JS“ “$@“
webpack swc swc还不是很稳定。 在swcrc 中有配置plugins 时,swc 转换 /node_modules/ 会报错。 环境 swc/cor1.3.62swc-loader0.2.3swc-plugin-vue-jsx0.2.5 解决 配两套rule,一套处理项目代码,一套处理node_modules webpack.config.js rules:…...
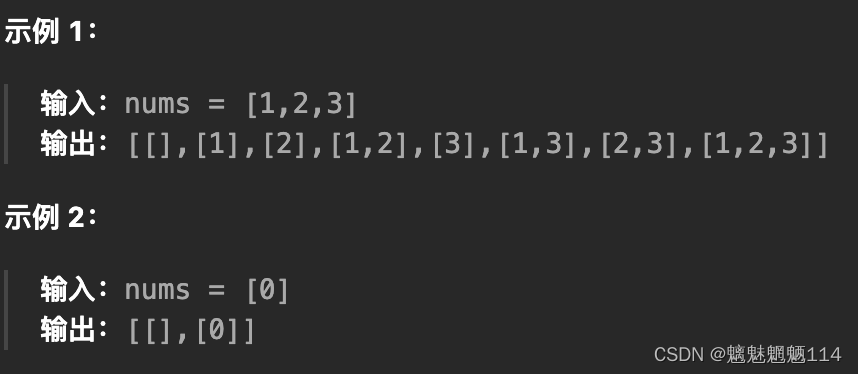
Leetcode78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 回溯法 class Solution {public List<List<Integer>> subsets(int[] nums) {List…...

百度“AI智障”到AI智能体验之旅
目录 前言一、百度PLATO1.抬杠第一名2.听Ta瞎扯淡3.TA当场去世了4.智障与网友的高光时刻 二、文心一言1.设计测试用例2.随意发问3.手机端约会神器 三、体验总结:四、千帆大模型 前言 最近收到了文心一言3.5大模型的内测资格,正巧之前也体验过它的前身&q…...

R中当并行运算遇到C++函数时,让foreach+Rcpp一起工作
目录 方案一:C函数在R包中 方案二:C函数在本地,通过Rcpp::sourceCpp("fun_name.cpp")使用 方案三:将C函数写在当前脚本中 题外话:为什么要研究foreachRcpp? 本文参考: 问题:在fo…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...