【数据结构】二叉数的存储与基本操作的实现
文章目录
- 🍀二叉树的存储
- 🌳二叉树的基本操作
- 🐱👤二叉树的创建
- 🐱👓二叉树的遍历
- 🎡前中后序遍历
- 📌前序遍历
- 📌中序遍历
- 📌后续遍历
- 🛫层序遍历
- 🐱👤前中后序代码实现(递归)
- 🚩前序遍历
- 🚩中序遍历
- 🚩后续遍历
- 🛬前中后序练习题
- 🐱🏍二叉树的基本操作
- 🎈获取树中节点的个数
- 🎈获取叶子节点的个数
- 🎈获取第K层节点的个数
- 🎈 获取二叉树的高度
- 🎈检测值为value的元素是否存在
- ⭕总结

🍀二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储
这里博主讲一下链式存储
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式
二叉表示:
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
三叉表示:
/
/ 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}
这里博主主要讲解一下孩子表示法
🌳二叉树的基本操作
🐱👤二叉树的创建
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树。
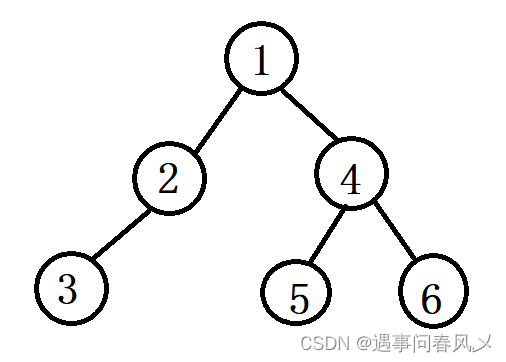
创建如下:
public class BinaryTree{public static class BTNode{BTNode left;BTNode right;int value;BTNode(int value){this.value = value;}}private BTNode root;public void createBinaryTree(){BTNode node1 = new BTNode(1);BTNode node2 = new BTNode(2);BTNode node3 = new BTNode(3);BTNode node4 = new BTNode(4);BTNode node5 = new BTNode(5);BTNode node6 = new BTNode(6);root = node1;node1.left = node2;node2.left = node3;node1.right = node4;node4.left = node5;node5.right = node6;}
}
注意:上述代码并不是创建二叉树的方式,真正创建二叉树方式后序详解重点讲解
在我们对二叉树进行基本操作之前,我们的先来回顾以下二叉树
二叉树是:
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成的
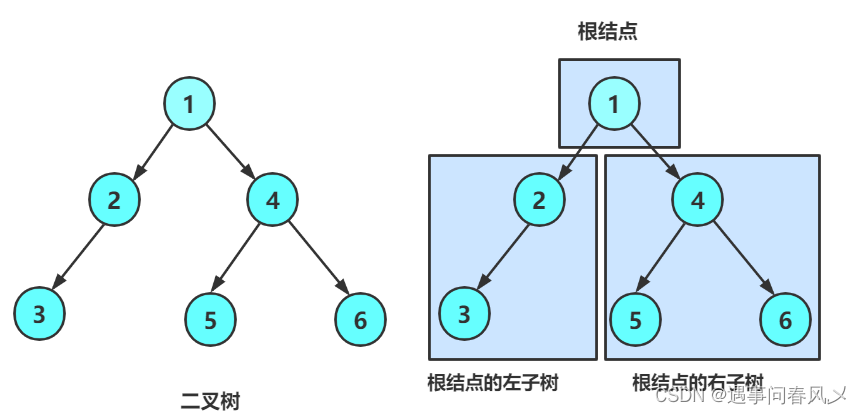
从概念中可以看出,二叉树的每一个子树又是一个新的二叉树,所以可以知道二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
🐱👓二叉树的遍历
🎡前中后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1) 。
遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点,L代表根节点的
左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
-
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。
-
LNR:中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。
-
LRN:后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点
📌前序遍历
前序遍历(Preorder Traversal 亦称先序遍历)规则为
访问根结点—>根的左子树—>根的右子树
比如以下二叉树:
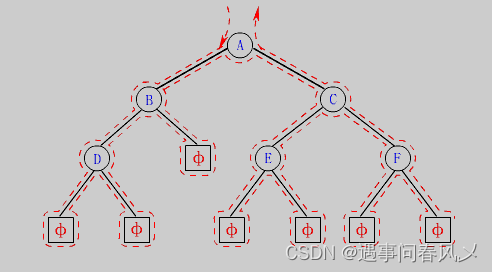
前序遍历的顺序为:
1.== 遍历A结点==
2. 遍历A结点的左子树
3. 遍历B结点
4. 遍历B结点的左子树
5. 遍历D结点
6. 判断D的左右子树为空后返回
7. 遍历B结点的右子树,为空返回
8. 此时A结点左子树遍历完,开始遍历A结点右子树
9. 遍历C结点
10.遍历C结点的左子树
11.遍历E结点
12.判断E结点的左右子树为空后返回
13.遍历C结点的右子树
14.遍历F结点
15.判断F结点的左右子树为空后返回
16.自此遍历完毕全部返回
最后前序的遍历结果为:
A->B->D->C->E->F
📌中序遍历
中序遍历(Inorder Traversal)的访问规则为:
根的左子树—>根节点—>根的右子树。
比如以下二叉树:

中序遍历的顺序为:
- 遍历A结点的左子树
- 遍历B结点的左子树
- 遍历D结点的左子树,发现为空返回
- 遍历D结点
- 遍历D结点的右子树,发现为空返回
- 遍历B结点
- 遍历B结点的右子树。发现为空返回
- 此时左子树遍历完成
- 遍历A结点
- 遍历A结点右子树
- 遍历C结点左子树
- 遍历E结点的左子树,发现为空返回
- 遍历E结点
- 遍历E结点的右子树,发现为空返回
- 遍历C结点
- 遍历C结点的左子树
- 遍历F结点的左子树,发现为空返回
- 遍历F结点
- 遍历F结点的右子树,发现为空返回
- 自此遍历完毕全部返回
最后中序的遍历结果为:
D->B->A->E->C->F
📌后续遍历
后序遍历(Postorder Traversal)的访问规则为:
根的左子树—>根的右子树—>根节点
比如以下二叉树:

后续遍历的顺序为:
- 遍历A结点的左子树
- 遍历B结点的左子树
- 遍历D结点的左子树,为空后返回
- 遍历D结点的右子树,为空后返回
- 遍历D结点
- 遍历B结点的右子树,为空后返回
- 遍历B结点
- 遍历A结点的右子树
- 遍历C结点的左子树
- 遍历E结点的左子树,为空后返回
- 遍历E结点的右子树,为空后返回
- 遍历E结点
- 遍历C结点的右子树
- 遍历F结点的左子树,为空后返回
- 遍历F结点的右子树,为空后返回
- 遍历F结点
- 遍历C结点
- 遍历A结点
- 至此遍历完毕,全部返回
最后后序的遍历结果为:
D->B->E->F->C->A
🛫层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。
设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
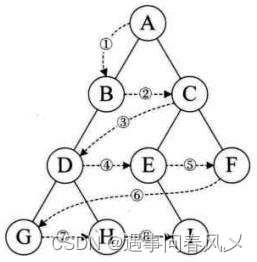
🐱👤前中后序代码实现(递归)
我们发现二叉树本质上是一个个小二叉树组成的
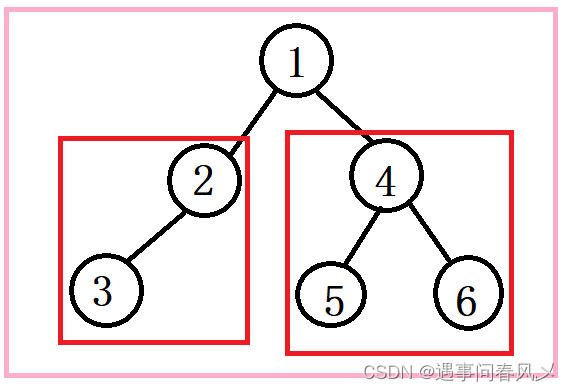
那我们递归不就是把大事化小,复杂变简单吗?
因此我们就可以利用递归的思想进行实现
我们二叉树看成最简单的,也就下面几种情况
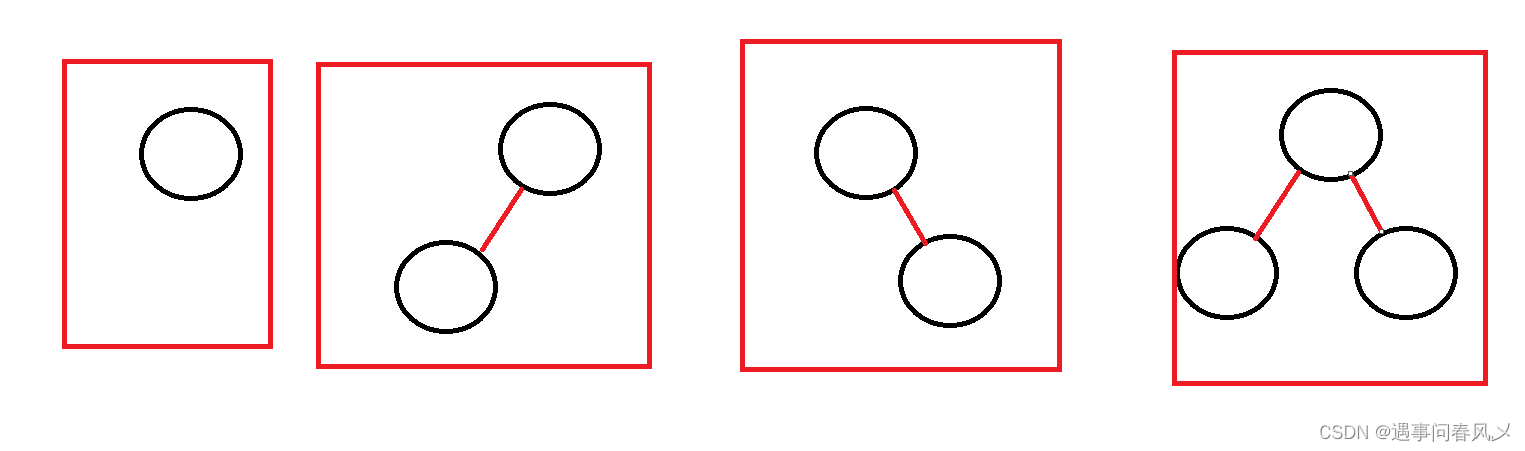
我们从根节点开始遍历,遇到空然后返回打印当前结点就好
🚩前序遍历
// 前序遍历 根 左子树 右子树 递归public void preOrder(TreeNode root) {if(root == null) {return;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}
🚩中序遍历
// 中序遍历public void inOrder(TreeNode root) {if(root == null) {return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}
🚩后续遍历
// 后序遍历public void postOrder(TreeNode root) {if(root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}
🛬前中后序练习题
-
某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为(A)
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA -
二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为(A)
A: E B: F C: G D: H -
设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为(D)
A: adbce B: decab C: debac D: abcde -
某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为(A)
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
总结:给出前序遍历与中序遍历和给出后序遍历与中序遍历可以确定一个二叉树,但是不给中序遍历或者只给一个中序遍历,是无法确定一个二叉树的
🐱🏍二叉树的基本操作
🎈获取树中节点的个数
依旧利用递归的思想,遍历每一棵小树,若当前结点为空,返回0
先获取左节点个数,再获取右节点个数
然后返回两者相加再加上根节点的个数1
比如以下结点:
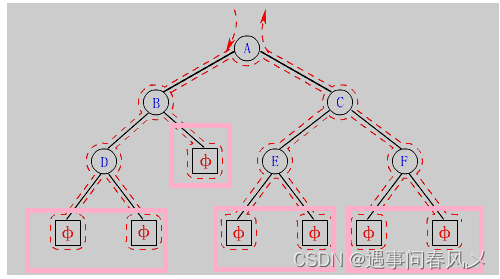
若当前结点不为空,则返回1;
代码实现如下:
public int size(BTNode root) {if (root == null) {return 0;}int leftSize = size(root.left);int rightSize = size(root.right);return leftSize + rightSize + 1;}
🎈获取叶子节点的个数
依旧利用递归的思想,遍历每一棵小树,若当前结点为空,返回0
当前节点的左右子树若都为空,说明该节点为叶子结点,返回1
先获取左节点个数,再获取右节点个数
然后两者相加
代码实现如下:
int getLeafNodeCount(BTNode root) {if(root == null) {return 0;}if(root.left == null && root.right == null){return 1;}int leftSize = getLeafNodeCount(root.left);int rightSize = getLeafNodeCount(root.right);return leftSize+rightSize;}
🎈获取第K层节点的个数
依旧利用递归的思想,每进去一次,K-1,当k=1时,此时若该节点不为空则返回1
为空则返回0
先遍历左子树k层结点,再遍历右子树k层结点
最后左子树结点加上右子树结点,就是该层结点总数
int getKLevelNodeCount(TreeNode root,int k) {if(root == null) {return 0;}if(k == 1) {return 1;}int leftSize = getKLevelNodeCount(root.left,k-1);int rightSize = getKLevelNodeCount(root.right,k-1);return leftSize+rightSize;}
🎈 获取二叉树的高度
分别统计左右子树的高度,然后进行比较
返回高度高的子树并加上根节点
public int maxDepth(BTNode root) {if(root == null) {return 0;}int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);return (leftHeight > rightHeight) ?(leftHeight+1):(rightHeight+1);}
🎈检测值为value的元素是否存在
依旧利用递归的思想
先遍历左子树,若没有找到,则返回null
若返回不为null,则返回该结点
若左子树没有,则遍历右子树,道理相同
若最后都没找到,则返回null;
BTNode find(BTNode root, int val) {if (root == null) {return null;}if (root.val == val) {return root;}BTNode leftTree = find(root.left, val);if (leftTree != null) {return leftTree;}BTNode rightTree = find(root.right, val);if (rightTree != null) {return rightTree;}return null;//没有找到}
⭕总结
关于《【数据结构】二叉数的存储与基本操作的实现》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【数据结构】二叉数的存储与基本操作的实现
文章目录 🍀二叉树的存储🌳二叉树的基本操作🐱👤二叉树的创建🐱👓二叉树的遍历🎡前中后序遍历📌前序遍历📌中序遍历📌后续遍历 🛫层序遍历&am…...

使用 Netty 实现群聊功能的步骤和注意事项
文章目录 前言声明功能说明实现步骤WebSocket 服务启动Channel 初始化HTTP 请求处理HTTP 页面内容WebSocket 请求处理 效果展示总结 前言 通过之前的文章介绍,我们可以深刻认识到Netty在网络编程领域的卓越表现和强大实力。这篇文章将介绍如何利用 Netty 框架开发一…...

一篇文章搞定《WebView的优化及封装》
一篇文章搞定《WebView的优化及封装》 前言WebView的过程分析确定优化方案一、预加载,复用缓冲池(初始化优化)优化的解析说明具体的实现 二、预置模版(请求、渲染优化)优化的解析说明具体的实现1、离线包2、预获取数据…...
FreeSWITCH 1.10.10 简单图形化界面5 - 使用百度TTS
FreeSWITCH 1.10.10 简单图形化界面5 - 使用百度TTS 0、 界面预览1、注册百度AI开放平台,开通语音识别服务2、获取AppID/API Key/Secret Key3、 安装百度语音合成sdk4、合成代码5、在PBX中使用百度TTS6、音乐文件-TTS7、拨号规则-tts_command 0、 界面预览 http://…...
DP读书:不知道干什么就和我一起读书吧
DP读书:不知道干什么就和我一起读书吧 为啥写博客:好处一:记录自己的学习过程优点二:让自己在各大社群里不那么尴尬推荐三:坚持下去,找到一个能支持自己的伙伴 虽然清楚知识需要靠时间沉淀,但在…...
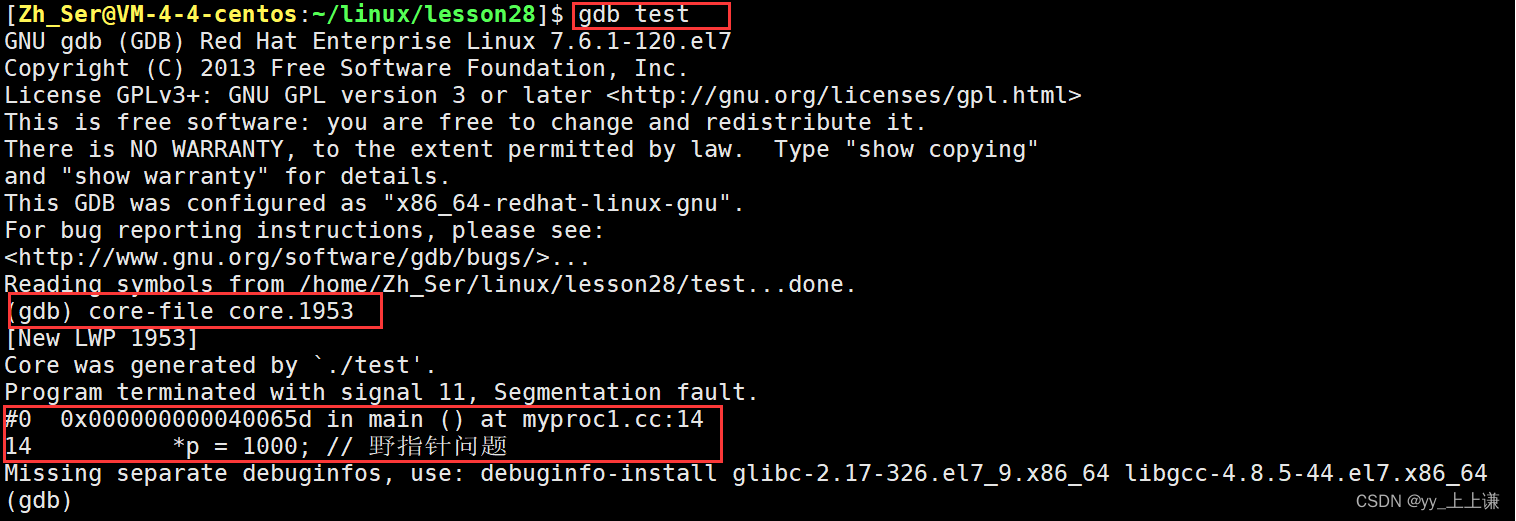
【Linux】进程通信 — 信号(上篇)
文章目录 📖 前言1. 什么是信号1.1 认识信号:1.2 信号的产生:1.3 信号的异步:1.4 信号的处理: 2. 前后台进程3. 系统接口3.1 signal:3.1 - 1 不能被捕捉的信号 3.2 kill:3.2 - 1 killall 3.3 ra…...

JS弃之可惜食之无味的代码冷知识
JS代码冷知识大全 1. 变量提升与暂死 在JavaScript中,变量提升是一个有趣且容易让人误解的概念。在代码中,变量和函数声明会在其所在作用域的顶部被提升,但是初始化并不会被提升。这可能导致在声明之前就使用变量,结果为undefin…...

数据结构初阶--排序
目录 一.排序的基本概念 1.1.什么是排序 1.2.排序算法的评价指标 1.3.排序的分类 二.插入排序 2.1.直接插入排序 2.2.希尔排序 三.选择排序 3.1.直接选择排序 3.2.堆排序 重建堆 建堆 排序 四.交换排序 4.1.冒泡排序 4.2.快速排序 快速排序的递归实现 法一&a…...

赴日IT 如何提高去日本做程序员的几率?
其实想去日本做IT工作只要满足学历、日语、技术三个必要条件,具备这些条件应聘就好,不具备条件你就想办法具备这些条件,在不具备条件之前不要轻易到日本去,日本IT行业虽然要求技术没有国内那么高,但也不是随便好进入的…...

c# 使用了 await、asnync task.run 三者结合使用
在 C# 异步编程中,await 和 async 关键字结合使用可以让你更方便地编写异步代码,而无需直接使用 Task.Run。然而,有时候你可能仍然需要使用 Task.Run 来在后台线程上执行某些工作,这取决于你的代码逻辑和需求。 await 和 async 关…...

C#获取屏幕缩放比例
现在1920x1080以上分辨率的高分屏电脑渐渐普及了。我们会在Windows的显示设置里看到缩放比例的设置。在Windows桌面客户端的开发中,有时会想要精确计算窗口的面积或位置。然而在默认情况下,无论WinForms的Screen.Bounds.Width属性还是WPF中SystemParamet…...

Rn实现省市区三级联动
省市区三级联动选择是个很频繁的需求,但是查看了市面上很多插件不是太老不维护就是不满足需求,就试着实现一个 这个功能无任何依赖插件 功能略简单,但能实现需求 核心代码也尽力控制在了60行左右 pca-code.json树型数据来源 Administrative-d…...

SpringCloud学习笔记(十)_SpringCloud监控
今天我们来学习一下actuator这个组件,它不是SpringCloud之后才有的,而是SpringBoot的一个starter,Spring Boot Actuator。我们使用SpringCloud的时候需要使用这个组件对应用程序进行监控与管理 在SpringBoot2.0版本中,actuator可以…...

测试理论与方法----测试流程的第二个环节:测试计划
二、软件测试分类与测试计划 1、软件测试的分类(理解掌握) 根绝需求规格说明书,在设计阶段会产出的两个文档: 概要设计(HLD):设计软件的结构,包含软件的组成,模块之间的层次关系,模块与模块之间的调用关系…...
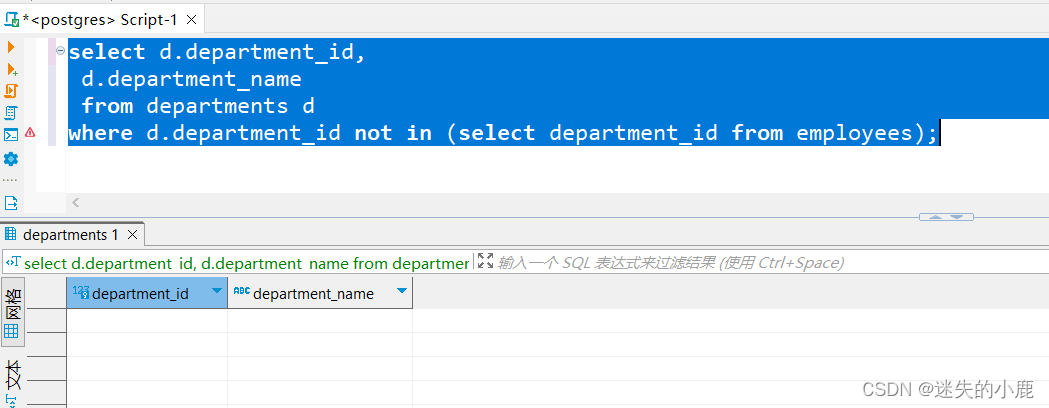
postgresql-子查询
postgresql-子查询 简介派生表IN 操作符ALL 操作符ANY 操作符关联子查询横向子查询EXISTS 操作符 简介 子查询(Subquery)是指嵌套在其他 SELECT、INSERT、UPDATE 以及 DELETE 语句中的 查询语句。 子查询的作用与多表连接查询有点类似,也是为…...

Linux 系统运维工具之 OpenLMI
一、前要 OpenLMI(全称 Open Linux Management Infrastructure)即开放式的 Linux 管理基础架构。OpenLMI 是一个开源项目,用于管理 Linux 系统管理的通用基础架构。它建立在现有工具基础上,充当抽象层,以便向系统管理…...
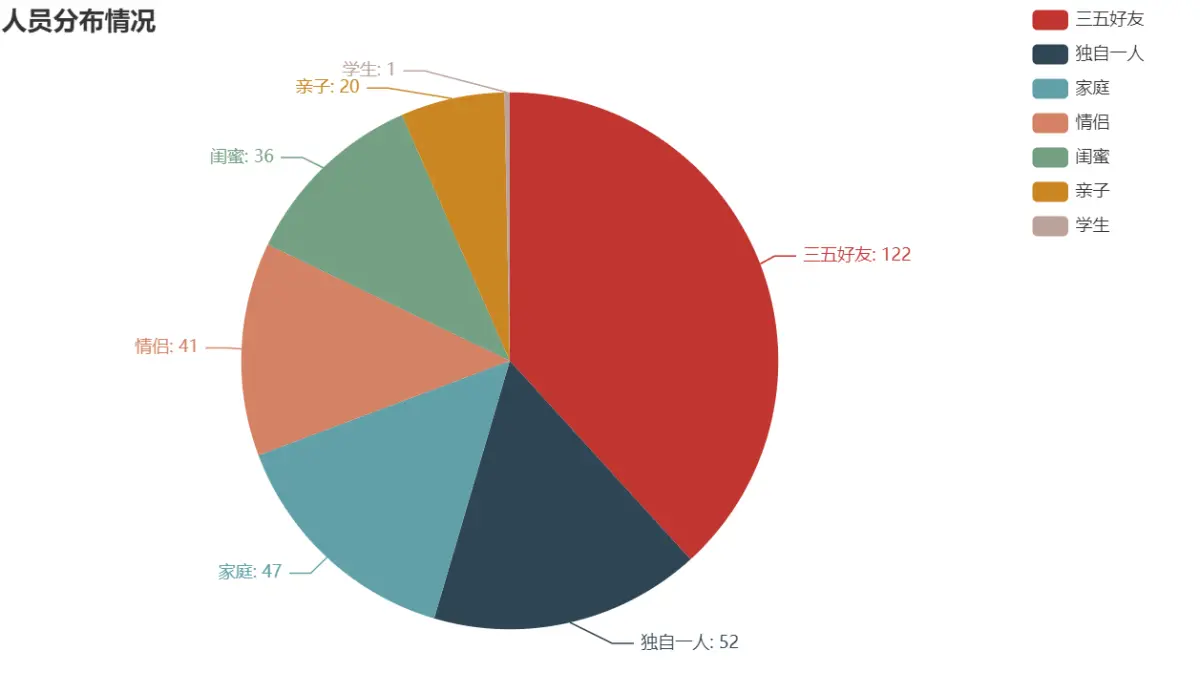
8天长假快来了,Python分析【去哪儿旅游攻略】数据,制作可视化图表
目录 前言环境使用模块使用数据来源分析 代码实现导入模块请求数据解析保存 数据可视化导入模块、数据年份分布情况月份分布情况出行时间情况费用分布情况人员分布情况 前言 2023年的中秋节和国庆节即将来临,好消息是,它们将连休8天!这个长假…...

【HSPCIE仿真】输入网表文件(5)基本仿真输出
仿真输出 1. 概述1.1 输出变量1.2 输出分析类型 2. 显示仿真结果2.1 .print语句基本语法示例 2.2 .probe 语句基本语法示例 2.3 子电路的输出2.4 打印控制选项.option probe.option post.option list.option ingold 2.5 .model_info打印模型参数 3. 仿真输出参数的选择3.1 直流…...
uni-app中使用iconfont彩色图标
uni-app中使用iconfont彩色图标 大家好,今天我们来学习一下uni-app中使用iconfont彩色图标,好好看,好好学,超详细的 第一步 首先,从iconfont官网(iconfont-阿里巴巴矢量图标库)选择自己需要的图…...
Hystrix: Dashboard流监控
接上两张服务熔断 开始搭建Dashboard流监控 pom依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocat…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...
