当前位置： 首页 > news >正文

detour编译问题及导入visual studio

news 2026/2/11 2:50:28

Detours是经过微软认证的一个开源Hook库，Detours在GitHub上，网址为 https://github.com/Microsoft/Detours
注意版本不一样的话也是会出问题的，因为我之前是vs2022的所以之前的detours.lib不能使用，必须用对应版本的x64 Native Tools Command Prompt for VS工具进行编译
我这里使用的visual studio2019版本，那么我需要用vs2019的nmake进行编译

x64 Native Tools Command Prompt for VS 2019

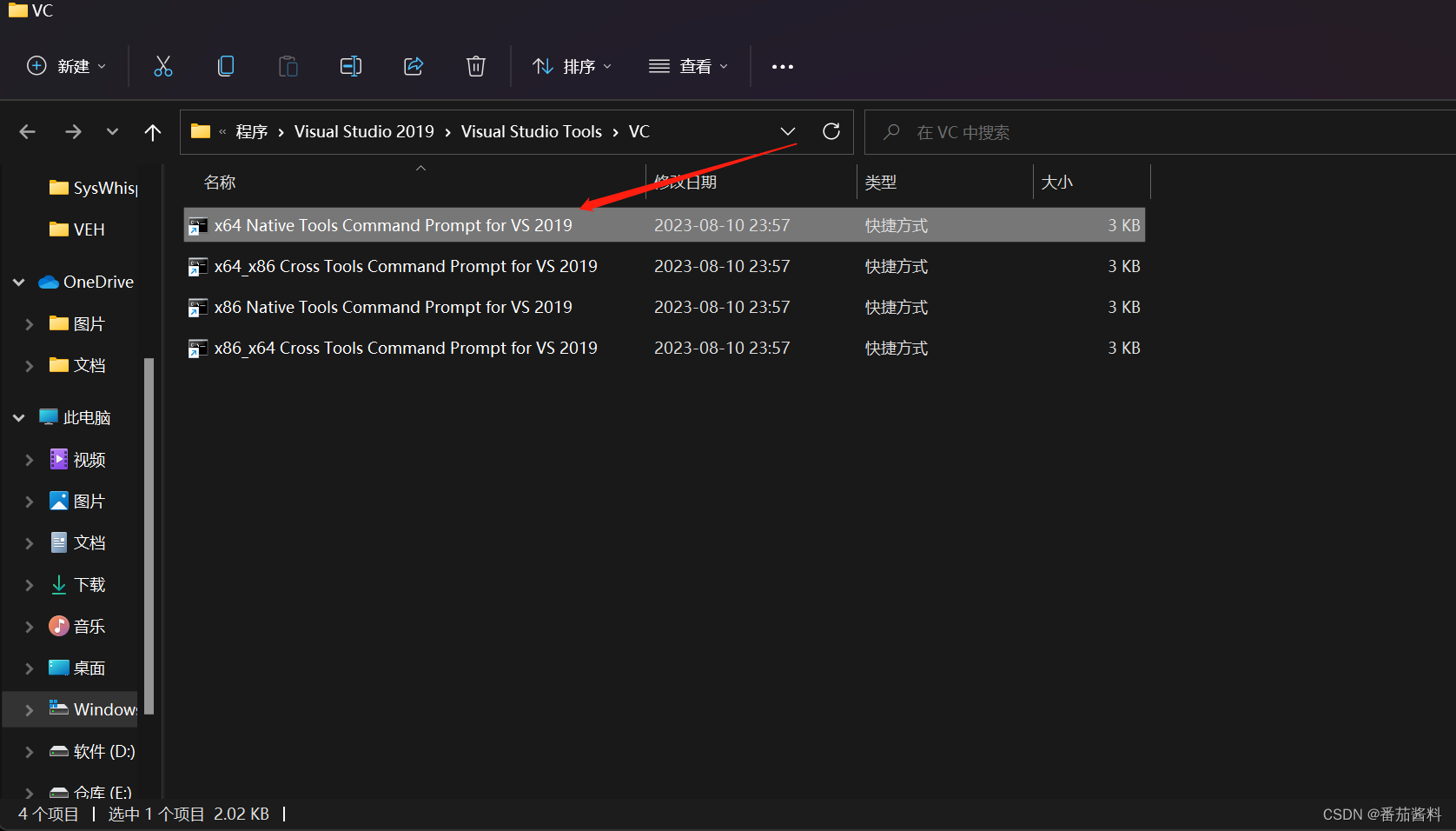
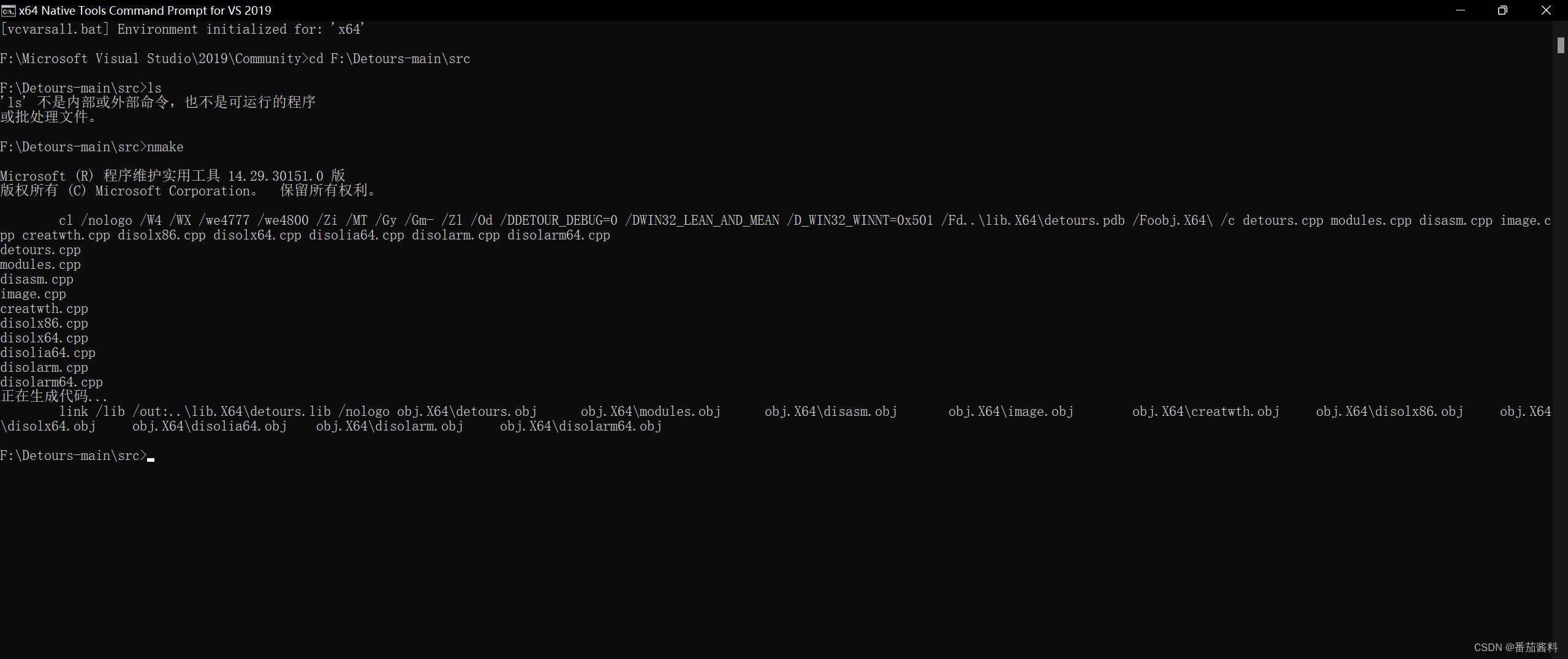
在这里插入图片描述
在这里插入图片描述
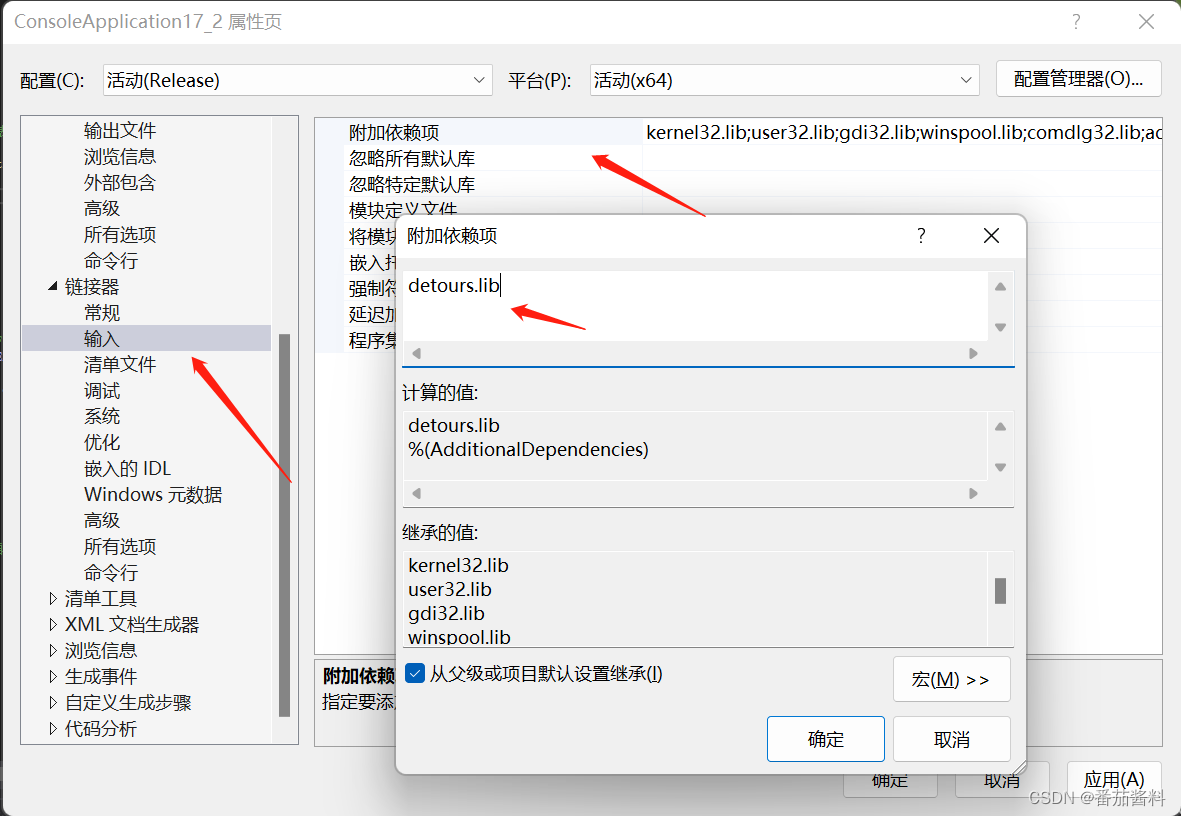
detours导入visual studio
此时我的detours.lib存放在D盘根目录下
完成以下三步骤即可
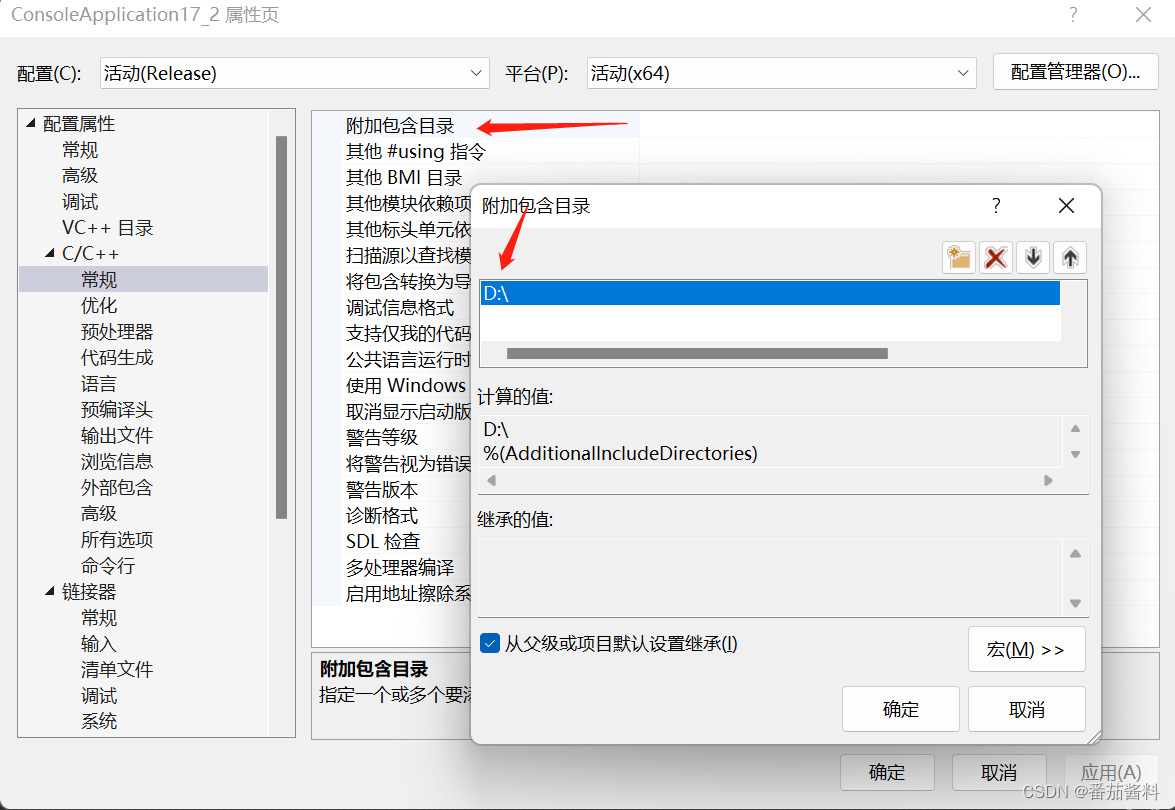
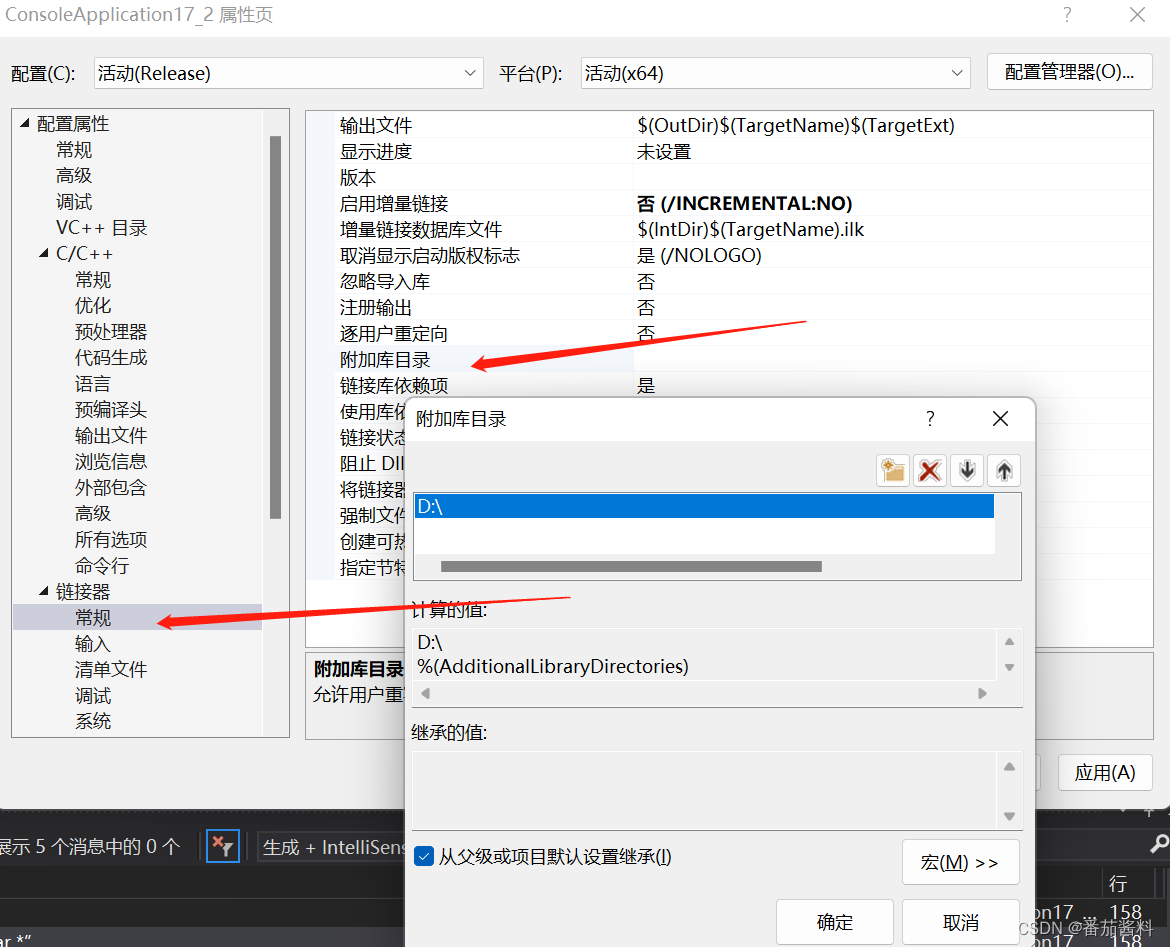
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

相关文章：

detour编译问题及导入visual studio

Detours是经过微软认证的一个开源Hook库，Detours在GitHub上，网址为 https://github.com/Microsoft/Detours 注意版本不一样的话也是会出问题的，因为我之前是vs2022的所以之前的detours.lib不能使用，必须用对应版本的x64 Native To…...

编程日记 2023/8/31 8:08:59

江西武功山旅游攻略(周末两日游)

一、 往返路线 1: 出发路线 周五晚上上海出发坐火车🚄到江西萍乡(11.5小时,卧铺550左右) 打车到江西武功山景区,120-150元左右,人均30元,1小时10分左右到达 或者 🚗到达萍乡北之后 出站后步行200米到长途汽车站，乘旅游巴士直达武功山游…...

编程日记 2023/8/31 8:07:58

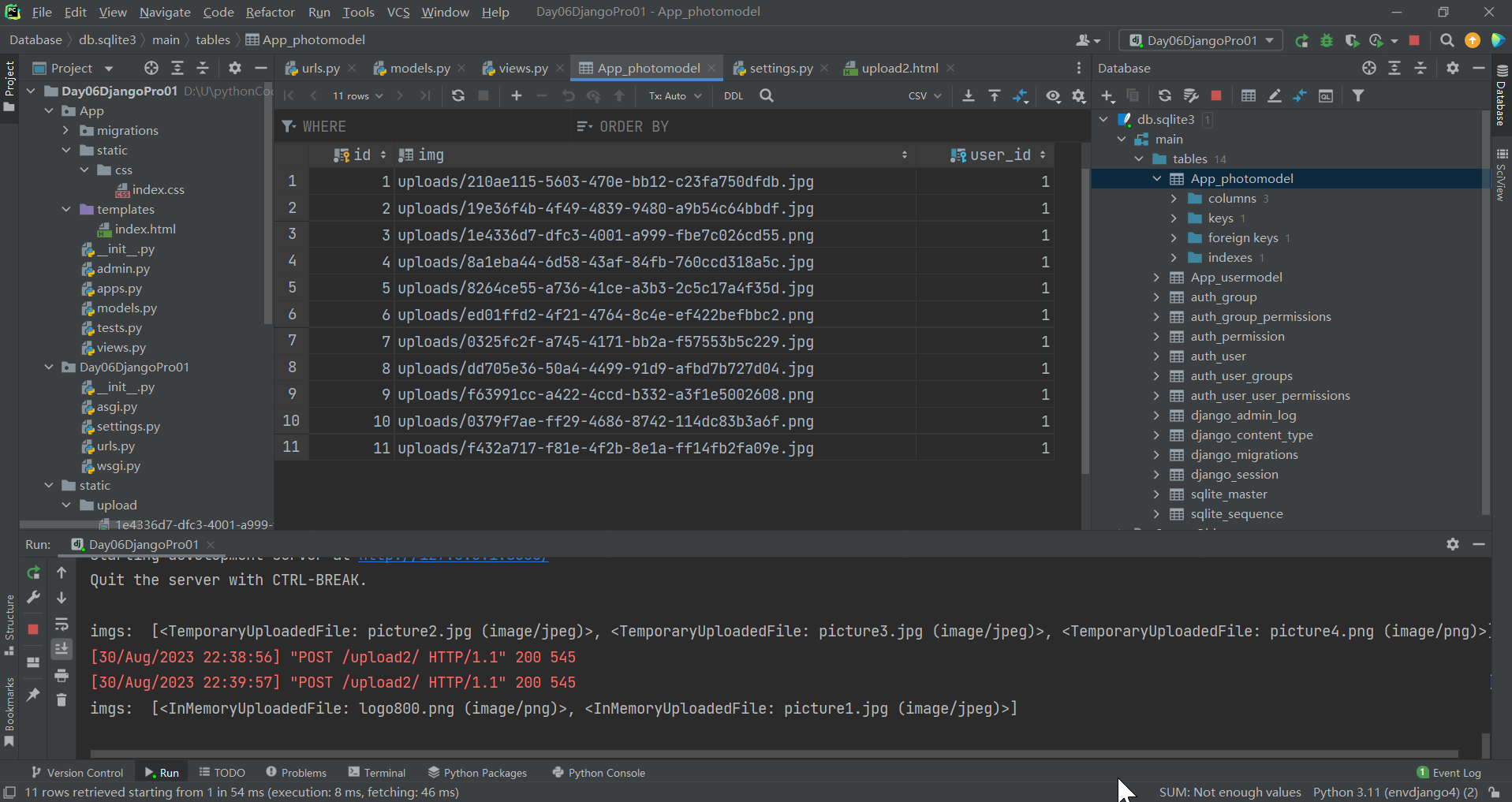
Django静态文件媒体文件文件上传

文章目录 一、静态文件和媒体文件1.在django中使用静态文件实践2.在django中使用媒体文件 二、文件上传单文件上传实践多文件上传 一、静态文件和媒体文件 媒体文件: 用户上传的文件，叫做media 静态文件:存放在服务器的css,js,image,font等 叫做static1.在django中…...

编程日记 2023/8/31 8:06:57

mysql 分库分表实现思路

MySQL的分库分表是一种常用的数据库拆分方案，它可以提高数据库的性能和扩展性。下面是一般的实现步骤： 数据库设计：首先，需要对数据库进行良好的设计。确定要分库分表的实体和关系，并根据业务需求进行合理的拆分。 数…...

编程日记 2023/8/31 8:05:55

Android深思如何防止快速点击

前言 其实快速点击是个很好解决的问题，但是如何优雅的去解决确是一个难题，本文主要是记录一些本人通过解决快速点击的过程中脑海里浮现的一些对这个问题的深思。 作者：流浪汉kylin 链接：https://juejin.cn/post/7197337416096055…...

编程日记 2023/8/31 8:04:54

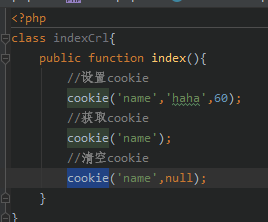
PHP自己的框架cookie()使用（完善篇七）

1、PHP自己的框架cookie() 2、cookie类&#xff08;CookieBase.php&#xff09; <?php class CookieBase {/*** 设置cookie*/public static function set($name, $value, $expire 3600, $path , $domain , $secure false, $httponly false) {setcookie($name, $valu…...

编程日记 2023/8/31 8:03:53

Spring Boot Dubbo Zookeeper（含ZK安装脚本）

文章目录 Spring Boot Dubbo Zookeeper&#xff08;含ZK安装脚本&#xff09;简介DubboCommonProviderConsumer Zookeeper Spring Boot Dubbo Zookeeper&#xff08;含ZK安装脚本&#xff09; 简介 Dubbo Common 公共依赖 <!-- Spring Boot Starter --> <dependen…...

编程日记 2023/8/31 8:02:51

BigDecimal百科全书

一、BigDecimal简述 Java在java.math包中提供的API类BigDecimal&#xff0c;用来对超过16位有效位的数进行精确的运算。双精度浮点型变量double可以处理16位有效数&#xff0c;但在实际应用中&#xff0c;可能需要对更大或者更小的数进行运算和处理。 一般情况下&#xff0c;…...

编程日记 2023/8/31 8:01:50

【30天熟悉Go语言】11 数组的全方位使用与解析

作者&#xff1a;秃秃爱健身&#xff0c;多平台博客专家&#xff0c;某大厂后端开发&#xff0c;个人IP起于源码分析文章 &#x1f60b;。 源码系列专栏&#xff1a;Spring MVC源码系列、Spring Boot源码系列、SpringCloud源码系列&#xff08;含&#xff1a;Ribbon、Feign&…...

编程日记 2023/8/31 8:00:49

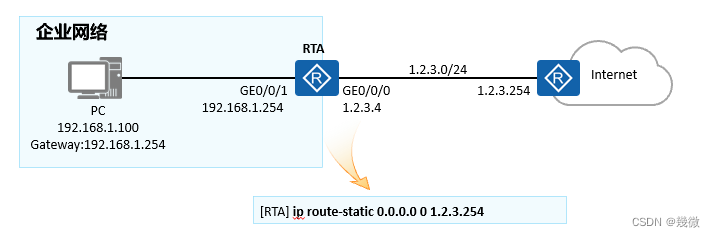
静态路由(详细理解+实例精讲)

系列文章目录 华为数通学习&#xff08;6&#xff09; 前言 一&#xff0c;静态路由 二&#xff0c;静态路由配置 三&#xff0c;缺省路由 四&#xff0c;缺省路由应用场景 总结 前言 随着华为公司的不断发展&#xff0c;数据通信这门技术也越来越重要&#xff0c;很多人…...

编程日记 2023/8/31 7:59:47

leetcode做题笔记118. 杨辉三角

给定一个非负整数 numRows&#xff0c;生成「杨辉三角」的前 numRows 行。 在「杨辉三角」中&#xff0c;每个数是它左上方和右上方的数的和。 思路一&#xff1a;动态规划 int** generate(int numRows, int* returnSize, int** returnColumnSizes){int **returnnum(int **)…...

编程日记 2023/8/31 7:58:46

stm32之24.RTC闹钟usart端口修改配置

&#xff08;需要修改&#xff09; 源码 while(1){//rtc唤醒事件if(g_rtc_wakeup_event){//获取日期RTC_GetDate(RTC_Format_BCD,&RTC_DateStructure);printf("20%02x/%02x/%02xWeek:%x\r\n",RTC_DateStructure.RTC_Year,RTC_DateStructure.RTC_Month,RTC_Date…...

编程日记 2023/8/31 7:57:43

Spring Security无法调用接口错误解决

之前在写程序的时候&#xff0c;发现有个接口使用postmapping发送请求一直无法进行调用 PostMapping("/user/login")public ResponseResult login(User user){//登录&#xff0c;这里登录的时候需要传入用户名和密码System.out.println("user "user.toSt…...

编程日记 2023/8/31 7:56:41

运维Shell脚本小试牛刀(二)

运维Shell脚本小试牛刀(一) 运维Shell脚本小试牛刀(二) 运维Shell脚本小试牛刀(三)::$(cd $(dirname $0)&#xff1b; pwd)命令详解 一: if---else.....fi 条件判断演示 [rootwww shelldic]# cat checkpass.sh #!/bin/bash - # # # # FILE: ch…...

编程日记 2023/8/31 7:55:40

飞天使-python的模块与包与装饰器

文章目录 模块与包标准模块第三方模块自定义模块 高级语法切片迭代器/生成器高级模式&#xff08;闭包&#xff09;高级模式&#xff08;装饰器&#xff09; 参考视频 模块与包 标准模块 import os print(os.getcwd())import sys print(sys.argv) print(sys.platform) print(…...

编程日记 2023/8/31 7:54:39

linux shell脚本利用 kill -0 检查进程是否存在

1.kill -0介绍 kill -0 pid用来检查进程是否存在&#xff0c;kill -0 pid解释(来自man kill)&#xff1a;“If sig is 0, then no signal is sent, but error checking is still performed.”不发送任何信号&#xff0c;但是系统会进行错误检查。 kill -0 pid ->若存在&am…...

编程日记 2023/8/31 7:53:38

抖音视频删了怎么在电脑上找回来

【昨天整理电脑文件时&#xff0c;不小心将剪辑好的抖音作品误删了&#xff0c;但是回收站中找不回来了&#xff0c;这些视频是我花了很多心血制作的&#xff0c;如果没了真的十分可惜&#xff01;希望大家能帮帮我&#xff0c;告诉我应该如何恢复这些文件。】 现在人们都喜欢…...

编程日记 2023/8/31 7:52:37

方面级别情感分析之四元组预测

情感四元组预测现有方法 阅读本文之前我们默认你对情感分析有基本的认识。 如果没有请阅读文章(https://tech.tcl.com/post/646efb5b4ba0e7a6a2da6476) 情感分析四元组预测涉及四个情感元素: 方面术语a&#xff0c;意见术语(也叫观点术语)o&#xff0c; 方面类别ac&#xff0c…...

编程日记 2023/8/31 7:51:36

算法 稀疏数组 数组优化 数组压缩 二维数组转稀疏数组 算法合集（二）

1. 五子棋游戏&#xff0c;玩家对战一半停战休息&#xff0c;此时需要存储当前对战双方棋子信息 a. 采用二维数组存储&#xff1a; 0为空&#xff0c; 1代表黑棋 2代表蓝色棋子 b. 棋盘为11行&#xff0c;11列 > int [][] chessArray new int [11][11]; c. 出现的问题&am…...

编程日记 2023/8/31 7:50:34

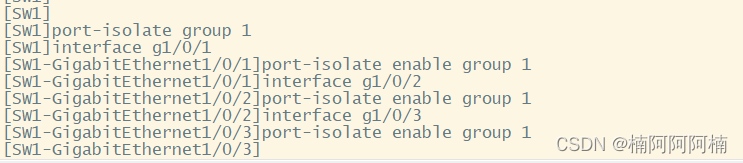
交换机端口安全实验

文章目录 一、实验的背景与目的二、实验拓扑三、实验需求四、实验解法1. PC配置IP地址部分2. 在SW1上开启802.1X身份验证3. 创建一个用户身份验证的用户。用户名为wangdaye&#xff0c;密码为1234564.创建一个端口隔离组&#xff0c;实现三台PC无法互相访问 摘要&#xff1a; 本…...

编程日记 2023/8/31 7:49:32

【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型

摘要 拍照搜题系统采用“三层管道&#xff08;多模态 OCR → 语义检索 → 答案渲染&#xff09;、两级检索&#xff08;倒排 BM25 向量 HNSW&#xff09;并以大语言模型兜底”的整体框架&#xff1a; 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后&#xff0c;分别用…...

编程新知 2026/2/10 23:40:16

51c自动驾驶~合集58

我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留&#xff0c;CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制&#xff08;CCA-Attention&#xff09;&#xff0c;…...

编程新知 2026/2/5 4:25:15

Java 语言特性(面试系列1)

一、面向对象编程 1. 封装&#xff08;Encapsulation&#xff09; 定义&#xff1a;将数据&#xff08;属性&#xff09;和操作数据的方法绑定在一起&#xff0c;通过访问控制符&#xff08;private、protected、public&#xff09;隐藏内部实现细节。示例&#xff1a; public …...

编程新知 2025/10/6 4:03:40

模型参数、模型存储精度、参数与显存

模型参数量衡量单位 M&#xff1a;百万&#xff08;Million&#xff09; B&#xff1a;十亿&#xff08;Billion&#xff09; 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的&#xff0c;但是一个参数所表示多少字节不一定&#xff0c;需要看这个参数以什么…...

编程新知 2025/12/20 12:32:08

（二）TensorRT-LLM | 模型导出（v0.20.0rc3）

0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述&#xff0c;后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作&#xff0c;其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

编程新知 2026/1/24 6:44:11

基于Docker Compose部署Java微服务项目

一. 创建根项目 根项目&#xff08;父项目&#xff09;主要用于依赖管理 一些需要注意的点&#xff1a; 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件&#xff0c;否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

编程新知 2026/2/5 3:09:56

相机Camera日志分析之三十一：高通Camx HAL十种流程基础分析关键字汇总（后续持续更新中）

【关注我，后续持续新增专题博文，谢谢！！！】 上一篇我们讲了：有对最普通的场景进行各个日志注释讲解，但相机场景太多，日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志，通过下列分类关键字搜索，即可清晰的分析不同场景的相机运行流程差异…...

编程新知 2025/11/20 7:13:43

leetcodeSQL解题：3564. 季节性销售分析

leetcodeSQL解题&#xff1a;3564. 季节性销售分析 题目&#xff1a; 表&#xff1a;sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

编程新知 2026/2/10 3:44:54

vue3+vite项目中使用.env文件环境变量方法

vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量&#xff0c;这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

编程新知 2026/1/26 19:12:01

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。

1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj&#xff0c;再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

编程新知 2026/2/5 4:21:48