C/C++每日一练(20230221)

目录
1. 格雷编码
2. 矩阵问题
3. 搜索旋转排序数组 II
1. 格雷编码
格雷编码是一个二进制数字系统,在该系统中,两个连续的数值仅有一个位数的差异。
给定一个代表编码总位数的非负整数 n,打印其格雷编码序列。即使有多个不同答案,你也只需要返回其中一种。
格雷编码序列必须以 0 开头。
示例 1:
输入: 2 输出: [0,1,3,2] 解释:00 - 001 - 111 - 310 - 2对于给定的 n,其格雷编码序列并不唯一。例如,[0,2,3,1] 也是一个有效的格雷编码序列。00 - 010 - 211 - 301 - 1
示例 2:
输入: 0 输出: [0] 解释: 我们定义格雷编码序列必须以 0 开头。给定编码总位数为 n 的格雷编码序列,其长度为 2n。当 n = 0 时,长度为 20 = 1。因此,当 n = 0 时,其格雷编码序列为 [0]。
代码:(原题中的代码,已补充填空部分)
#include <stdio.h>
#include <stdlib.h>int *grayCode(int n, int *returnSize)
{if (n < 0){return NULL;}int i, count = 1 << n;int *codes = (int*)malloc(count * sizeof(int));for (i = 0; i < count; i++){codes[i] = (i >> 1) ^ i;}*returnSize = 1 << n;return codes;
}int main(int argc, char **argv)
{if (argc != 2){fprintf(stderr, "Usage: ./test n\n");exit(-1);}int i, count;int *list = grayCode(atoi(argv[1]), &count);for (i = 0; i < count; i++){printf("%d ", list[i]);}printf("\n");return 0;
}执行:
相关阅读:
Python 格雷码转换公式 i^i//2,简洁优美 pythonic_python 格雷码转数字
2. 矩阵问题
编写以下函数:
(1)在一个二维数组中形成以下形式的n阶矩阵:
[1 1 1 1 1
2 1 1 1 1
3 2 1 1 1
4 3 2 1 1
5 4 3 2 1]
```
(2)去掉靠边的元素,生成新的n-2阶矩阵;
(3)求生成的n阶矩阵主对角线上的元素之和;
(4)以方阵形式输出数组。
在main函数中调用以上函数进行测试。
**输入**
输入生成矩阵的阶数(n>=2)
**输出**
以方阵形式输出生成的n阶矩阵、去掉靠边的元素生成的新的n-2阶矩阵、以及生成的n阶矩阵主对角线上的元素之和,最后一行要回车
**样例输入**
```json
5
样例输出
Generated matrix:
1 1 1 1 1
2 1 1 1 1
3 2 1 1 1
4 3 2 1 1
5 4 3 2 1
del the elements on the side:
1 1 1
2 1 1
3 2 1
The sum of the diagonal:5
代码:(原题中的代码,已补充填空部分)
#include <iostream>
using namespace std;int main()
{while (1){int a;cin >> a;int array[a][a];for (int i = 0; i < a; i++)for (int j = 0; j < a; j++){if (j < i)array[i][j] = i + 1 - j;elsearray[i][j] = 1;}cout << "Generated matrix:" << endl;for (int i = 0; i < a; i++){for (int j = 0; j < a; j++){cout << array[i][j];}cout << endl;}cout << "del the elements on the side:" << endl;for (int i = 1; i < a - 1; i++){for (int j = 1; j < a - 1; j++){cout << array[i][j];}cout << endl;}int sum = 0;int i, j;for (i = a - 2, j = 1; i >= 1; i--, j++){sum += array[i][j];}cout << "The sum of the diagonal:" << sum << endl;}return 0;
}3. 搜索旋转排序数组 II
已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。
给你 旋转后 的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0 输出:true
示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3 输出:false
提示:
1 <= nums.length <= 5000-104 <= nums[i] <= 104- 题目数据保证
nums在预先未知的某个下标上进行了旋转 -104 <= target <= 104
进阶:
- 这是搜索旋转排序数组的延伸题目,本题中的
nums可能包含重复元素。 - 这会影响到程序的时间复杂度吗?会有怎样的影响,为什么?
代码:(原题中的代码,已补充填空部分)
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
static bool search(int *nums, int numsSize, int target)
{int lo = 0;int hi = numsSize - 1;while (lo <= hi){int mid = lo + (hi - lo) / 2;if (nums[mid] == target){return true;}if (nums[lo] == nums[mid] && nums[mid] == nums[hi]){lo++;hi--;}else if (nums[lo] <= nums[mid]){if (nums[lo] <= target && target < nums[mid]){hi = mid - 1;}else{lo = mid + 1;}}else{if (nums[mid] < target && target <= nums[hi]){lo = mid + 1;}else{hi = mid - 1;}}}return false;
}int main(int argc, char **argv)
{int i;int target = atoi(argv[1]);int size = argc - 2;int *nums = (int*)malloc(size * sizeof(int));for (i = 0; i < argc - 2; i++){nums[i] = atoi(argv[i + 2]);}printf("%d\n", search(nums, size, target));return 0;
}代码2:
#include <bits/stdc++.h>
using namespace std;class Solution {
public:bool search(vector<int> & nums, int target) {for (auto & num : nums)if (num == target) return true;return false;}
}; int main()
{Solution s;vector <int> nums = {2,5,6,0,0,1,2};cout << s.search(nums, 0) << endl;cout << s.search(nums, 3) << endl;return 0;
}输出:
1
0
相关文章:

C/C++每日一练(20230221)
目录 1. 格雷编码 2. 矩阵问题 3. 搜索旋转排序数组 II 1. 格雷编码 格雷编码是一个二进制数字系统,在该系统中,两个连续的数值仅有一个位数的差异。 给定一个代表编码总位数的非负整数 n,打印其格雷编码序列。即使有多个不同答案&#…...

用Python采集热门城市景点数据并简单制作数据可视化图
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 模块使用: 爬虫部分: requests parsel csv 数据分析部分: pandas pyecharts 如何安装模块: win R 输入 cmd 输入安装命令: pip install 模块名 回车 pycharm里面安装 terminal 输入安装命令…...

论文阅读:pixelNeRF: Neural Radiance Fields from One or Few Images
中文标题:从一或少量图像中构建神经辐射场 提出问题 NeRF效果虽然惊艳,但是其需要大量环绕图像以及长时间的训练。 创新点 与原始的NeRF网络不使用任何图像特征不同,pixelNeRF将与每个像素对齐的空间图像特征作为输入。也可以集合更多输入…...

C++项目——高并发内存池(1)--介绍及定长内存池
1.什么是内存池 1.1 池化技术 将程序中需要经常使用的核心资源先申请出来,放在一个池内,由程序自己管理,这样可以提高资源的使用效率,也可以保证本程序占有的资源数量。 比如之前博文实现的线程池,就是预先的申请出…...
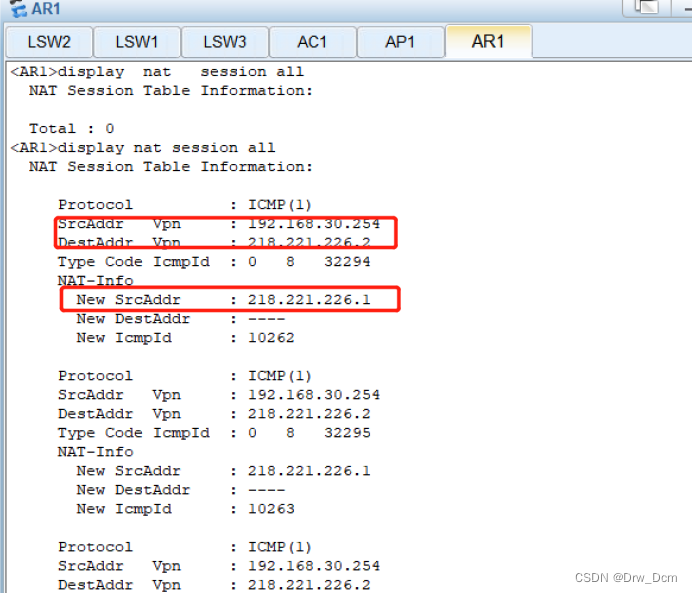
网络有线无线配置
一、需求 在无线接入区内,当Lsw1的上联口出现故障时,需要通过AP1-LSw1-LSw2-LSw3的路径访问公网server3。这是因为AP1通过无线网连接到LSw1,而LSw1与LSw3之间的链路出现故障,无法直接访问公网server3。因此,流量需要通…...

阅读笔记——Feature-Point Matching for Aerial and Ground Images方法
阅读笔记——Feature-Point Matching for Aerial and Ground Images 1.应用背景 在三维重建应用中,常用的是航空影像,但在城市环境中,面对大量的高层建筑物,航空影像往往不能很好的重建出完整的三维模型。因为航空影像视角约束以…...

前端工程师面试题10条必会笔试题
布局 左边20% 中间自适应 右边200px 不能用定位答案:圣杯布局/双飞翼布局或者flex什么叫优雅降级和渐进增强?渐进增强 progressive enhancement:针对低版本浏览器进行构建页面,保证最基本的功能,然后再针对高级浏览器进…...

【技术分享】Web自动化之Selenium安装
Web 应用程序的验收测试常常涉及一些手工任务,例如打开一个浏览器,并执行一个测试用例中所描述的操作。但是手工执行的任务容易出现人为的错误,也比较费时间。因此,将这些任务自动化,就可以消除人为因素。Selenium 可以…...
【Linux】进程状态的理解
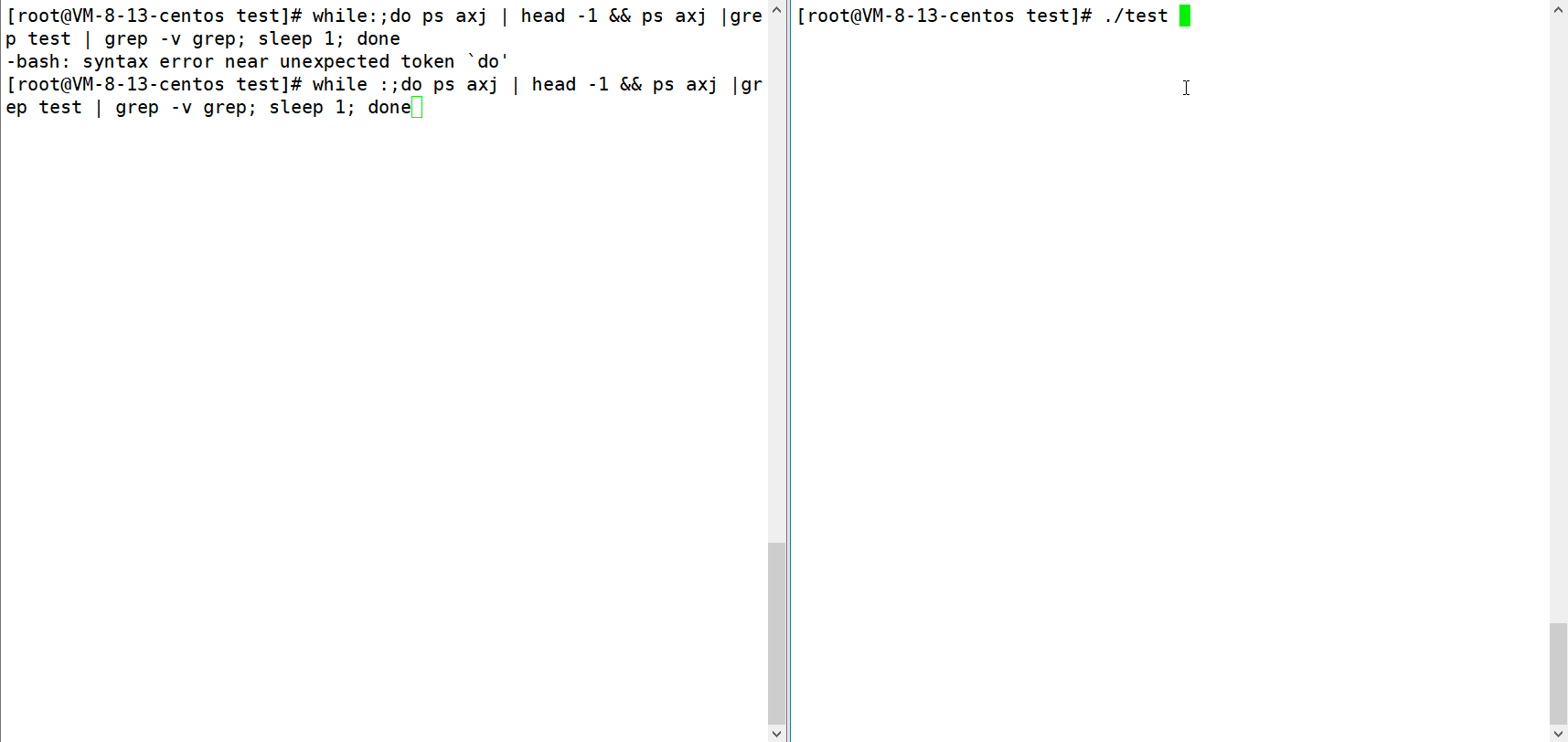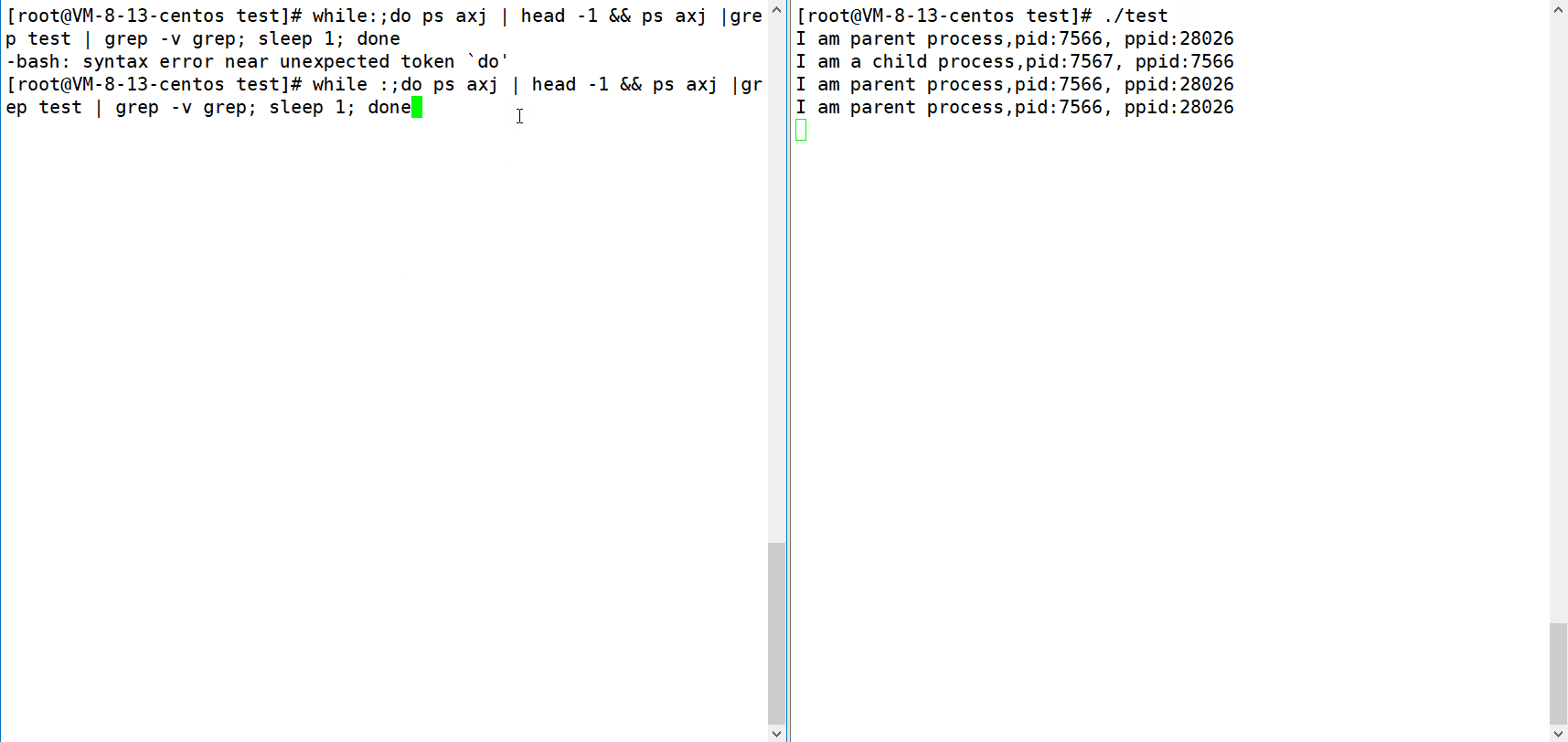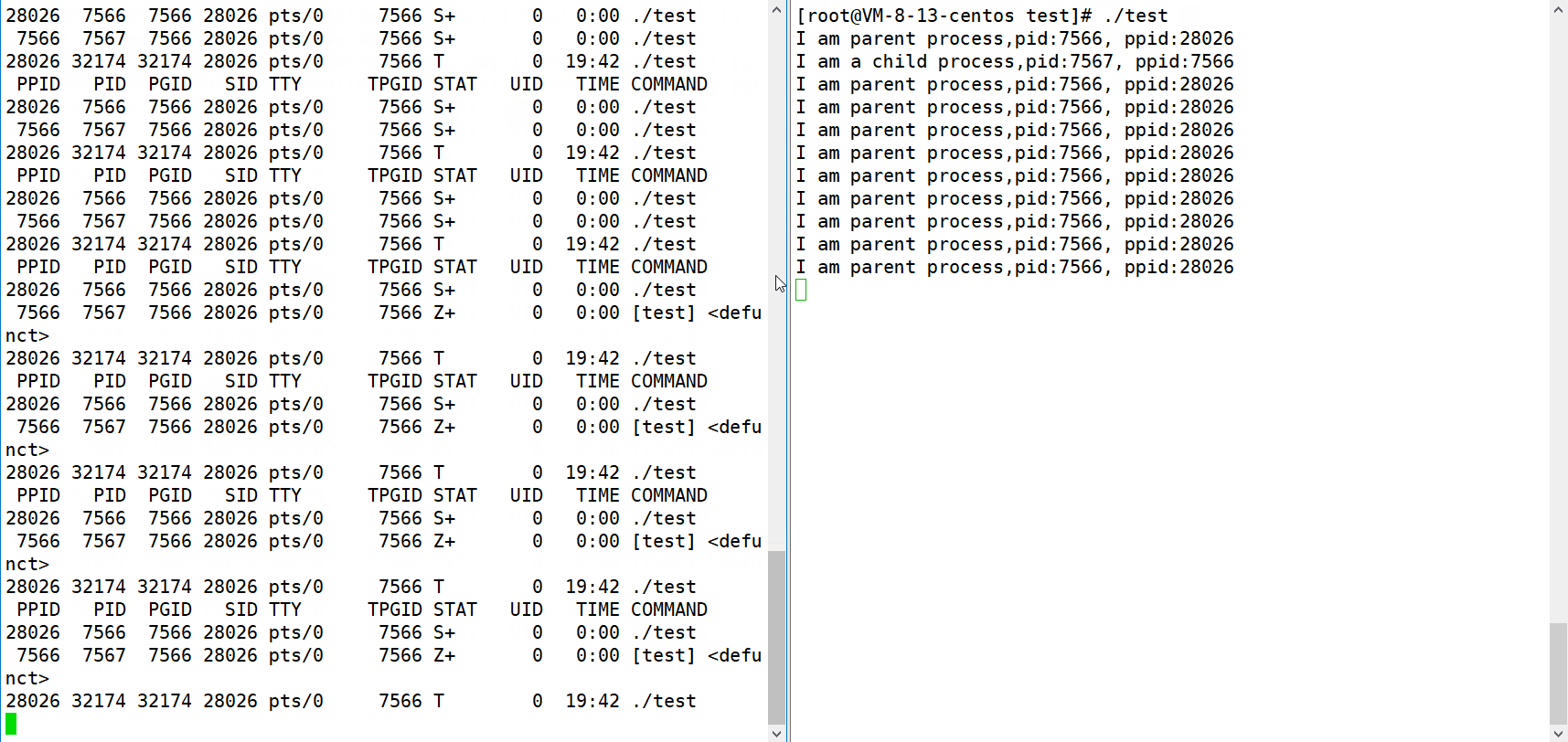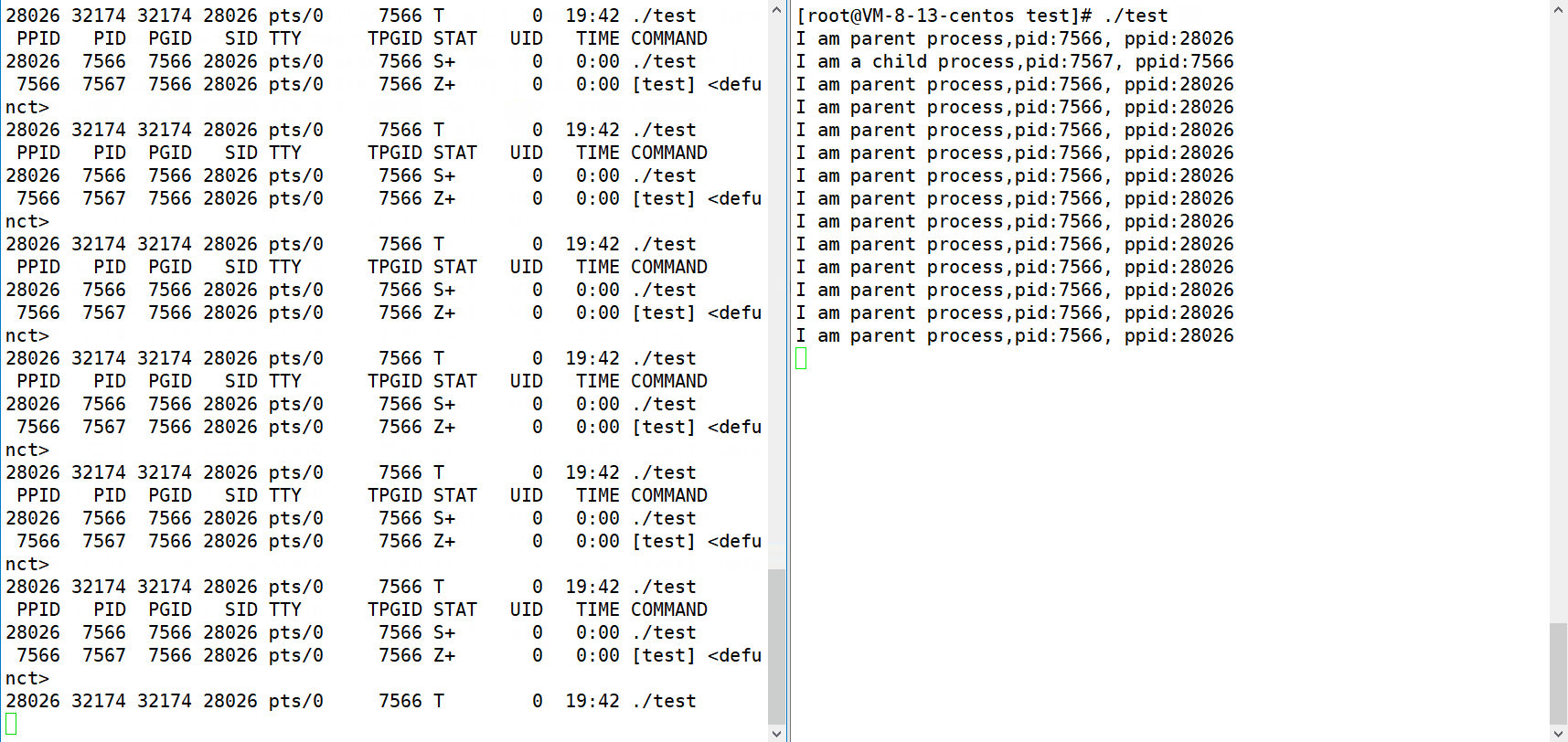
✍作者:阿润菜菜 📖专栏:Liunx系统编程 本文目录概述两个先行概念我们为啥创建进程Linux下的进程状态1. R 运行状态2.S 休眠状态 --- 可中断休眠状态3. D 磁盘休眠状态 ---不可中断休眠4.T 暂停状态 (t 追踪暂停状态)5…...

打游戏哪种蓝牙耳机比较好?适合玩游戏的无线蓝牙耳机
2023年耳机市场一如既往地卷,不只是卷音质,还在外观和功能上做了许多的改进,以至于现在哪怕不懂耳机的人从各电商平台都能闭眼入一个款平价品牌耳机且极少会踩雷,玩游戏是当前年轻人的娱乐方式,下面整理了几款适合玩游…...
Fortinet推出新一代自研安全芯片,跨所有网络边缘加速网络与安全融合
专注网络与安全融合的全球网络安全领导者 Fortinet(NASDAQ:FTNT),近日宣布推出新一代自研安全芯片 FortiSP5,作为 Fortinet ASIC 技术的最新突破,有力推动了分布式网络边缘安全的重大飞跃。FortiSP5 源自 F…...

ChatGPT爆火背后的真相:学编程已经成为必选项
这一阵最热门的话题,莫过于人工智能新选手——ChatGPT,在推出后只用了两个月就积累了1亿用户!它的出现在科技圈掀起了一阵“惊涛骇浪”,有人称ChatGPT的意义,堪比当年蒸汽机的出现,它足以爆发新一轮的“工业…...
Unity UI框架
一、简介 最近在各大网站看了一下 Unity3d 的 UI 框架,各种 UI 框架已经有很多的版本了,各有千秋,有的功能虽然写的完善,但用起来太复杂,有的框架功能不完善,搞个课程就上架了,还有什么 MVC 框…...

vue2提取vue-router的title单独存放,使用i18n实现
成品效果 首先引入i18n(vue-i18n官网文档) 依赖包 npm install vue-i18n8然后单独在src目录下新建一个文件夹lang,存放相对应的变量名称,我这里只做显示中文所以其他引入我都注释了,具体目录如下: src\lang/zh.js部分代码 export…...

【Linux操作系统】【综合实验三 用户帐号、文件系统与系统安全管理】
文章目录一、实验目的二、实验要求三、实验内容四、实验报告要求一、实验目的 要求掌握Linux系统用户的创建、删除与管理操作;熟悉Linux文件系统的管理模式,学会创建用户文件系统并装载和卸载文件系统;掌握超级用户的管理方式与权限…...
)
sqlite3数据库-sqlite语句1(五)
DML(Data Manipulation Language,数据操作语言) SELECT:查询表中的数据;SELECT语句中使用WHERE子句SELECT <列名>,... FROM <表名> WHERE <条件表达式>;SELECT id,name,purchase_price FROM Product; /*使用逗号分隔查询多列,顺序同子句顺序*/ SELECT * FROM…...
【图像分类】卷积神经网络之LeNet5网络模型实现MNIST手写数字识别
写在前面: 首先感谢兄弟们的关注和订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。 在上一篇博文中我们对LeNet5网络模型的结构进行了剖析,本篇博文,我们将使用PyTorch搭建LeNet5实现MNIST手写数字…...
前端开发环境搭建
文章目录Node.js是什么安装查看版本入门示例NPM使用 npm 命令安装模块常见命令使用淘宝 NPM 镜像TypeScript安装入门示例从github拉取构建项目如何从零创建一个TypeScript项目规划目录结构新建项目Web App运行服务添加依赖打包使用browserify打包使用webpack打包推荐流程目录配…...

学习Flask之四、网页表单
第二章介绍的request对象,使用了客户端请求的所有信息。特别地,request.form提供了对POST请求提交的表单数据的访问。尽管Flask请求对象的支持足于处理网页单,但是还有很多作务很繁锁和重复。两个很好的例子是产生HTML表单代码和验证表单数据…...
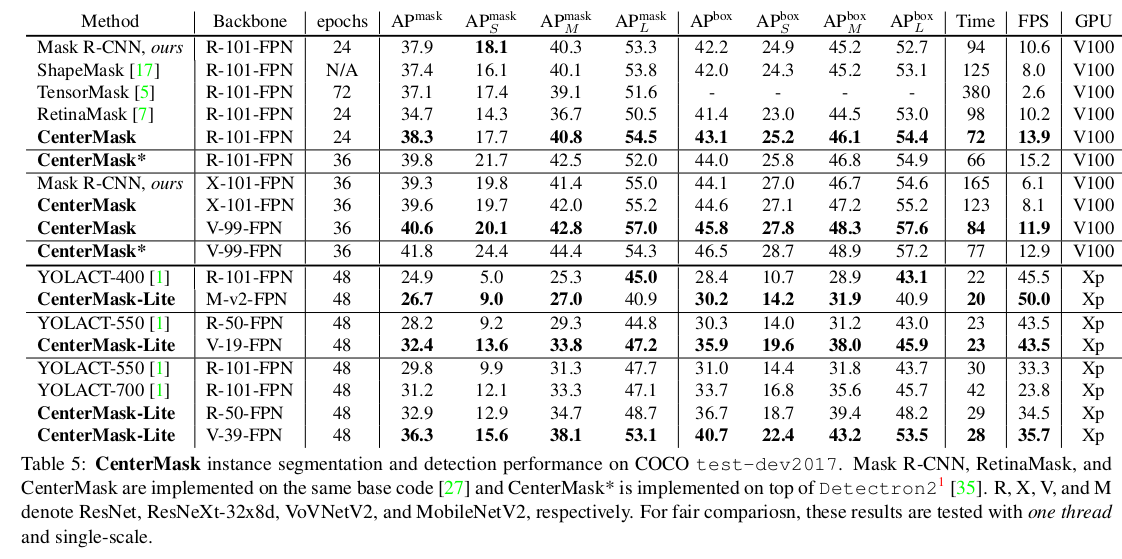
CenterMask paper笔记
CenterMask是一个anchor free的实例分割模型, 来自paper: CenterMask: Real-Time Anchor-Free Instance Segmentation 提起anchor free, 会想到FCOS模型,是用来目标检测的, 那么这里就用到了FCOS, 不过换了backbone, 在FCOS检测出目标框后&…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
