2023-9-2 Prim算法求最小生成树
题目链接:Prim算法求最小生成树

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 510, INF = 0x3f3f3f3f;int n, m;
int g[N][N];
int dist[N];
bool st[N];int prim()
{memset(dist, 0x3f, sizeof dist);int res = 0;for(int i = 0; i < n; i++){int t = -1;for(int j = 1; j <= n; j++)if(!st[j] && (t == -1 || dist[t] > dist[j]))t = j;if(i && dist[t] == INF) return INF;if(i) res += dist[t];for(int j = 1; j <= n; j ++) dist[j] = min(dist[j], g[t][j]);st[t] = true;}return res;
}int main()
{cin >> n >> m;memset(g, 0x3f, sizeof g);for(int i = 0; i < m; i++){int a, b, c;cin >> a >> b >> c;g[a][b] = g[b][a] = min(g[a][b], c);}int t = prim();if(t == INF) cout << "impossible" << endl;else cout << t << endl;return 0;
}
相关文章:

2023-9-2 Prim算法求最小生成树
题目链接:Prim算法求最小生成树 #include <iostream> #include <cstring> #include <algorithm>using namespace std;const int N 510, INF 0x3f3f3f3f;int n, m; int g[N][N]; int dist[N]; bool st[N];int prim() {memset(dist, 0x3f, size…...

骨传导耳机会影响听力吗?这是真的吗?
首先正常的使用骨传导耳机并不会影响我们的听力!那是为什么呢?? 因为骨传导是一种声音传导方式,可以通过人的颅骨、骨迷路、内耳淋巴液传递、螺旋器、听神经、听觉中枢来传递声波。 相对于通过耳道声波的经典声音传导方式&#x…...
【2023 B卷|100分】)
【华为OD机试python】 阿里巴巴找黄金宝箱(Ⅱ)【2023 B卷|100分】
题目描述 一贫如洗的樵夫阿里巴巴在去砍柴的路上,无意中发现了强盗集团的藏宝地, 藏宝地有编号从0-N的箱子,每个箱子上面贴有箱子中藏有金币的数量。 从金币数量中选出一个数字集合,并销毁贴有这些数字的每个箱子, 如果能销毁一半及以上的箱子,则返回这个数字集合的最小大…...

9.6 【C语言】使用枚举类型
如果一个变量只有几种可能的值,则可以定义为枚举类型,所谓“枚举”就是指把可能的值一一列举出来,变量的值只限于列举出来的值的范围内。 声明枚举类型用enum开头,例如: enum Weekday{sun,mon,tue,wed,thu,fri,sar};…...
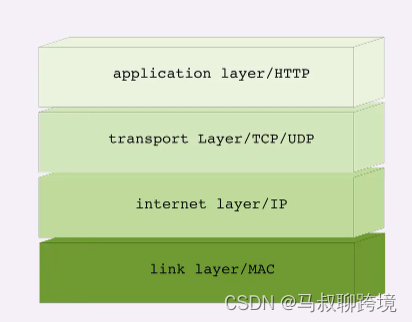
一文了解tcp/ip协议的运行原理
接触代理ip的人都了解https/sock5等ip协议,那么TCP/IP 协议又是什么? 一、什么是TCP/IP 协议? TCP/IP 协议实际上是一系列网络通信协议的一个统称,他负责具体的数据传输工作,核心的两个协议包括TCP以及IP,…...

spring cloud alibaba
项目依赖 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.2.5.RELEASE</version></parent><properties><springcloud.alibaba.version>2.1…...

K 次取反后最大化的数组和【贪心算法】
1005 . K 次取反后最大化的数组和 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以这种方式修改数组后,返回数组 可能…...

pulsar集群搭建_亲测成功
pulsar集群搭建_亲测成功 单机运行请看: Linux MacBook单机部署Pulsar并开启认证功能 集群组成 搭建 Pulsar 集群至少需要 3 个组件:ZooKeeper 集群、BookKeeper 集群和 broker 集群(Broker 是 Pulsar 的自身实例)。这三个集群组件如下: …...

笔记:linux中LED驱动设备树配置和用法
设备树中节点配置 设备树中的LED驱动一般是这样写,LED驱动可以控制GPIO的电平变化,生成文件节点很方便 leds: leds {compatible "gpio-leds";gpio_demo: gpio_demo {label "gpio_demo";gpios <&gpio0 RK_PC0 GPIO_ACTIV…...
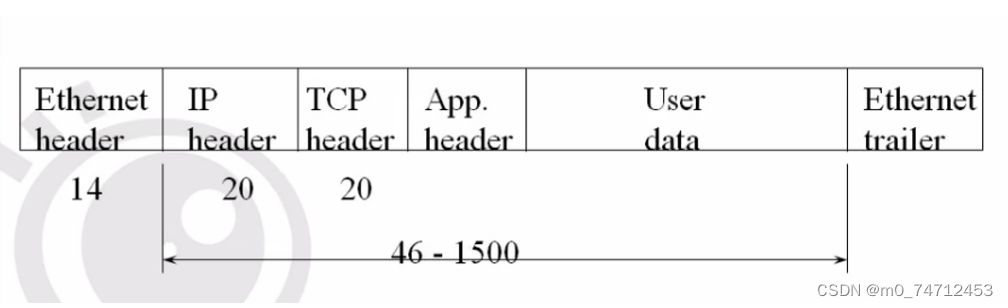
Linux网络编程 网络基础知识
目录 1.网络的历史和协议的分成 2.网络互联促成了TCP/IP协议的产生 3.网络的体系结构 4.TCP/IP协议族体系 5.网络各层的协议解释 6.网络的封包和拆包 7.网络预备知识 1.网络的历史和协议的分成 Internet-"冷战"的产物 1957年十月和十一月,前苏…...

盘点狼人杀中的强神与弱神 并评价操作体验
最初 强神是大家对猎人的称呼,但随着板子的增加 强神渐渐变成了强神神牌的统称。 狼人杀发展至今板子已经非常多了,而每个板子都会有不同的角色。 相同的是 大部分都会希望拿到一张强力神牌,这样能大大提高我们玩家的游戏体验,但其…...
)
数据结构与算法学习(day1)
前言 (1)我是一个大三的学生(准确来说应该是准大三,因为明天才报名哈哈哈)。 (2)最近就想每天闲着没事也刷些C语言习题来锻炼下编程水平,也一直在思考企业对应届大学生能力的要求,所以经常会想到关于面试的事情。由于我也没实习过,所以我对面试没有一个具象化的概念。…...

递归寻找第n位数字
编写递归函数digit(n,j),返回整数n的从右边开始的第j位数字 首先来看非递归法,只需用n/(10^(j-1))%10即可 #include<stdio.h> //编写递归函数digit(n,j),返回整数n的从右边开始的第j位数字 int digit(int n,i…...

[国产MCU]-W801开发实例-WiFi热点模式创建
WiFi热点模式创建 文章目录 WiFi热点模式创建1、创建WiFi热点相关API介绍2、热点创建实例W801的WiFi支持热点模式。本文将详细介绍如何创建热点模式。 1、创建WiFi热点相关API介绍 int tls_wifi_softap_create(struct tls_softap_info_t apinfo,struct tls_ip_info_t ipinfo)**…...

云原生Kubernetes:二进制部署K8S单Master架构(二)
目录 一、理论 1.K8S单Master架构 2.部署 master 组件 3.部署 Woker Node 组件 4.在master1节点上操作 5.在 node01 节点上操作 6.在 master01 节点上操作 7.在 node01 节点上操作 8.node02 节点部署(方法一) 二、实验 1.环境 2.部署 master …...
)
spring高级源码50讲-43-50(spring续)
其它 43) FactoryBean 演示 - FactoryBean 代码参考 package com.itheima.a43;import org.springframework.context.annotation.AnnotationConfigApplicationContext; import org.springframework.context.annotation.ComponentScan;ComponentScan public class A43 {publi…...
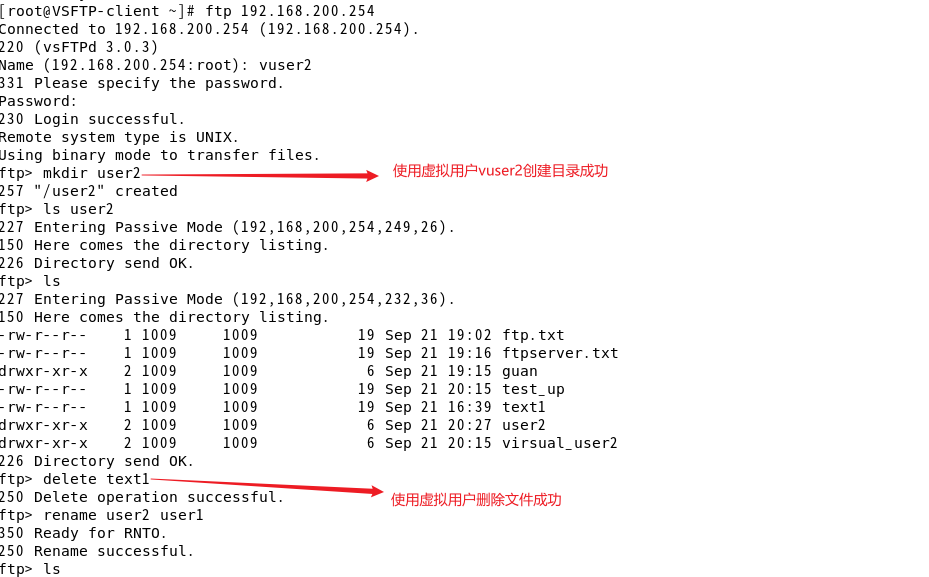
FTP文件传输服务器
目录 一、FTP协议两种工作模式 二、FTP数据两种传输模式 三、FTP用户分类 四、VSFTP配置案例 4.1匿名开放模式 4.2本地用户模式 4.3虚拟用户模式 五、实验总结 一、FTP协议两种工作模式 主动模式: 1、客户端主动向ftp服务器发送控制连接,三次握手控制连接…...
)
【LeetCode - 每日一题】2240. 买钢笔和铅笔的方案数(23.09.1)
2240. 买钢笔和铅笔的方案数 题意 两种价格的笔返回所有可以买的方案数可以为 0 解法 注意这道题的复杂度比较高,O(N2) 是过不了的。一开始是这样写的: // tle 代码 class Solution { public:long long waysToBuyPensPencils(int total, int cost1,…...
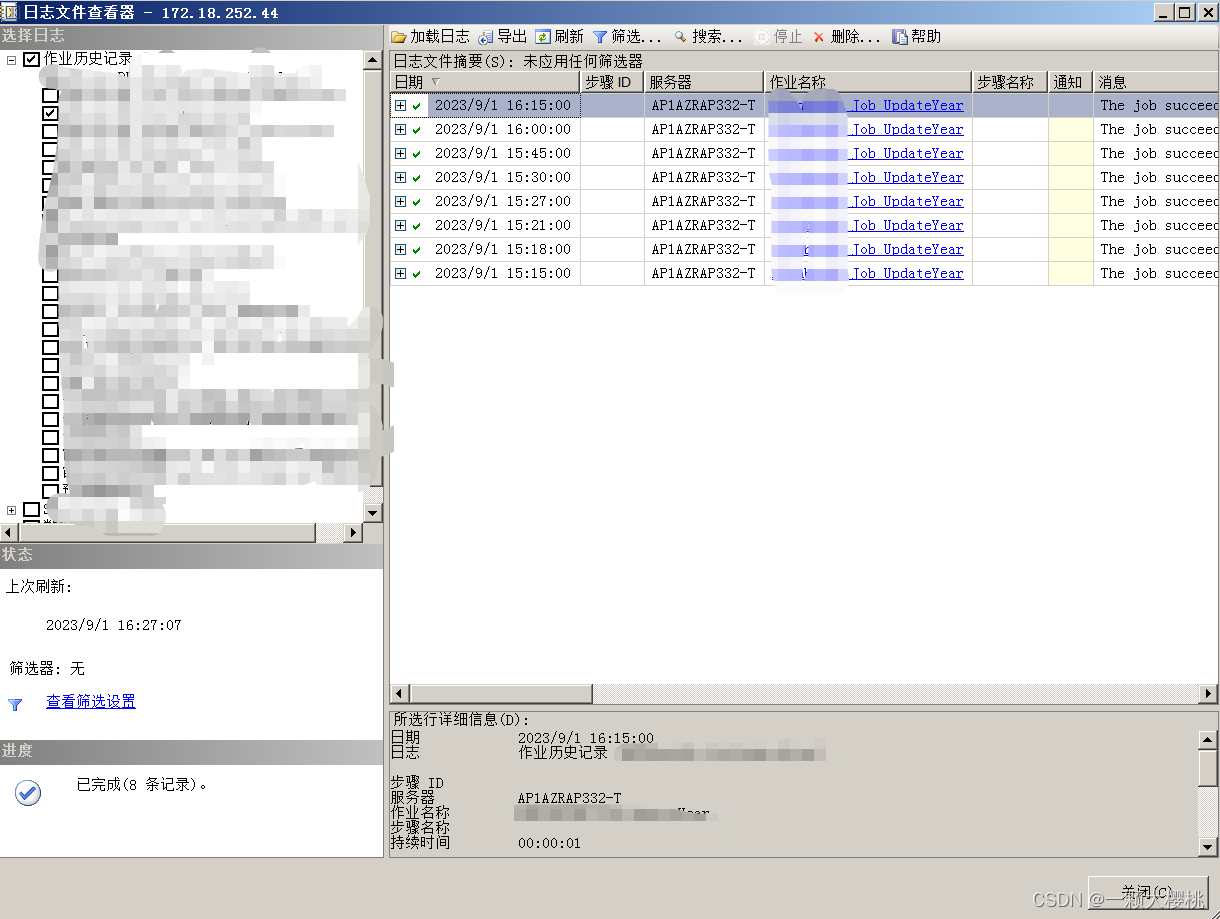
SQL Server如何新建作业
作业: 在 SQL Server 中,作业(Job)是一组可以在预定时间自动执行的任务。可以将作业看作是一个可以在后台运行的程序或脚本。作业由一系列步骤组成,每个步骤都是一个独立的任务,可以执行诸如执行 SQL 查询…...

【计算机网络】CDN 内容分发
CDN(Content Delivery Network)是一种用于加速网站内容传输的分布式网络架构。它的目标是通过在全球多个位置分布服务器来存储和分发网站的静态资源,从而减少用户访问这些资源的延迟,提高网站的加载速度和性能。以下是CDN内容分发…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
