layui实现数据列表的复选框回显
layui版本2.8以上
实现效果如图:
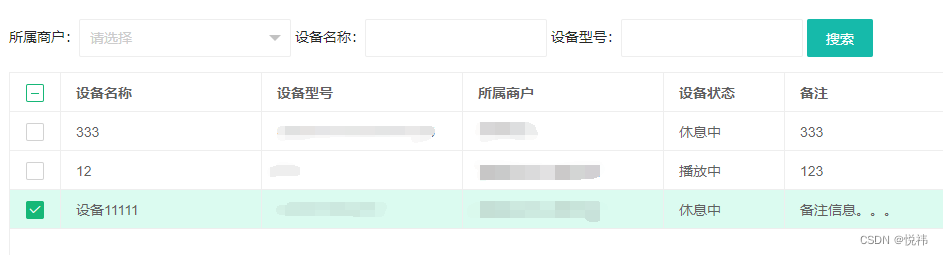
<input type="hidden" name="id" id="id" value="{:g_val( 'id',0)}">
<div id="tableDiv"><table class="layui-hide" id="table_list" lay-filter="table_list"></table>
</div><script src="layui/layui.js"></script>//方法级渲染table.render({elem: '#table_list', url: "/admin/****/****_search", cols: [[{type:'checkbox'},{field: 'name', title: '设备名称', width: 200}, {field: 'model_number', title: '设备型号', width: 200}, {field: 'merchant_name', title: '所属商户', width: 200}, {field: 'status', title: '设备状态', width: 120}, {field: 'remark', title: '备注', width: 200}, {field: 'create_time', title: '创建时间', width: 250}, {field: 'update_time', title: '更新时间', width: 250}]]// , page: true// , limit: 30// , height: document.documentElement.offsetHeight - 100, height: 'full-180' // 表格高度根据浏览器自适应, page: false// 取消分页时使用, limit: Number.MAX_VALUE// 取消分页时使用, done: function (res, curr, count) {$("[data-field='status']").children().each(function () {if ($(this).text() == '1') {$(this).text("播放中")} else if ($(this).text() == '2') {$(this).text("休息中")}});$("[data-field='deleted']").children().each(function () {if ($(this).text() == '1') {$(this).text("正常")} else if ($(this).text() == '0') {$(this).text("禁用")}});$.ajax({url: "/admin/****/get****",type: "post",data: { id: $('#id').val()},success: function (data) {//遍历ajax返回的结果//打印出data的格式为数组实例:[1,2,3,6]for (var i = 0; i < data.length; i++) {//遍历数据表格$.each(res.data, function (index, row) {//判断ajax返回的id是否与数据行中的id相等if (row.id == data[i]) {// console.log(row.LAY_INDEX);// console.log(row.LAY_TABLE_INDEX);$('#tableDiv tr[data-index=' + row.LAY_INDEX + '] input[type="checkbox"]').next().eq(0).click();$('#tableDiv tr[data-index=' + row.LAY_INDEX + '] input[type="checkbox"]').next().eq(1).click();}})}}});}});相关文章:

layui实现数据列表的复选框回显
layui版本2.8以上 实现效果如图: <input type"hidden" name"id" id"id" value"{:g_val( id,0)}"> <div id"tableDiv"><table class"layui-hide" id"table_list" lay-filter…...
关于使用RT-Thread系统读取stm32的adc无法连续转换的问题解决
关于使用RT-Thread系统读取stm32的adc无法连续转换的问题解决 今天发现rt系统的adc有一个缺陷(也可能是我移植的方法有问题,这就不得而知了!),就是只能单次转换,事情是这样的: 我在stm32的RT-T…...
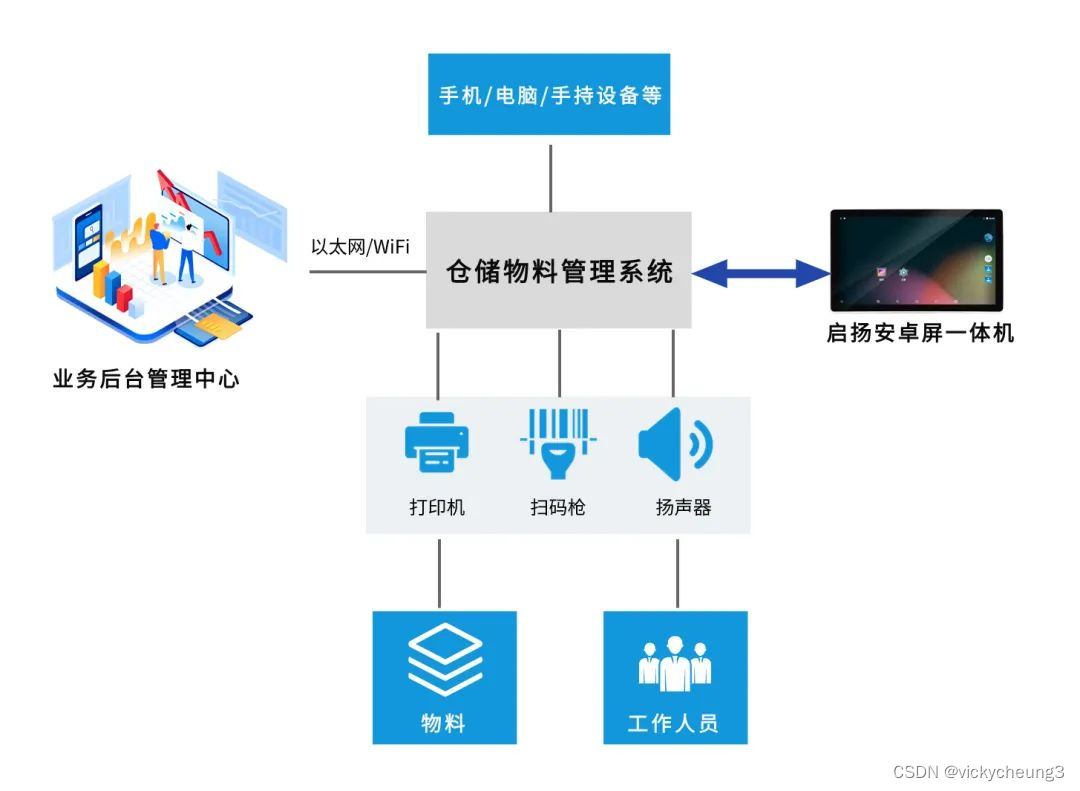
【启扬方案】启扬多尺寸安卓屏一体机,助力仓储物料管理系统智能化管理
随着企业供应链管理的不断发展,对仓储物料管理的要求日益提高。企业需要实时追踪和管理物料的流动,提高物流效率、降低库存成本和减少库存的风险。因此,仓储物料管理系统的实现成为必要的手段。 仓储物料管理系统一体机作为一种新型的物料管理…...

Android Glide使用姿势与原理分析
作者: 午后一小憩 简介 Android Glide是一款强大的图片加载库,提供了丰富的功能和灵活的使用方式。本文将深入分析Glide的工作原理,并介绍一些使用姿势,助你更好地运用这个优秀的库。 原理分析 Glide的原理复杂而高效。它首先基…...

管理类联考——逻辑——汇总篇——知识点突破——形式逻辑——联言选言——真假
角度——真值表 以上考点均是已知命题的真假情况做出的推理,还存在一种情况是已知肢判断P、Q的真假,断定干判断的真假,这种判断过程就是运用真值表。 P ∧ Q的真值 ①如何证明P ∧ Q为假? 由于P ∧ Q的本质是P、Q同时成立,所以只要P、Q有一个为假,整个命题就为假。 ②如…...
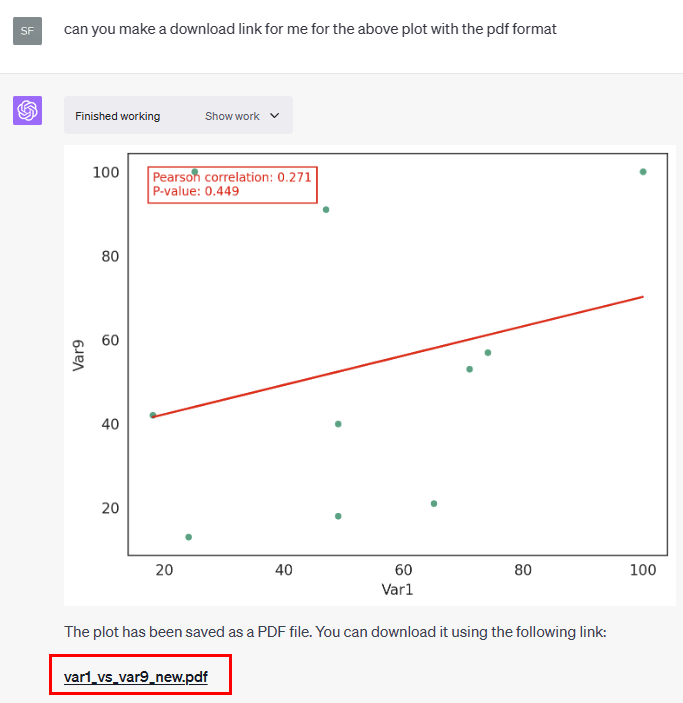
ChatGPT数据分析及作图插件推荐-Code Interpreter
今天打开chatGPT时发现一个重磅更新!code interpreter插件可以使用了。 去查看openai官网,发现从2023.7.6号(前天)开始,code interpreter插件已经面向所有chatGPT plus用户开放了。 为什么说code interpreter插件是一…...

说说FLINK细粒度滑动窗口如何处理
分析&回答 Flink的窗口机制是其底层核心之一,也是高效流处理的关键。Flink窗口分配的基类是WindowAssigner抽象类,下面的类图示出了Flink能够提供的所有窗口类型。 Flink窗口分为滚动(tumbling)、滑动(sliding&am…...
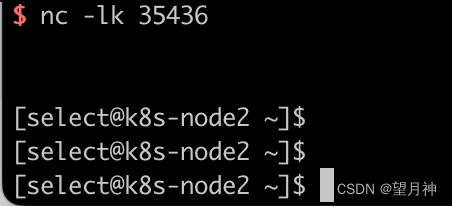
记一次反弹shell的操作【非常简单】
#什么是反弹shell 通常我们对一个开启了80端口的服务器进行访问时,就会建立起与服务器Web服务链接,从而获取到服务器相应的Web服务。而反弹shell是我们开启一个端口进行监听,转而让服务器主动反弹一个shell来连接我们的主机,我们再…...

如何排查 Flink Checkpoint 失败问题?
分析&回答 这是 Flink 相关工作中最常出现的问题,值得大家搞明白。 1. 先找到超时的subtask序号 图有点问题,因为都是成功没失败的,尴尬了。 借图: 2. 找到对应的机器和任务 方法很多,这里看自己习惯和公司提供…...
和c语言读日志文件筛选保存为新文件)
lazarus(pascal)和c语言读日志文件筛选保存为新文件
lazarus(pascal)和c语言读日志文件筛选保存为新文件,源于看日志每次从一个很多内容文件里查找不方便,写个代码输入时分秒参数,然后按行读取比较日志时间,当前秒和上一秒的输出保存为新文件,只保存2秒钟文件小多了&…...

学习JAVA打卡第四十九天
Random类 尽管可以使用math类调用static方法random()返回一个0~1之间的随机数。(包括0.0但不包括0.1),即随机数的取值范围是[0.0,1.0]的左闭右开区间。 例如,下列代码得到1~100之间…...
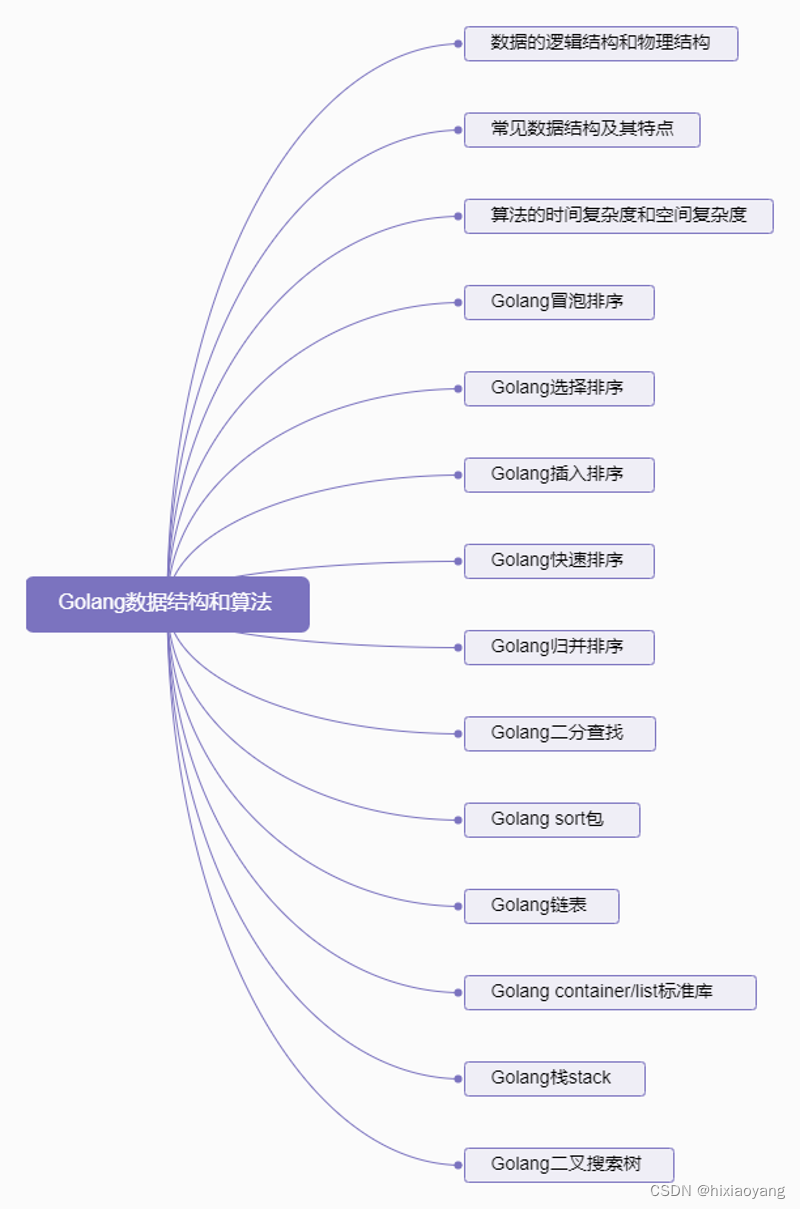
Golang数据结构和算法
Golang数据结构和算法 数据的逻辑结构和物理结构常见数据结构及其特点算法的时间复杂度和空间复杂度Golang冒泡排序Golang选择排序Golang插入排序Golang快速排序Golang归并排序Golang二分查找Golang sort包Golang链表Golang container/list标准库Golang栈stackGolang二叉搜索树…...

python 装饰器
装饰器是 Python 中一种功能强大的语法特性,它可以用于在不修改原函数代码的情况下,动态地扩展或修改函数的行为。装饰器本质上是一个函数或类,它接受一个函数作为参数,并返回一个新的函数或类。 下面是装饰器的详细解释和示例&a…...

iOS如何获取设备型号的最新方法总结
每一种 iOS 设备型号都有对应的一个或多个硬件编码/标识符,称为 device model 或者叫 machine name 通常的做法是,先获取设备的 device model 值,再手动映射为具体的设备型号(或者直接把 device model 值传给后端,让后…...

SpringBoot之RestTemplate使用Apache的HttpClient连接池
SpringBoot自带的RestTemplate是没有使用连接池的,只是SimpleClientHttpRequestFactory实现了ClientHttpRequestFactory、AsyncClientHttpRequestFactory 2个工厂接口,因此每次调用接口都会创建连接和销毁连接,如果是高并发场景下会大大降低性…...
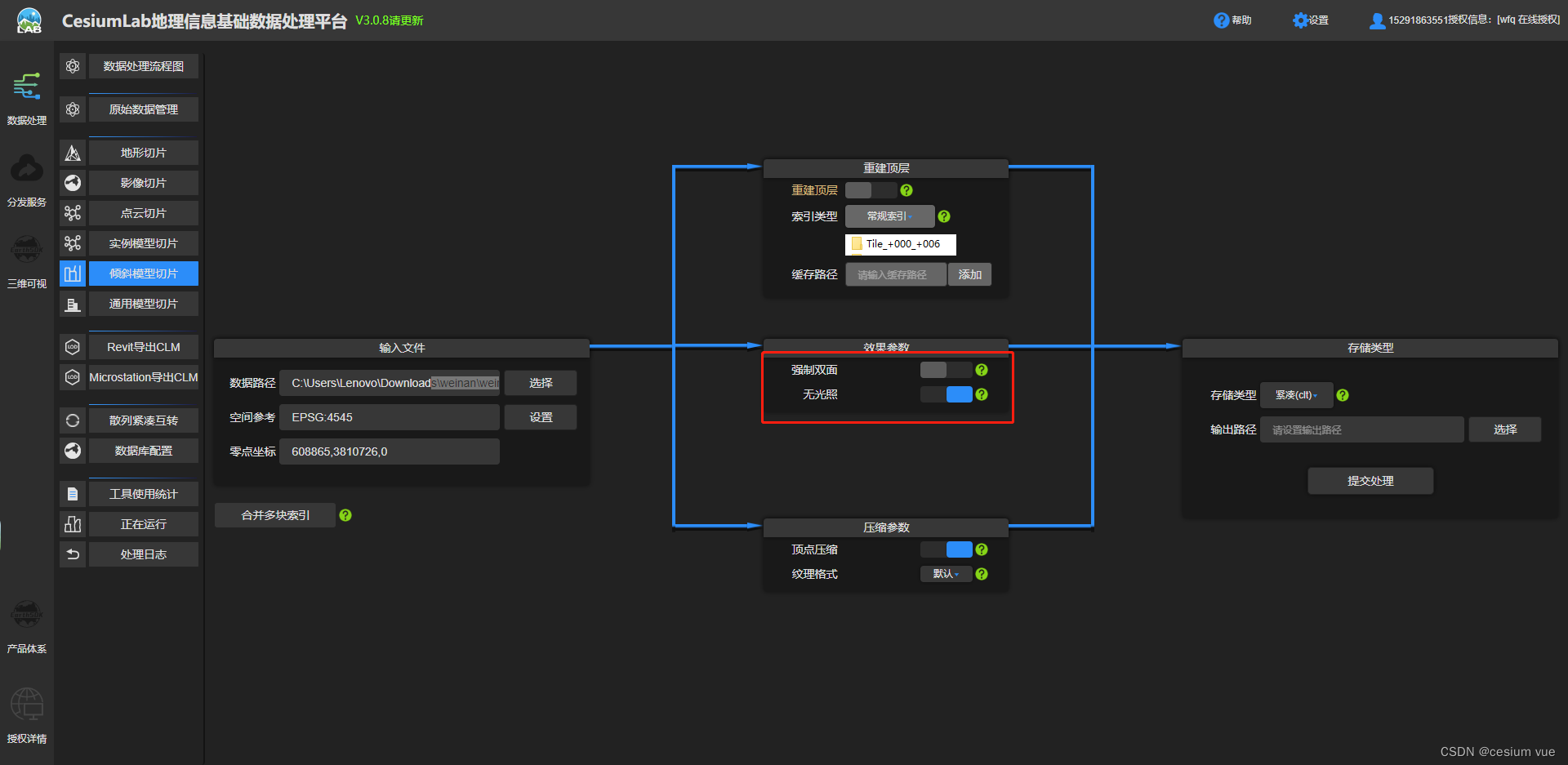
第49节:cesium 倾斜模型osgb转3dtiles,并加载(含源码+视频)
结果示例: 完整步骤: 1、启动并登陆cesiumlab 2、准备OSGB模型数据(含下载地址) 链接:https://pan.quark.cn/s/46ac7b0b2bed 提取码:TvWL3、倾斜模型切片 选择倾斜模型data文件夹 空间参考、零点坐标 默认 强制双面关闭、无光照 打开...

零信任安全模型详解:探讨零信任安全策略的原理、实施方法和最佳实践,确保在网络中实现最小特权原则
在当今日益复杂和危险的网络环境中,传统的网络安全模型已经不再能够满足对抗不断进化的威胁。零信任安全模型应运而生,以其强调“不信任,始终验证”的理念,成为了当今信息技术领域中的热门话题。本文将深入探讨零信任安全模型&…...

01_nodejs简介
01 【nodejs简介】 1.前言 Node 的重要性已经不言而喻,很多互联网公司都已经有大量的高性能系统运行在 Node 之上。Node 凭借其单线程、异步等举措实现了极高的性能基准。此外,目前最为流行的 Web 开发模式是前后端分离的形式,即前端开发者…...
企业架构LNMP学习笔记4
企业服务器LNMP环境搭建: 常见的软件架构: 1)C/S: client/server 2)B/S: browser/server 不管是C还是B,都是属于客户端属于前端。那么运维人员主要是负责和管理的Server端,也统称为服务器端。为了快速的…...

探索UniApp分包
目录 什么是UniApp分包? UniApp分包的原理 优势 如何使用UniApp分包 1.manifest.json文件配置 2.静态图片资源分包注意事项 3.pages.json配置 结论 探索UniApp分包:优化移动应用性能与用户体验 在移动应用开发领域,性能和用户体验是至…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
