树与图c++
1.树
前言
本文主要介绍的数据结构之树型结构的相关知识,树型数据结构是面试官面试的时候非常喜欢考的一种数据结构,树形结构的遍历也是大厂笔试非常喜欢设置的考点,这些内容都会在本篇文章中进行详细的介绍,并且还会介绍一些常用的算法。
一、树的基本概念
层次结构的数据在现实世界中大量存在。例如,一个国家有若干省,一个省有若干市县,一个市县有若干区乡。又如,一本书包含若干章,一章包含若干节,一节包含若干段。例如,下图是数组的层次关系,这种描述树形数据的形式称为倒置的树形表示法。
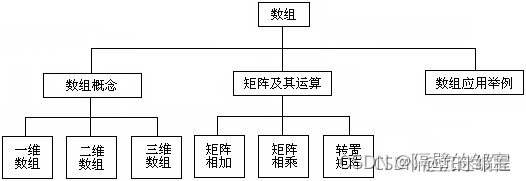
线性数据结构一般不适合用来表示层次数据。为了组织层次数据,需要对树形数据的结构进行研究。
1.1树的定义
在上图1中,我们采用倒置树来描述树状结构。一棵倒置树的顶端是根,根有几个分枝,称为子树,每棵子树再分成几个小分枝,小分枝再分成更小的分枝,每个分枝也都是树,一个结点也是树。由此,我们可以给树下一个递归定义。
树(Tree)是包括n个结点的有限非空集合T,其中,一个特定的结点r称为根(Root),其余结点T-{r}划分成m个互不相交的子集T1,T2,Tm其中,每个子集都是树,称为树根r的子树。
根据树的定义,一个结点的树是仅有根结点的树,这时m=0,这棵树没有子树。
1.2基本术语
图1可以抽象成图2,它形象地反映了树的逻辑结构。下面,参照图2,给出树结构讨论中常用的术语。
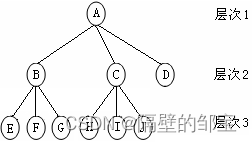
树中元素称为结点(Node),如A、B等。
如果某结点到另一结点之间存在着连线,则称此连线为一条边(Edge),如<A,B>、<B,E>等。
如果从某个结点沿着树中的边可到达另一个结点,则称这两个结点间存在一条路径(Path),如结点A到结点J,存在路径{<A,C>,<C,J>}。
如果一个结点有子树,则称该结点为子树的双亲(Parent),子树的根称为该结点的孩子(Child),如结点A是结点B、C、D的双亲,而结点B、C、D是结点A的孩子。具有相同双亲的结点称为兄弟(Sibling),如结点B、C、D是兄弟。
结点拥有的子树数目称为结点的度(Degree),如结点A的度为3,结点D的度为0,结点J的度为0。
度为零的结点称为叶子(Leaf)。
规定根结点的层次为1,树中结点的最大层次称为该树的高度(Hight),如图2所表示的树的高度为3。
如果树中结点的各子树是从左至右有次序的,则称该树为有序树,否则称为无序树。
二、二叉树
树结构和自然界的树一样,具有各种各样的形态,这样就使我们对树结构的研究比较困难。为此,我们首先研究最为常见的二叉树,以及二叉树的性质、存储结构和运算,然后给出二叉树和一般树之间的转换。
2.1二叉树的定义
二叉树(Binary Tree)是由有限个结点组成的集合,它或者为空集合,或者仅含一个根结点,或者由一个根结点和两棵互不相交的左、右子树组成。
上述定义表明,二叉树有如图3所示的五种基本形态。
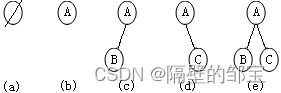
必须指出,树定义与二叉树定义稍有区别。首先,树不能是空树,却可以有空二叉树。其次,一般树的子树的不分次序,而二叉树的子树却分左、右子树,即使在仅有一棵子树的情况下也要指明是左子树还是右子树。最后,一般树中结点的度(子树数目)可以大于2,但二叉树中结点的度均不超过2。
2.2二叉树的性质
若二叉树高为h,树的结点总数为2^h-1,称此二叉树为满二叉树。
h=3,那么结点总数7(包含根节点)
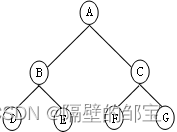
【性质1】高度为h的二叉树的结点总数n<=2^h-1。
这个性质很容易理解:
证明:对于高度为h的满二叉树,其结点总数为
它是高度为h的二叉树结点总数的最大值,故。
对于高度为h的二叉树,如果第1~h-1层构成满二叉树,而第h层的叶子结点严格按从左至右依次排列,称此二叉树为完全二叉树(如图5(a)所示)。
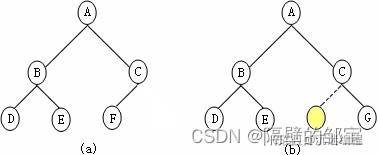
在图5(b)中,双亲结点C仅有右孩子G无左孩子,故它不是完全二叉树。
【性质2】对于含n(n>=1)个结点的完全二叉树(区分满二叉树),其高度 h = ⌈ l o g 2 ( n + 1 ) ⌉ h=\lceil log2(n+1) \rceil h=⌈log2(n+1)⌉ 。
eg:上述图a,n=6,那么
h = [ l o g 2 ( 6 + 1 ) ] = l o g 2 ( 8 ) = 3 h=[log2(6+1)]=log2(8)=3 h=[log2(6+1)]=log2(8)=3
【性质3】对于一棵非空二叉树,如果度为0的结点数为,度为2的结点数为,则
=+1。 (即零度结点数总比2度结点数大1)
证 设二叉树的结点数为n,度为1的结点数为n1,边数为e,则
e = n − 1 e=n-1 e=n−1
e = 2 × n 2 + n 1 e=2×n2+n1 e=2×n2+n1
n = n 0 + n 1 + n 2 n=n0+n1+n2 n=n0+n1+n2
边数等于结点数n-1 ,等于2倍的度为2的结点数+度为1的结点数。
画个树的逻辑结构图就很容易看出来。
于是n0=n2+1。
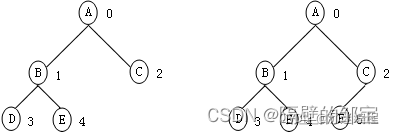
【性质4】对于含个结点的完全二叉树(区分满二叉树),按从上到下、从左到右的顺序,从0到n-1编号(如图6所示)。对于树中编号为 i ( 0 = < i < = n − 1 ) i(0=<i<=n-1) i(0=<i<=n−1)的结点,有
(1)如果 i = 0 i=0 i=0,则该结点为二叉树的根;
(2)如果 2 i + 1 < n 2_i+1<n 2i+1<n,则其左孩子为 2 i + 1 2_i+1 2i+1,否则不存在左孩子;
(3)结点的双亲为[(i-1)/2]向下取整。(求双亲注意双亲只有一个)
2.3二叉树的ADT
ADT BinTree
数据:
0个或有限个结点组成的集合。
运算:
Create()
创建一棵空二叉树或二叉树。
IsEmpty()
若二叉树为空,则返回1,否则返回0。
PreOrder()
前序遍历二叉树。
InOrder()
中序遍历二叉树。
PostOrder()
后序遍历二叉树。
Display():
输出二叉树。
三、二叉树的存储表示
3.1二叉树的数组表示
用一维数组来存储二叉树,首先将二叉树想象成一棵完全二叉树,对于没有左孩子或右孩子的结点,用特殊字符(或数字)替代,再依从上至下、从左至右的次序,依次将结点值存放到一维数组之中。
【例1】:将图7(a)所示的二叉树,用一维字符数组表示。
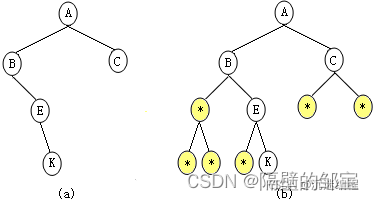
解:
首先将图7(a)所示的二叉树,想象成一棵完全二叉树(如图7(b)所示),再用表8-1所示的一维字符型数组存储。
这种表示法的实现程序如下:示法的实现程序如下:
#include <bits/stdc++.h>
using namespace std;
const int MaxSize 64//为了树的显示效果,结点数不超过63,即二叉树高不超过6
//创建二叉树
void Create(char Node[], int& n)
{cout << "按完全二叉树输入结点字符,空字符用替代" << endl;cin >> Node;//计算字符数组含字符个数n = 0;while (Node[n] != '\0')//当Node[n]不等于结束符时n++;
}
//输出二叉树
void Display(char Node[], int n)
{int hight, layer, num; //hight树高,layer树层,num结点编号hight = ceil(log(n + 1) / log(2));//确定完全二叉树高度//求下限接近整数ceil//自然对数 log//求上限接近整数 floorcout << hight << endl;num = 0;//从结点Node[0]开始输出for (layer = 1; layer <= hight; layer++)//输出1层—hight层{ //每层前面空格的输出控制for (int i = 1; i <= pow(2, hight - layer)-1; i++)cout << " ";//每层结点的输出控制for (int j = 1; j <= pow(2, layer - 1); j++, num++){if (Node[num] != '' && Node[num] != '\0')cout << Node[num];//遇到结点,输出结点else if (Node[num] == '')cout << " ";//遇到号,输出空格elsebreak;//遇到结束符,跳出输出//每层结点间空格的输出控制for (int k = 1; k <= pow(2, hight - layer + 1) - 1; k++)cout << " ";}cout << endl;//输完一层,换行}
}
//主函数
int main()
{int n;//完全二叉树所含结点数char Node[MaxSize];//定义字符型的结点数组Create(Node, n);//创建二叉树结点的一维数组cout << "二叉树为" << endl;Display(Node, n);//输出二叉树return 0;
}
程序运行的结果如图8所示:
创建这棵5结点二叉树,用了6颗星号替代缺失的左、右孩子,这显然是这种表示法的一个缺点。
但当二叉树为完全二叉树时,该表示法具有建树简便,输出直观的优点。
3.2二叉树的链表表示
用一维数组表示的二叉树,不便实现二叉树的一些规定运算。因此,二叉树一般采用链表来创建。
链式二叉树结点的逻辑结构如图9所示,其中,data用来存储结点值,*lChild、*rChild分别用来存储左、右孩子的地址。
图9 树节点的逻辑结构
【例2】创建图7(a)所示的链式二叉树。
用链表表示图7(a),其逻辑结构如图10所示,其中Λ代表NULL。
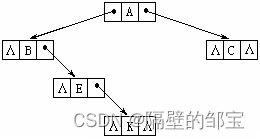
具体的创建过程如下:
(1)首先创建第4层结点,并用结点指针Kp指向其根结点,如图11所示。
图11
(2)再创建第3层结点,并用结点指针Ep指向其根结点,如图12所示。
图12
(3)再创建第2层结点,并用结点指针Bp、Cp分别指向其根结点,如图13所示。
图13
(4)最后创建第1层结点,并用结点指针Ap指向其根结点,如图14所示。
图14
如果用程序来描述上述过程,其程序如下:
#include<iostream>
using namespace std;
//二叉树结点定义
struct Node
{ char data;//数据域Node *lChild,*rChild;//指针域
};
//二叉树定义
struct BinTree
{ Node *root;
};
//创建二叉树
void Create(BinTree &T,char x,Node *left,Node *right)
{ Node *NewNode;//新结点NewNode=new Node;//为新结点申请内存NewNode->data=x;//为新结点数据域赋值NewNode->lChild=left;//为新结点左指针域赋值NewNode->rChild=right;//为新结点右指针域赋值T.root=NewNode;//让新结点成为该子树根结点
}
//主函数
int main()
{ BinTree K,E,B,C,A;Create(K,'K',NULL,NULL);//创建结点K的子树Create(E,'E',NULL,K.root);//创建结点E的子树Create(B,'B',NULL,E.root);//创建结点B的子树Create(C,'C',NULL,NULL);//创建结点C的子树Create(A,'A',B.root,C.root);//创建结点A的子树return 0;
}
上述链式二叉树的创建过程是,先创建最底层的叶子结点,然后向上逐层创建子树,直至最顶层的根结点。该方法的优点是直观易懂,缺点是无法给出通用程序。一般链式二叉树的创建方法与通用程序如下。
用广义表构建二叉树。
- 二叉树的广义表表示法
尽管构建二叉树的方法并不复杂,但对于结点多、结构复杂的二叉树,却不易用程序来实现。因此,有必要寻找更具一般性的二叉树的构建方法。
图1所示的二叉树,可以用以下方式重新表示它。
用A(B)表示A有左孩子B,无右孩子;
用B(C,D)表示B有左孩子C,右孩子D;
用C(,E)表示C无左孩子,但有右孩子E;
用D(F,G)表示D有左孩子F,右孩子G。
将它们复合起来,有A(B(C(,E),D(F,G)))。这是一个字符数组,它是上述二叉树的另一种表示法,称这种二叉树的表示法为广义表法。
用广义表来表示二叉树,其具体规定如下:
树的根结点放在最前面。
每个结点的左子树和右子树用逗号隔开。若仅有左子树没有右子树,逗号可省略;若仅有右子树没有左子树,逗号不能省略。
约定,广义表用字符型数组 GenList[] 来存储。
- 广义表构建二叉树的算法
设结点值均用字母来替代,先建一棵空二叉树T,借助一个简易结点顺序栈 stack ,广义表A(B(C(,E),D(F,G)))创建二叉树的具体过程如下:
(1)读A,创建新结点A,T为空,让T.root=A结点。
(2)读(,让新结点A入栈,置k=1,栈stack状态为:
A
(3)读B,创建新结点B,因k=1,让栈顶结点A的左指针指向B,即B←A。
(4)读(,让新结点B入栈,置k=1,栈stack状态为:
A
B
(5)读C,创建新结点C,因k=1,让栈顶结点B的左指针指向C,即C←B。
(6)读(,让新结点C入栈,置k=1,栈stack状态为:A B C
(7)读,号,置k=2。
(8)读E,创建新结点E,因k=2,让栈顶结点C的右指针指向E,即C→E。
(9)读),栈顶结点C出栈,栈stack状态为:A B
(10)读,号,置k=2。
(11)读D,创建新结点D,因k=2,让栈顶结点B的右指针指向D,即B→D。
(12)读(,让新结点D入栈,置k=1,栈stack状态为:A B D
(13)读F,创建新结点F,因k=1,让栈顶结点D的左指针指向F,即F←D。
(14)读,号,置k=2。
(15)读G,创建新结点G,因k=2,让栈顶结点D的右指针指向G,即D→G。
(16)读),栈顶结点D出栈,栈stack状态为:A B
(17)读),栈顶结点B出栈,栈stack状态为:A
(18)读),栈顶结点A出栈,栈stack状态为:
至此,二叉树创建完毕。
由T.root=A,B←A,C←B,C→E,可构建如下图2所示的二叉树。
图2 二叉树的构建过程1
由B→D,F←D,D→G,可构建如图3所示的二叉树。
图3 二叉树的构建过程2
3. 广义表构建二叉树算法的程序实现
#include<iostream>
using namespace std;
const int MaxSize 100//顺序栈的最大容量
//结点定义
struct Node
{ char data;//数据域Node *lChild,*rChild;//指针域
};
//二叉树定义
struct BinTree
{ Node *root;
};
//创建空二叉树
void Create(BinTree &T)
{ T.root=NULL;
}
//树判空
int IsEmpty(BinTree T)
{ if(T.root==NULL) return 1;else return 0;
}
//广义表创建二叉树
void Create(char GenList[],BinTree &T)
{ Node *stack[MaxSize],*NewNode,*p;//简易结点顺序栈,新结点,探测指针int top=-1;//置栈空int k,i=0;//k=1链接左子树,k=2链接右子树,i广义表字符下标char ch;do{ ch=GenList[i];//读取广义表第i个字符switch(ch){ case '('://读到左括号stack[++top]=NewNode;//新结点入栈k=1;break;case ')'://读到右括号top--;break;//栈顶结点出栈case ','://读到逗号k=2;break;default://读到字符NewNode=new Node;//新结点申请内存NewNode->data=ch;//新结点数据域赋值NewNode->lChild=NULL;//新结点左指针域赋值NewNode->rChild=NULL;//新结点右指针域赋值if(IsEmpty(T))//如果树为空T.root=NewNode;//新结点作为根结点if(k==1){ p=stack[top];//获取栈顶结点p->lChild=NewNode;//让栈顶结点左孩子指向新结点}else if(k==2){p=stack[top];//获取栈顶结点p->rChild=NewNode;//让栈顶结点左孩子指向新结点}}i++;//i增1}while(GenList[i]!='\0');//逐一读完整个广义表
}
//非递归前序遍历算法
void PreOrder(Node *p)
{ Node *stack[MaxSize];// 简易结点顺序栈int top=-1;//置栈空while(p||top!=-1)//当p结点所指非空或栈非空时{ if(p)//如果p所指结点非空{ cout<<p->data;//输出p的值stack[++top]=p;//p所指结点入栈p=p->lChild;//p向左下移}else//如果p结点所指结点为空{ p=stack[top--];//p指向栈顶结点,栈顶结点出栈p=p->rChild;//p向右下移}}
}
//非递归中序遍历算法
void InOrder(Node *p)
{ Node *stack[MaxSize];//简易结点顺序栈int top=-1;//置栈空while(p||top!=-1)//当p结点所指非空或栈非空时{ if(p)//如果p所指结点非空{ stack[++top]=p;//p所指结点入栈p=p->lChild;//p向左下移}else//如果p所指结点为空{ p=stack[top--];//p指向栈顶结点,栈顶结点出栈cout<<p->data;//输出p的值p=p->rChild;//p向右下移}}
}
//主函数
int main()
{ char GenList[]="A(B(C(,E),D(F,G)))";//定义广义表BinTree T;//定义二叉树Create(T);//创建空二叉树Create(GenList,T); //创建二叉树cout<<"前序遍历为 "; PreOrder(T.root); cout<<endl;cout<<"中序遍历为 "; InOrder(T.root); cout<<endl;return 0;
}
程序运行的结果如图4所示。
图4
四、二叉树的遍历
欲在屏幕上形象地输出链式二叉树是一件困难的事,一般采用输出它的三个线性序列VLR、LVR和LRV的方式,来解决这一问题。
VLR称为前序(PreOrder)遍历序列,它是按先树根,再左子树,后右子树的次序,输出二叉树的结点值。
LVR称为中序(InOrder)遍历序列,它是按先左子树,再树根,后右子树的次序,输出二叉树的结点值。
LRV称为后序(PostOrder)遍历序列,它是按先左子树,再右子树,后树根的次序,输出二叉树的结点值。
所谓前序、中序和后序遍历,是相对于根结点位置而言的。例如,在中序遍历中,根结点在中间;而前序遍历是根结点在前面,后序遍历是根结点在后面。三种遍历方式一定是先左子树后右子树。
4.1前序遍历
前序遍历的次序为:树根—左子树—右子树,即从根结点开始处理,根结点处理完后往左子树走,直到无法前进再处理右子树。
图10 链式二叉树的逻辑结构
【例2】的前序遍历为ABEKC,前序遍历的递归算法如下:
void PreOrder(Node *p)
{ if(p!=NULL){ cout<<p->data;//访问树根PreOrder(p->lChild);//遍历左子树PreOrder(p->rChild); //遍历右子树}
}
4.2中序遍历
中序遍历的次序为:左子树—树根—右子树,即沿树的左子树一直往下,直到无法前进时后退到双亲结点,而后再沿右子树一直往下。如果右子树也走完了就退回上层的左结点,重复左、中、右的顺序遍历。
【例2】的中序遍历为BEKAC,中序遍历的递归算法如下:
void InOrder(Node *p)
{ if(p!=NULL){ InOrder(p->lChild); //遍历左子树cout<<p->data; //访问树根InOrder(p->rChild);//遍历右子树}
}
【例2】的后序遍历为KEBCA,后序遍历的递归算法如下:
void PostOrder(Node *p)
{ if(p!=NULL){ PostOrder(p->lChild);//遍历左子树PostOrder(p->rChild); //遍历右子树cout<<p->data; //访问树根}
}
#include<iostream>
using namespace std;
//二叉树结点定义
struct Node
{char data;//数据域Node* lChild, * rChild;//指针域
};
//二叉树定义
struct BinTree
{Node* root;
};
//创建二叉树
void Create(BinTree& T, char x, Node* left, Node* right)
{Node* NewNode;//新结点NewNode = new Node;//新结点申请内存NewNode->data = x;//新结点数据域赋值NewNode->lChild = left;//新结点左指针域赋值NewNode->rChild = right;//新结点右指针域赋值T.root = NewNode;//让新结点成为该子树根结点
}
//前序遍历
void PreOrder(Node* p)
{if (p != NULL){cout << p->data;//访问树根PreOrder(p->lChild);//遍历左子树PreOrder(p->rChild); //遍历右子树}if (p == NULL){cout << "*";//输出空的节点,更清楚的理解PreOrder的调用过程}
}
//中序遍历
void InOrder(Node* p)
{if (p != NULL){InOrder(p->lChild); //遍历左子树cout << p->data; //访问树根InOrder(p->rChild);//遍历右子树}if (p == NULL){cout << "*";//输出空的节点,更清楚的理解PreOrder的调用过程}
}
//后序遍历
void PostOrder(Node* p)
{if (p != NULL){PostOrder(p->lChild);//遍历左子树PostOrder(p->rChild); //遍历右子树cout << p->data; //访问树根}if (p == NULL){cout << "*";//输出空的节点,更清楚的理解PreOrder的调用过程}
}
//主函数
int main()
{BinTree K, E, B, C, A;Create(K, 'K', NULL, NULL);//创建结点K的子树Create(E, 'E', NULL, K.root);//创建结点E的子树Create(B, 'B', NULL, E.root);//创建结点B的子树Create(C, 'C', NULL, NULL);//创建结点C的子树Create(A, 'A', B.root, C.root);//创建结点A的子树cout << "前序遍历为 "; PreOrder(A.root); cout << endl;cout << "中序遍历为 "; InOrder(A.root); cout << endl;cout << "后序遍历为 "; PostOrder(A.root); cout << endl;return 0;
}
程序运行的结果如图16所示:
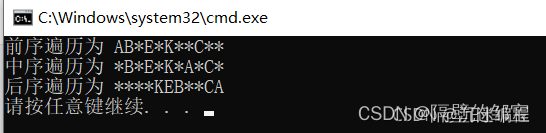
【定理1】任意n(n>0)个不同结点的二叉树,都可由其前序遍历序列和中序遍历序列唯一确定。
【例4】画出前序遍历ABEKC,中序遍历BEKAC所确定的二叉树。
(1)由前序遍历ABEKC,A为根结点;由中序遍历BEKAC,BEK为左子树,C为右子树;其对应的二叉树如图17所示。
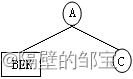
(2)对于左子树,由前序遍历BEK,B为根结点;由中序遍历BEK,EK为右子树,其对应的二叉树如图18所示。
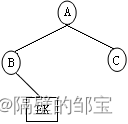
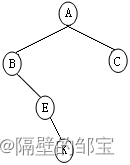
(3)对于右子树,由前序遍历EK,E为根结点;由中序遍历EK,K为右子树,其对应的二叉树如图19所示。
五、常用二叉树
5.1排序二叉树
先给出排序二叉树的定义。
设二叉树的所有结点值互异,排序二叉树或者是一棵空树,或者是满足以下条件的树:
(1)若左子树不空,则左子树上所有结点的值均小于根结点的值;(左小于根)
(2)若右子树不空,则右子树上所有结点的值均大于根结点的值;(右大于根)
(3)左、右子树也分别是排序二叉树。(递归定义)
排序二叉树定义是由递归方式给出的,据此定义,可给出排序二叉树的创建方法:
首次输入的数据作为此二叉树的根,其后输入的数据与根进行比较,小于树根的放置到左子树,大于树根的放置到右子树。
【例5】依次输入数据32,25,16,35,27,创建一棵排序二叉树。
排序二叉树的创建过程如图20所示:
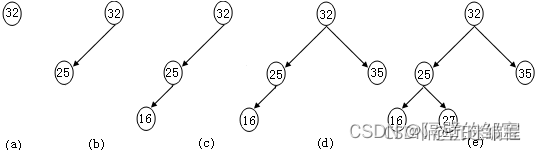
创建排序二叉树的程序如下:
#include <bits/stdc++.h>
using namespace std;
//二叉树结点定义
struct Node
{ int data;//数据域Node *lChild,*rChild;//指针域
};
//二叉树定义
struct BinTree
{ Node *root;
};
//创建空二叉树
void Create(BinTree &T)
{ T.root=NULL;
}//判空
int IsEmpty(BinTree T)
{ if(T.root==NULL) return 1;else return 0;
}
//创建排序二叉树
void Create(BinTree &T,int x)
{ Node *NewNode,*p;NewNode=new Node; //新结点申请内存NewNode->data=x;//新结点数据域赋值NewNode->lChild=NULL;//新结点左指针域赋值NewNode->rChild=NULL;//新结点右指针域赋值int flag=0;//新结点入树标识,flag=0表示未入树if(IsEmpty(T))//如果二叉树为空{T.root=NewNode;}else//如果二叉树非空{ p=T.root;//探测指针指向根结点while(!flag)//当新结点未入树时//理解江老师说的兑奖劵问题{ if(x<p->data)//如果新结点的值小于双亲结点的值{ //进入左子树if(p->lChild==NULL)//如果左子树为空{ p->lChild=NewNode;//新结点成为左子树flag=1;//新结点入树}else//如果左子树非空{p=p->lChild;//探测指针向左下移}}else//如果新结点的值大于双亲结点的值{ //进入右子树if(p->rChild==NULL)//如果右子树为空{ p->rChild=NewNode;//新结点成为右子树flag=1;//新结点入树}else{p=p->rChild;//探测指针向右下移}}}}
}
//前序遍历
void PreOrder(Node *p)
{ if(p!=NULL){ cout<<p->data<<" ";//访问树根PreOrder(p->lChild);//遍历左子树PreOrder(p->rChild);//遍历右子树}
}
//中序遍历
void InOrder(Node *p)
{ if(p!=NULL){ InOrder(p->lChild);//遍历左子树cout<<p->data<<" ";//访问树根InOrder(p->rChild);//遍历右子树}
}
//主函数
int main()
{ BinTree T;//定义二叉树Create(T);//创建空二叉树char c;int x;printf("输入二叉树结点值(用空格隔开,回车结束)\n");while(scanf("%d%c",&x,&c))//while键盘输入的第一种用法{Create (T,x);//创建排序二叉树if(c=='\n') break;}cout<<"前序遍历为 "; PreOrder(T.root); cout<<endl;cout<<"中序遍历为 "; InOrder(T.root); cout<<endl;return 0;
}
程序运行的结果如图21所示:
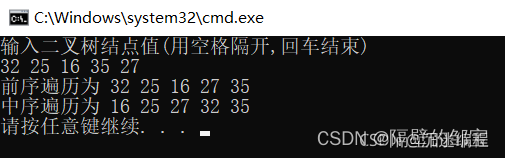
排序二叉树的优点是,建树方便,中序遍历为升序序列。
5.2哈夫曼树
先介绍几个概念 。
路径长度(Path Length): 路径上的分支(边)数目。
树的路径长度(Tree Path Length): 根结点到每个叶子结点的路径长度之和。
树的带权(叶子结点的权值)路径长度(Weighted Path Length): 其中wi是第i个叶子结点的权值,li为从根结点到第i个叶子结点的路径长度,n为叶子结点的总数。
最优二叉树: WPL最小的二叉树,最优二叉树也称哈夫曼树(Huffman Tree)。
【例6】图27给出了三棵二叉树,分别计算它们的带权路径长度(即 W P L WPL WPL )。
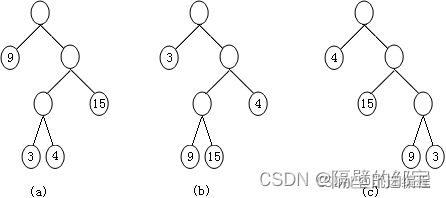
图27 二叉树的带权路径长度
解:
(a) W P L = 9 × 1 + 15 × 2 + 3 × 3 + 4 × 3 = 60 WPL=9×1+15×2+3×3+4×3=60 WPL=9×1+15×2+3×3+4×3=60
(b) W P L = 3 × 1 + 4 × 2 + 9 × 3 + 15 × 3 = 83 WPL=3×1+4×2+9×3+15×3=83 WPL=3×1+4×2+9×3+15×3=83
(c) W P L = 4 × 1 + 15 × 2 + 9 × 3 + 3 × 3 = 70 WPL=4×1+15×2+9×3+3×3=70 WPL=4×1+15×2+9×3+3×3=70
哈夫曼给出了一个创建最优二叉树的方法。下面,我们用一个实例来介绍这一方法。
【例7】设集合{12,3,10,5,2}为叶结点的权值,试创建哈夫曼树。
创建哈夫曼树的过程,可以由以下步骤和示意图来说明。
(1)将权值按升序排序,构建单结点的二叉树集T,T如图28所示。
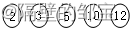
图28
(2)从T中选取前两棵的二叉树,分别作为左、右子树,构造一棵新二叉树(注意,排序在前的作左子树),对T中权值再按升序排序(注意,如果出现权值相等的情况,则原树排前,新树排后),T如图29所示。
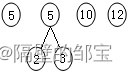
图29
(3)反复重复第(2)步的操作,T如图30 — 图32所示。
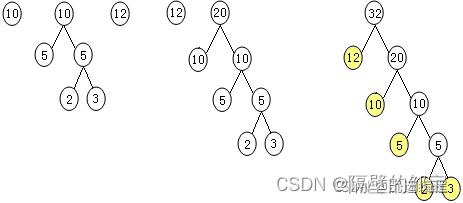
图30 创建过程3 图31 创建过程4 图32 创建过程5
必须指出,哈夫曼树的形状不唯一。但如果严格按上述规定来创建,哈夫曼树还是唯一
的,编程创建哈夫曼树将严格按上述规定进行。
性质1: 哈夫曼树不存在度为1的结点。
性质2: 设哈夫曼树的叶子结点数为 n 0 n_0 n0,则哈夫曼树的结点数 n = 2 × n 0 − 1 n=2×n_0-1 n=2×n0−1。
性质3: 哈夫曼树的带权路径长度等于所有度为2的结点值之和。
相关文章:

树与图c++
1.树 前言 本文主要介绍的数据结构之树型结构的相关知识,树型数据结构是面试官面试的时候非常喜欢考的一种数据结构,树形结构的遍历也是大厂笔试非常喜欢设置的考点,这些内容都会在本篇文章中进行详细的介绍,并且还会介绍一些常…...
中小企业常用的 IT 项目管理软件有哪些?
越热门,越贵的IT项目管理软件越好用吗?对于预算有限的中小型企业来说,如何选择一款适合自己的项目管理工具着实是个头疼的问题。 首先适用于中小型企业使用的 IT 项目管理软件需要具备哪些特点呢? 1、简单易用:中小企…...

汇编原理计算方法:物理地址=段地址*16+偏移地址
文章目录 计算方法计算错误分析 计算方法 根据进制的不同选择不同的计算方法 注意:物理地址、段地址和偏移地址的进制统一,要么都是二进制,要么都是十六进制,一般而言多是十六进制 若是二进制表达,则将段地址左移四…...
jdk-8u371-linux-x64.tar.gz jdk-8u371-windows-x64.exe 【jdk-8u371】 全平台下载
jdk-8u371 全平台下载 jdk-8u371-windows-x64.exejdk-8u371-linux-x64.rpmjdk-8u371-linux-x64.tar.gzjdk-8u371-macosx-x64.dmgjdk-8u371-linux-aarch64.tar.gz 下载地址 迅雷云盘 链接:https://pan.xunlei.com/s/VNdLL3FtCnh45nIBHulh_MDjA1?pwdw4s6 百度…...
数据结构体--5.0图
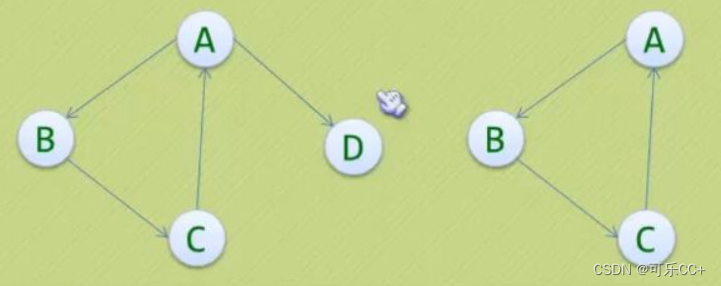
目录 一、定义 二、图的顶点与边之间的关系 三、图的顶点与边之间的关系 四、连通图 五、连通图的生成树定义 一、定义 图(Graph)是由顶点的又穷非空集合合顶点之间边的集合组成,通常表示为:G(V,E&…...

深入剖析 Golang 程序启动原理 - 从 ELF 入口点到GMP初始化到执行 main!
大家好,我是飞哥! 在过去的开发工作中,大家都是通过创建进程或者线程来工作的。Linux进程是如何创建出来的? 、聊聊Linux中线程和进程的联系与区别! 和你的新进程是如何被内核调度执行到的? 这几篇文章就是…...
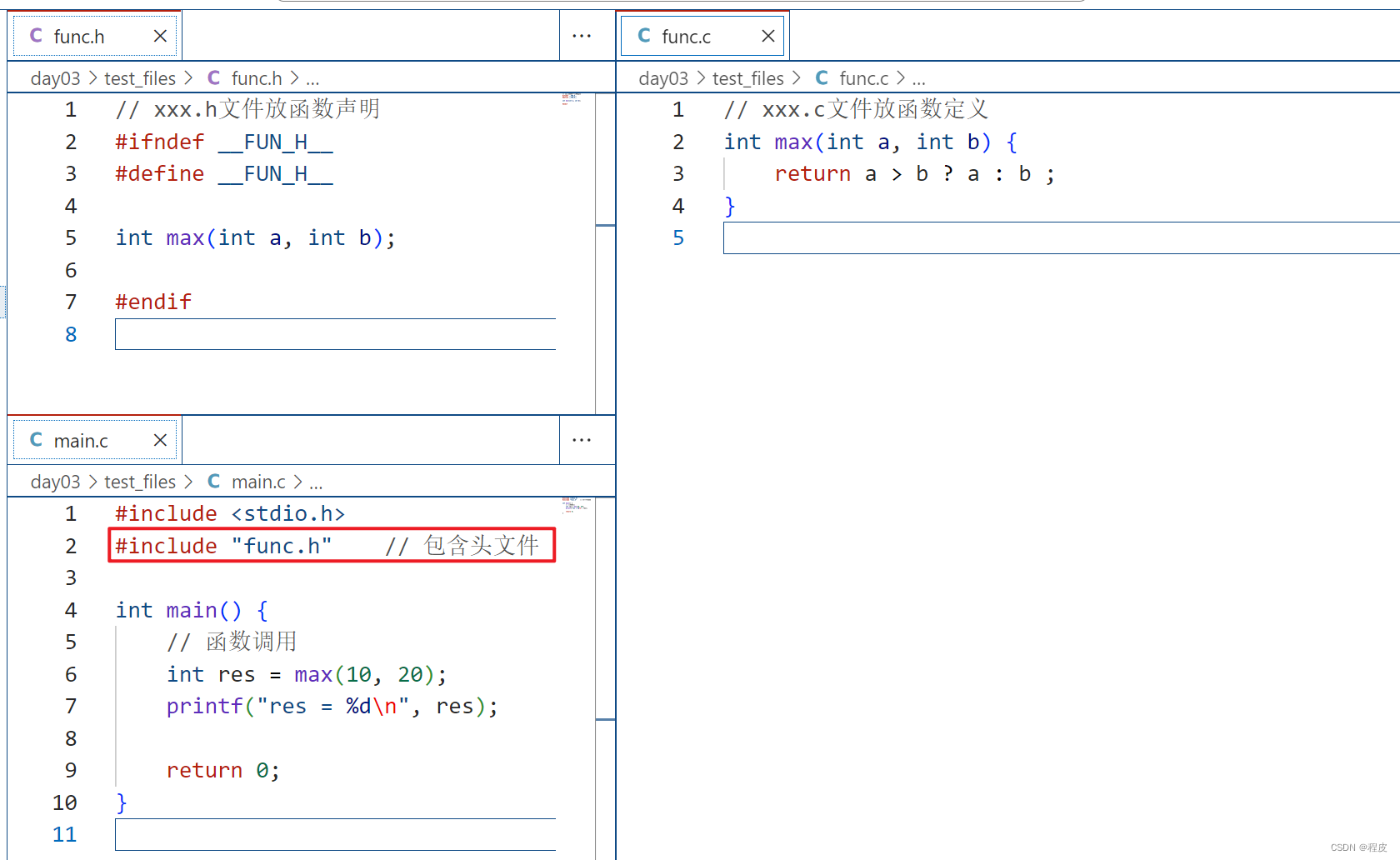
C语言——多文件编程
多文件编程 把函数声明放在头文件xxx.h中,在主函数中包含相应头文件在头文件对应的xxx.c中实现xxx.h声明的函数 防止头文件重复包含 当一个项目比较大时,往往都是分文件,这时候有可能不小心把同一个头文件 include 多次,或者头…...

Git学习part1
02.尚硅谷_Git&GitHub_为什么要使用版本控制_哔哩哔哩_bilibili 1.Git必要性 记录代码开发的历史状态 ,允许很多人同时修改文件(分布式)且不会丢失记录 2.版本控制工具应该具备的功能 1)协同修改 多人并行不悖的修改服务器端…...

2309C++均为某个类型
#include <常用> 构 A{空 f(){打印("啊");} }; 元<类 T>构 是点啊:假型{}; 元<>构 是点啊<A>:真型{}; 元<类 T>概念 是呀是点啊<T>::值;元<是呀...T>空 f(T&...t){(t.f(),...); }//均为元<类...T>要求 均为值&l…...

2023年打脸面试官之TCP--瞬间就懂
1.TCP 三次握手之为什么要三次呢?事不过三? 过程如下图: 先来解释下上述的各个标志的含义 序列号seq:占4个字节,用来标记数据段的顺序,TCP把连接中发送的所有数据字节都编上一个序号,第一个字节…...

设计模式-单例模式Singleton
单例模式 单例模式 (Singleton) (重点)1) 为什么要使用单例2) 如何实现一个单例2.a) 饿汉式2.b) 懒汉式2.c) 双重检查锁2.d) 静态内部类2.e) 枚举类2.f) 反射入侵2.g) 序列化与反序列化安全 3) 单例存在的问题3.a) 无法支持面向对象编程 单例模式 (Singleton) (重点) 一个类只…...

PPPoE连接无法建立的排查和修复
嗨,亲爱的读者朋友们!你是否曾经遇到过PPPoE连接无法建立的问题?今天我将为你详细解析排查和修复这个问题的步骤。 检查物理连接 首先,我们需要确保物理连接没有问题。请按照以下步骤进行检查: - 检查网线是否插好&…...

QT 发布软件基本操作
一、配置环境变量 找到Qt安装时的bin目录的路径:D:\Qt\Qt5.14.2\5.14.2\mingw73_64\bin,将目录拷贝至下述环境变量中。 打开计算机的高级系统设置 选中环境变量-->系统变量-->Path 点击编辑-->新建-->粘贴 二、生成发布软件的可执行程序 …...
CTFhub-SSRF-内网访问
CTFHub 环境实例 | 提示信息 http://challenge-8bf41c5c86a8c5f4.sandbox.ctfhub.com:10800/?url_ 根据提示,在url 后门添加 127.0.0.1/flag.php http://challenge-8bf41c5c86a8c5f4.sandbox.ctfhub.com:10800/?url127.0.0.1/flag.php ctfhub{a6bb51530c8f6be0…...

Cenos7安装小火车程序动画
运维Shell脚本小试牛刀(一) 运维Shell脚本小试牛刀(二) 运维Shell脚本小试牛刀(三)::$(cd $(dirname $0); pwd)命令详解 运维Shell脚本小试牛刀(四): 多层嵌套if...elif...elif....else fi_蜗牛杨哥的博客-CSDN博客 Cenos7安装小火车程序动画 一:替换…...

Node 执行命令时传参 process.argv
process 对象是一个全局变量,提供当前 Node.js 进程的有关信息,以及控制当前 Node.js 进程。 因为是全局变量,所以无需使用 require()。 process.argv 属性返回一个数组,这个数组包含了启动Node.js进程时的命令行参数,…...

【Vue】快速上手--Vue 3.0
什么是 Vue? Vue (发音为 /vjuː/,类似 view) 是一款用于构建用户界面的 JavaScript 框架。它基于标准 HTML、CSS 和 JavaScript 构建,并提供了一套声明式的、组件化的编程模型,帮助你高效地开发用户界面。无论是简单还是复杂的…...
PyTorch深度学习遥感影像地物分类与目标检测、分割及遥感影像问题深度学习优化实践技术应用
我国高分辨率对地观测系统重大专项已全面启动,高空间、高光谱、高时间分辨率和宽地面覆盖于一体的全球天空地一体化立体对地观测网逐步形成,将成为保障国家安全的基础性和战略性资源。未来10年全球每天获取的观测数据将超过10PB,遥感大数据时…...
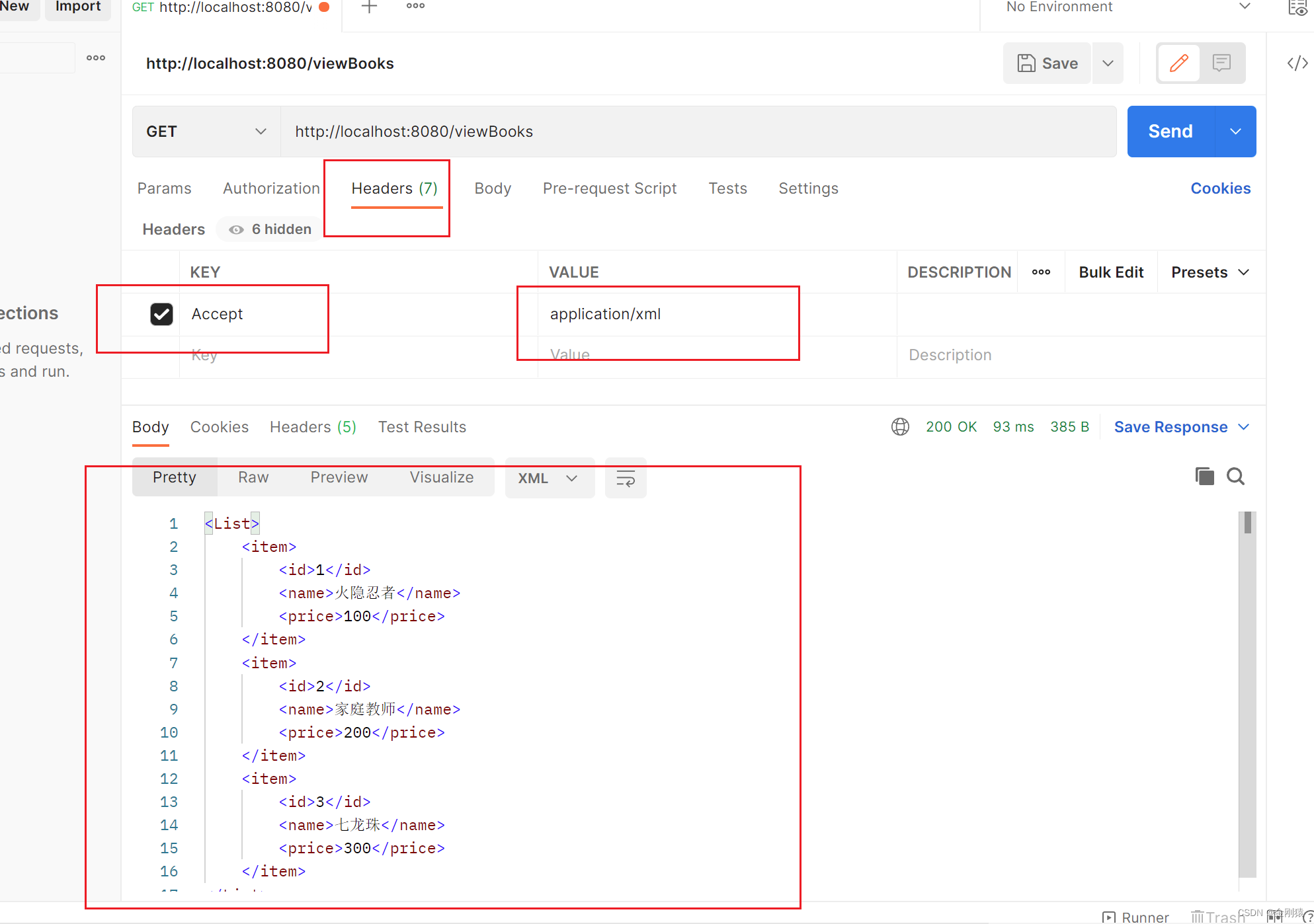
04、添加 com.fasterxml.jackson.dataformat -- jackson-dataformat-xml 依赖报错
Correct the classpath of your application so that it contains a single, compatible version of com.fasterxml.jackson.dataformat.xml.XmlMapper 解决: 改用其他版本,我没写版本号,springboot自己默认的是 2.11.4 版本 成功启动项目…...
禅道项目管理系统 - 操作使用 (2023版)
1. 部门-用户-权限 新增部门 新增用户 设置权限 2. 项目集创建 项目集 - 添加项目集 3. 产品线创建 产品 - 产品线 4. 产品创建 产品 - 产品列表 - 添加产品 5. 产品计划创建 产品 - xx产品 - 计划 - 创建计划 我这里创建3个计划 (一期, 二期, 三期) 6. 研发需求 - 创建模块…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
