大数据课程K16——Spark的梯度下降法
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州
▲ 本章节目的
⚪ 了解Spark的梯度下降法;
⚪ 了解Spark的梯度下降法家族(BGD,SGD,MBGD);
⚪ 掌握Spark的MLlib实现SGD;
一、梯度下降法概念
1. 概述
求解机器学习算法的模型参数,即无约束优化问题时,梯度下降法是最常采用的方法之一,另一种常用的方法是最小二乘法。这里对梯度下降法做简要介绍。
最小二乘法法适用于模型方程存在解析解的情况。如果说一个函数不存在解析解,是不能用最小二乘法的,此时,只能通过数值解(迭代式的)去逼近真实解。

上面的方程就不存在解析解,每个系数无法用变量表达式表达。
梯度下降法要比最小二乘法的适用性更强。
2. 什么是梯度
在微积分里面,对多元函数的参数求∂偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。
比如函数f(x,y), 分别对x,y求偏导数,求得的梯度向量就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。
![]()
![]()
对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)T.或者▽f(x0,y0),如果是3个参数的向量梯度,就是(∂f/∂x, ∂f/∂y,∂f/∂z)T,以此类推。
3. 这个梯度向量求出来有什么意义
他的意义从几何意义上讲,就是函数变化最快的地方。
具体来说,对于函数f(x,y),在点(x0,y0),沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。
反过来说,沿着梯度向量相反的方向,也就是 -(∂f/∂x0, ∂f/∂y0)T的方向,梯度减少最快,也就是更加容易找到函数的最小值。
二、梯度下降法与梯度上升法
在机器学习算法中,在求最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。
反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。
三、梯度下降法的直观解释
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步向谷底走下去。
从上面的解释可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
四、梯度下降法的相关概念
1. 步长:步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。用上面下山的例子,步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
一般步长的选择:0.1~0.05。步长过小,迭代次数可能过多,收敛速度慢。步长过大,可能会错过最优解,围绕最优解震荡而不收敛。
2. 特征:指的是样本中输入部分,比如样本(x0,y0),(x1,y1),则样本特征为x,样本输出为y。
3. 假设函数:在监督学习中,为了拟合输入样本,而使用的假设函数,比如一个线性函数:
![]()
4. 损失函数:为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方:
![]()
为了后续的求导运算方便,一般会乘以1/2
![]()
五、梯度下降法原理
1. 原理概述
1. 先决条件:确认优化模型的假设函数和损失函数;
2. 算法相关参数初始化:主要是初始化参数,算法终止距离以及步长。在没有任何先验知识的时候,可以将所有的参数初始化为0,将步长初始化为1.在调优时再优化;
2. 算法过程
1. 随机选择一个θ(θ1,θ2,……)的初始位置,
2. 用步长乘以损失函数的梯度,得到当前位置下降的距离,并更新下降后的θ
3. 多次迭代第二步,直至收敛于损失函数的极值
4. 得到极值点对应的θ解
![]()
3. 损失函数梯度的推导
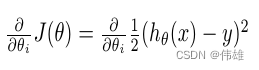
![]()
![]()
![]()
4. θi的更新表达式
![]()
上述θi的更新表达式是在只有一个样本的情况下,我们接下来推广到更一般的情况,比如有n个样本:
![]()
即当前点的梯度方向是由所有的样本决定的。
六、梯度下降法的算法参数
1. 算法的步长选择。在前面的算法描述中,提到取步长为1,但是实际上取值取决于数据样本,可以多取一些值,从大到小,分别运行算法,看看迭代效果,如果损失函数在变小,说明取值有效。
步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2. 算法参数的初始值选择。初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
3. 归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化。
七、梯度下降法家族(BGD,SGD,MBGD)
1. 批量梯度下降法(Batch Gradient Descent)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。
2. 随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法,和批量梯度下降法原理类似,区别在与求梯度时没有用所有的n个样本的数据,而是仅仅选取一个样本j来求梯度。
3. BGD和SGD对比
批量梯度下降法和随机梯度下降法是两个极端,一个采用所有数据来梯度下降,一个用一个样本来梯度下降。自然各自的优缺点都非常突出。
1. 对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。
2. 对于准确度来说,随机梯度下降法由于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。
3. 对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。批量梯度下降法 > 随机梯度下降法。
批量梯度下降法由于采用所有样本计算,所以收敛速度很快,即迭代很少次数就能够收敛到局部或全局最优解。
随机梯度是每次选取一个样本计算,所以收敛速度相比于批量来说就慢很多。
举个例子1:比如批量法10次迭代后收敛,随机法则可能需要100次迭代。
但在海量数据下,使用批量法就不适合了。
举个例子2:因为数据量巨大,批量法可能迭代1次就需要20分钟,而随机法迭代一次只需要1ms
所以总的耗时:批量法=10*20*60*1000ms 随机法=100*1ms。
4. MBGD小批量梯度下降法
结合了以上两种算法,应用没有随机梯度用的多。
对于迭代类型的算法,除了梯度下降法以外,还有牛顿法。
八、案例——MLlib实现SGD
1. 说明
首先需要数据准备工作。MLlib中,线性回归的基本数据是严格按照数据格式进行设置。
数据如下:
1,0 1
2,0 2
3,0 3
5,1 4
7,6 1
9,4 5
6,3 3
第一列是因变量,第二列和第三列是自变量
其次是对既定的MLlib回归算法中数据格式的要求,我们可以从回归算法的源码来分析,源码代码段如下:
def train(
input: RDD[LabeledPoint],
numIterations: Int,
stepSize: Double): LinearRegressionModel = {
train(input, numIterations, stepSize, 1.0)
}
从上面代码段可以看到,整理的训练数据集需要输入一个LabeledPoint格式的数据,因此在读取来自数据集中的数据时,需要将其转化为既定的格式。
从中可以看到,程序首先对读取的数据集进行分片处理,根据逗号将其分解为因变量与自变量,即线性回归中的y和x值。其后将其转换为LabeledPoint格式的数据,这里part(0)和part(1)分别代表数据分开的y和x值,并根据需要将x值转化成一个向量数组。
其次是训练模型的数据要求。numIterations是整体模型的迭代次数,理论上迭代的次数越多则模型的拟合程度越高,但是随之而来的是迭代需要的时间越长。而stepSize是随机梯度下降算法中的步进系数,代表每次迭代过程中模型的整体修正程度。
2. 代码示例
代码示例:
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LabeledPoint,LinearRegressionWithSGD}
import org.apache.spark.{SparkConf,SparkContext}
object Demo13{
val conf=new SparkConf().setMaster("local").setAppName("LinearRegression")
val sc=new SparkContext(conf)
def main(args:Array[String]):Unit={
val data=sc.textFile("d://testSGD.txt")
//转换成SGD要求的格式
val parsedData=data.map{line=>
val parts=line.split(",")
LabeledPoint(parts(0).toDouble,Vectors.dense(parts(1).split("").map(_.toDouble)))
}.cache()
//建立模型
val model=LinearRegressionWithSGD.train(parsedData,100,0.1)
//根据测试集检验模型
val prediction=model.predict(parsedData.map((_.features)))
prediction.foreach(println)//查看检验的结果
println("预测数据:x1=0,x2=1时y的取值"+model.predict(Vectors.dense(0,1)))
}
}
打印的结果:
1.0042991995986885
2.008598399197377
3.012897598796066
5.012535240851979
6.976329854342036
9.00284976782234
5.99891292616774
测数据:x1=0,x2=1时 y的取值1.0042991995986885。
相关文章:
大数据课程K16——Spark的梯度下降法
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解Spark的梯度下降法; ⚪ 了解Spark的梯度下降法家族(BGD,SGD,MBGD); ⚪ 掌握Spark的MLlib实现…...
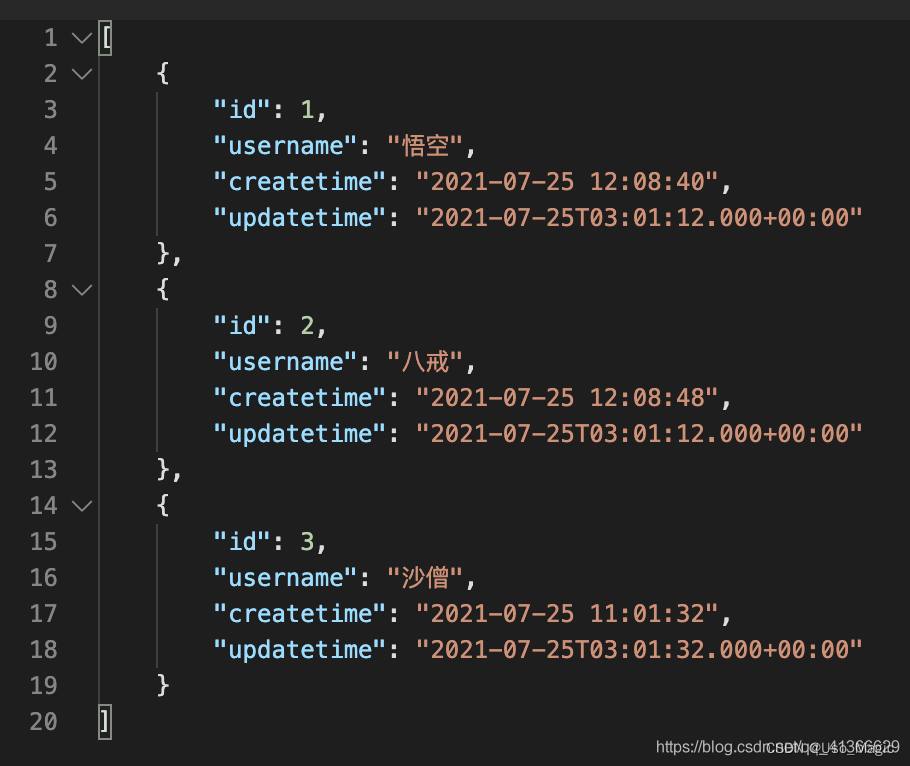
springboot:时间格式化的5种方法(解决后端传给前端的时间格式转换问题)推荐使用第4和第5种!
本文转载自:springboot:时间格式化的5种方法(解决后端传给前端的时间显示不一致)_为什么前端格式化日期了后端还要格式化_洛泞的博客-CSDN博客 时间问题演示 为了方便演示,我写了一个简单 Spring Boot 项目ÿ…...
六、vim编辑器的使用
1、编辑器 (1)编辑器就是一款软件。 (2)作用就是用来编辑文件,譬如编辑文字、编写代码。 (3)Windows中常用的编辑器,有自带的有记事本(notepad),比较好用的notepad、VSCode等。 (4)Linux中常用的编辑器,自带的最古老的vi&…...

【易售小程序项目】项目介绍与系列文章集合
项目介绍 易售二手小程序主要用于校园中二手商品的交易,该系列文章会记录这个小程序前端的整个开发过程并提供详细代码,后台主要基于若依管理系统搭建,文章中也会提及后端关键部分的实现及代码。希望该系列文章可以帮助小白了解项目的开发流…...

游戏服务器成DDoS最大攻击重灾区
游戏产业的迅猛发展也让游戏产业成为被黑客攻击的重灾区。什么原因让游戏行业成为DDoS的攻击重点。总结有如下原因和主要手段: 1.游戏行业的攻击成本较低,攻防成本1:N。随着DDoS攻击的打法越来越复杂,攻击点更是越来越多ÿ…...

[SpringBoot3]博客管理系统(源码放评论区了)
八、博客管理系统 创建新的SpringBoot项目,综合运用以上知识点,做一个文章管理的后台应用。依赖: Spring WebLombokThymeleafMyBatis FrameworkMySQL DriverBean Validationhutool 需求:文章管理工作,发布新文章&…...
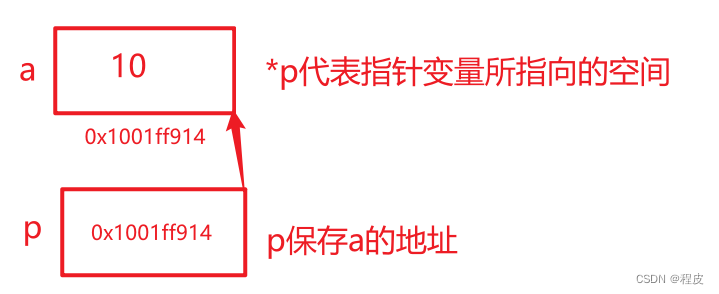
C语言——指针基本语法
概述 内存地址 在计算机内存中,每个存储单元都有一个唯一的地址(内存编号)。 通俗理解,内存就是房间,地址就是门牌号 指针和指针变量 指针(Pointer)是一种特殊的变量类型,它用于存储内存地址。 指针的实…...

elementui table 在浏览器分辨率变化的时候界面异常
异常点: 界面显示不完整,表格卡顿,界面已经刷新完成,但是表格的宽度还在一点一点变化,甚至有无线延伸的情况 思路: 1. 使用doLayout 这里官方文档有说明, 所以我的想法是,监听浏览…...
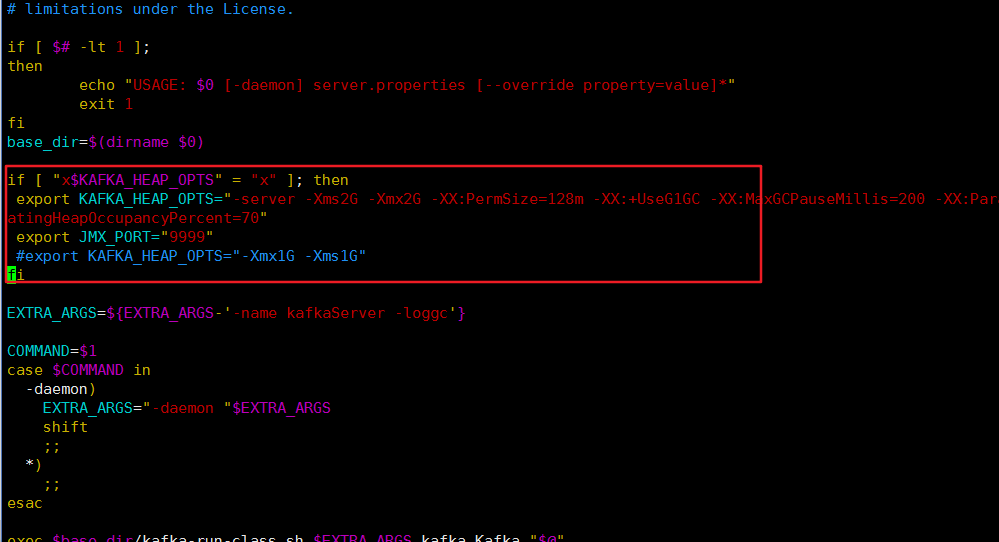
六、Kafka-Eagle监控
目录 6.1 MySQL 环境准备6.2 Kafka 环境准备6.3 Kafka-Eagle 安装 6.1 MySQL 环境准备 Kafka-Eagle 的安装依赖于 MySQL,MySQL 主要用来存储可视化展示的数据 6.2 Kafka 环境准备 修改/opt/module/kafka/bin/kafka-server-start.sh 命令 vim bin/kafka-server-sta…...

DBeaver 23.1.5 发布
导读DBeaver 是一个免费开源的通用数据库工具,适用于开发人员和数据库管理员。DBeaver 23.1.5 现已发布,更新内容如下. Data editor 重新设计了词典查看器面板 UI 空间数据类型:曲线几何线性化已修复 数据保存时结果选项卡关闭的问题已解决…...

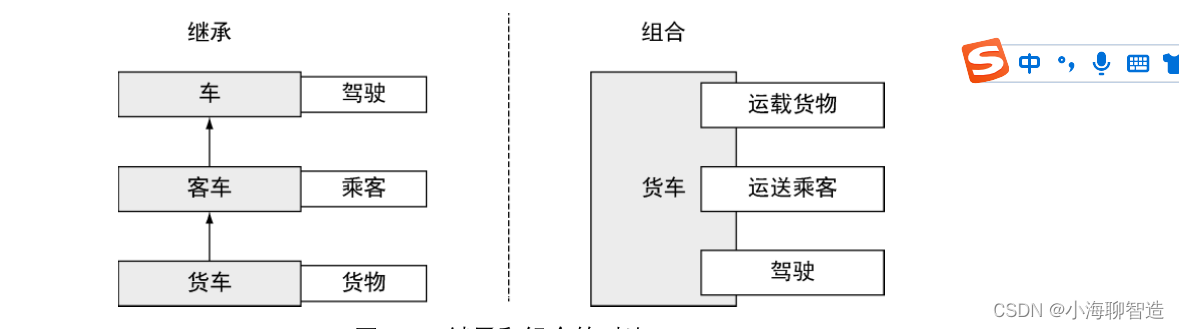
三种垃圾收集算法,优缺点分析,设计垃圾收集
文章目录 垃圾收集算法标记-清除(基础收集算法)标记-复制(新生代)标记-整理(老年代) 垃圾收集算法 标记-清除(基础收集算法) 首先标记出所有需要回收的对象,在标记完成后…...

【链表OJ 10】环形链表Ⅱ(求入环节点)
前言: 💥🎈个人主页:Dream_Chaser~ 🎈💥 ✨✨刷题专栏:http://t.csdn.cn/UlvTc ⛳⛳本篇内容:力扣上链表OJ题目 目录 leetcode142. 环形链表 II 1.问题描述 2.代码思路 3.问题分析 leetcode142. 环形链…...

RT-Thread在STM32硬件I2C的踩坑记录
RT-Thread在STM32硬件I2C的踩坑记录 0.前言一、软硬件I2C区别二、RT Thread中的I2C驱动三、尝试适配硬件I2C四、i2c-bit-ops操作函数替换五、Attention Please!六、总结 参考文章: 1.将硬件I2C巧妙地将“嫁接”到RTT原生的模拟I2C驱动框架 2.基于STM32F4平台的硬件I…...
小白学Go基础01-Go 语言的介绍
Go 语言对传统的面向对象开发进行了重新思考,并且提供了更高效的复用代码的手段。Go 语言还让用户能更高效地利用昂贵服务器上的所有核心,而且它编译大型项目的速度也很快。 用 Go 解决现代编程难题 Go 语言开发团队花了很长时间来解决当今软件开发人员…...

Spring工具类--Assert的使用
原文网址:Spring工具类--Assert的使用_IT利刃出鞘的博客-CSDN博客 简介 说明 本文介绍Spring的Assert工具类的用法。 Assert工具类的作用:判断某个字段,比如:断定它不是null,如果是null,则此工具类会报…...

无涯教程-Android - Absolute Layout函数
Absolute Layout 可让您指定其子级的确切位置(x/y坐标),绝对布局的灵活性较差且难以维护。 Absolute Layout - 属性 以下是AbsoluteLayout特有的重要属性- Sr.NoAttribute & 描述1 android:id 这是唯一标识布局的ID。 2 android:layout_x 这指定视图的x坐标…...

2018ECCV Can 3D Pose be Learned from2D Projections Alone?
摘要 在计算机视觉中,从单个图像的三维姿态估计是一个具有挑战性的任务。我们提出了一种弱监督的方法来估计3D姿态点,仅给出2D姿态地标。我们的方法不需要2D和3D点之间的对应关系来建立明确的3D先验。我们利用一个对抗性的框架,强加在3D结构…...

干旱演变研究:定义及研究方法
在水文系统中,每个组分之间互相关联,包气带水、地下水和河川径流相互响应,水文循环处于动态平衡的状态。 降水作为水文系统的输入量,对水文循环具有重要的影响。降水短缺通过水文循环导致水文系统不同组分(包气带、地下水和地表水)发生干旱,降水不足导致土壤含水量减少,…...
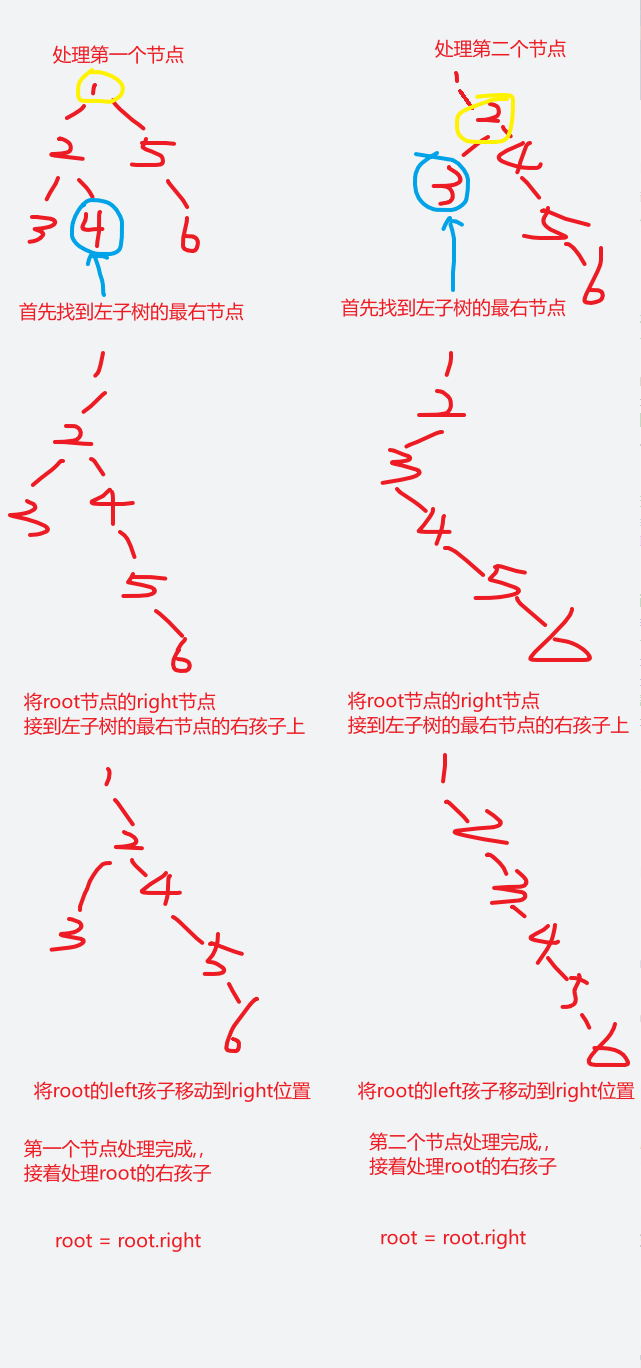
【LeetCode-中等题】114. 二叉树展开为链表
文章目录 题目方法一:前序遍历(构造集合) 集合(构造新树)方法二:原地构建方法三:前序遍历--迭代(构造集合) 集合(构造新树) 题目 方法一&#x…...

【题解】JZOJ6645 / 洛谷P4090 [USACO17DEC] Greedy Gift Takers P
洛谷 P4090 [USACO17DEC] Greedy Gift Takers P 题意 n n n 头牛排成一列,队头的奶牛 i i i 拿一个礼物并插到从后往前数 c i c_i ci 头牛的前面,重复无限次,问多少奶牛没有礼物。 题解 发现若一头牛无法获得礼物,那么它后…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
