手撕红黑树
学了很久编程了,红黑树在我们耳边早就如雷贯耳,都说他是数据结构中最难的几种结构了,但是,实际上学会了之后,你会发现他还是很简单的,个人认为他还没有AVL树的旋转难,好了,老规矩,来上代码:
#pragma once
#pragma once
#include <iostream>
#include <set>
#include <map>
#include <assert.h>
#include <math.h>
#include <vector>
using namespace std;
namespace cc
{enum colour{RED,BLACK};template<class K, class V>struct RBtreenode{colour _col;pair<K, V> _val;RBtreenode<K, V>* _left;RBtreenode<K, V>* _right;RBtreenode<K, V>* _parent;RBtreenode(const pair<K, V>& x):_val(x), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}};template<class K, class V>class RBtree{public:typedef RBtreenode<K, V> node;void reor(node* parent){node* sub = parent->_left;node* subr = sub->_right;if (_root == parent){_root = sub;sub->_parent = nullptr;sub->_right = parent;parent->_parent = sub;parent->_left = subr;if (subr)subr->_parent = parent;}else{node* pparent = parent->_parent;if (pparent->_left == parent)pparent->_left = sub;elsepparent->_right = sub;sub->_parent = pparent;sub->_right = parent;parent->_parent = sub;parent->_left = subr;if (subr)subr->_parent = parent;}}void reol(node* parent){node* sub = parent->_right;node* subl = sub->_left;if (_root == parent){_root = sub;sub->_parent = nullptr;sub->_left = parent;parent->_parent = sub;parent->_right = subl;if (subl)subl->_parent = parent;}else{node* pparent = parent->_parent;if (pparent->_left = parent)pparent->_left = sub;elsepparent->_right = sub;sub->_parent = pparent;sub->_left = parent;parent->_parent = sub;parent->_right = subl;if (subl)subl->_parent = parent;}}bool insert(const pair<K, V>& x){if (_root == nullptr){_root = new node(x);_root->_col = BLACK;return true;}node* parent = nullptr;node* cur = _root;while (cur){if (x.first < cur->_val.first){parent = cur;cur = cur->_left;}else if (x.first > cur->_val.first){parent = cur;cur = cur->_right;}elsereturn false;}cur = new node(x);if (parent->_val.first > x.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;node* grandfather = parent->_parent;while (parent && parent->_col == RED){if (grandfather->_left == parent){node* uncle = grandfather->_right;//情况一:只染色if (uncle && uncle->_col == RED){uncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;if (grandfather == _root){grandfather->_col = BLACK;break;}}//情况二+三:旋转+染色else if (uncle && uncle->_col == BLACK){if (parent->_left == cur){//单旋reor(grandfather);//染色grandfather->_col = RED;parent->_col = BLACK;}else{//双旋reol(parent);reor(grandfather);//染色cur->_col = BLACK;//爷爷节点变红grandfather->_col = RED;}break;}else if (uncle == nullptr){if (parent->_left == cur){reor(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{reol(parent);reor(grandfather);grandfather->_col = RED;cur->_col = BLACK;}break;}}else{node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){uncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;if (_root == grandfather){grandfather->_col = BLACK;break;}}else if (uncle && uncle->_col == BLACK){if (parent->_left == cur){reor(parent);reol(grandfather);grandfather->_col = RED;cur->_col = BLACK;}else{reol(grandfather);grandfather->_col = RED;parent->_col = BLACK;}break;}else if (uncle == nullptr){if (parent->_left = cur){reor(parent);reol(grandfather);cur->_col = BLACK;grandfather->_col = RED;}else{reol(grandfather);parent->_col = BLACK;grandfather->_col = RED;}break;}}cur = grandfather;parent = cur->_parent;grandfather = parent->_parent;}return true;}bool check(){return _check(_root);}void print(){prin(_root);}void prin(node* root,int num){if (root == nullptr)return;if (root->_col == BLACK)num++;if (root->_left == root->_right &&root->_left == nullptr)cout << num << endl;prin(root->_left,num);prin(root->_right,num);}bool _check(node* root){if (root == nullptr){if (root->_col != BLACK)exit(-1);return true;}if (root->_parent && root->_parent->_col == RED){cout << "异常退出" << endl;exit(-1);}int num = 0;prin(root, num);}private:node* _root = nullptr;};
}
其实和AVL树的代码差不多,唯一不同的是,我们没有平衡因子了,但是有颜色。
下面来说说红黑树的规则:
1.一个节点不是红色就是黑色
2.根节点必须是黑色
3.红色节点的两个孩子必须是黑色节点
4.每条路径的黑色节点个数相同
5.叶子结点(NIL节点)是黑色的
上面就是红黑树的规则,红黑树的代码就在上面,现在说一下红黑树的具体实现规则:
1.如果叔叔节点存在且叔叔节点为红色,那么,把父节点和叔叔节点染成黑色,组父节点染成红色,如果此时的祖父节点是根节点,那么,就在把祖父节点染成黑色。如果不是,就把新插入的节点更新成祖父节点,依次往上更新,直到父节点为空或是父节点的颜色为黑色就停止。
2.如果叔叔节点存在,且叔叔节点是黑色的,那么此时就要判断新插入的节点在父节点的左还右,如果父节点,祖父节点,新插入的节点成一条线,那么此时就是单旋,然后旋转完成之后把父节点染成黑色,祖父节点染成红色。
3.如果叔叔节点存在,且为黑色,新插入节点与父节点,祖父节点形成折线,那么此时应该是双旋,旋转完成之后,把新插入的节点染成黑色,祖父节点染成红色。
4.如果叔叔节点不存在,那就看是上面的额那种情况,是那种旋转,找到对应的旋转就好了。
以上就是实现红黑树代码的具体细节。
AVL树和红黑树的对比:
其实AVL树和红黑树两个各有各的好处,是的,个人认为两个各有各的好处,因为AVL对树高比较严格,所以导致旋转点额次数就多,所以就会有额外的消耗,但是红黑树就没有这么多的消耗了,因为红黑树的上面几个规则,导致红黑树最长路径不得超过对短路径的两倍,所以,红黑树也会旋转,但是插入同等节点的条件下,红黑树旋转点次数肯定比AVL树少,但是AVL树是严格的logn,而红黑树是不太严格的logn,所以我说是各有各的好。
以上就是红黑树的规则讲解以及代码实现。希望大家能够多多支持!!谢谢!
相关文章:

手撕红黑树
学了很久编程了,红黑树在我们耳边早就如雷贯耳,都说他是数据结构中最难的几种结构了,但是,实际上学会了之后,你会发现他还是很简单的,个人认为他还没有AVL树的旋转难,好了,老规矩&am…...
技术)
举例说明自然语言处理(NLP)技术
自然语言处理(NLP)技术是一种人工智能领域的技术,用于处理自然语言文本或语音信号。下面是一些自然语言处理技术的例子: 机器翻译:机器翻译是一种自然语言处理的技术,它可以将一种语言的文本翻译成另一种语…...

淘宝详情API接口在各种应用中的作用性
标题:淘宝详情API接口在各种应用中的作用性 一、引言 随着互联网的快速发展和电子商务的广泛应用,淘宝作为中国最大的C2C电商平台,其提供的API接口在各种应用中发挥着越来越重要的作用。本文将详细介绍淘宝详情API接口的背景、定义、类型&a…...

java用正则方法验证文件名是否合法
Java中用到文件操作时,经常要验证文件名是否合法. 用File类的createNewFile()方法的确很管用.但当要批量验证时,效率上就会有问题.正则匹配的开销比创建文件少了很多. 那么一个合法的文件(Win下)应该符合如下规则: 1.文件名不能为空,空在这里有两个意思: 文件名(包括扩展名…...
【learnopengl】Assimp构建与编译
文章目录 【learnopengl】Assimp构建与编译1 前言2 Assimp构建与编译2.1 下载源码2.2 CMake构建2.3 VS2022编译 3 在VS中配置Assimp库4 验证 【learnopengl】Assimp构建与编译 1 前言 最近在跟着LearnOpenGL这个网站学习OpenGL,这篇文章详细记录一下教程中关于Ass…...
小兔鲜商02
npm i vueuse/core -fvue插件使用: 许多公用的全局组件,,可以通过插件注册进去,就不用一个一个导入组件,, import XtxSkeleton from /components/library/xtx-skeletonexport default {install (app) {// …...

一键替换工程文件和场景中的UI对象字体
具体流程: 找到工程中使用到的所有字体找到工程和场景中包含Text的所有对象展示要替换的字体名字让用户选择通过用户选择的字体,展示响应的物体对象一键替换 通过AssetDatabase.FindAssets找到工程中包含的所有字体: private List<strin…...
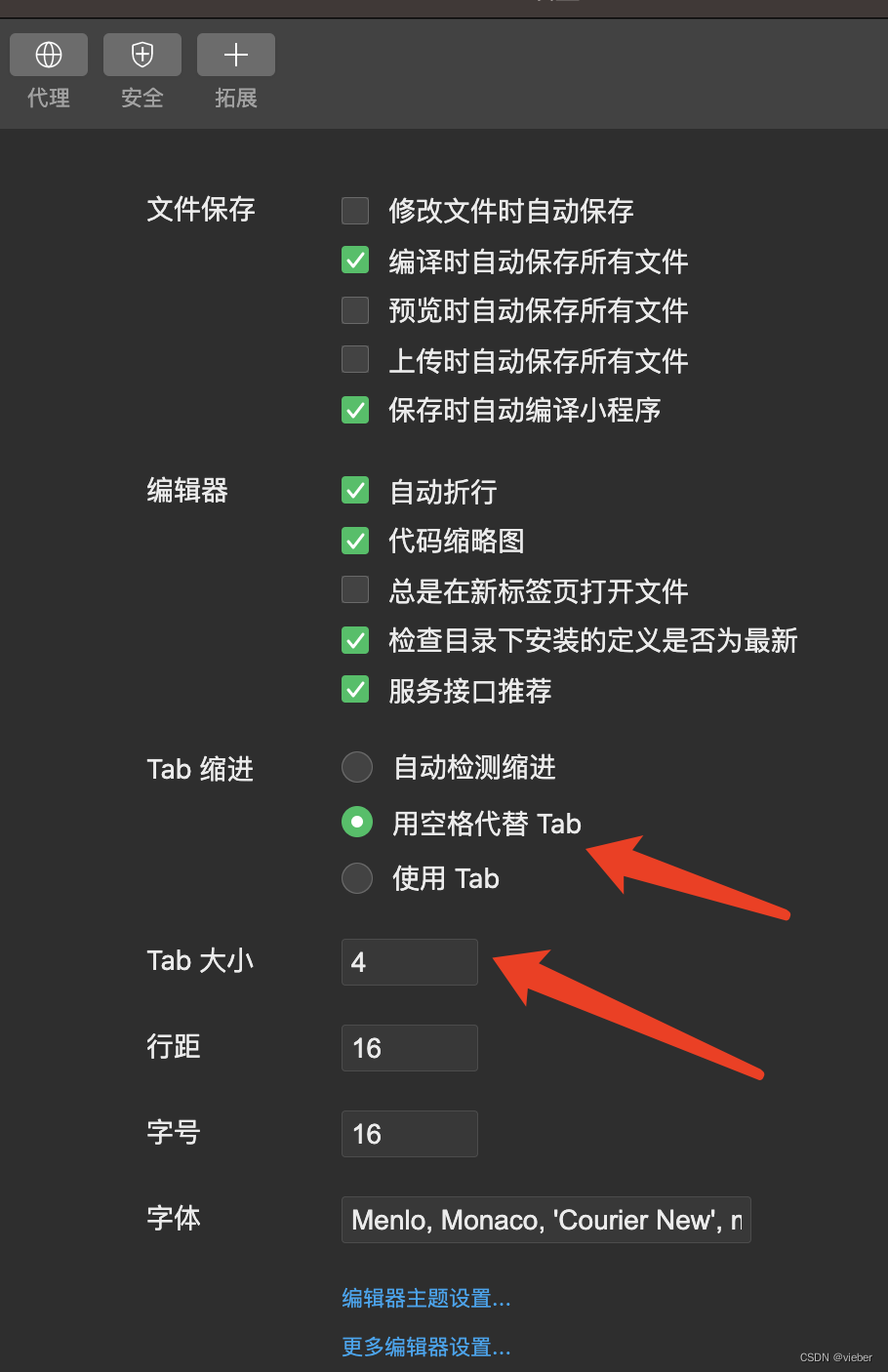
微信小程序编辑器代码格式缩进设置
第一步点击这个编辑器设置: 然后设置tab为空格,并且设置占几个空格,这里是4个空格。 这样就好了,文件保存就会自动设置好缩进格式了。...
Android Aidl跨进程通讯(二)--异常捕获处理
学更好的别人, 做更好的自己。 ——《微卡智享》 本文长度为1623字,预计阅读5分钟 前言 上一篇《Android Aidl跨进程通讯的简单使用》中介绍了跨进程的通讯处理,在进程间的数据通过Aidl实现了交互,项目中经常会遇到Bug,…...
)
Android中OkHttp源码阅读二(责任链模式)
博主前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住也分享一下给大家 👉点击跳转到教程 Android OkHttp源码阅读详解一 看OkHttp源码,发现OkHttp里面使用了责任链设计模式,所以才要学习…...

2023年03月 C/C++(六级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:波兰表达式 波兰表达式是一种把运算符前置的算术表达式,例如普通的表达式2 + 3的波兰表示法为+ 2 3。波兰表达式的优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2 + 3) * 4的波兰表示法为* + 2 3 4。本题求解…...
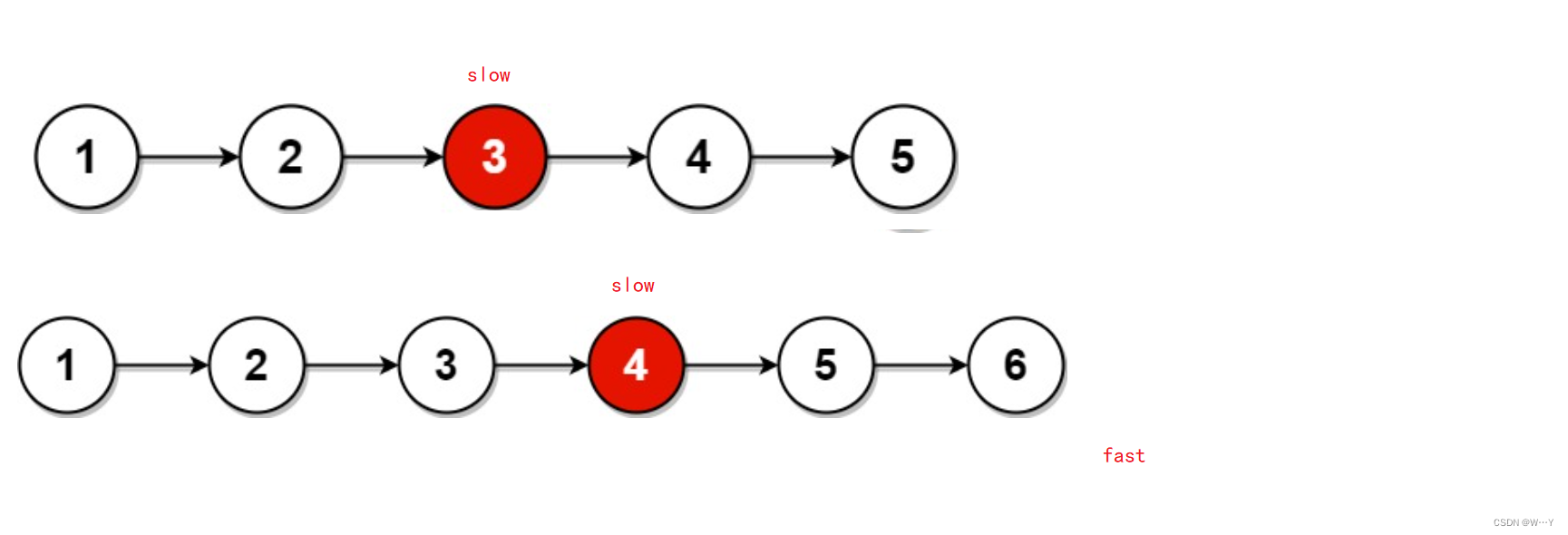
顺序表链表OJ题(1)——【LeetCode】
W...Y的主页 😊 代码仓库分享 💕 前言: 今天我们来回顾一下顺序表与链表,针对这一块我们也有许多OJ题目供大家参考。当我们学习完顺序表链表后避免不了一些习题的练习,这样才能巩固我们学习的内容。 话不多说…...

flex:1
问题1:“flex: 1” 与其他 “flex” 值有何区别? 答案: “flex: 1” 是 “flex” 属性的一种简写形式,它将 “flex-grow”、“flex-shrink” 和 “flex-basis” 设置为特定的值。与其他 “flex” 值相比,“flex: 1” …...

iOS练手项目知识点汇总
基础理解篇 Objective-C是一种面向对象的编程语言,它支持元编程。元编程是指编写程序来生成或操纵其他程序的技术。 Objective-C中,元编程可以使用Objective-C的动态特性来实现。例如可以使用Objective-C的运行时函数来动态地创建类、添加属性和方法等等…...

【Linux】Libevent相关小知识总结
Libevent是基于事件的,也就是说,相当于去注册一个事件,当这个事件发生的话,那么就会调用回调函数。...

【Spring Security】UserDetailsService 接口介绍
文章目录 UserDetailsService 介绍UserDetailsService 具体操作UserDetailsService 方法介绍 UserDetailsService 介绍 UserDetailsService 在 Spring Security 中主要承担查询系统内用户、验证密码、封装用户信息和角色权限。大白话就是你写一个实现类实现 UserDetailsServic…...
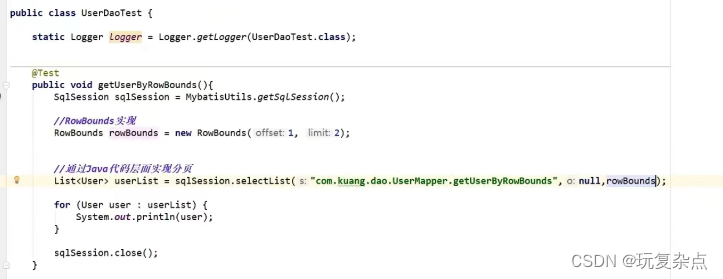
Mybatis学习|日志工厂、分页
1.日志工厂 如果一个数据库操作,出现了异常,我们需要排错。日志就是最好的助手! 曾经: sout、debug 现在:日志工厂! 我们主要掌握STDOUT_LOGGING 和LOG4j 在Mybatis中具体使用哪个一日志实现,在设置中设定! 在mybatis核心配置文件中&#…...
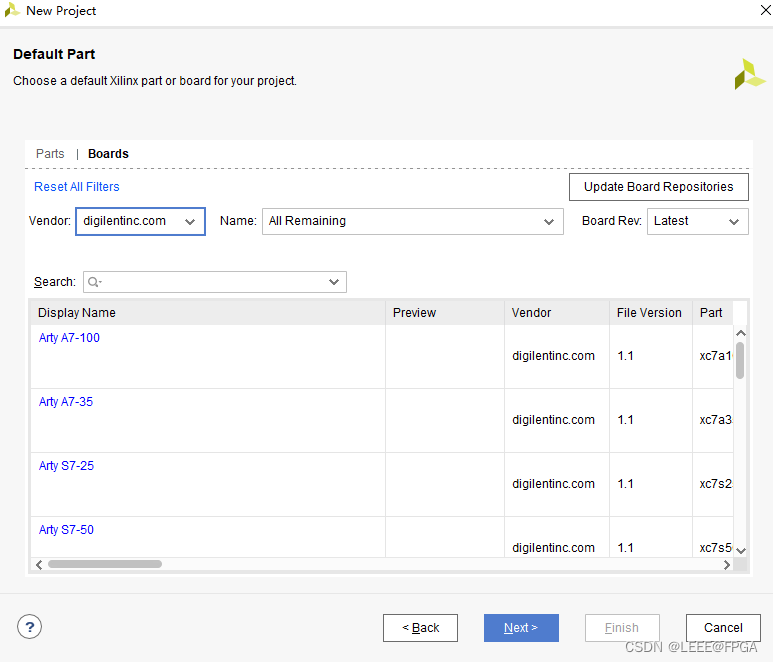
Vivado 添加FPGA开发板的Boards file的添加
1 digilent board file 下载地址 下载地址 : https://github.com/Digilent/vivado-boards 2 下载后 3 添加文件到 vivado 安装路径 把文件复制到 Vivado\2019.1\data\boards\board_files4 创建工程查看是否安装成功...

vmstat
vmstat VirtualMeomoryStatistics,虚拟内存统计,是Linux中监控内存的常用工具,可对操作系统的虚拟内存、进程、CPU等的整体情况进行监视。 [rootwenzi wenzi]# vmstat procs -----------memory---------- ---swap-- -----io---- -system--…...

LinuxShell变量
变量: 命名规则: 在Shell中,变量名可以由字母、数字或者下划线组成,并且只能以字母或者下划线开头。对于变量名的长度,Shell并没有做出明确的规定。因此,用户可以使用任意长度的字符串来作为变量名。但是…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
