2021江苏省赛热身赛 C Magic Rabbit(数形结合)
2021江苏省赛热身赛 C Magic Rabbit(数形结合)
Magic Rabbit
非常好且巧妙地一道题。
大意:给出三种溶液 , 三种溶液分别含有不同浓度的 x ,y 两种物质。
| 溶液 | x (mg/ml) | y (mg/ml) |
|---|---|---|
| 溶液1 | x1 | y1 |
| 溶液2 | x2 | y2 |
| 溶液3 | x3 | y3 |
给出 Q 组询问 , 每次给出一个新的溶液浓度(x4 , y4) , 问是否能用以上三种溶液混合出当前溶液。
思路:不妨设 溶液 1 , 2 , 3 分别取 a , b , c ml
显然可以得到式子
a x 1 + b x 2 + c x 3 a + b + c = x 4 \frac{ax_1+bx_2+cx_3}{a+b+c} = x_4 a+b+cax1+bx2+cx3=x4
a y 1 + b y 2 + c y 3 a + b + c = y 4 \frac{ay_1+by_2+cy_3}{a+b+c} = y_4 a+b+cay1+by2+cy3=y4
问题就变成了求这个方程组是否有解 , 显然是不好求的。
这时候我们转变思路 , 先求两种溶液的情况。
a x 1 + b x 2 a + b = x 4 \frac{ax_1+bx_2}{a+b} = x_4 a+bax1+bx2=x4
a y 1 + b y 2 a + b = y 4 \frac{ay_1+by_2}{a+b} = y_4 a+bay1+by2=y4
设
λ = a a + b \lambda = \frac{a}{a+b} λ=a+ba
λ x 1 + ( 1 − λ ) x 2 = x 4 \lambda x_1+(1-\lambda )x_2 = x_4 λx1+(1−λ)x2=x4
λ y 1 + ( 1 − λ ) y 2 = y 4 \lambda y_1+(1-\lambda )y_2 = y_4 λy1+(1−λ)y2=y4
转化成向量组的形式
[ x 2 y 2 ] + λ [ x 1 − x 2 y 1 − y 2 ] = [ x 4 y 4 ] ( 0 ≤ λ ≤ 1 ) \begin{bmatrix} x_2\\y_2 \end{bmatrix} +\lambda \begin{bmatrix} x_1-x_2\\y_1-y_2 \end{bmatrix}=\begin{bmatrix} x_4\\y_4 \end{bmatrix}(0\le \lambda\le 1) [x2y2]+λ[x1−x2y1−y2]=[x4y4](0≤λ≤1)
观察方程的左边 , 显然是一个直线的点向式的形式 , 这个式子表明 , 我们要求的解一定在(x1 , y1) (x2 , y2) 这两个点所形成的线段上(不考虑退化情况)。
那么当加入第三个点之后 , 显然解一定在三点所形成三角形内部(包含端点) , 注意退化情况。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;//--------------------------------------------------------------
const double eps = 1e-5;
const double pi = acos(-1);
inline double sqr(double x) {return x * x;} //平方
int sign(double x){if(fabs(x) < eps) return 0;if(x > 0) return 1;return -1;
}//符号
struct point{double x , y;point(){}point(double a , double b) : x(a) , y(b){}friend point operator + (const point &a , const point &b){return point(a.x + b.x , a.y + b.y);}friend point operator - (const point &a , const point &b){return point(a.x - b.x , a.y - b.y);}friend bool operator == (const point &a , const point &b){return !sign(a.x - b.x) && !sign(a.y - b.y);}friend point operator * (const point &a , const double &b){return point(a.x * b , a.y * b);}friend point operator * (const double &a , const point &b){return point(a * b.x , a * b.y);}friend point operator / (const point &a , const double &b){return point(a.x / b , a.y / b);}//向量模长 double norm(){ return sqrt(sqr(x) + sqr(y));}
}; double det(const point &a , const point &b){return a.x * b.y - a.y * b.x;
}//叉积 判断两点共线 double dot(const point &a , const point &b){return a.x * b.x + a.y * b.y;
}//点积double dist(const point &a , const point &b){return (a - b).norm();
}//两点距离point rotate_point(const point &a , const point &p , double A){double tx = p.x - a.x , ty = p.y - a.y;return point(a.x + tx * cos(A) - ty * sin(A) , a.y + tx * sin(A) + ty * cos(A));
}// p 点 绕 a 点逆时针旋转 A 弧度int toleft(const point &p , const point &a , const point &b) {return sign(det(b - a , p - a));// 1 左 0 上 -1 右
}//只适用凸多边形//判断点 p 是否在线段 st 上(包括端点)
bool point_on_segment(point p , point s , point t){return sign(det(p - s , t - s)) == 0 && sign(dot(p - s , p - t)) <= 0;
}//判断两线段是否相交 ab cd
bool segment_intersect(const point &a , const point &b , const point &c , const point &d){//先判断 三点共线 或 四点共线if(point_on_segment(a , c , d) || point_on_segment(b , c , d) || point_on_segment(c , a , b) || point_on_segment(d , a , b)) return 1;if(sign(toleft(a , c , d)) * sign(toleft(b , c , d)) < 0 && sign(toleft(c , a , b)) * sign(toleft(d , a , b)) < 0) return 1;return 0;
}//--------------------------------------------------------------point p[4] , now;
double x , y;
int n;
signed main(){IOSfor(int i = 1 ; i <= 3 ; i ++){cin >> x >> y;p[i] = point{x , y};}cin >> n;int tag = -1;if(p[1] == p[2] && p[2] == p[3]) tag = 0;else if(point_on_segment(p[1] , p[2] , p[3])) tag = 1;else if(point_on_segment(p[2] , p[1] , p[3])) tag = 2;else if(point_on_segment(p[3] , p[1] , p[2])) tag = 3;else tag = 4;for(int i = 1 ; i <= n ; i ++){cin >> x >> y;now = {x , y};if(tag == 0){if(now == p[1]) cout << "YES\n";else cout << "NO\n";}if(tag == 1){if(point_on_segment(now , p[2] , p[3])) cout << "YES\n";else cout << "NO\n";}if(tag == 2){if(point_on_segment(now , p[1] , p[3])) cout << "YES\n";else cout << "NO\n";}if(tag == 3){if(point_on_segment(now , p[2] , p[1])) cout << "YES\n";else cout << "NO\n";}if(tag == 4){bool f = 0;if(point_on_segment(now , p[2] , p[3]) || point_on_segment(now , p[1] , p[3]) || point_on_segment(now , p[2] , p[1])) f = 1;if(toleft(now , p[2] , p[3]) > 0 && toleft(now , p[3] , p[1]) > 0 && toleft(now , p[1] , p[2]) > 0) f = 1;if(toleft(now , p[2] , p[3]) < 0 && toleft(now , p[3] , p[1]) < 0 && toleft(now , p[1] , p[2]) < 0) f = 1;if(f) cout << "YES\n";else cout << "NO\n";}}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
)
2021江苏省赛热身赛 C Magic Rabbit(数形结合)
2021江苏省赛热身赛 C Magic Rabbit(数形结合) Magic Rabbit 非常好且巧妙地一道题。 大意:给出三种溶液 , 三种溶液分别含有不同浓度的 x ,y 两种物质。 溶液x (mg/ml)y (mg/ml)溶液1x1y1溶液2x2y2溶液3x3y3 给出 Q 组询问 ,…...
:AES代码实现解析)
AES加密(2):AES代码实现解析
在我的上一篇文章AES基础知识和计算过程中,大概介绍了AES(Rijndael)加密的整个过程。那么在这一篇文章中,就来看一下AES在代码中是如何实现的,也有助于我们理解其中的一些细节。 本篇文章所用的AES代码来源于Szymon Stefanek的开源C代码 文章…...

SpringBoot项目通过分词器生成词云
目录 前言一、词云是什么?二、使用步骤1.引入依赖2.application.yml3.Controller4.分词工具类4.词云生成工具类、支持输出文件和字节流 注意 前言 公司项目涉及到员工任务管理,需要从员工任务中获取任务信息生成个人词云图,可以把员工任务中…...

Nacos 配置管理及相关使用
文章目录 Nacos 配置管理一、统一配置管理1、在Nacos 中添加配置文件2、从微服务拉取配置3、配置实现步骤(1)引入 nacos-config 依赖(2)添加 bootstrap.yml(4)在 nacos 中添加配置 二、配置热更新1、配置热…...

重发布与路由策略
华子目录 重发布重发布条件重发布配置规则重发布名词配置命令ospf往rip重发布(重发布动态)静态往rip重发布(重发布静态)直连往rip重发布(重发布直连)rip往ospf重发布(重发布动态)静态…...
)
57. 插入区间(C++题解)
57. 插入区间 插入区间 给你一个无重叠的 ,按照区间起始端点排序的区间列表。 在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。 示例 1: 输入&#x…...

【数据结构Java版】 初识泛型和包装类
目录 1.包装类 1.1基本数据类型以及它们所对应的包装类 1.2装箱和拆箱 1.3自动装箱和自动拆箱 2.什么是泛型 3.引出泛型 4.泛型类的使用 4.1语法 4.2示例 4.3类型推导 5.泛型是如何编译的 5.1擦除机制 5.2正确的写法 6.泛型的上届 6.1语法 6.2示例 …...

Spring中如何解决循环依赖问题的三种方法
什么是循环依赖问题 在 Spring 中,循环依赖问题指的是两个或多个 bean 之间相互依赖形成的闭环。具体而言,当 bean A 依赖于 bean B,同时 bean B 也依赖于 bean A,就形成了循环依赖。 循环依赖问题在 Spring 容器中是一个非常常…...
【ArcGIS Pro二次开发】(65):进出平衡SHP转TXT、TXT转SHP
最近一个小伙伴提了这么一个需求,需要把TXT和SHP进行互转。 这种TXT文件其实遇到了好几个版本,都有一点小差异。之前已经做过一个TXT转SHP的工具,但好像不适用。于是针对这个版本,做了互转的2个工具。 【SHP转TXT】 一、要实现的…...

Shell开发实践:服务器的磁盘、CPU、内存的占用监控
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌,CSDN博客专家,阿里云社区专家博主,2023年6月CSDN上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师…...
)
超详细 async和await 项目实战运用(附加文字解答+源码)
文章目录 问题描述async什么是 asyncasync 的作用async 的应用场景async 优点 await什么是 awaitawait 的作用await 的应用场景await 的优点async和 await结合使用 结束语 大家好!又到了愉快的周末假期,今天是2023年9月3日|农历七月十九,我最…...
Maven入门教程(三):Maven语法
视频教程:Maven保姆级教程 Maven入门教程(一):安装Maven环境 Maven入门教程(二):idea/Eclipse使用Maven Maven入门教程(三):Maven语法 Maven入门教程(四):Nexus私服 Maven入门教程(五):自定义脚手架 6.Mav…...

C++技术点,故事解析
语言的魅力 从人类诞生开始 ,南方古猿到现代人类经历了非常多变化; 南方古猿到能人 有什么变化? 能人会使用工具,由于会使用工具 就可以获得肉类食物,当然只能吃一些动物腐肉 直到进化成直立人的晚期,在东…...
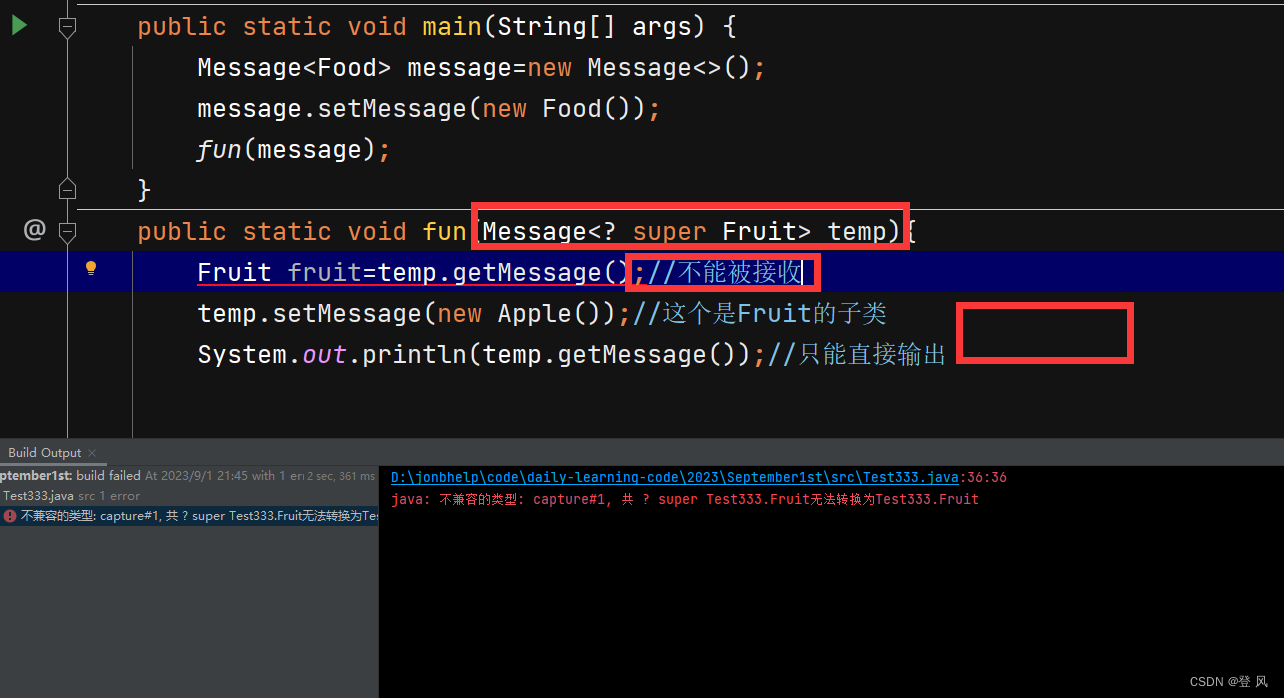
数据结构(Java实现)-字符串常量池与通配符
字符串常量池 在Java程序中,类似于:1, 2, 3,3.14,“hello”等字面类型的常量经常频繁使用,为了使程序的运行速度更快、更节省内存,Java为8种基本数据类型和String类都提供了常量池。…...

python强化学习--gym安装与使用
最近开始学习强化学习,第一步肯定是要学会安装和使用pym,原本以为很简单,事实上确实很简单,但是遇到一个小问题,就是安装gym之后,在应用的过程中,游戏界面没有显示出来,了解后才知道…...
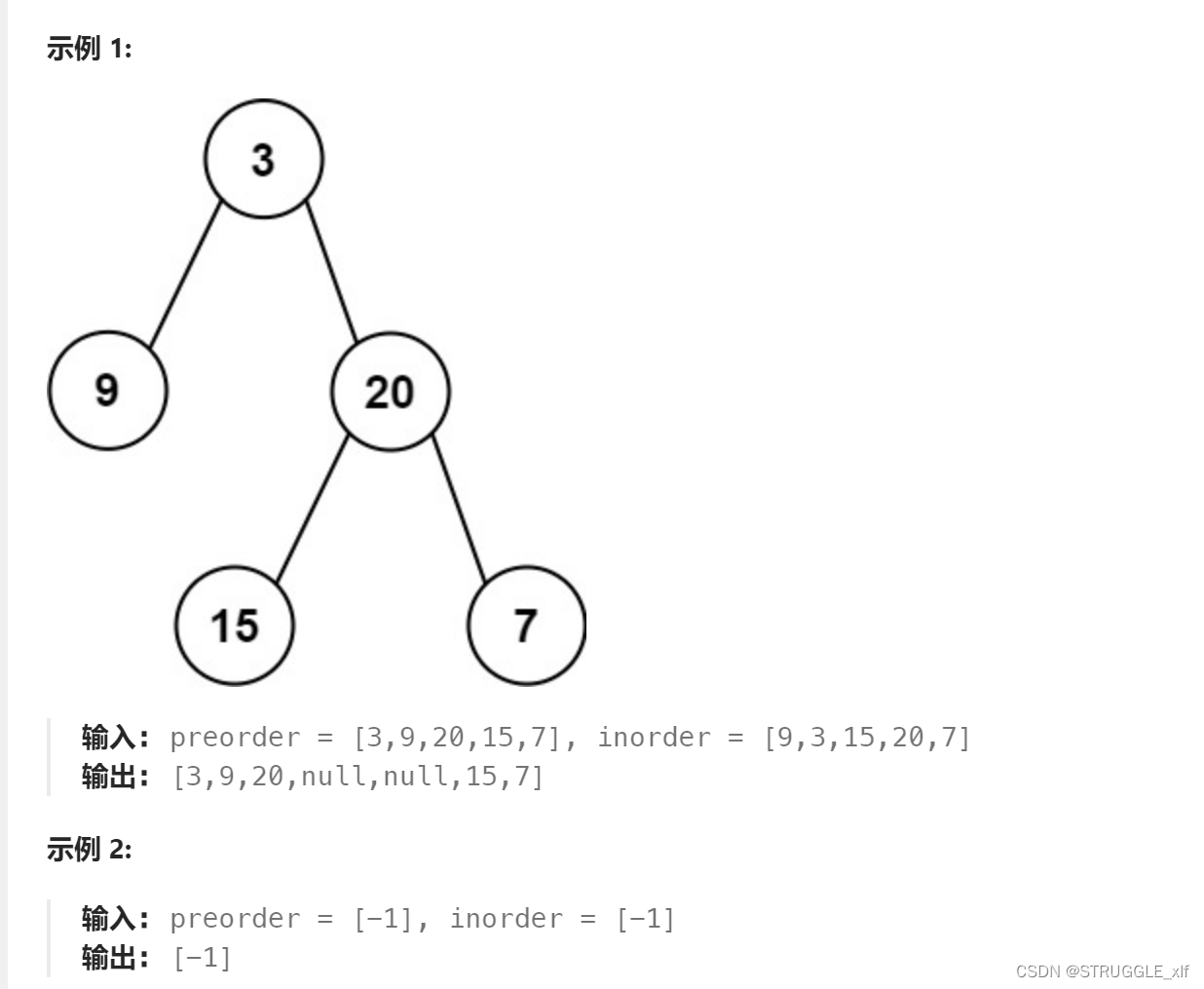
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。 思路:题目给出了先序遍历和中序遍历的结果,因为先序遍历遵循根–>左–>…...

(第六天)初识Spring框架-SSM框架的学习与应用(Spring + Spring MVC + MyBatis)-Java EE企业级应用开发学习记录
SSM框架的学习与应用(Spring Spring MVC MyBatis)-Java EE企业级应用开发学习记录(第六天)初识Spring框架 昨天我们已经把Mybatis框架的基本知识全部学完,内容有Mybatis是一个半自动化的持久层ORM框架,深入学习编写动态SQL&a…...
如何使用『Nginx』配置后端『HTTPS』协议访问
前言 本篇博客主要讲解如何使用 Nginx 部署后端应用接口 SSL 证书,从而实现 HTTPS 协议访问接口(本文使用公网 IP 部署,读者可以自行替换为域名) 申请证书 须知 请在您的云服务平台申请 SSL 证书,一般来说证书期限…...
Git仓库简介
1、工作区、暂存区、仓库 工作区:电脑里能看到的目录。 暂存区:工作区有一个隐藏目录.git,是Git的版本库,Git的版本库里存了很多东西,其中最重要的就是称为stage(或者叫index)的暂存区…...

TensorRTC++ | INT8量化
Int8量化步骤 // 这是基本需要的组件 auto builder = make_nvshared(nvinfer1::createInferBuilder(logger)); auto config = make_nvshared(builder->createBuilderConfig())...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
