2024王道408数据结构P144 T18
2024王道408数据结构P144 T18
思考过程
- 首先还是先看题目的意思,让我们在中序线索二叉树里查找指定结点在后序的前驱结点,这题有一点难至少对我来说…我讲的不清楚理解一下我做的也有点糊涂。
- 在创建结构体时多两个变量ltag和rtag,当ltag=0时就说明该结点有左孩子,当ltag=1时说明该结点的lchild指向它的前驱结点。
- 那么我们需要把一个二叉树给中序线索化,线索化后假设有这么一颗二叉树
 之后要查找指定结点在后序的前驱结点有这么五种情况,假设指定结点为指针p:
之后要查找指定结点在后序的前驱结点有这么五种情况,假设指定结点为指针p: - 如果p有右孩子,那么在后序的前驱结点也就是该结点的右孩子,
if(p->rtag==0)从上面那个二叉树来看很明显。 - 如果p没有右孩子但是有左孩子,那么在后序的前驱结点也就是改结点的左孩子,
if(p->ltag==0)比如上图的结点B,当B没有右孩子但是有左孩子时,在后序序列中的前驱结点也就是它的左孩子D。 - 如果p是中序遍历中的第一个结点的话,那么在后序遍历中也必定是第一个结点,
if (p->lchild==NULL)这时候也就说明该结点没有前驱结点,我们直接q=NULL就好了。 - 第四种情况就是该结点没有左右孩子,比如下图这种情况
 这棵树中的C结点就是没有左右孩子的,此时它在后序序列中的前驱结点就是先要找到该结点的祖先,
这棵树中的C结点就是没有左右孩子的,此时它在后序序列中的前驱结点就是先要找到该结点的祖先,while (p->ltag == 1 && p->lchild != NULL) p = p->lchild;找到祖先后那也就是该祖先结点的左孩子。if (p->ltag == 0) q = p->lchild; - 那最后一种情况就是一棵树中既没有左孩子也没有右孩子,只有一个孤零零的结点,此时也就是
q=NULL;了
- 如果p有右孩子,那么在后序的前驱结点也就是该结点的右孩子,
完整代码
//
// Created by 黎圣 on 2023/8/29.
//
//在中序线索二叉树里查找指定结点在后序的前驱结点
#include "iostream"
using namespace std;
typedef struct TreeNode
{char data;struct TreeNode *lchild, *rchild;int ltag, rtag;
}*tree;
void CreateTree(tree &t)
{char ch = getchar();if (ch == '#')t = NULL;else{t = (struct TreeNode *)malloc(sizeof(struct TreeNode));t->data = ch;t->lchild = NULL;t->rchild = NULL;t->ltag = t->rtag = 0;CreateTree(t->lchild);CreateTree(t->rchild);}
}
struct TreeNode *pre;
void zx(tree &t)
{if (t){zx(t->lchild);if (t->lchild == NULL){t->ltag = 1;//无左孩子t->lchild = pre;}elset->ltag = 0;//有左孩子if (pre != NULL && pre->rchild == NULL){pre->rtag = 1;pre->rchild = t;}pre = t;zx(t->rchild);}
}
tree Inpostpre(tree &t, struct TreeNode *p)
{struct TreeNode *q;//结果指针if (p->rtag == 0)//有右孩子就是右孩子q = p->rchild;else if (p->ltag == 0)//没有右孩子有左孩子就是左孩子q = p->lchild;else if (p->lchild == NULL)q = NULL;else{while (p->ltag == 1 && p->lchild != NULL)p = p->lchild;//若找到祖先结点 且有左孩子 结果就是左孩子if (p->ltag == 0)q = p->lchild;elseq = NULL;}return q;
}
int main()
{tree t;CreateTree(t);//ABD##E##CF##G##zx(t);printf("%c ", Inpostpre(t, t->rchild)->data);return 0;
}
相关文章:

2024王道408数据结构P144 T18
2024王道408数据结构P144 T18 思考过程 首先还是先看题目的意思,让我们在中序线索二叉树里查找指定结点在后序的前驱结点,这题有一点难至少对我来说…我讲的不清楚理解一下我做的也有点糊涂。在创建结构体时多两个变量ltag和rtag,当ltag0时…...

在windows下安装配置skywalking
1.下载地址 Downloads | Apache SkyWalkinghttp://skywalking.apache.org/downloads/ 2.文件目录说明 将文件解压后,可看到agent和bin目录: Agent:作为探针,安装在服务器端,进行数据采集和上报。 Config:…...
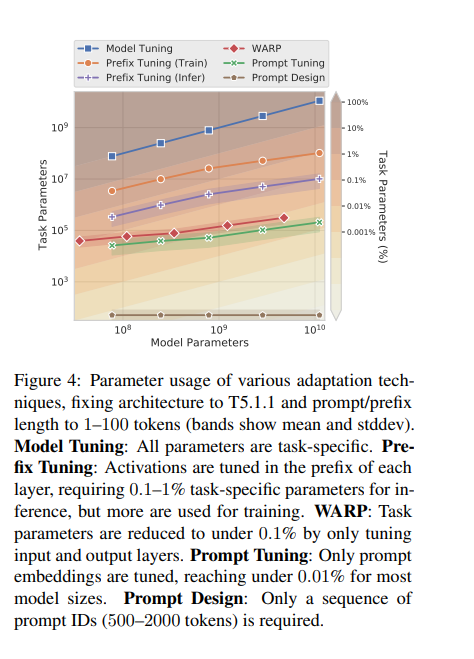
关于大模型参数微调的不同方法
Adapter Tuning 适配器模块(Adapter Moudle)可以生成一个紧凑且可扩展的模型;每个任务只需要添加少量可训练参数,并且可以在不重新访问之前任务的情况下添加新任务。原始网络的参数保持不变,实现了高度的参数共享 Pa…...
)
方法的引用第一版(method reference)
1、体验方法引用 在使用Lambda表达式的时候,我们实际上传递进去的代码就是一种解决方案:拿参数做操作那么考虑一种情况:如果我们在Lanbda中所指定的操作方案,已经有地方存在相同方案,那是否还有必要再重复逻辑呢&#…...

Android DataBinding 基础入门(学习记录)
目录 一、DataBinding简介二、findViewById 和 DataBinding 原理及优缺点1. findViewById的优缺点2. DataBinding的优缺点 三、Android mvvm 之 databinding 原理1. 简介和三个主要的实体DataViewViewDataBinding 2.三个功能2.1. rebind 行为2.2 observe data 行为2.3 observe …...

spring 错误百科
一、使用Spring出错根源 1、隐式规则的存在 你可能忽略了 Sping Boot 中 SpringBootApplication 是有一个默认的扫描包范围的。这就是一个隐私规则。如果你原本不知道,那么犯错概率还是很高的。类似的案例这里不再赘述。 2、默认配置不合理 3、追求奇技淫巧 4、…...
OpenCV基本操(IO操作,读取、显示、保存)
图像的IO操作,读取和保存方法 1.1 API cv.imread()参数: 要读取的图像 读取图像的方式: cv.IMREAD*COLOR:以彩色模式加载图像,任何图像的图像的透明度都将被忽略。这是默认参数 标志: 1 cv.IMREAD*GRAYSCALE :以…...

1.快速搭建Flask项目
一.Pear Admin Flask 官网文档:http://www.pearadmin.com/doc/index.html 1.1下载安装 # 下 载 git clone https://gitee.com/pear-admin/pear-admin-flask# 安 装 pip install -r requirements.txt1.2修改配置 applications下的config.py docker运行的修改dockerdata/conf…...

编程题四大算法思想(三)——贪心法:找零问题、背包问题、任务调度问题、活动选择问题、Prim算法
文章目录 贪心法找零问题(change-making problem)贪心算法要求基本思想适合求解问题的特征 背包问题0/1背包问题0/1背包问题——贪心法 分数背包问题 任务调度问题活动选择问题活动选择——贪心法最早结束时间优先——最优性证明 Prim算法 贪心法 我在当…...
core dump管理在linux中的前世今生
目录 一、什么是core dump? 二、coredump是怎么来的? 三、怎么限制coredump文件的产生? ulimit 半永久限制 永久限制 四、从源码分析如何对coredump文件的名字和路径管理 命名 管理 一些问题的答案 1、为什么新的ubuntu不能产生c…...

Springboot整合knife4j配置swagger教程-干货
开启swagger文档,直接上教程。 第一步:引入依赖 <!--swagger 依赖--><dependency><groupId>com.github.xiaoymin</groupId><artifactId>knife4j-spring-boot-starter</artifactId><version>3.0.3</version></d…...

C++ 中的 Pimpl 惯用法
C 中的 Pimpl 惯用法 介绍 Pimpl(Pointer to Implementation)是一种常见的 C 设计模式,用于隐藏类的实现细节,从而减少编译依赖和提高编译速度。本文将通过一个较为复杂的例子,展示如何使用智能指针(如 s…...

【个人博客系统网站】统一处理 · 拦截器
【JavaEE】进阶 个人博客系统(2) 文章目录 【JavaEE】进阶 个人博客系统(2)1. 统一返回格式处理1.1 统一返回类common.CommonResult1.2 统一返回处理器component.ResponseAdvice 2. 统一异常处理3. 拦截器实现3.1 全局变量SESSI…...
)
深入探索PHP编程:文件操作与输入/输出(I/O)
深入探索PHP编程:文件操作与输入/输出(I/O) 在PHP编程中,文件操作和输入/输出(I/O)是不可或缺的关键部分。无论是读取、写入文件,还是处理上传的文件,这些操作都是Web开发的重要组成…...

基于jeecg-boot的flowable流程自定义业务驳回到发起人的一种处理方式
有些粉丝,希望对自定义业务中,驳回到发起人进行处理,比如可以重新进行发起流程,下面就给出一种方式,当然不一定是最好的方式,只是提供一种参考而已,以后可以考虑动态根据流程状态或节点信息进行…...

【大数据知识】大数据平台和数据中台的定义、区别以及联系
数据行业有太多数据名词,例如大数据、大数据平台、数据中台、数据仓库等等。但大家很容易混淆,也很容易产生疑问,今天我们就来简单聊聊大数据平台和数据中台的定义、区别以及联系。 大数据平台和数据中台的定义 大数据平台:一个…...

华为OD:IPv4地址转换成整数
题目描述: 存在一种虚拟IPv4地址,由4小节组成,每节的范围为0-255,以#号间隔,虚拟IPv4地址可以转换为一个32位的整数,例如: 128#0#255#255,转换为32位整数的结果为2147549183&#…...
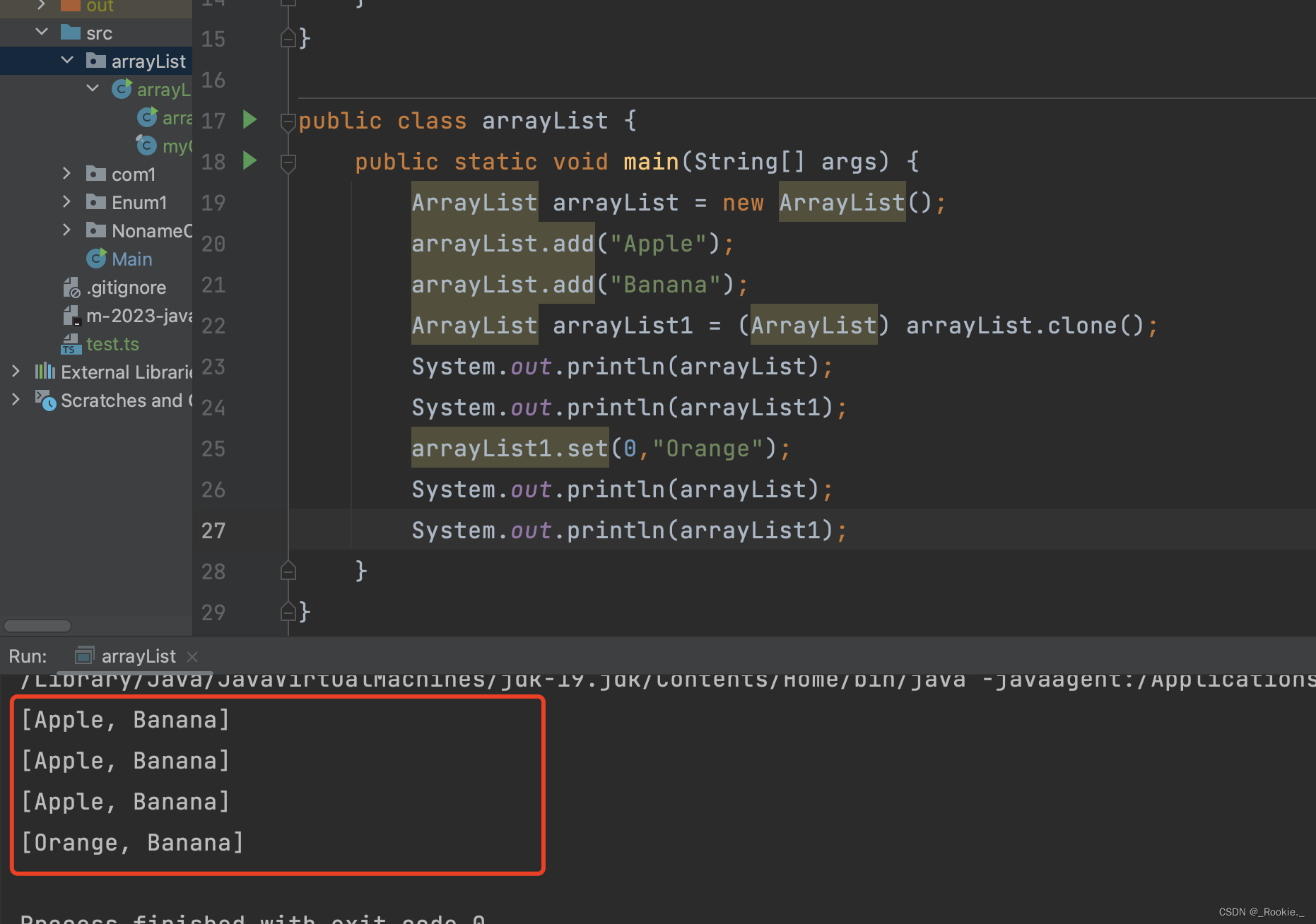
2023.9 - java - 浅拷贝
与 js的浅拷贝不同: 在 JavaScript 中, Object.assign() 或 spread 运算符等方法可以实现浅拷贝,但只针对对象的第一层属性进行复制。如果一个对象只包含基本数据类型的属性,那么对浅拷贝出来的对象进行修改不会影响原始对象&…...
STM32f103入门(10)ADC模数转换器
ADC模数转换器 ADC简介AD单通道初始化代码编写第一步开启时钟第二步 RCCCLK分频 6分频 72M/612M第三步 配置GPIO 配置为AIN状态第四步,选择规则组的输入通道第五步 用结构体 初始化ADC第六步 对ADC进行校准编写获取电压函数初始化代码如下 Main函数编写 ADC简介 ADC…...

实训笔记8.28
实训笔记8.28 8.28笔记一、大数据计算场景主要分为两种1.1 离线计算场景1.2 实时计算场景 二、一般情况下大数据项目的开发流程2.1 数据采集存储阶段2.2 数据清洗预处理阶段2.3 数据统计分析阶段2.4 数据挖掘预测阶段2.5 数据迁移阶段2.6 数据可视化阶段 三、纯大数据离线计算项…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
