C++,菱形继承和虚继承
一、菱形继承的基本概念
菱形继承又称为钻石继承,由公共基类派生出多个中间子类,又由多个中间子类共同派生出汇聚子类。汇聚子类会得到,中间子类从公共基类继承下来的多份成员。
菱形继承的格式:
A --------公共基类/ \B C ------- 中间子类\ /D --------汇聚子类示例:
#include <iostream>
using namespace std;//封装公共基类 家具 类
class Jiaju
{
private:string color;
public://无参构造Jiaju() {cout << "家具的无参构造函数" << endl;}//有参构造Jiaju(string n):color(n){cout << "家具的有参构造函数" << endl;}
};//中间子类
//封装 沙发的类
class Sofa:public Jiaju
{
private:string sitting;
public://无参构造Sofa() {cout << "沙发的无参构造" << endl;}//有参构造函数Sofa(string s,string c):Jiaju(c),sitting(s){cout << "沙发的有参构造" << endl;}void display(){cout << sitting << endl;}
};//中间子类
//封装 床 类
class Bed:public Jiaju
{
private:string sleep;public://无参Bed() {cout << "床的无参构造" << endl;}//有参Bed(string s,string c):Jiaju(c),sleep(s){cout << "床的有参构造" << endl;}void display(){cout << sleep << endl;}
};//汇聚子类
//封装 沙发床类 继承于沙发 和 床
class Sofa_Bed:public Bed,public Sofa
{
private:int w;
public://Sofa_Bed(){cout << "沙发床的无参构造" << endl;}//有参构造Sofa_Bed(string sit, string s, int w,string c):Bed(s,c),Sofa(sit,c),w(w){cout << "沙发床的有参构造" << endl;}
};int main()
{
// Sofa_Bed s;Sofa_Bed s1("可坐","可躺",123,"pink");return 0;
}菱形继承存在的问题:
汇聚子类会得到,中间子类从公共基类继承下来的多份成员,造成空间浪费,没有必要,还会对公共基类的成员多次初始化,或释放。
二、虚继承
虚继承的作用:
可以让汇聚子类只保留一份 中间子类从公共基类继承下来的成员。
虚继承的格式:
在中间子类的继承方式前 加上 virtual
class 类名 : virtual 继承方式 类名 //中间子类
{中间子类的拓展;
};使用虚继承的注意事项:
中间子类虚继承公共基类后,汇聚子类的初始化列表,先调用中间子类的有参构造函数,中间子类再调用公共基类的有参构造函数。但是,虚继承之后,只保留一份中间子类从公共基类继承下来的有参构造函数,意味着不知道调用哪一个中间子类继承下来的公共基类的构造函数,这样就会默认调用公共基类的无参构造函数。
如果汇聚子类想要对公共基类的数据成员初始化,需要显性调用公共基类的构造函数。
示例:
#include <iostream>
using namespace std;//封装公共基类 家具 类
class Jiaju
{
private:string color;
public://无参构造Jiaju() {cout << "家具的无参构造函数" << endl;}//有参构造Jiaju(string n):color(n){cout << "家具的有参构造函数" << endl;}
};//中间子类
//封装 沙发的类
class Sofa:virtual public Jiaju //中间子类虚继承公共基类
{
private:string sitting;
public://无参构造Sofa() {cout << "沙发的无参构造" << endl;}//有参构造函数Sofa(string s,string c):Jiaju(c),sitting(s){cout << "沙发的有参构造" << endl;}void display(){cout << sitting << endl;}
};//中间子类
//封装 床 类
class Bed:virtual public Jiaju //中间子类虚继承公共基类
{
private:string sleep;public://无参Bed() {cout << "床的无参构造" << endl;}//有参Bed(string s,string c):Jiaju(c),sleep(s){cout << "床的有参构造" << endl;}void display(){cout << sleep << endl;}
};//汇聚子类
//封装 沙发床类 继承于沙发 和 床
class Sofa_Bed:public Bed,public Sofa
{
private:int w;
public://Sofa_Bed(){cout << "沙发床的无参构造" << endl;}//有参构造Sofa_Bed(string sit, string s, int w,string c):Jiaju(c),Bed(s,c),Sofa(sit,c),w(w) //需要在汇聚子类中显性调用公共基类的有参构造函数{cout << "沙发床的有参构造" << endl;}
};int main()
{
// Sofa_Bed s;Sofa_Bed s1("可坐","可躺",123,"pink");return 0;
}相关文章:

C++,菱形继承和虚继承
一、菱形继承的基本概念 菱形继承又称为钻石继承,由公共基类派生出多个中间子类,又由多个中间子类共同派生出汇聚子类。汇聚子类会得到,中间子类从公共基类继承下来的多份成员。 菱形继承的格式: A --------公共基类/ \…...

js实现一行半文本的截取
最近遇到一个需求是要在第二行的中间截取文本,因为在后面得贴一个图标,所以这种情况用常规的css截取文本有点难处理。于是在上网查阅后发现了几个方法:第一种是用伪元素加定位,把.;11..盖在文字的上面;第二…...

计算一个区间时间差值,时间保留剩下的差值
解决目的 begin end,去除集合类的其他区间差值List<rang> r1 new ArrayList(); 得到差值package com.jowoiot.wmzs.utils.date;import com.google.common.collect.Lists; import com.google.common.collect.Range; import org.apache.commons.lang.time.Dat…...

uniapp 微信小程序添加隐私保护指引
隐私弹窗: <uni-popup ref"popup"><view class"popupWrap"><view class"popupTxt">在你使用【最美万年历】之前,请仔细阅读<text class"blueColor" click"handleOpenPrivacyContract…...
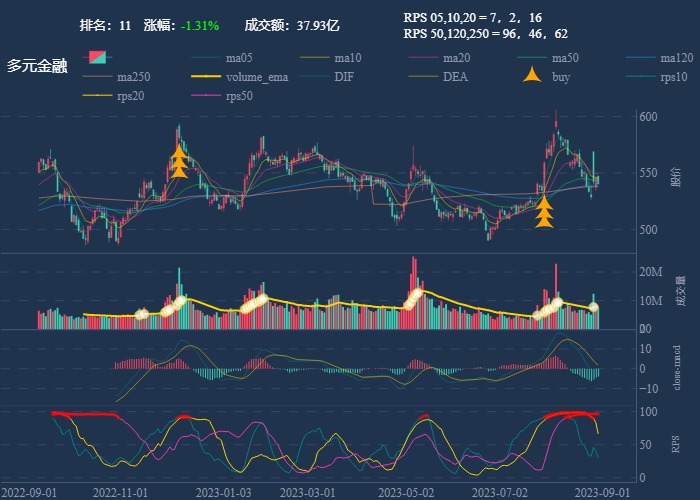
行业追踪,2023-08-30
自动复盘 2023-08-30 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
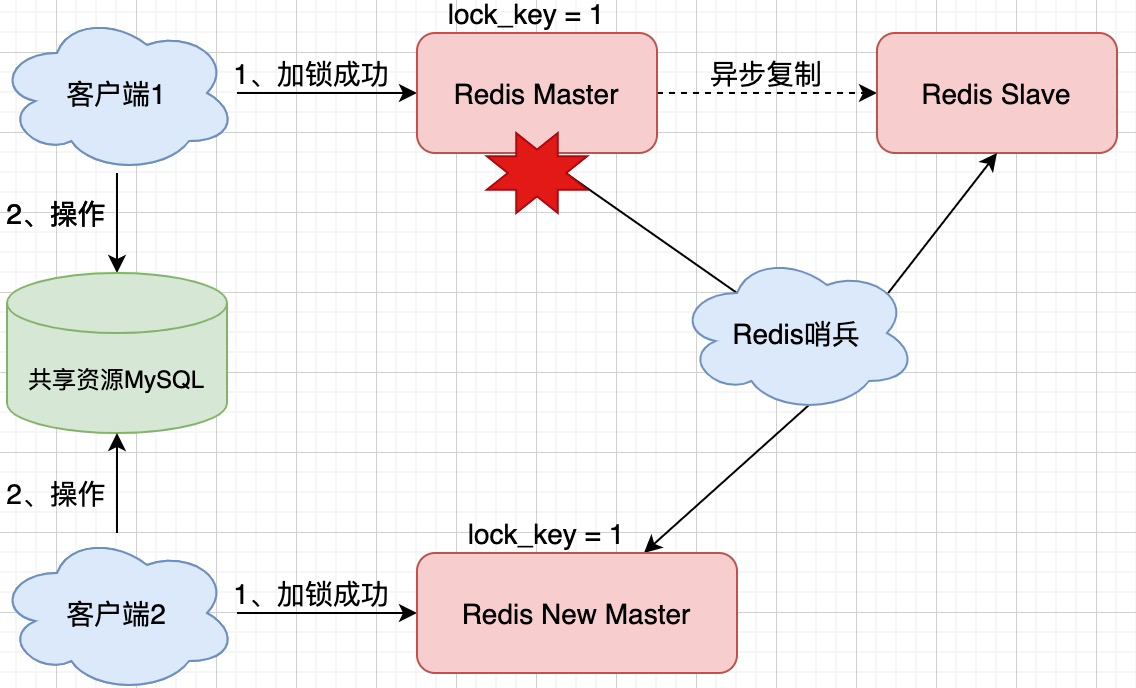
Redis——》Redis的部署方式对分布式锁的影响
推荐链接: 总结——》【Java】 总结——》【Mysql】 总结——》【Redis】 总结——》【Kafka】 总结——》【Spring】 总结——》【SpringBoot】 总结——》【MyBatis、MyBatis-Plus】 总结——》【Linux】 总结——》【MongoD…...

VTK——使用包围盒切割医学图像
VTK 库 vtkDICOMImageReader:专门用于读取医学图像格式 DICOM 的类。DICOM(Digital Imaging and Communications in Medicine)是医学图像和信息的标准。 vtkImageGaussianSmooth:用于图像的高斯平滑处理,主要用于去噪…...

在工具提示中使用自绘修改字体
在上一篇文章中,我们学习了如何在应用程序中添加工具提示。在之前的例子代码中,我们通过简单地为创建的工具提示设置了目标字体,这种方法很简单,因为自始至终,我们都只创建了一个工具提示。 但是,如果在应…...

【Git管理工具】使用Docker部署GitLab服务器
【Git管理工具】使用Docker部署GitLab服务器 一、GitLab介绍1.1 GitLab简介1.2 GitLab特点二、本次实践介绍2.1 本地环境规划2.2 本次实践介绍三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本三、Docker CompseV2版本升级(可选)3.1 创建…...
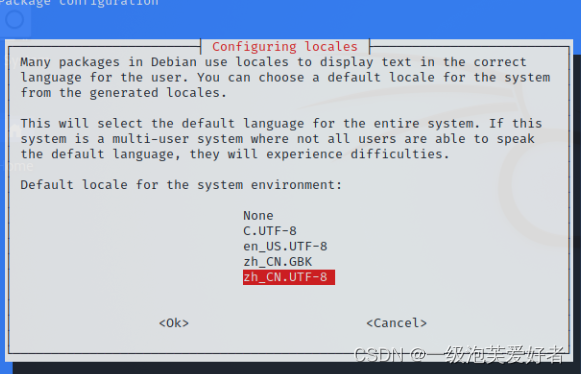
安装kali虚拟机镜像的坑
1.0 安装虚拟机镜像成功之后,只有光标,没有界面 在VMware上安装kali linux环境时,根据提示操作完成后,开启虚拟机,屏幕黑屏,左上角有一个光标在闪,一直开不了机。 出现问题的原因,…...

【Android】TextView适配文本大小并保证中英文内容均在指定的UI 组件内部
问题 现在有一个需求,在中文环境下textView没有超过底层的组件限制,但是一切换到英文环境就超出了,这个如何解决呢?有啥例子吗? 就像这样子的。 解决 全部代码如下: <?xml version"1.0"…...
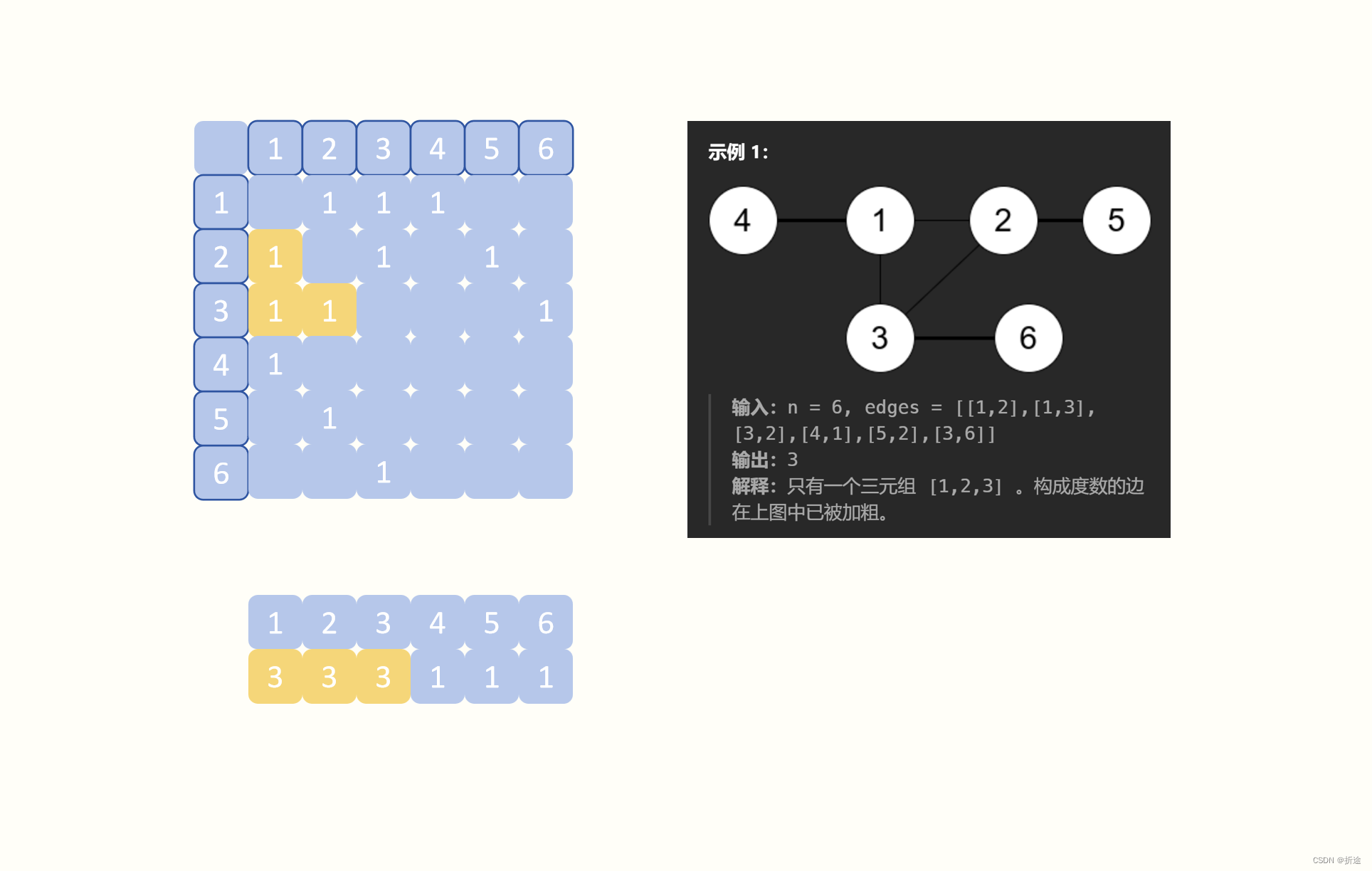
【力扣每日一题】2023.8.31 一个图中连通三元组的最小度数
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 题目给我们一个无向图,要我们找出三个节点,这三个节点他们两两相连,这三个节点除了连接到对方的其他线…...

C语言--volatile
volatile 1、介绍 volatile是一个类型修饰符(type specifier)。它是被设计用来修饰被不同线程访问和修改的变量。如果没有volatile,基本上会导致这样的结果:要么无法编写多线程程序,要么编译器失去大量优化的机会。 …...

技术深入解析与教程:网络安全技术探秘
第一章:引言 在当今数字化时代,网络安全已经成为了重要议题。随着各种信息和业务在网络上的传输与存储,安全问题也日益突出。本文将带您深入探讨网络安全领域中的关键技术,涵盖渗透测试、漏洞挖掘以及恶意软件分析等方面…...
Android studio 实现生成二维码和扫描二维码
效果图 build.gradle(:app)添加依赖 dependencies {implementation com.google.zxing:core:3.3.3implementation com.journeyapps:zxing-android-embedded:3.6.0implementation com.google.zxing:javase:3.0.0 }Manifests.xml <uses-permission android:name"android…...

Linux中7种文件类型
Linux中文件类型 Linux中一切皆为文件。 查看文件类型(输入以下命令根据第一列的第一个字符可区别文件类型) ls -l目录文件 第一个字符为d 类似于Windows文件夹。 链接文件(软链接) 第一个字符为l 例如Windows的快捷方式&…...

基础算法--快速排序
快速排序 算法原理 1. 取一个元素p(第一个元素,最后一个元素,中间元素,随机 都可以),使元素p归位。 2. 列表被p分成两部分,左边都比p小,右边都比p大。 3. 递归完成排序。 动态演示 python代码实现 import…...

机器学习的第一节基本概念的相关学习
目录 1.1 决策树的概念 1.2 KNN的概念 1.2.1KNN的基本原理 1.2.2 流程: 1.2.3 优缺点 1.3 深度学习 1.4 梯度下降 损失函数 1.5 特征与特征选择 特征选择的目的 1.6 python中dot函数总结 一维数组的点积: 二维数组(矩阵)的乘法&am…...

Python 之__name__的用法以及解释
文章目录 介绍代码 介绍 __name__ 是一个在 Python 中特殊的内置变量,用于确定一个 Python 文件是被直接运行还是被导入为模块。 文件作为模板导入,则其 __name__属性值被自动设置为模块名 文件作为程序直接运行,则__name__属性属性值被自动设…...

【FPGA零基础学习之旅#12】三线制数码管驱动(74HC595)串行移位寄存器驱动
🎉欢迎来到FPGA专栏~三线制数码管驱动 ☆* o(≧▽≦)o *☆嗨~我是小夏与酒🍹 ✨博客主页:小夏与酒的博客 🎈该系列文章专栏:FPGA学习之旅 文章作者技术和水平有限,如果文中出现错误,希望大家能指…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
