【数据结构】树和二叉树的概念及结构(一)
目录
一,树的概念及结构
1,树的定义
2,树结点的分类及关系
3,树的表示
二,二叉树的概念及结构
1,二叉树的定义
2,特殊的二叉树
3,二叉树的性质
4,二叉树的存储结构
1,顺序存储
2,链式储存
一,树的概念及结构
1,树的定义
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
树(Tree)是n(n>=0)个结点的有限集;
n=0时称为空树;
在任意一颗非空树中:
1,有且仅有一个特定的称为根(Root)的结点;
2,当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,......,Tm,其中每一个集合本身又是一棵树,并且称为跟的子树(SubTree);
如下图所示:

注意:树形结构中,子树之间不能有交集,否则就不是树形结构

2,树结点的分类及关系

结点的度:一个结点含有的子树的个数称为该结点的度; 如上图:A的为4
叶结点或终端结点:度为0的结点称为叶结点; 如上图:K,G,L,M,N...等结点为叶结点
非终端结点或分支结点:度不为0的结点; 如上图:B,C,E...等结点为分支结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父节点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
树的度:一棵树中,最大的结点的度称为树的度; 如上图:树的度为4
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为堂兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先,C是G,H的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙,G,H是C的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
3,树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};图解:

二,二叉树的概念及结构
1,二叉树的定义
二叉树(Binary Tree)是n(n>=0) 个结点的有限集合;
该集合或者为空集(称为空二叉树);
或者由一个根结点和两颗互不相交的,分别为根结点的左子树和右子树的二叉树组成;
图示:
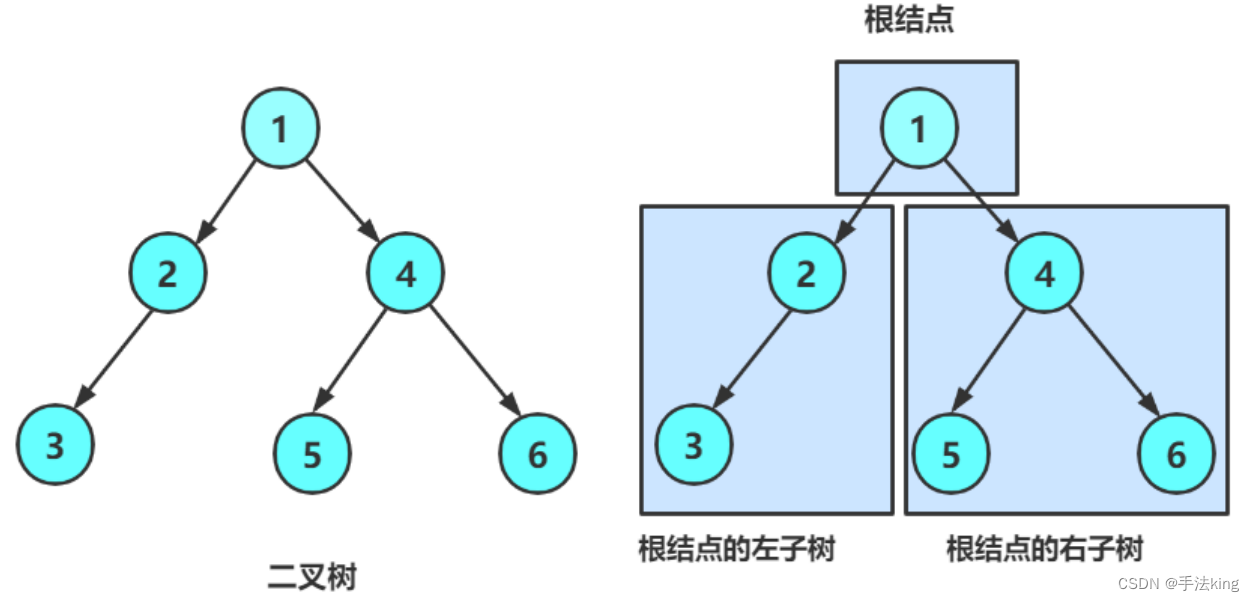
由上图可以看出:
1,二叉树不存在度大于2的结点
2,二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
二叉树具有以下五种基本形态:

2,特殊的二叉树
1,斜树
所有的结点都只有左子树的二叉树叫左斜树;
所有的结点都只有右子树的二叉树叫右斜树;
斜树图示:

2,满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是2^k-1 ,则它就是满二叉树

3,完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对 应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树

3,二叉树的性质
1,若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点
2,若规定根结点的层数为1,则深度为h的二叉树的最大结点数是 2^h-1
3,对任何一棵二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n1 ,则有 n0=n1+1
4,若规定根结点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1)
5,对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有结点从0开始编号,则对于序号为i的结点有:
1,若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2,若2i+1<n,左孩子序号:2i+1
3,若2i+1>n,右孩子序号:2i+2
4,二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构
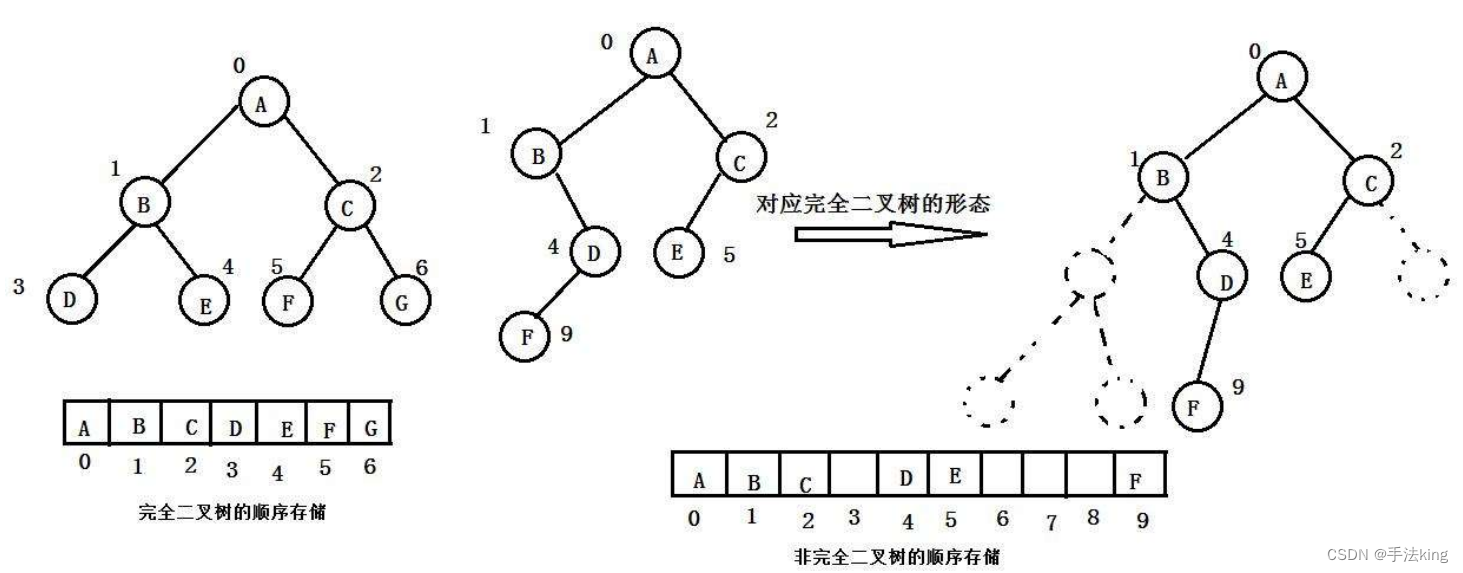
1,顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储
二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
2,链式储存
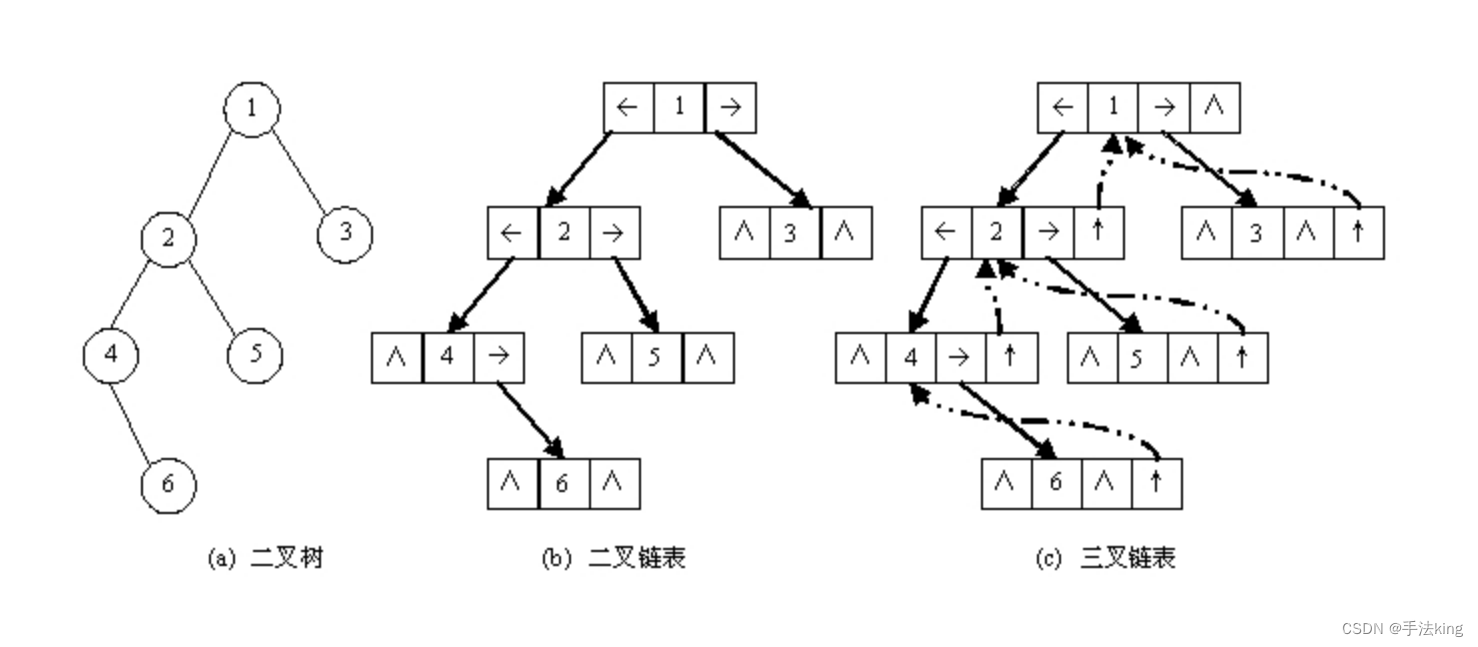
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系;
通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址;
链式结构又分为二叉链和三叉链
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向当前节点的双亲struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};
第一阶段就到这里了,带大家先了解一下树和二叉树的原理;
后面博主会陆续更新;
如有不足之处欢迎来补充交流!
完结。。。
相关文章:

【数据结构】树和二叉树的概念及结构(一)
目录 一,树的概念及结构 1,树的定义 2,树结点的分类及关系 3,树的表示 二,二叉树的概念及结构 1,二叉树的定义 2,特殊的二叉树 3,二叉树的性质 4,二叉树的存储结构 1&…...
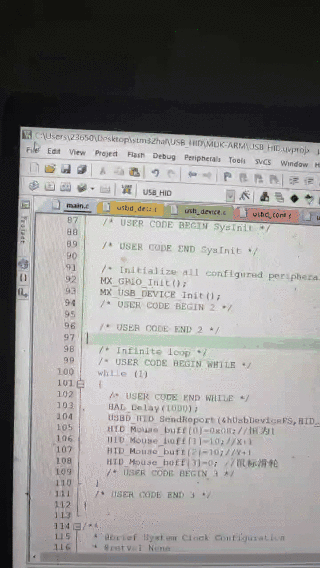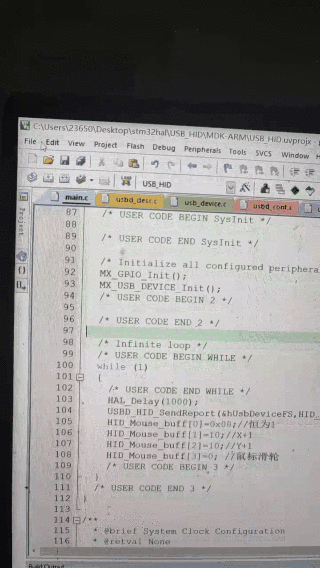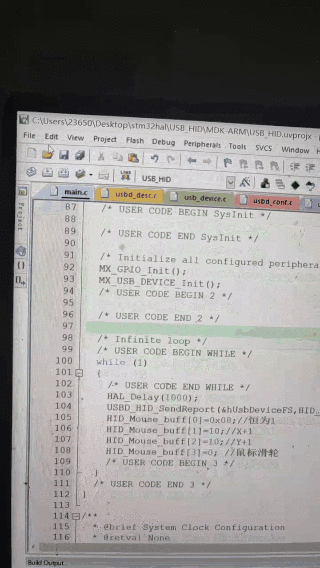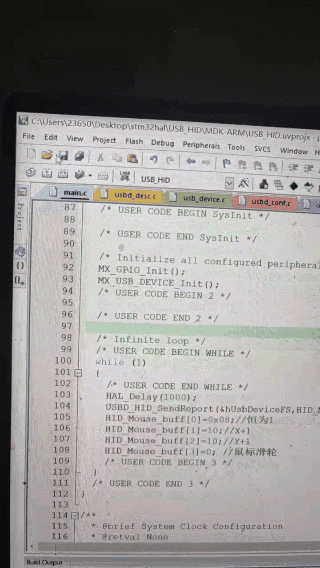
第三章 USB应用笔记之USB鼠标(以STM32 hal库为例)
第三章 USB应用笔记之USB鼠标(以STM32 hal库为例) 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 第三章 USB应用笔记之USB鼠标(以STM32 hal库为例)前言一、STM32 U…...

微服务01-基本介绍+注册中心EureKa
基本介绍 服务集群:一个请求由多个服务完成,服务接口暴露,以便于相互调用; 注册中心:每个服务的状态,需要进行维护,我们可以在注册中心进行监控维护服务; 配置中心:这些…...

【ES6】JavaScript中的异步编程:async和await
在JavaScript中,异步编程是一种处理长时间运行的操作的方法,这些操作包括读取文件、网络请求或处理大数据等。在传统的回调函数中,代码按照顺序执行,一旦遇到长时间运行的操作,就需要回调函数来处理结果。这使得代码变…...
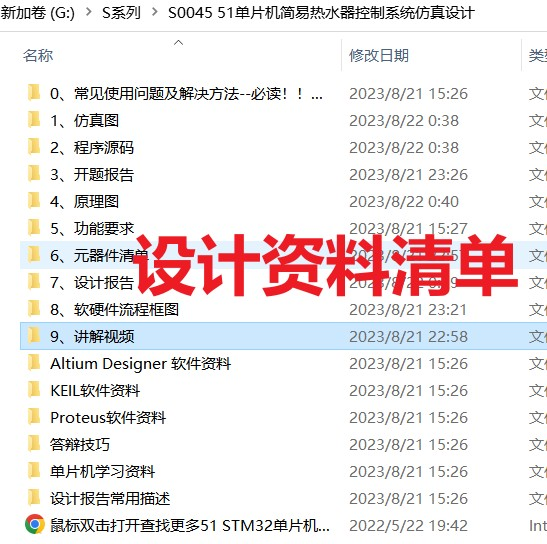
51单片机热水器温度控制系统仿真设计( proteus仿真+程序+原理图+报告+讲解视频)
51单片机热水器温度控制系统仿真设计 1.主要功能:2.仿真3. 程序代码4. 原理图5. 设计报告6. 设计资料内容清单 &&下载链接 51单片机热水器温度控制系统仿真设计( proteus仿真程序原理图报告讲解视频) 仿真图proteus7.8及以上 程序编译器&#x…...

Spring Boot 配置文件加密
方式一:Spring Cloud Config 一、建立config server 1. build.gradle 文件中添加: plugins {id javaid org.springframework.boot version 2.7.0id io.spring.dependency-management version 1.0.11.RELEASE }ext {set(springCloudVersion, "202…...
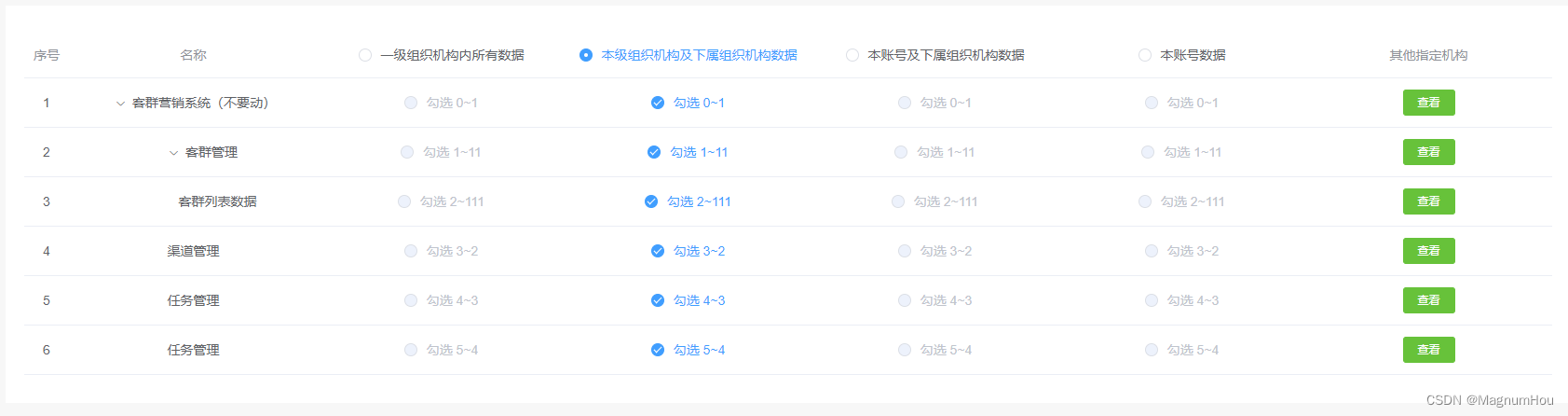
【树形权限】树形列表权限互斥选择、el-tree设置禁用等等
需求:按照权限管理配置的数据权限树展开;点击查看按钮后进入其他指定机构选择弹窗为一树形结构 本文章对项目中出现得关键点进行总结。 一、实现如上树形列表 在 element 官方表格示例中,实现树形表格列表数据渲染,非常简单。只…...
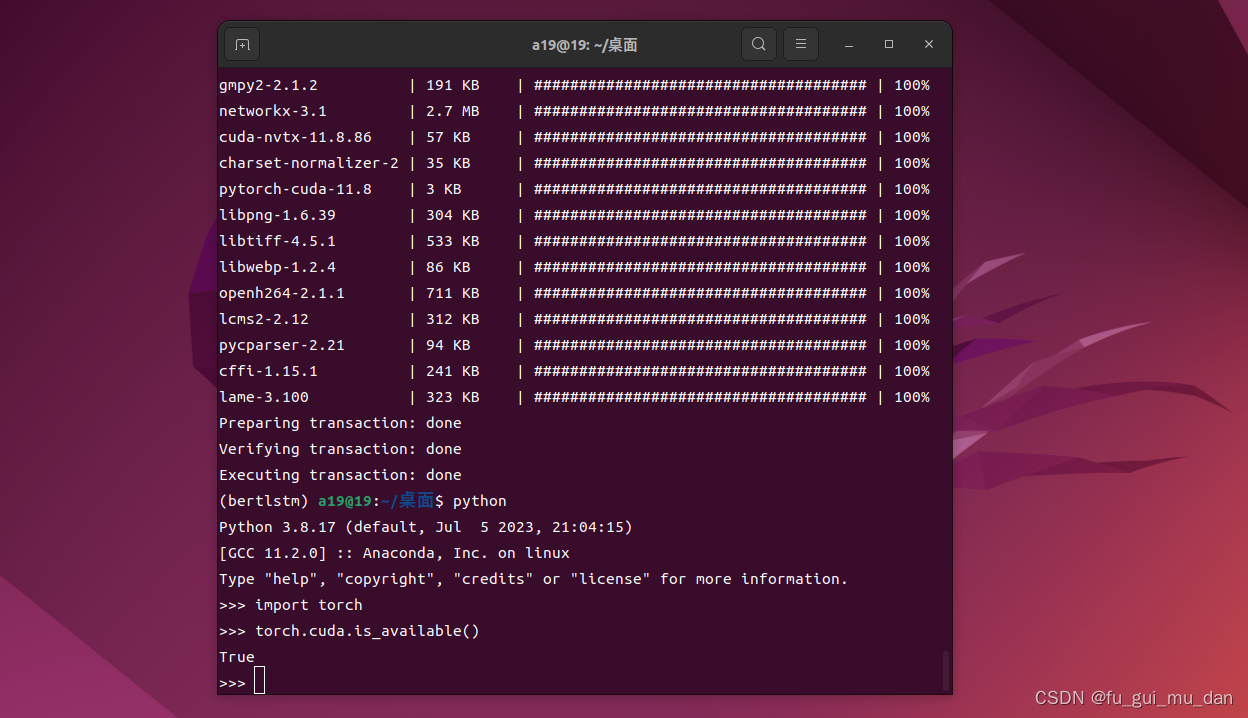
ubuntu 22.04安装cuda、cudnn、conda、pytorch
1、cuda 视频连接 https://www.bilibili.com/video/BV1bW4y197Mo/?spm_id_from333.999.0.0&vd_source3b42b36e44d271f58e90f86679d77db7cuda 11.8 https://developer.nvidia.com/cuda-toolkit-archive点击进入 https://developer.nvidia.com/cuda-11-8-0-download-arc…...

2023 最新前端面试题 (HTML 篇)
1. src 和 href 的区别 src 用于替换当前元素(引入),href 用于在当前文档和引用资源之间确立联系(引用) (1)src(source) 指向外部资源的位置,指向的内容将会嵌…...
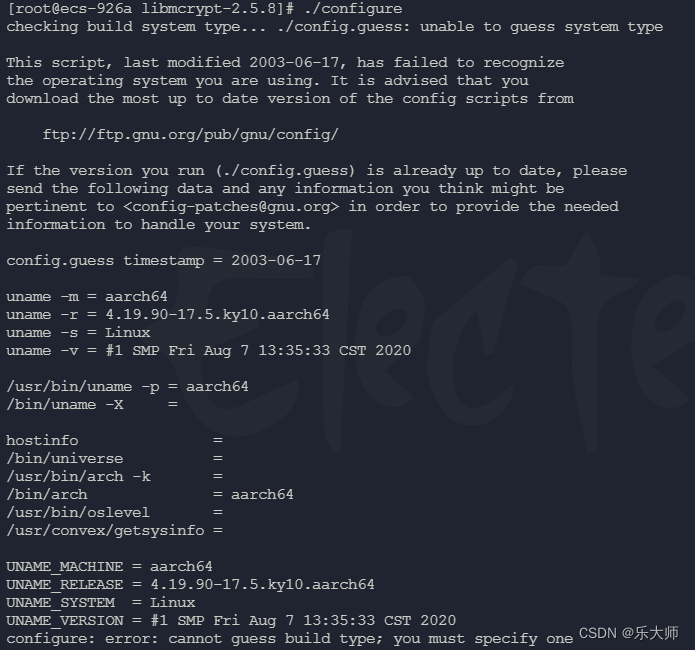
华为云银河麒麟V10安装libmcrypt
本次安装是在华为云上执行。cpu是鲲鹏,操作系统是银河麒麟V10. 先下载安装包: wget http://downloads.sourceforge.net/mcrypt/libmcrypt-2.5.8.tar.gz 解包,进入目录中。 执行如下命令: ./configure make make install 执…...

智慧导览|智能导游系统|AR景区导览系统|景区电子导览
随着文旅市场的加快复苏,以及元宇宙、VR、AR、虚拟数字人等新兴技术的快速发展,文旅行业也正在加快数字化转型的步伐,向智慧景区建设迈进。为满足不同年龄段游客的游览需要,提升旅游服务体验,越来越多的旅游景区、博物…...

【Docker】Docker基本使用介绍
Docker是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux机器上,也可以实现虚拟化。 一、安装Docker 首先,你需要从官方网站上下载Docker的安装包,并按…...

Linux命令200例:man用于显示和阅读关于Linux内置命令的使用说明
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌。CSDN专家博主,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师࿰…...
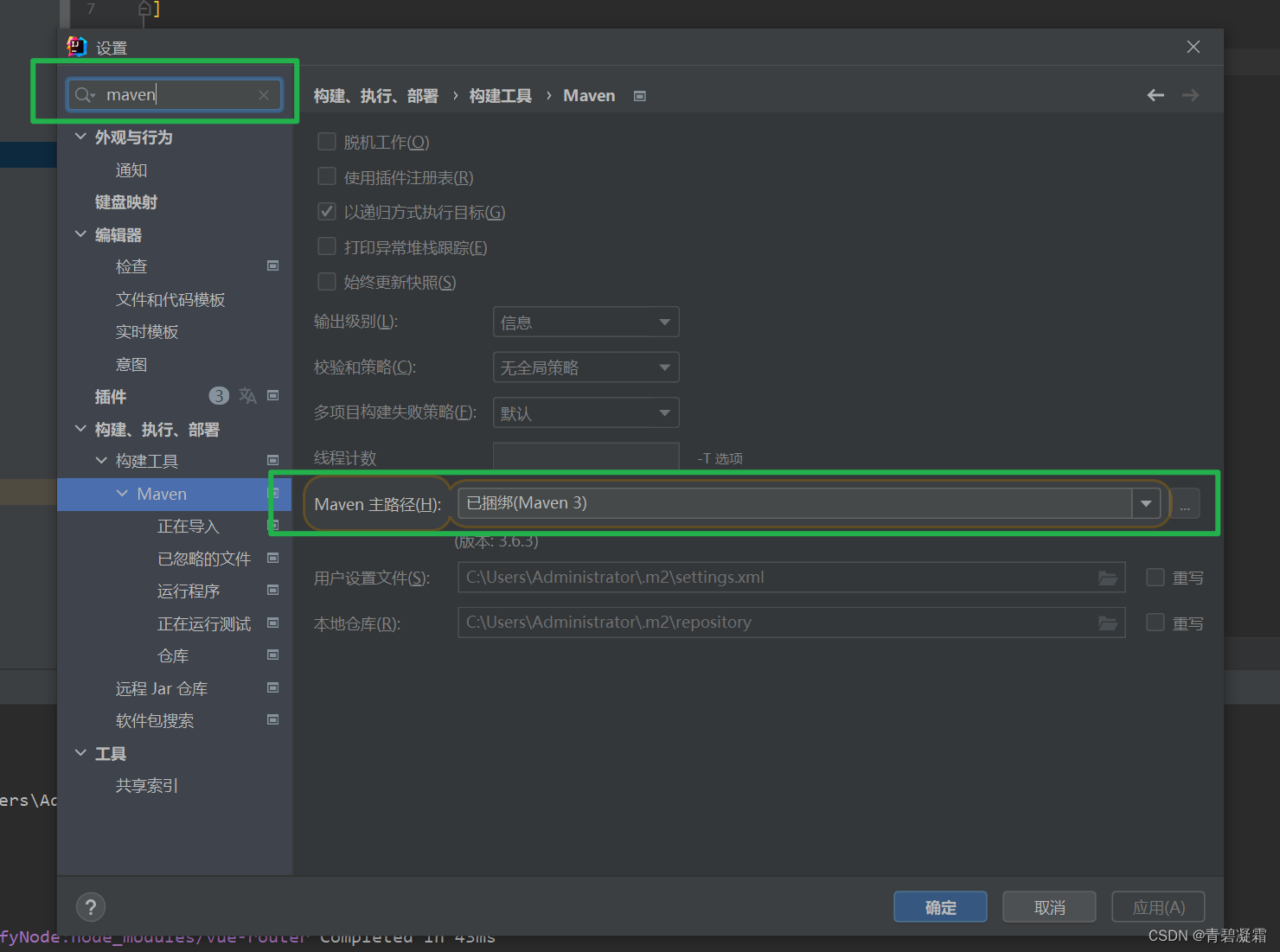
idea 无法识别maven的解决
问题描述 从git拉取代码或者修改文件夹以后,整个项目所有依赖爆红无法通过修改或者重新加载maven解决版本为idea 2021 问题定位 maven的版本太高,而idea的般本太低,导致识别的时候稳定性差 解决 使用idea原生的maven版本 选择已捆绑的m…...

String底层函数的实现方式
一、常见的String封装函数 1. strcpy函数的实现 char *strcpy(char *dest, const char *src) {char *tmp dest;while ((*dest *src) ! \0)/* nothing */;return tmp; } 2. strncpy函数的实现 char *strncpy(char *dest, const char *src, size_t count) {char *tmp dest…...

uniapp实现微信小程序全局可分享功能
uniapp实现微信小程序全局【发送给朋友】、【分享到朋友圈】、【复制链接】 主要使用 Vue.js 的 全局混入 1.创建一个全局分享的js文件。示例文件路径为:./utils/shareWx.js ,在该文件中定义全局分享的内容: export default {data() {retur…...

大数据成为市场营销利器 ,促进金融贷款企业获客精准化
随着大数据技术的不断普及,中国对尖端技术和云计算技术的投资大幅增加。大数据、云计算技术、物联网等一系列新一代信息技术也加速完善。 目前,大数据技术也非常成熟,大数据的应用领域也多种多样。大数据的重要方面“运营商大数据”已经被政…...

Acwing 3472. 八皇后
题目如下: 会下国际象棋的人都很清楚:皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。 如何将 88 个皇后放在棋盘上(有 88 个方格),使它们谁也不能被吃掉! 这就是著名的八皇后问题。 对于某个满足要…...

Word转为PDF后图片模糊怎么办?Word转为PDF的技巧介绍
将Word文档转为PDF是我们日常办公和文档处理中常见的需求。PDF格式的优势在于跨平台兼容性、保留原始格式、文档保护以及方便共享和分发等方面。本文将探讨Word转为PDF后图片模糊怎么办?Word转为PDF的技巧有哪些?通过这些问题的答案,可以帮助您更好的利用文件转换…...
【django开发手册】详解drf filter中DjangoFilterBackend,SearchFilter,OrderingFilter使用方式
💖 作者简介:大家好,我是Zeeland,开源建设者与全栈领域优质创作者。📝 CSDN主页:Zeeland🔥📣 我的博客:Zeeland📚 Github主页: Undertone0809 (Zeeland)&…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
