【力扣周赛】第 360 场周赛(贪心 ⭐树上倍增)
文章目录
- 竞赛链接
- Q1:8015. 距离原点最远的点(贪心)
- Q2:8022. 找出美丽数组的最小和(贪心)
- Q3:2835. 使子序列的和等于目标的最少操作次数(贪心)
- 思路
- 竞赛时丑陋代码(有一说一没眼看,现在已经忘了当时是怎么想的了)
- 优雅代码
- Q4:2836. 在传球游戏中最大化函数值(⭐⭐⭐⭐⭐树上倍增)
- 解法——利用倍增算法
- 模板题——1483. 树节点的第 K 个祖先
- 成绩记录
竞赛链接
https://leetcode.cn/contest/weekly-contest-360
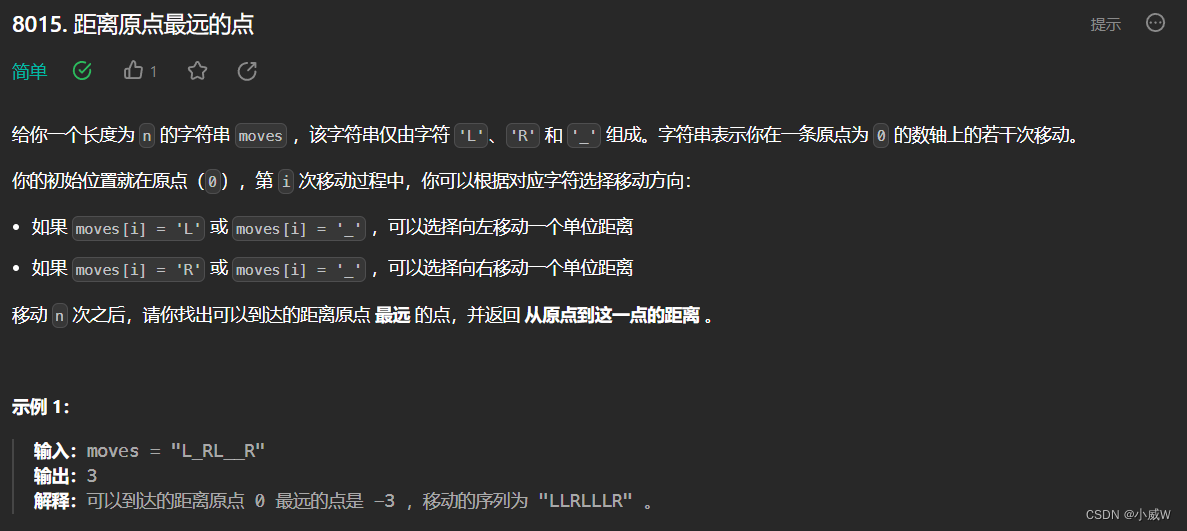
Q1:8015. 距离原点最远的点(贪心)
https://leetcode.cn/problems/furthest-point-from-origin/
提示:
1 <= moves.length == n <= 50
moves 仅由字符 'L'、'R' 和 '_' 组成
抓住本质,R 和 L 是不能改变的,而 _ 是可以随意选择的,因此可以在最后决定 _ 往哪个方向走。
class Solution {public int furthestDistanceFromOrigin(String moves) {int ans = 0, cnt = 0, pos = 0;for (char ch: moves.toCharArray()) {if (ch == 'R') pos++;else if (ch == 'L') pos--;else cnt++;}return Math.abs(pos) + cnt;}
}
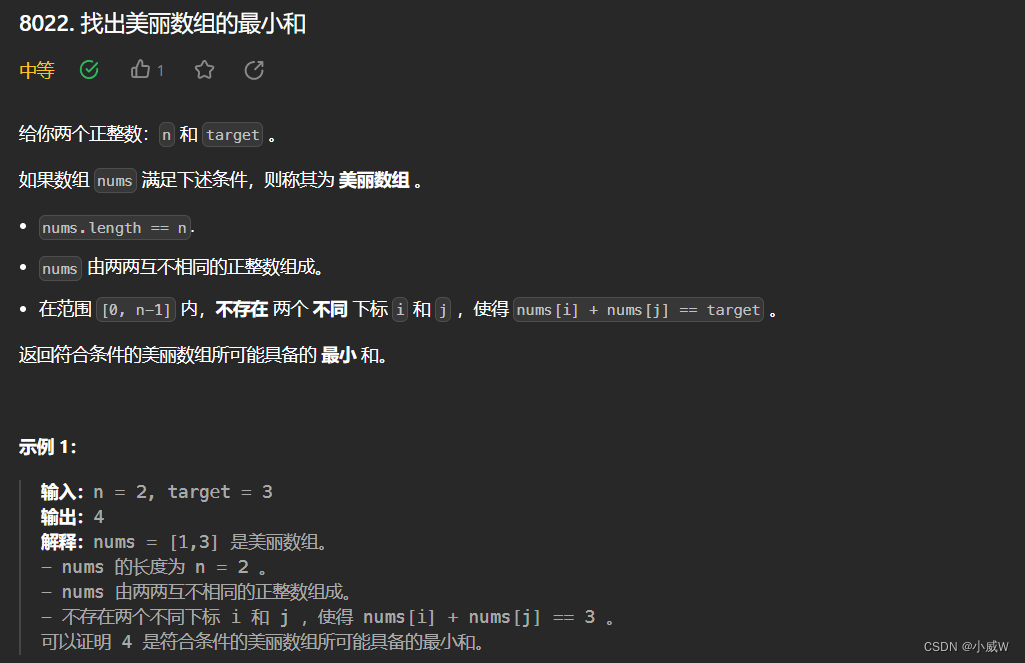
Q2:8022. 找出美丽数组的最小和(贪心)
https://leetcode.cn/problems/find-the-minimum-possible-sum-of-a-beautiful-array/
提示:
1 <= n <= 10^5
1 <= target <= 10^5
这道题目和 第 359 场周赛 中的 6450. k-avoiding 数组的最小总和 几乎一样。
我们还是用贪心来解决,从小到大,能选就选。
class Solution {public long minimumPossibleSum(int n, int target) {long ans = 0;Set<Integer> s = new HashSet<>();for (int i = 1; s.size() < n; ++i) {if (!s.contains(target - i)) {s.add(i);ans += i;}}return ans;}
}
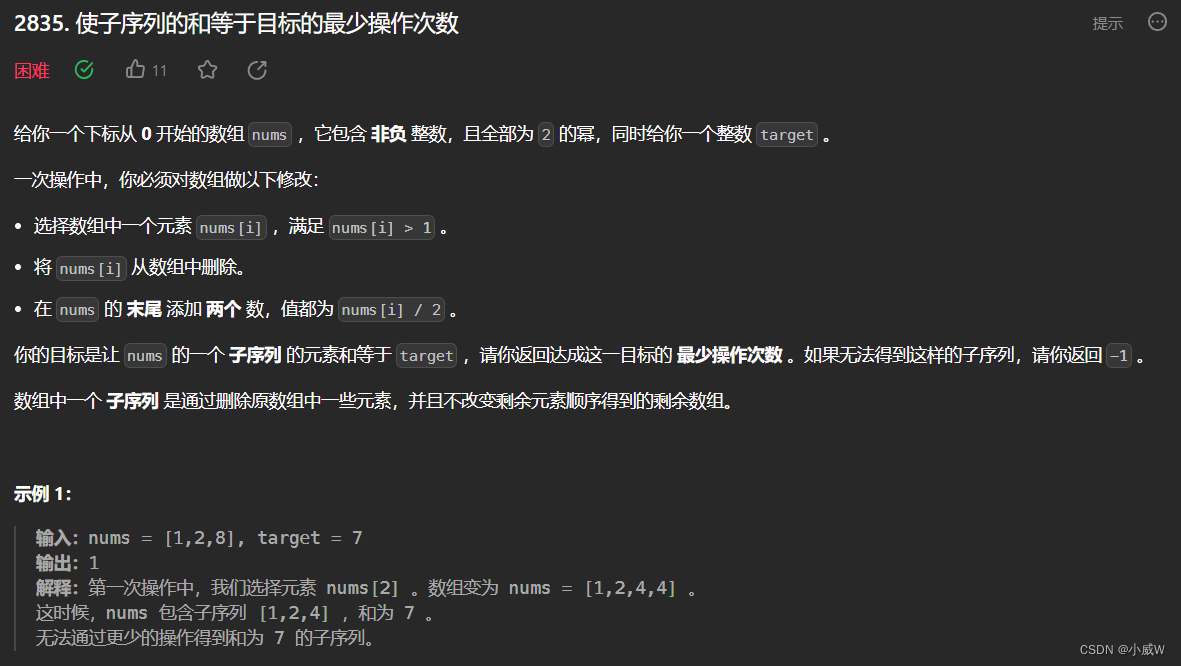
Q3:2835. 使子序列的和等于目标的最少操作次数(贪心)
https://leetcode.cn/problems/minimum-operations-to-form-subsequence-with-target-sum/
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 2^30
nums 只包含非负整数,且均为 2 的幂。
1 <= target < 2^31
思路
首先确定 sum >= target 则一定有解,否则一定无解。

竞赛时丑陋代码(有一说一没眼看,现在已经忘了当时是怎么想的了)
class Solution {static Map<Integer, Integer> m = new HashMap(), m2 = new HashMap();static {for (int i = 0, v = 1; i <= 30; ++i, v *= 2) {m.put(v, i);m2.put(i, v);}}public int minOperations(List<Integer> nums, int target) {long sum = 0;int[] cnt = new int[31], cnt2 = new int[31];for (int num: nums) {sum += num;cnt[m.get(num)]++;}if (sum < target) return -1;for (int i = 30; i >= 0; --i) {if (target >= m2.get(i)) {cnt2[i]++;target -= m2.get(i);}}int v = 0, ans = 0, last = -1;for (int i = 0; i <= 30; ++i) {if (cnt[i] > cnt2[i]) {if (last != -1) {ans += i - last;last = -1;v += (cnt[i] - cnt2[i] - 1) * m2.get(i);} else {v += (cnt[i] - cnt2[i]) * m2.get(i);}} else if (cnt[i] < cnt2[i]) {if (v >= (cnt2[i] - cnt[i]) * m2.get(i)) {v -= (cnt2[i] - cnt[i]) * m2.get(i);}else if (last == -1) last = i;}}return ans;}
}
优雅代码
https://leetcode.cn/problems/minimum-operations-to-form-subsequence-with-target-sum/solutions/2413344/tan-xin-by-endlesscheng-immn/
class Solution {public int minOperations(List<Integer> nums, int target) {long s = 0; // 求和long[] cnt = new long[31]; // 统计2^i的数量for (int x: nums) {s += x;cnt[Integer.numberOfTrailingZeros(x)]++;}if (s < target) return -1; // 无解的情况int ans = 0, i = 0;s = 0;// 注意这里是1L,因为i 最大是 30,这是可以进循环的,但是加一后就变成 31 了,虽然一定不会进入循环,但是要在 while 那里判断一下。while ((1L << i) <= target) {s += cnt[i] << i;int mask = (int) ((1L << ++i) - 1);if (s >= (target & mask)) continue; // 检查当前和能否填补target部分ans++; // 否则需要分解更大的数字while (cnt[i] == 0) {ans++;i++;}}return ans;}
}
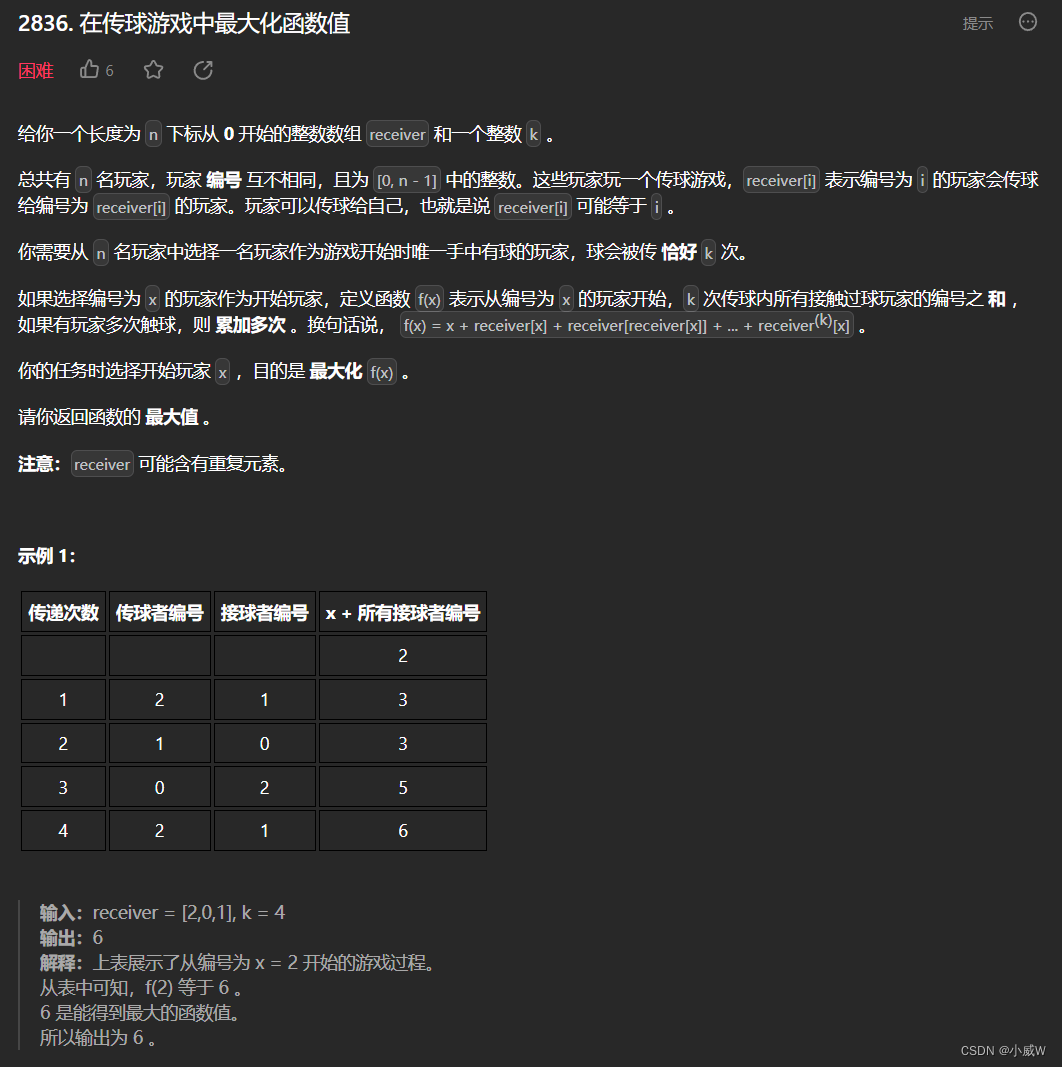
Q4:2836. 在传球游戏中最大化函数值(⭐⭐⭐⭐⭐树上倍增)
https://leetcode.cn/problems/maximize-value-of-function-in-a-ball-passing-game/
提示:
1 <= receiver.length == n <= 10^5
0 <= receiver[i] <= n - 1
1 <= k <= 10^10
解法——利用倍增算法
利用倍增算法,预处理每个节点 x 的第 2^i个祖先节点,以及从 x 的父节点到 x 的第 2^i 个祖先节点的节点编号之和。最后枚举起点 x,一边向上跳一边累加节点编号。
可以从代码模板中修改过来,多了要维护节点之间的和。
class Solution {public long getMaxFunctionValue(List<Integer> receiver, long k) {int n = receiver.size(); // 节点的个数int m = 64 - Long.numberOfLeadingZeros(k); // k的二进制长度int[][] pa = new int[n][m]; // 节点x的第2^i个祖宗节点的变好long[][] sum = new long[n][m]; // 节点x的父节点到x的第2^i个祖宗节点的节点编号之和// 初始化dp数组for (int i = 0; i < n; ++i) {pa[i][0] = receiver.get(i);sum[i][0] = receiver.get(i);}// 递推dp数组(先枚举i,再枚举x)for (int i = 0; i < m - 1; ++i) { // 注意这里的条件是 i < m - 1for (int x = 0; x < n; ++x) {int p = pa[x][i];pa[x][i + 1] = p < 0? -1: pa[p][i];// 合并节点的和 sum[x][i + 1] = sum[x][i] + sum[p][i]; }}long ans = 0;// 枚举各个节点作为起始节点for (int i = 0; i < n; ++i) {long s = i;int x = i;for (long t = k; t > 0; t &= t - 1) {int ctz = Long.numberOfTrailingZeros(t);// 要先处理求和,再处理节点的变化s += sum[x][ctz]; x = pa[x][ctz];}ans = Math.max(ans, s);}return ans;}
}
受 cpu 缓存的影响,倍增的二维数组开成 log*n 会比 n*log 快很多。
二维数组开成 logn * n 的形状会比开成 n * logn 的形状快很多,是因为在计算机中,连续的内存访问比随机的内存访问更快。当我们按行访问一个二维数组时,我们可以利用缓存行的概念,即将一行的数据读入缓存中,这样下一次访问时就可以直接从缓存中读取数据,而不需要再次从内存中读取。如果我们按列访问二维数组,则每次访问都需要跨越多个缓存行,这样会导致缓存失效,从而降低程序的性能。因此,将二维数组按行存储可以提高程序的性能。
所以可以将代码修改成如下:
class Solution {public long getMaxFunctionValue(List<Integer> receiver, long k) {int n = receiver.size(); // 节点的个数int m = 64 - Long.numberOfLeadingZeros(k); // k的二进制长度int[][] pa = new int[m][n]; // 节点x的第2^i个祖宗节点的变好long[][] sum = new long[m][n]; // 节点x的父节点到x的第2^i个祖宗节点的节点编号之和// 初始化dp数组for (int i = 0; i < n; ++i) {pa[0][i] = receiver.get(i);sum[0][i] = receiver.get(i);}// 递推dp数组(先枚举i,再枚举x)for (int i = 0; i < m - 1; ++i) { // 注意这里的条件是 i < m - 1for (int x = 0; x < n; ++x) {int p = pa[i][x];pa[i + 1][x] = p < 0? -1: pa[i][p];// 合并节点的和 sum[i + 1][x] = sum[i][x] + sum[i][p]; }}long ans = 0;// 枚举各个节点作为起始节点for (int i = 0; i < n; ++i) {long s = i;int x = i;for (long t = k; t > 0; t &= t - 1) {int ctz = Long.numberOfTrailingZeros(t);// 要先处理求和,再处理节点的变化s += sum[ctz][x]; x = pa[ctz][x];}ans = Math.max(ans, s);}return ans;}
}
执行用时从 237ms 加速到了 65ms 。
模板题——1483. 树节点的第 K 个祖先
https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/description/

提示:
1 <= k <= n <= 5 * 10^4
parent[0] == -1 表示编号为 0 的节点是根节点。
对于所有的 0 < i < n ,0 <= parent[i] < n 总成立
0 <= node < n
至多查询 5 * 10^4 次
https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/solutions/2305895/mo-ban-jiang-jie-shu-shang-bei-zeng-suan-v3rw/

本质上是动态规划,记 pa[x][i] 为每个节点 x 的第 2^i 个祖先节点。(如果不存在则为 -1)。
计算方式如下:

pa[x][1] = pa[pa[x][0]][0] 的意思是,x 节点的爷爷是 x 节点的父亲的父亲。
一般的,有 pa[x][i + 1] = pa[pa[x][i]][i]。
class TreeAncestor {int[][] pa;// 使用原始数据将整个 pa 数组预处理出来public TreeAncestor(int n, int[] parent) {int m = 32 - Integer.numberOfLeadingZeros(n); // n的二进制长度pa = new int[n][m]; // 表示节点i的2^j个祖宗节点// 初始化dp数组,即填充每个节点的父亲节点for (int i = 0; i < n; ++i) {pa[i][0] = parent[i];}// 先枚举i,再枚举x// 相当于先算出所有爷爷节点,再算出所有爷爷的爷爷节点for (int i = 0; i < m - 1; i++) {for (int x = 0; x < n; ++x) {int p = pa[x][i]; // 取出x的第2^i个祖宗节点// x的第2^(i+1)个祖宗节点 等于 x的第2^i个祖宗节点的第2^i个祖宗节点pa[x][i + 1] = p < 0? -1: pa[p][i]; }}}// 取出node节点的第k个祖宗节点public int getKthAncestor(int node, int k) {// 写法1 从低位到高位枚举// int m = 32 - Integer.numberOfLeadingZeros(k); // k的二进制长度// for (int i = 0; i < m; ++i) {// if ((k >> i & 1) == 1) { // k的二进制当前位为1// node = pa[node][i];// if (node < 0) break;// }// }// return node;// 写法2 不断去掉k末尾的1for (; k != 0 && node != -1; k &= k - 1) {node = pa[node][Integer.numberOfTrailingZeros(k)];}return node;}
}/*** Your TreeAncestor object will be instantiated and called as such:* TreeAncestor obj = new TreeAncestor(n, parent);* int param_1 = obj.getKthAncestor(node,k);*/
成绩记录

最后一题实在是写不出来了。(不过还好好像大家也都写不出来)
相关文章:

【力扣周赛】第 360 场周赛(贪心 ⭐树上倍增)
文章目录 竞赛链接Q1:8015. 距离原点最远的点(贪心)Q2:8022. 找出美丽数组的最小和(贪心)Q3:2835. 使子序列的和等于目标的最少操作次数(贪心)思路竞赛时丑陋代码&#x…...
企业如何防止数据外泄——【部署智能透明加密防泄密系统】
为防止公司文件泄密,可以采取以下措施: www.drhchina.com 分部门部署:根据不同的部门需要,为不同部门用户部署灵活的加密方案。例如,对研发部、销售部、运营部的机密资料进行强制性自动加密,对普通部门的文…...
【聚类】DBCAN聚类
OPTICS是基于DBSCAN改进的一种密度聚类算法,对参数不敏感。当需要用到基于密度的聚类算法时,可以作为DBSCAN的一种替代的优化方案,以实现更优的效果。 原理 基于密度的聚类算法(1)——DBSCAN详解_dbscan聚类_root-ca…...
通过安装cpolar内网穿透在Kali上实现SSH远程连接的步骤指南
文章目录 1. 启动kali ssh 服务2. kali 安装cpolar 内网穿透3. 配置kali ssh公网地址4. 远程连接5. 固定连接SSH公网地址6. SSH固定地址连接测试 简单几步通过cpolar 内网穿透软件实现ssh 远程连接kali! 1. 启动kali ssh 服务 默认新安装的kali系统会关闭ssh 连接服务,我们通…...
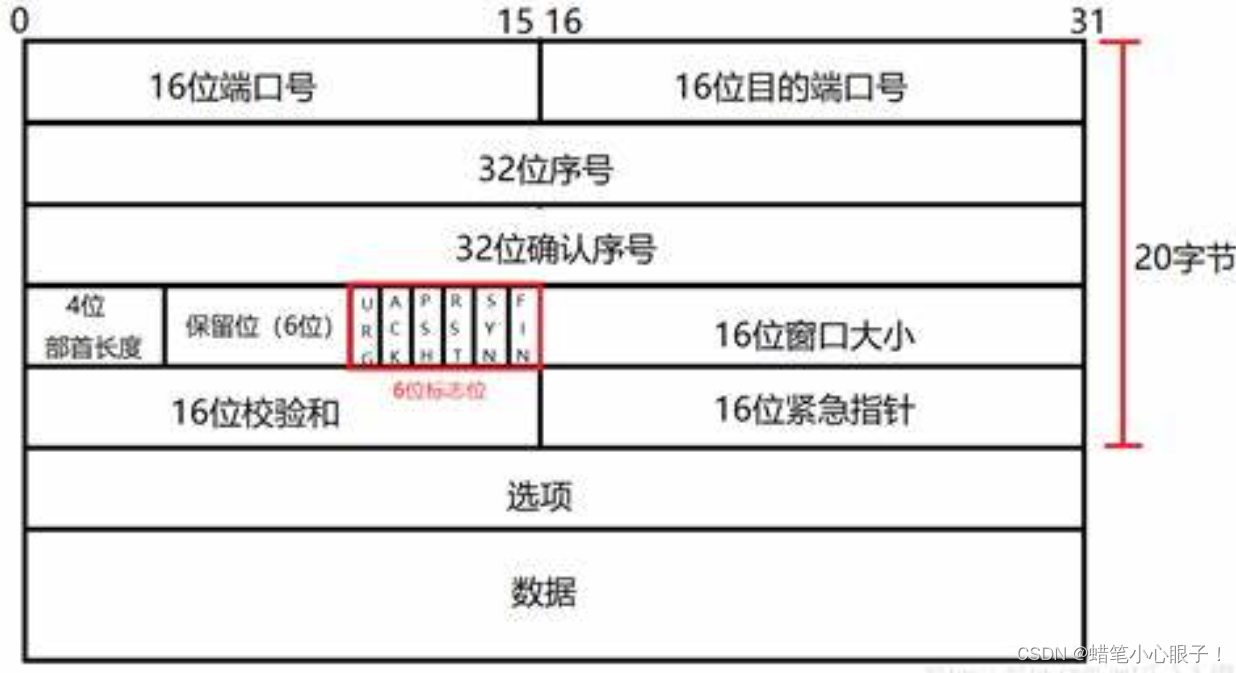
UDP和TCP协议报文格式详解
在初识网络原理(初识网络原理_蜡笔小心眼子!的博客-CSDN博客)这篇博客中,我们简单的了解了一下TCP/IP五层网络模型,这篇博客将详细的学习一下五层网络模型中传输层的两个著名协议:UDP和TCP 目录 一, 传输层的作用 二, UDP 1,UDP协议的特点 2,UDP报文格式 三, TC…...
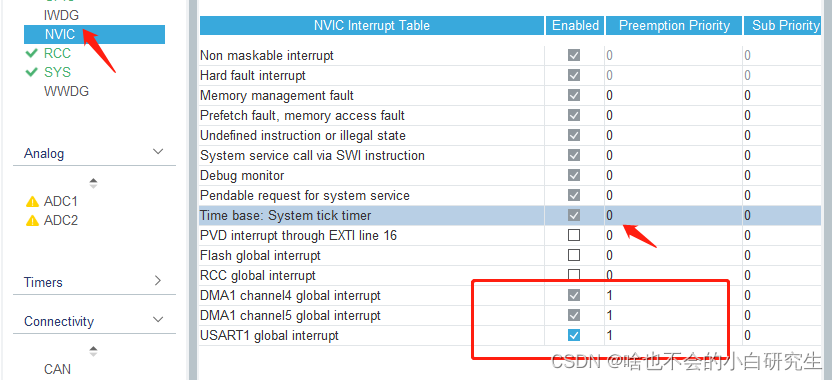
STM32+UART串口+DMA收发
目录 1、cubemax端配置 1.1 初始化配置 1.2 GPIO配置 1.3 UART配置 1.3.1 串口基础配置 1.3.2 DMA配置 2、keil端代码设计 2.1 初始化配置 2.2 DMA接收初始化配置 2.3 DMA发送配置 2.4 接收回调函数设置 2.5 回调函数内容代码编写 2.5.1 接收回调函数 2.5.2 发送回调…...

安全基础 --- js的闭包和this属性
js闭包 简介 一个函数和对其周围状态(lexical exviroment,词法环境)的引用捆绑在一起(或者说函数被引用包围),这样的组合就是闭包(closure) 在js中,通俗来讲,…...

【C语言每日一题】08. 字符三角形
题目来源:http://noi.openjudge.cn/ch0101/08 08 字符三角形 总时间限制: 1000ms 内存限制: 65536kB 问题描述 给定一个字符,用它构造一个底边长5个字符,高3个字符的等腰字符三角形。 输入 输入只有一行, 包含一个字符。 输出…...
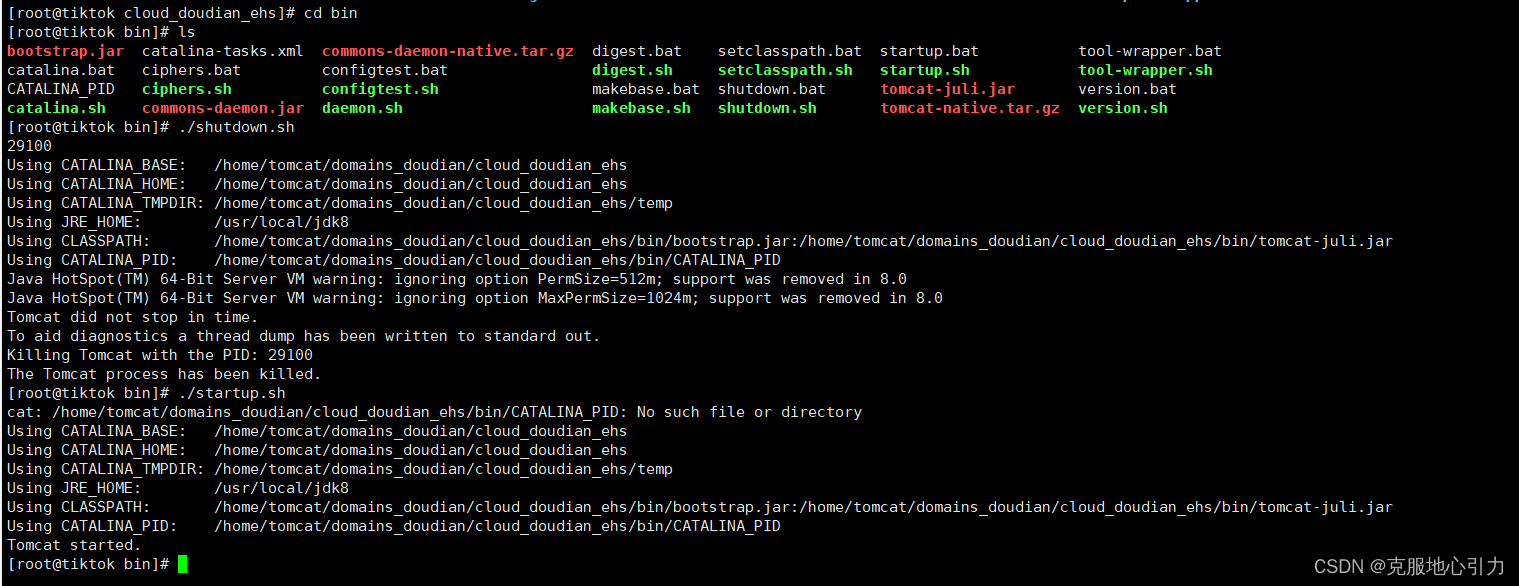
如何打war包,并用war包更新服务器版本
1.打包,我用的maven打包 先执行clean将已经生成的包清除掉 清除完,点package进行打包 控制台输出success,证明打包成功了 文件名.war的后缀就是生成的war包 2.将war包上传致服务器 一般会在war包加上日期版本上传至服务器 解压上传的war…...
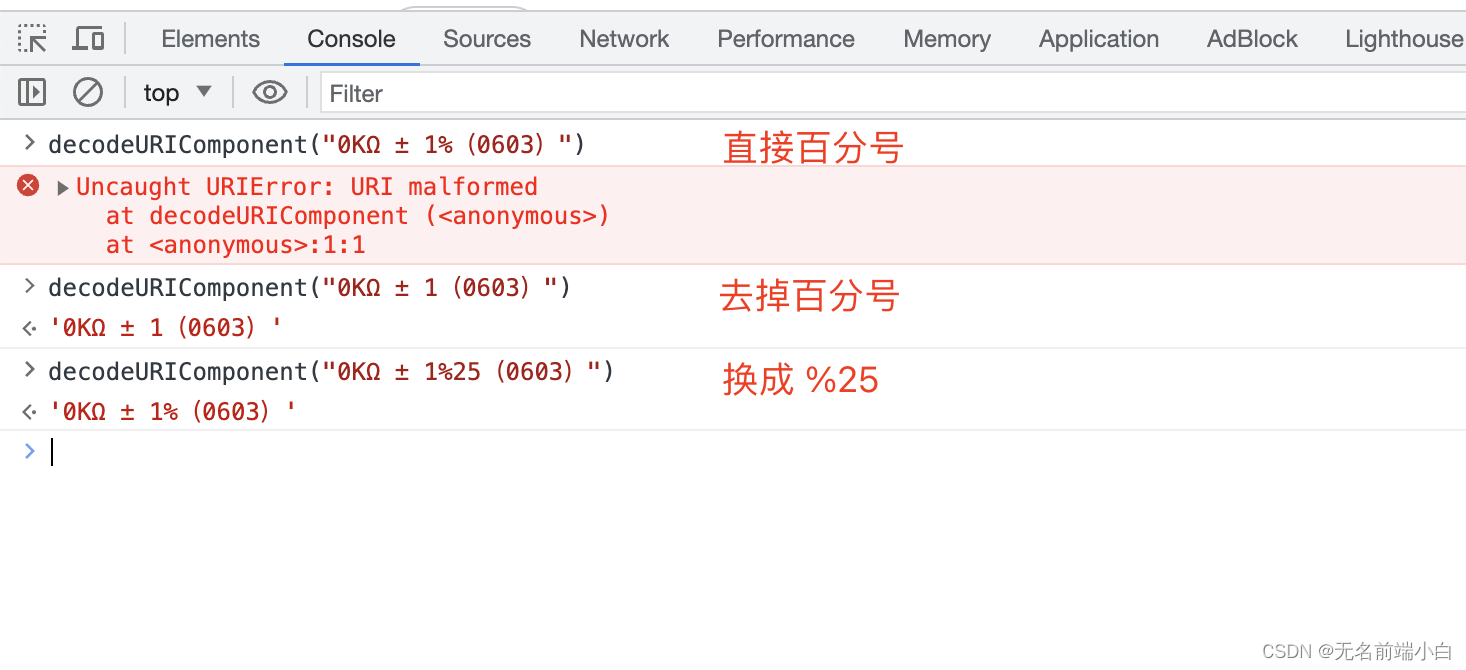
uniApp webview 中调用底座蓝牙打印功能异常
背景: 使用uniApp, 安卓底座 webView 方式开发; 调用方式采用H5 向 底座发送消息, 底座判断消息类型, 然后连接打印机进行打印; 内容通过指令集方式传递给打印机; 过程当中发现部分标签可以正常打印, 但又有部分不行,打印机没反应, 也没有报错; 原因分析: 对比标签内容…...

Mac下安装Jmeter及其配置
一、安装JDK环境 安装方式:mac下配置JDK环境_只看不学的博客-CSDN博客 如果已安装JDK环境即可忽略该步骤,检查方式,在终端输入java -version,如果出现了java版本,即代表已经配置过JDK环境了,如下图所示: …...

js+html实现打字游戏v1
实现逻辑:设置定时器每秒刷新一次,定时器刷新多少次执行一次生成单词操作来决定单词的生成速度,例如初始单词生成速度为1,那么定时器刷新5次才生成一次单词,每个单词用span来装,每组10个单词放到div里。监听…...

Java on VS Code 8月更新|反编译器用户体验优化、新 Maven 项目工作流、代码高亮稳定性提升
作者:Nick Zhu 排版:Alan Wang 大家好,欢迎来到 Visual Studio Code for Java 的 8 月更新!在这篇博客中,我们将为您提供有关反编译器支持的更多改进。此外,我们将展示如何创建没有原型的 Maven 项目以及一…...

划分Vlan时需要注意的问题
网络部分2019年才开始学习的,在学习过程中配置了整个公司的网络,心里才有了一点把握,算是掌握了最基本的。 不会的就上网学,反正网络上什么知识都有,只要有需求就对照着学,很长时间没有学习网络了ÿ…...

【广州华锐互动】利用AR远程指导系统进行机械故障排查,实现远程虚拟信息互动
随着工业自动化和智能化的不断发展,机械故障诊断已经成为了工业生产中的重要环节。为了提高故障诊断的准确性和效率,近年来,AR(增强现实)远程协助技术逐渐应用于机械故障诊断领域。本文将探讨AR远程协助技术在机械故障…...

Spring工具类--CollectionUtils的使用
原文网址:Spring工具类--CollectionUtils的使用_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Spring的CollectionUtils的使用。 CollectionUtils工具类的作用:操作Collection,比如:List、Set。 判断 方法作用static boolean is…...
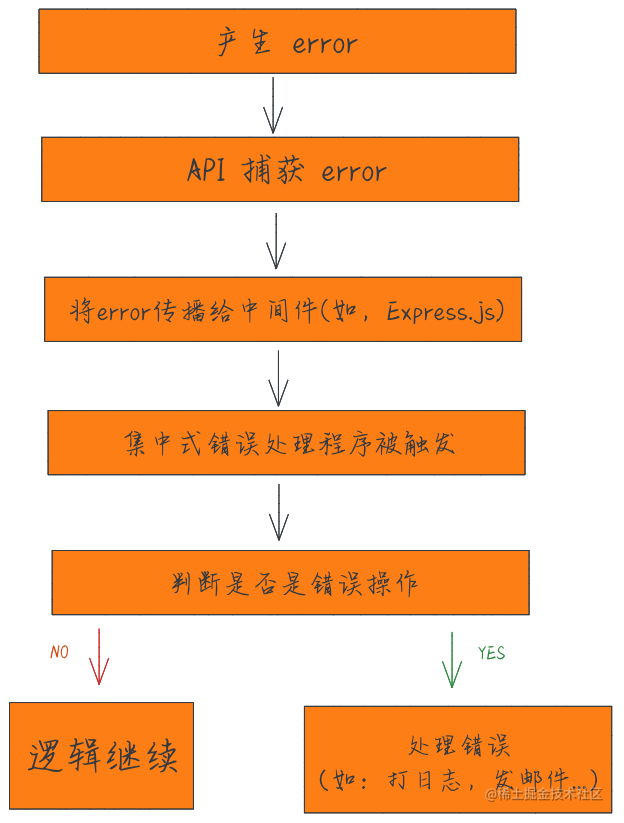
Node.js 应用的御用品: Node.js 错误处理系统
开发中,有些开发者会积极寻求处理错误,力求减少开发时间,但也有些人完全忽略了错误的存在。正确处理错误不仅意味着能够轻松发现和纠正错误,而且还意味着能够为大型应用程序开发出稳健的代码库。 特别是对于 Node.js 开发人员&am…...
K210-CanMV IDE开发软件
K210-CanMV IDE开发软件 界面功能简介连接设备临时运行开机运行程序 界面功能简介 区域①菜单栏:操作文件,使用工具等。 区域②快捷按钮:区域①中的文件和编辑中部分功能的快捷方式。 区域③连接设备:连接设备和程序控制按钮。 …...

0301yarnmapredude入门-hadoop-大数据学习
文章目录 1 MapReduce概述2 YARN2.1 yarn概述2.2 yarn与MapReduce关系2.3 yarn架构2.4 辅助角色 3 MapReduce & YARN部署3.1 集群规划3.2 配置文件3.3 分发配置文件 4 体验4.1 集群启动命令介绍4.2 提交MapReduce任务到YARN执行 结语 1 MapReduce概述 分布式计算是一种计算…...

大数据课程K15——Spark的TF-IDF计算Term权重
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解Spark的TF-IDF算法概念; ⚪ 了解Spark的TF-IDF算法定义; ⚪ 了解Spark的TF-IDF算法案例; 一、TF-IDF算法概述 TF-IDF(term frequency–inverse document frequency)是一种用于信…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...
