【动态规划】面试题 08.01. 三步问题

Halo,这里是Ppeua。平时主要更新C++,数据结构算法,Linux与ROS…感兴趣就关注我bua!
文章目录
- 0. 题目解析
- 1. 算法原理
- 1.1 状态表示
- 1.2 状态转移方程
- 1.3初始化
- 1.4 填表顺序
- 1.5 返回值
- 2.算法代码

🐧 本篇是整个动态规划的入门篇章,题目或许可以通过暴力或者其他方法求解但在这里,我们只讨论与动态规划相关的解法.
🐧 Gitee链接:面试题 08.01. 三步问题
0. 题目解析
题目链接:面试题 08.01. 三步问题
一个小孩一次能上1,2,3层阶梯,求解到n阶台阶时有多少种走法。
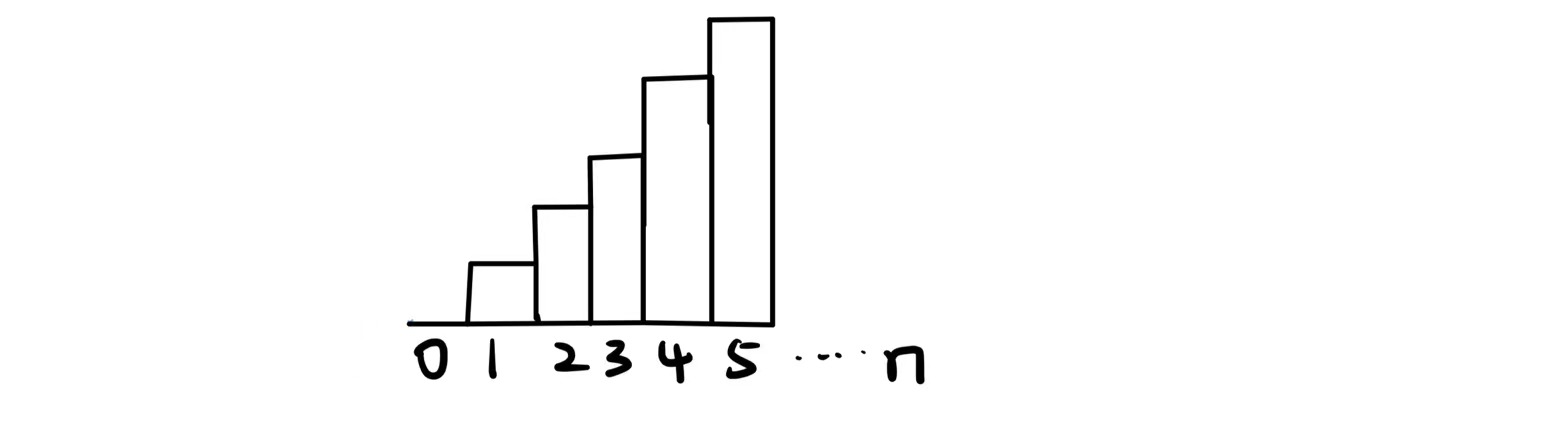
1. 算法原理
每个动态规划问题我们都会按照如下方法去分析.
1.1 状态表示
也就是dp数组(也称dp表)中,dp[i]所代表的意思是什么?
这个状态表示怎么来的?
-
分析题目的要求得出来的----按照这题为例 dp[i]等于 走到第n个台阶时所有的走法
-
根据以往做题的经验+题目的要求得出来的(这个我们之后会用到)
-
分析问题中发现重复的子问题 (较难的dp问题的状态表示往往由若干个子状态一起表示)
1.2 状态转移方程
这也就是如何求出dp[i]

我们观察发现,dp[i]可以由前三个台阶推出来.
例如:到台阶4的时候,可以由台阶一,台阶二,台阶三的步数走出来
具体的如下:可以由台阶1跳三格,台阶2跳两格,台阶3跳一格走到(注意这是一次跳的,而不是总共完成这么多格,所以只会有一种方法而不是多种)
所以如果我想要到台阶4的方法数就等于由台阶1的方法数+台阶2的方法数+台阶3的方法数.
所以dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
1.3初始化
核心思想为:保证数组不越界的情况下,完成我们的状态转移方程.
观察我们的状态转移方程,我们会发现,我们需要的值是i的前三个(i-1,i-2,i-3).所以当i=3时,最小位(i-3)此时为0.
这意味着:我们要保证不越界,我们的dp表要从i=3开始填,也就是i=0、1、2都已经初始化完
结合题目所给条件,我们不难发现:

所以初始化为:dp[0]=0,dp[1]=1,dp[2]=2
注意,当题目所给n的范围小于2时,我们访问dp[2]会造成越界.所以需要特判一下
1.4 填表顺序
为了保证填写当前状态的时候,所需要的状态已经计算过了,我们从左向右填
1.5 返回值
根据我们的dp[i]表示走到第i个台阶的方法数,而题目要求我们返回 走到第n个台阶的方法数,所以我们直接返回dp[n]即可
2.算法代码
class Solution {
int N=1000000007;
public:int waysToStep(int n) {vector<int>dp(n+1,0);if(n==1||n==2)return n;dp[0]=0,dp[1]=1,dp[2]=2,dp[3]=4;//o(n)时间复杂度 o(n)时间复杂度for(int i=4;i<=n;i++){dp[i]=((dp[i-1]%N+dp[i-2])%N+dp[i-3]%N)%N;}return dp[n];}
};
时间复杂度:o(n)
空间复杂度:o(n)
可以使用滚动数组的方法将空间复杂度优化到o(1)级别.
观察状态转移方程.我们发现,虽然我们开辟了n个大小的空间,但我们计算第i个的时候,只会用到前三个的值,这意味着在[0,i-4]这段区间中的数组空间都是浪费的.所以我们可以单独创建三个变量来表示所需要的状态值,来取代这个数组,从而优化空间复杂度.
空间,但我们计算第i个的时候,只会用到前三个的值,这意味着在[0,i-4]这段区间中的数组空间都是浪费的.所以我们可以单独创建三个变量来表示所需要的状态值,来取代这个数组,从而优化空间复杂度.
相关文章:

【动态规划】面试题 08.01. 三步问题
Halo,这里是Ppeua。平时主要更新C,数据结构算法,Linux与ROS…感兴趣就关注我bua! 文章目录 0. 题目解析1. 算法原理1.1 状态表示1.2 状态转移方程1.3初始化1.4 填表顺序1.5 返回值 2.算法代码 🐧 本篇是整个动态规划的…...

mac常见问题(三) macbook键盘溅上水怎么办?
多朋友在使用mac的时候难免会发生一些小意外,例如说本期要为大家说的macbook键盘溅上水或者其他的液体怎么办?不清楚的同学赶快get这项技能吧! 如果你不小心给你的MacBook键盘上溅了水或者其他液体,你需要超级快的把表面的液体清理…...

安全测试目录内容合集
基础知识 安全测试基础知识 安全测试-django防御安全策略 HTTP工作原理 靶场DVWA 安全测试网站-DWVA下载安装启动 DVWA-Command Injection DVWA-5.File upload 文件上传漏洞 DVWA-9.Weak Session IDs DVWA-XSS (Stored) DVWA-10.XSS (DOM)...

数据结构和算法(1):开始
算法概述 所谓算法,即特定计算模型下,旨在解决特定问题的指令序列 输入 待处理的信息(问题) 输出 经处理的信息(答案) 正确性 的确可以解决指定的问题 确定性 任一算法都可以描述为一个由基本操作组成的序…...

线下沙龙 | 从营销扩张到高效回款,游戏公司如何通过全链路运营实现高质量出海!
游戏出海,是近些年来中国产业的风暴出口,在2020至2023年期间保持着绝对的领航地位。公开数据显示,过去4年里,游戏在各类App出海份额中总体保持稳定,高达 64.9%。 但毕竟海外是陌生的市场,我们见过太多折戟沉…...
使用Jekyll + GitHub Pages搭建个人博客
本文将介绍如何使用Jekyll搭建个人博客,并部署在GitHub Pages上。 1.简介 Jekyll是一个强大的静态网站生成器,可以将Markdown、HTML、Liquid模板等文件转换为静态网站。Jekyll支持模板引擎、主题、插件、集成GitHub Pages等特性,可以帮助用…...
⽹络与HTTP 笔试题精讲1
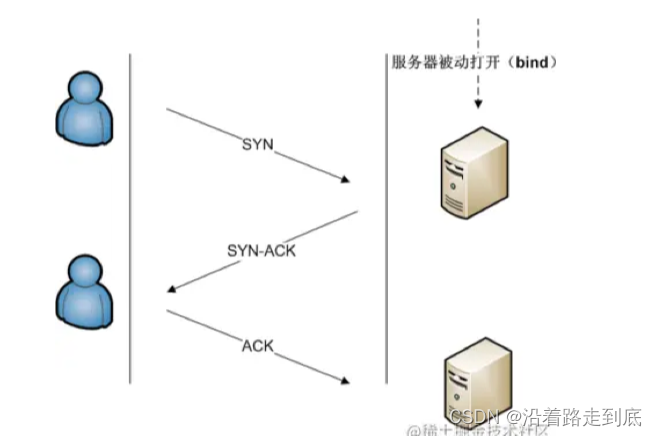
OSI七层与TCP/IP 这个就是OSI参考模型,⽽实际我们现在的互联⽹世界是就是这个理论模型的落地叫做TCP/IP协议 TCP的三次握⼿与四次挥⼿ 客户端想要发送数据给服务端,在发送实际的数据之前,需要先在两端之间建⽴连接,数据发完以后也需要将该连接关闭。建⽴连接的过程就是我们…...
亲测有效:虚拟机安装gcc,报错Could not retrieve mirrorlist http://mirrorlist.centos.org
(网卡配置资料) 原因: 网络问题 报错详情: One of the configured repositories failed (未知),and yum doesnt have enough cached data to continue. At this point the onlysafe thing yum can do is fail. There are a few …...

机器人中的数值优化(十二)——带约束优化问题简介、LP线性规划
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...

如何解决使用 ISPC 构建编译项目代码的时候出现_ISPCAlloc、_ISPCLaunch、_ISPCSync的连接器错误
一般在编译 ISPC 代码到时候,构建方法如下: $ ispc add.ispc -o add.o -h add.h $ g main.cpp add.o 但是在一些情况下连接器会报以下错误: $ g main.cpp add.o Undefined symbols for architecture x86_64:"_ISPCAlloc", refer…...
Hadoop 集群一直处于安全模式,强制退出后出现数据丢失警告。解决方法
文章目录 安全模式相关命令分析集群为什么一直处于安全模式解决方法 安全模式相关命令 # 查看安全模式状态 hdfs dfsadmin -safemode get# 进入安全模式 hdfs dfsadmin -safemode enter# 离开安全模式 hdfs dfsadmin -safemode leave# 强制退出安全模式 hdfs dfsadmin -safemo…...

四旋翼飞行器基本模型(MatlabSimulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
P1116 车厢重组(冒泡排序)
题目描述 在一个旧式的火车站旁边有一座桥,其桥面可以绕河中心的桥墩水平旋转。一个车站的职工发现桥的长度最多能容纳两节车厢,如果将桥旋转 180 180 180 度,则可以把相邻两节车厢的位置交换,用这种方法可以重新排列车厢的顺序…...
Android逆向学习(番外一)smali2java部分文件无法反编译的bug与修复方法
Android逆向学习(番外一)smali2java部分文件无法反编译的bug与修复方法 一、前言 昨天我和往常一样准备着android逆向(四)的博客,结果发现smali2java对某些文件无法进行逆向,我不知道windows会不会产生这…...
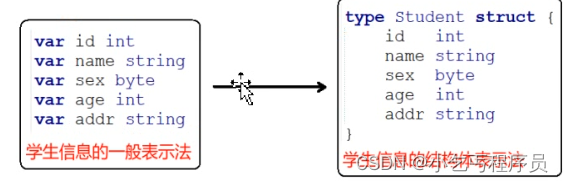
go语言基本操作---三
变量的内存和变量的地址 指针是一个代表着某个内存地址的值。这个内存地址往往是在内存中存储的另一个变量的值的起始位置。Go语言对指针的支持介于java语言和C/C语言之间,它即没有想Java语言那样取消了代码对指针的直接操作的能力,也避免了C/C语言中由…...

ArcGIS Enterprise + ArcGIS Pro 常用服务类型发布
发布前设置 门户连接 首先Pro需要先连接portal 添加portal门户地址,注意只到WA一级地址,并登录: 登录完成后,右键,设置为活动门户: 1. 发布动态地图服务 关联数据文件夹: 拖拽数据到地图…...

优思学院|亲和图案例:寻找六西格玛的项目
什么是亲和图? 亲和图(Affinity Diagram)主要功能在於分类归纳,协助在一堆杂乱无章的资料之中,有系统的归纳出几个大类,以利后续作业。通常先利用头脑风暴(Brainstorming)方式得到大…...

tomcat 的缓存机制
HTTP缓存:Tomcat支持HTTP缓存机制,可以通过设置响应头中的Cache-Control、Expires和ETag等字段来控制缓存策略。这些字段告诉浏览器是否可以缓存响应以及缓存的有效期等信息。 Servlet缓存:Tomcat还提供了Servlet缓存机制,它可以…...

laravel 压缩文件与解压文件
一、引入第三方类 composer require chumper/zipper二、第三方类配置 providers>[Chumper\Zipper\ZipperServiceProvider::class ]aliases > [Zipper > Chumper\Zipper\Zipper::class ]三、压缩解压缩实例 <?php namespace App\Http\Controllers\Upload; use A…...

kind搭建k8s集群用于测试
安装kind 需要先安装go kind基于go开发 #第一种安装方式#修改go源加快下载速度 go env -w GOPROXYhttps://goproxy.cn,direct #直接下载安装kind最新版本 go install sigs.k8s.io/kindlatest #进入GOPATH目录找到bin目录下kind执行程序 移动到环境变量里 mv ./kind /usr/local…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
