2605. 从两个数字数组里生成最小数字
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:枚举比较法
- 方法二:集合的位运算表示法
- 写在最后
Tag
【贪心】【位运算】【数组】
题目来源
2605. 从两个数字数组里生成最小数字

题目解读
给定两个各自只包含数字 1 到 9 的两个数组,每个数组中的元素互不相同,请你返回最小的数字,这个数字的数位至少包含两个数组中的数字。
解题思路
贪心的思想,如果两个数组有交集,则答案为交集中的最小值;否则,需要找出各个数组中的最小值,用最小值组成最小答案。
我们先来讲述最小值的计算,方法有很多,可以先升序排序(降序排序)再返回首位置元素(末位置元素),还可以直接使用 API *min_element() 来计算数组中的最小值。
计算两个数组的交集有以下两种方法:
- 枚举比较法。
- 集合的位运算表示法。
方法一:枚举比较法
枚举所有可能的数字组合,如果该组合中的两个数字一样,则加入到交集 section 中,如果集合 section 非空,则返回集合中的最小值。
实现代码
class Solution {
public:int minNumber(vector<int>& nums1, vector<int>& nums2) {vector<int> section;for (int i = 0; i < nums1.size(); ++i) {for (int j = 0; j < nums2.size(); ++j) {if (nums1[i] == nums2[j]) {section.push_back(nums1[i]);}}}if (!section.empty()) {return *min_element(section.begin(), section.end());}int min1 = *min_element(nums1.begin(), nums1.end());int min2 = *min_element(nums2.begin(), nums2.end());return min(min1 * 10 + min2, min2 * 10 + min1);}
};
复杂度分析
时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn), n n n 为最大的数组长度。
空间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)。
方法二:集合的位运算表示法
两个数组可以看作是两个集合,集合可以用二进制来表示,比如集合 S = { 1 , 2 , 3 } S = \{1, 2, 3\} S={1,2,3} 用二进制 1110 来表示,二进制数从右往左数的第 num 位为 1 表示数字 num 在集合中。
于是数组的交集就可以使用集合的交集来表示,交集可以用二进制的与操作计算,然后与操作得到的二进制数从右到左找到第一个 1 的位置,即为两个数组交集中的最小值,这里我们可以使用 __builtin_ctz() 来查找从右至左第一个 1 出现的位置。
关于集合用运算来表示,如果还有不明白的地方可以参考 位运算基础与应用 这篇文章。
实现代码
class Solution {
public:int minNumber(vector<int>& nums1, vector<int>& nums2) {// 位运算int mask1 = 0, mask2 = 0;for (int x : nums1) mask1 |= 1 << x;for (int x : nums2) mask2 |= 1 << x;int mask = mask1 & mask2;if (mask) return __builtin_ctz(mask);int x = __builtin_ctz(mask1), y = __builtin_ctz(mask2);return min(x * 10 + y, 10 * y + x);}
};
复杂度分析
时间复杂度: O ( n + m ) O(n+m) O(n+m),其中 n n n 为数组 nums1 的长度, m m m 为数组 nums2 的长度。
空间复杂度: O ( 1 ) O(1) O(1),仅使用了几个额外的变量。
写在最后
以上就是本篇文章的内容了,感谢您的阅读。🍗🍗🍗
如果感到有所收获的话可以给博主点一个 👍 哦。
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出。💬💬💬
相关文章:

2605. 从两个数字数组里生成最小数字
文章目录 Tag题目来源题目解读解题思路方法一:枚举比较法方法二:集合的位运算表示法 写在最后 Tag 【贪心】【位运算】【数组】 题目来源 2605. 从两个数字数组里生成最小数字 题目解读 给定两个各自只包含数字 1 到 9 的两个数组,每个数组…...
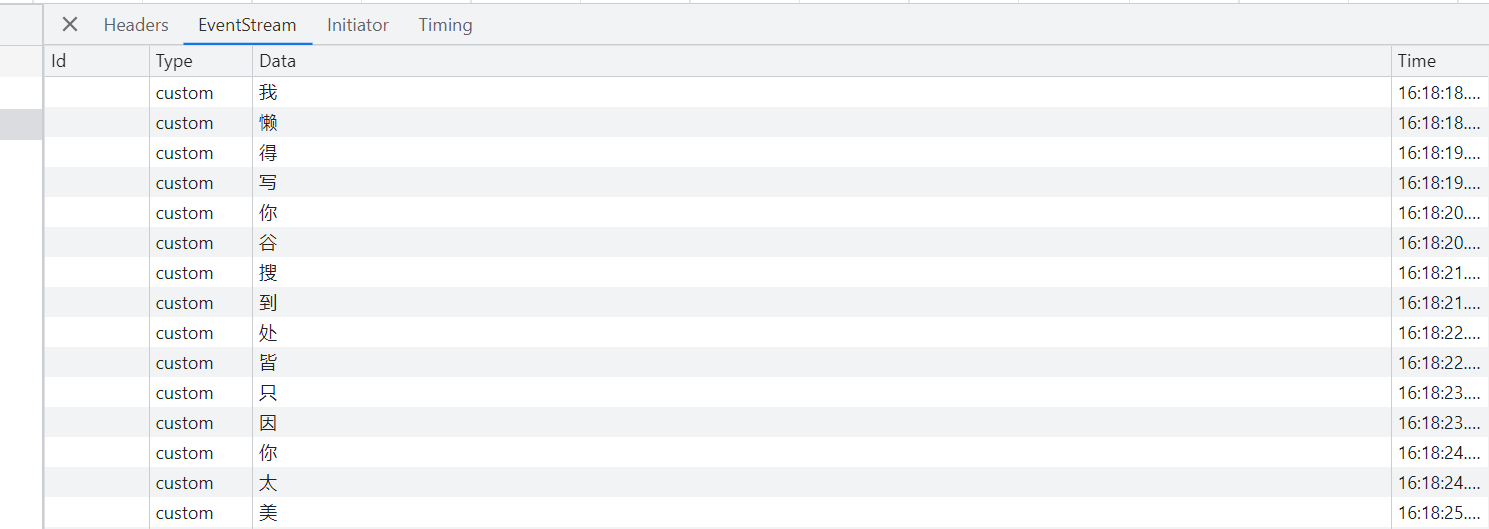
服务器发送事件Server-sent events详解与示例
Server-sent events 服务端进行数据推送除了WebSocket之外,还可以使用Server-Send-Event方案。 与 WebSocket不同的是,服务器发送事件是单向的。数据消息只能从服务端到发送到客户端(如用户的浏览器)。这使其成为不需要从客户端…...
SOLIDWORKS 多实体的建模方式
SOLIDWORKS多实体是SOLIDWORKS中一个非常有用的功能。在SOLIDWORKS中,对于模型的设定通常被大家所熟知的有以下几种类型:零件、装配体以及工程图。 其实还有一种划分,就是多实体。严格意义上来说,多实体既不属于零件也不属于装配体…...

NSSCTF web 刷题记录1
文章目录 前言题目[GXYCTF 2019]禁止套娃方法一方法二 [NCTF 2019]Fake XML cookbook[NSSRound#7 Team]ec_RCE[NCTF 2018]Flask PLUS 前言 今天是2023.9.3,大二开学前的最后一天。老实说ctf的功力还是不太够做的题目太少,新学期新气象。不可急于求成&am…...
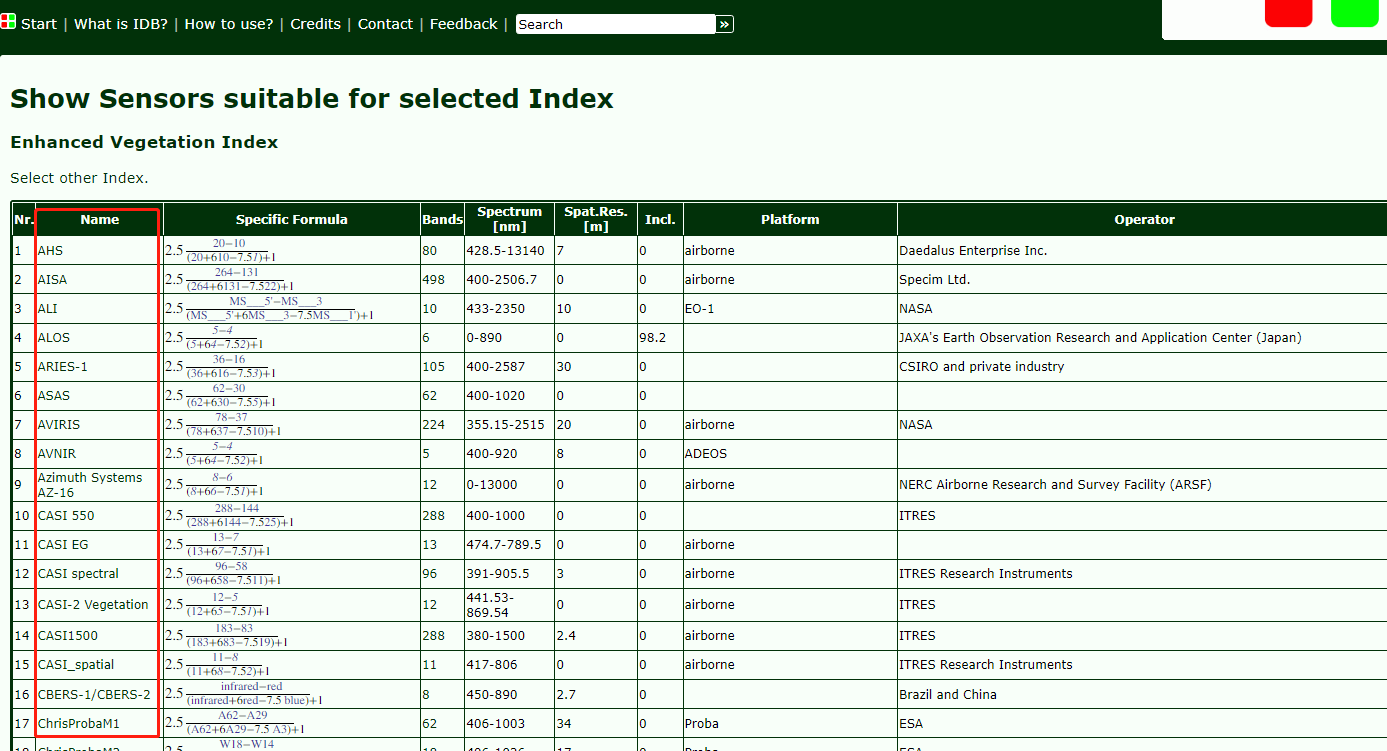
遥感指数数据库
目前遥感指数多种多样,那怎么针对不同的应用领域选择合适的植被指数?不同卫星又有哪些可以反演的指数? Henrich等人开发了Index Database(网址:https://www.indexdatabase.de/),总结了目前主流的遥感指数,…...
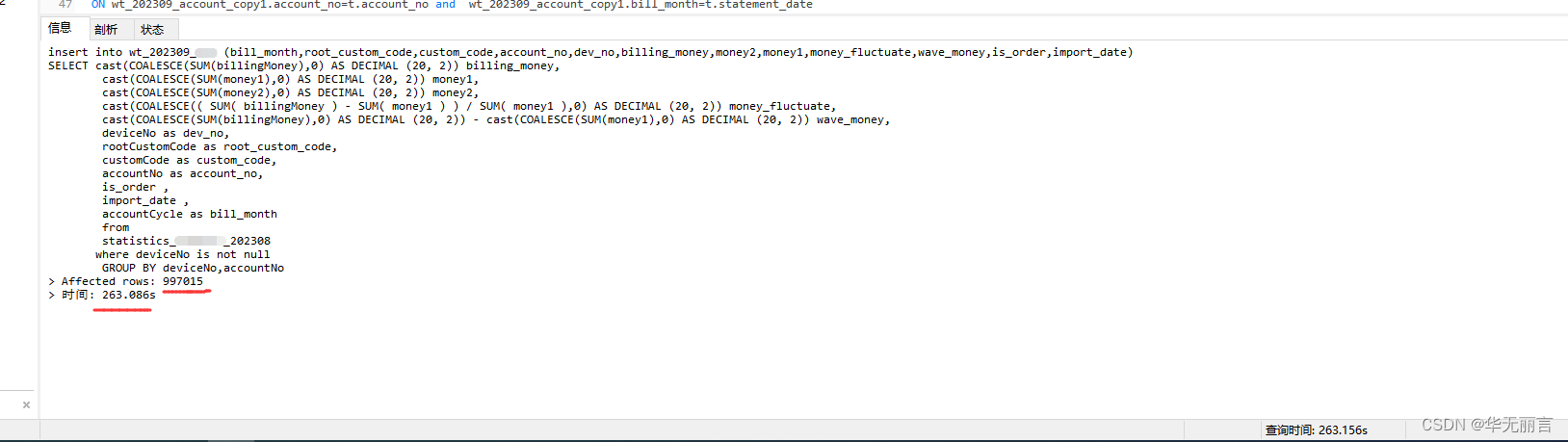
如何让insert程序速度快,可以试试联合SQL(insert 和 select 一起使用)?
查询添加可选择SQL执行,速度远超程序执行 insert 和 select案例 insert into 表1(列1,列2,列3,...) select 列1,列2,列3,...from表2(GROUP BY 列)116511 条数据 耗时45秒, 如果是程序查询然后再insert,则需要30分钟左右!&#x…...
IP地址、网关、网络/主机号、子网掩码关系
一、IP地址 IP地址组成 IP地址分为两个部分:网络号和主机号 (1)网络号:标识网段,保证相互连接的两个网段具有不同的标识。 (2)主机号:标识主机,同一网段内,主机之间具有相同的网…...

使用skvideo.io.vread读取avi视频,报错“No way to determine width or height from video...”
问题描述: 一开始安装sk-video,在使用skvideo.io.vread读取avi视频,报错“No way to determine width or height from video. Need -s in inputdict. Consult documentation on I/O.” 解决方案: 1. 卸载sk-video pip uninsta…...
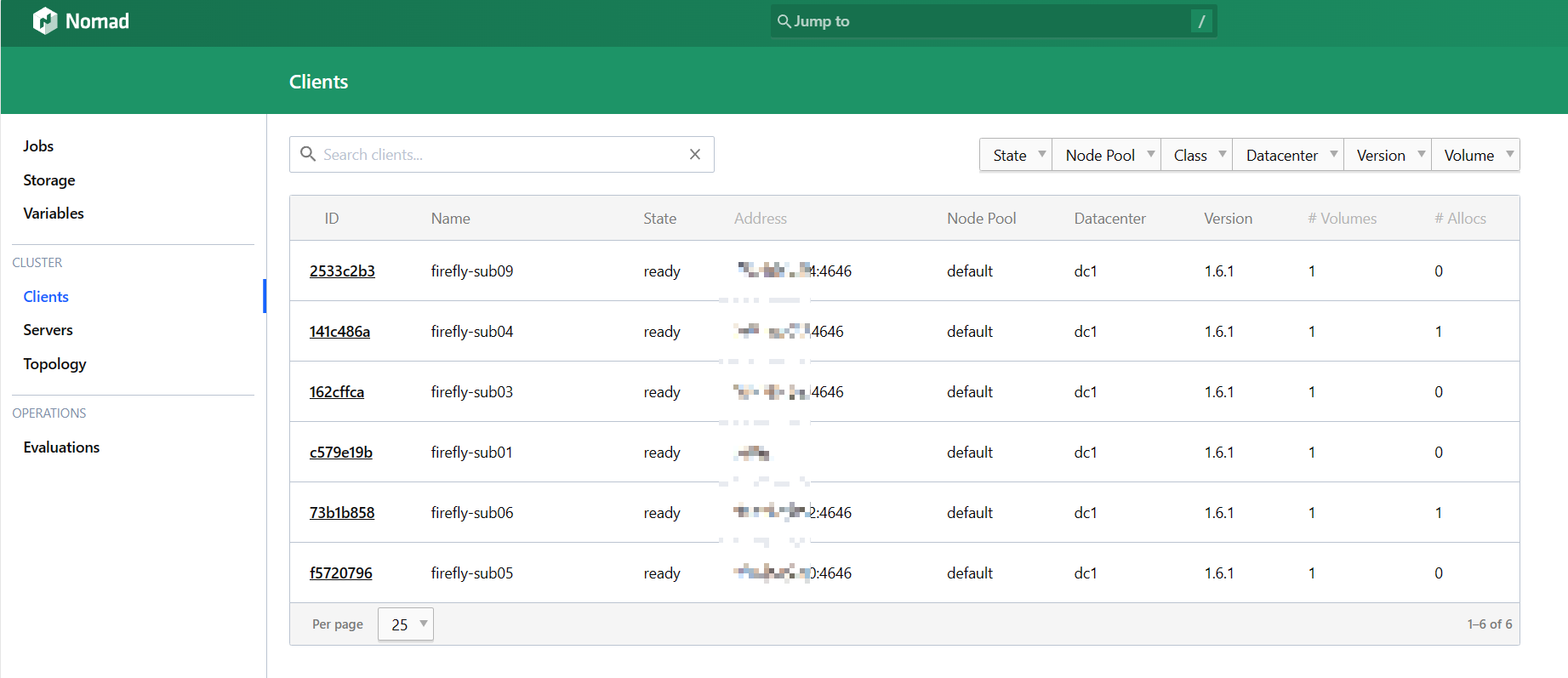
Nomad 系列-安装
系列文章 Nomad 系列文章 Nomad 简介 开新坑!近期算是把自己的家庭实验室环境初步搞好了,终于可以开始进入正题研究了。 首先开始的是 HashiCorp Nomad 系列,欢迎阅读。 关于 Nomad 的简介,之前在 大规模 IoT 边缘容器集群管…...
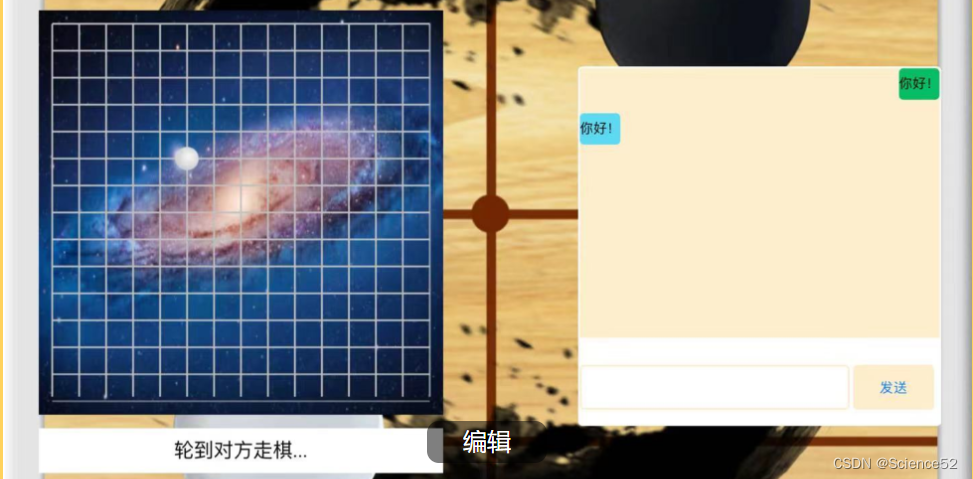
网络版五子棋C++实现
目录 1.项目介绍 2.开发环境 3.核心技术 4.环境搭建 5.WebSocketpp介绍 5.1WebSocketpp是什么 5.2为什么使用WebSocketpp 5.3原理解析: 5.4WebSocketpp主要特性 6.WebSocketpp使用 7.JsonCpp使用 8.MySQL API 9.项目模块设计以及流程图 10.封装日志宏…...

项目招标投标公众号小程序开源版开发
项目招标投标公众号小程序开源版开发 以下是一个招标投标公众号小程序的功能列表: 用户注册与登录:用户可以注册账号并登录公众号小程序。项目发布:用户可以发布招标项目的详细信息,包括项目名称、招标单位、项目描述、招标要求…...
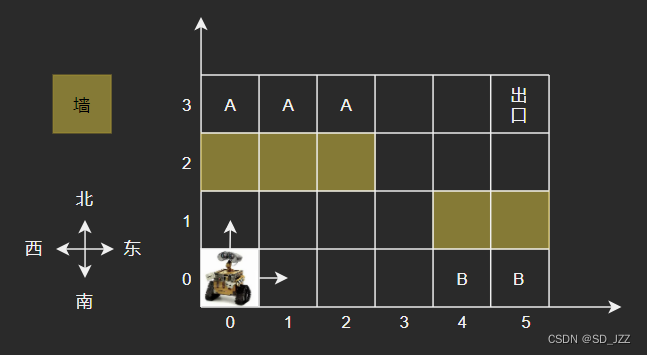
华为OD机试-机器人走迷宫
题目描述 机器人走一个迷宫,给出迷宫的x和y(x*y的迷宫)并且迷宫中有障碍物,输入k表示障碍物有k个,并且会将障碍物的坐标挨个输入. 机器人从0,0的位置走到x,y的位置并且只能向x,y增加的方向走,不能回退. 如代码类注释展示的样子,#表示可以走的方格,0代表障碍,机器人从0,0的位置…...

Jenkins搭建步骤Linux环境
1、进入目标目录开始准备环境 安装jdk 安装maven 安装tomcat 安装node 下载Jenkins.war并且拷贝进tomcat的webapp的文件夹下。 环境变量配置如下自行更改: #--------------For JDK---------------- export JAVA_HOME/usr/local/java/jdk1.8.0_192 export PATH/usr…...
2023 AZ900备考
文章目录 如何学习最近准备考AZ900考试,找了一圈文档,结果发现看那么多文档,不如直接看官方的教程https://learn.microsoft.com/zh-cn/certifications/exams/az-900/ ,简单直接,突然想到纳瓦尔宝典中提到多花时间进行思…...
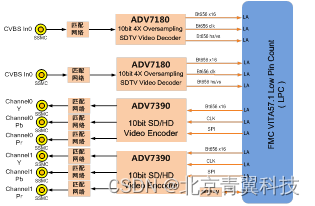
青翼科技基于VITA57.1的16路数据收发处理平台产品手册
FMC211是一款基于VITA57.1标准规范的实现16路LVDS数据采集、1路光纤数据收发处理FMC子卡模块。 该板卡支持2路CVBS(复合视频)视频输入,能够自动检测标准的模拟基带电视信号,并将其转变为8位ITU-R.656接口信号或者4:2:2分量视频信…...
)
Ansible_自动化运维实战(一)
1.DELL的一款服务器的价格、型号、配置(CPU,内存、硬盘、支持的RAID功能) DELL 服务器的定价、型号和配置因型号而异,可以通过访问 DELL 官方网站或联系 DELL 客户服务获取具体信息。一种示例是 DELL PowerEdge R740,其…...

说说Flink中的State
分析&回答 基本类型划分 在Flink中,按照基本类型,对State做了以下两类的划分: Keyed State,和Key有关的状态类型,它只能被基于KeyedStream之上的操作,方法所使用。我们可以从逻辑上理解这种状态是一…...

适合心理法律在线咨询预约含视频图文电话咨询功能的小程序开发
目前智能手机普及,很多以前需要线下咨询的场景都被搬到了线上,这样既可以使咨询者更方便,也可以使被咨询者接待效率更高,服务更多咨询者。基于此我们开发了专门的一款具有线上咨询功能的小程序,同时为了方便被咨询者服…...
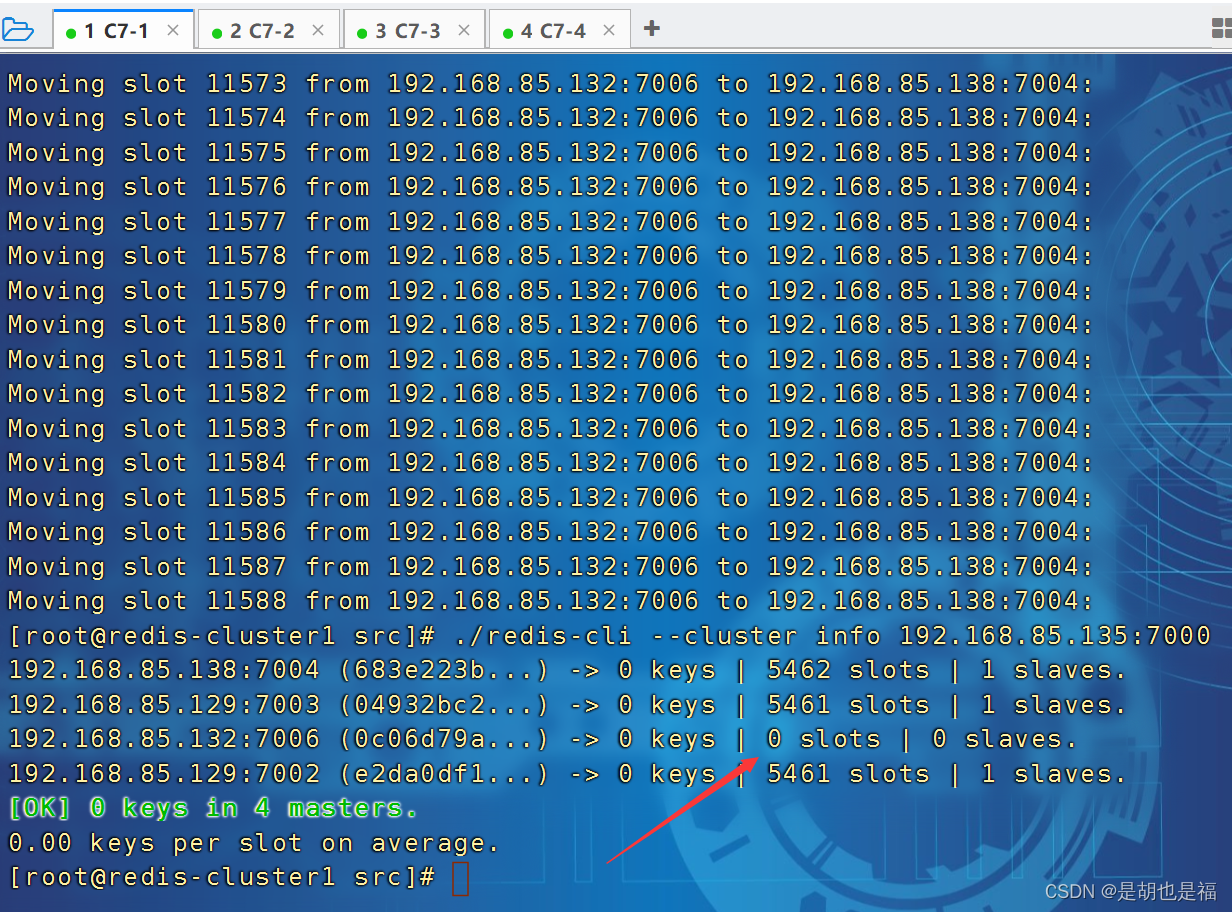
Redis-Cluster集群操作--添加节点、删除节点
一、环境部署 部署好Redis-Cluster集群,参考上个本人的博客:Redis-Cluster集群的部署(详细步骤)_是胡也是福的博客-CSDN博客 新准备一台机器,修改主机名,关闭防火墙和selinux,参考:…...

ModaHub魔搭社区:星环科技向量数据库Hippo社区版来啦
大语言模型正在与企业应用迅速结合,并深刻改变企业的各个产业环节。而大模型训练所使用的数据包含了如文档、图片、音视频等各种类型的非结构化数据,传统关系型数据库能力有限。通过将这些非结构化数据转换为多维向量,可以结构化地在向量数据库中进行管理,实现高效的数据存…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
