代码随想录算法训练营第三十八天 | ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
题目链接:509. 斐波那契数
代码随想录
视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili
看完代码随想录之后的想法:
我们要知道动态规划的五部曲;
1,确定dp数组的含义,下标的含义;
2,确定递推公式;
3,确定dp数组如何初始化;
4,确定遍历顺序;
5,打印dp数组(用来debug);
1这道题目dp数组是第i位斐波那契数的值,i是第i位
2,dp[i] = dp[i - 1] + dp[i - 2];
3,dp[0] = 0,dp[1] = 1;
4,从前向后遍历;
5,可以打印数组debug;
class Solution {public int fib(int n) {int[] dp = new int[31];dp[0] = 0;dp[1] = 1;for(int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}题目链接:70. 爬楼梯
代码随想录
视频:带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目_哔哩哔哩_bilibili
看完代码随想录之后的想法:
我们要知道动态规划的五部曲;
1,确定dp数组的含义,下标的含义;
2,确定递推公式;
3,确定dp数组如何初始化;
4,确定遍历顺序;
5,打印dp数组(用来debug)
1,dp[i]表示到达第i个台阶有dp[i]个方法;
2,dp[i] = dp[i - 1] + dp[i - 2];到达第i个台阶需要的方法等于到达第i - 1 的方法数加上 到达第i - 2 的方法数
3,dp[0] 没有意义,dp[1] = 1, dp[2] = 2;
4,从前向后遍历;
5,可以打印dp数组用来debug;
class Solution {public int climbStairs(int n) {int[] dp = new int[46];dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];}
}题目链接:59.螺旋矩阵II
文章讲解:代码随想录
视频讲解:一入循环深似海 | LeetCode:59.螺旋矩阵II
看完代码随想录之后的想法:
我们要知道动态规划的五部曲;
1,确定dp数组的含义,下标的含义;
2,确定递推公式;
3,确定dp数组如何初始化;
4,确定遍历顺序;
5,打印dp数组(用来debug);
1,dp[i] 的含义到达下标i的位置所需要的的di[i](最小花费);
2,递推公式dp[i] = Math.min((dp[i - 1] + cost[i - 1]), dp[i - 2] + cost[i - 2]);
dp[i] 的含义到达下标i的位置所需要的的最小花费;
dp[i - 1] 的含义到达下标i - 1的位置所需要的的最小花费 加上第i-1向上的花费
dp[i - 2] 的含义到达下标i - 2的位置所需要的的最小花费 加上第i-2向上的花费;
然后取最小值;
class Solution {public int minCostClimbingStairs(int[] cost) {int n = cost.length;int[] dp = new int[1001];for(int i = 2; i <= n; i++)dp[i] = Math.min((dp[i - 1] + cost[i - 1]), dp[i - 2] + cost[i - 2]);return dp[n];}
}总结:
昨天下午学了一会计组,但是晚上没有学,想要淘一个二手自行车,今天开始动态规划的入门,背了一个小时的英语单词;
相关文章:

代码随想录算法训练营第三十八天 | ● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯
题目链接:509. 斐波那契数 代码随想录 视频:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili 看完代码随想录之后的想法: 我们要知道动态规划的五部曲; 1,确定dp数组的含义&#x…...
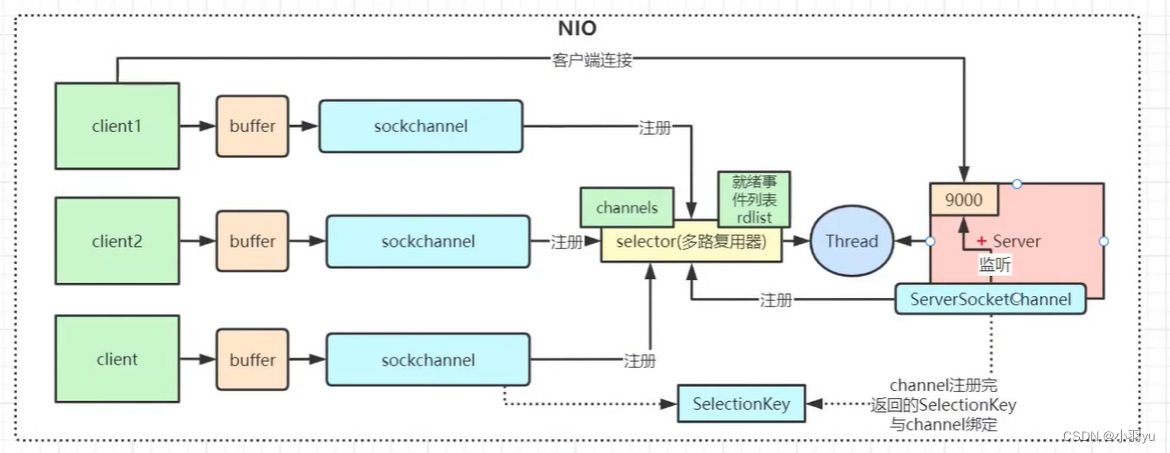
Java分别用BIO、NIO实现简单的客户端服务器通信
分别用BIO、NIO实现客户端服务器通信 BIONIONIO演示(无Selector)NIO演示(Selector) 前言: Java I/O模型发展以及Netty网络模型的设计思想 BIO Java BIO是Java平台上的BIO(Blocking I/O)模型&a…...

React Portals
什么是React Portals React Portals(React 门户)是 React 提供的一种机制,用于将组件渲染到 DOM 树中的不同位置,而不受组件层次结构的限制。它允许你将一个组件的渲染内容“传送”到 DOM 结构中的任何位置,通常用于处…...

Python基础之高级函数
异常捕获 Python中,使用trycatch两个关键字来实现对异常的处理。在我们平时的工作中,异常的出现是在所难免的,但是异常一旦出现,极有可能会直接导致程序崩溃,无法正常运行,所以异常一定要及时的做出对应的…...
CSS3常用的新功能总结
CSS3常用的新功能包括圆角、阴渐变、2D变换、3D旋转、动画、viewpor和媒体查询。 圆角、阴影 border-redius 对一个元素实现圆角效果,是通过border-redius完成的。属性为两种方式: 一个属性值,表示设置所有四个角的半径为相同值ÿ…...
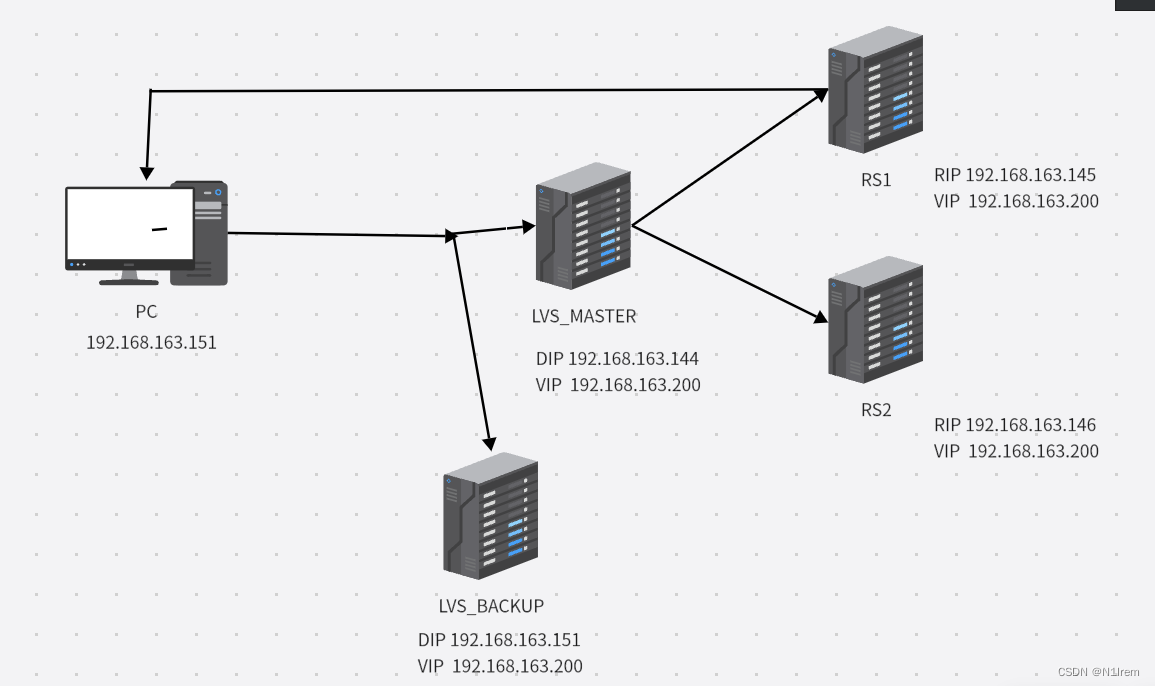
Lvs+KeepAlived高可用高性能负载均衡
目录 1.环境介绍 2.配置keepalived 3.测试 1.测试负载均衡 2.测试RS高可用 3.测试LVS高可用 3.1测试lvs主服务宕机 3.2.测试lvs主服务器恢复 4.我在实验中遇到的错误 1.环境介绍 环境:centos7 RS1---RIP1:192.168.163.145 VIP 192.168.163.200 RS2---RIP2…...

无涯教程-Android Online Test函数
Android在线测试模拟了真正的在线认证考试。您将看到基于 Android概念的多项选择题(MCQ),将为您提供四个options。您将为该问题选择最合适的答案,然后继续进行下一个问题,而不会浪费时间。完成完整的考试后,您将获得在线考试分数。 总问题数-20 最长时间-20分钟 Start Test …...

蓝桥杯打卡Day1
文章目录 全排列八皇后 一、全排列IO链接 本题思路:本题是一道经典的全排列问题,深度优先搜索即可解决。 #include <bits/stdc.h>constexpr int N10;std::string s; std::string ans; int n; bool st[N];void dfs(int u) {if(un){std::cout<<ans<…...

zipkin2.24.2源码install遇见的问题
1、idea导入项目后将Setting中的关于Maven和Java Compile相关的配置改为jdk11,同时Project Structure改为jdk11 2、将pom配置中的fork标签注释 标题未修改以上配置产生的问题 Compilation failure javac: Ч ı : --release : javac <options> <source files&g…...
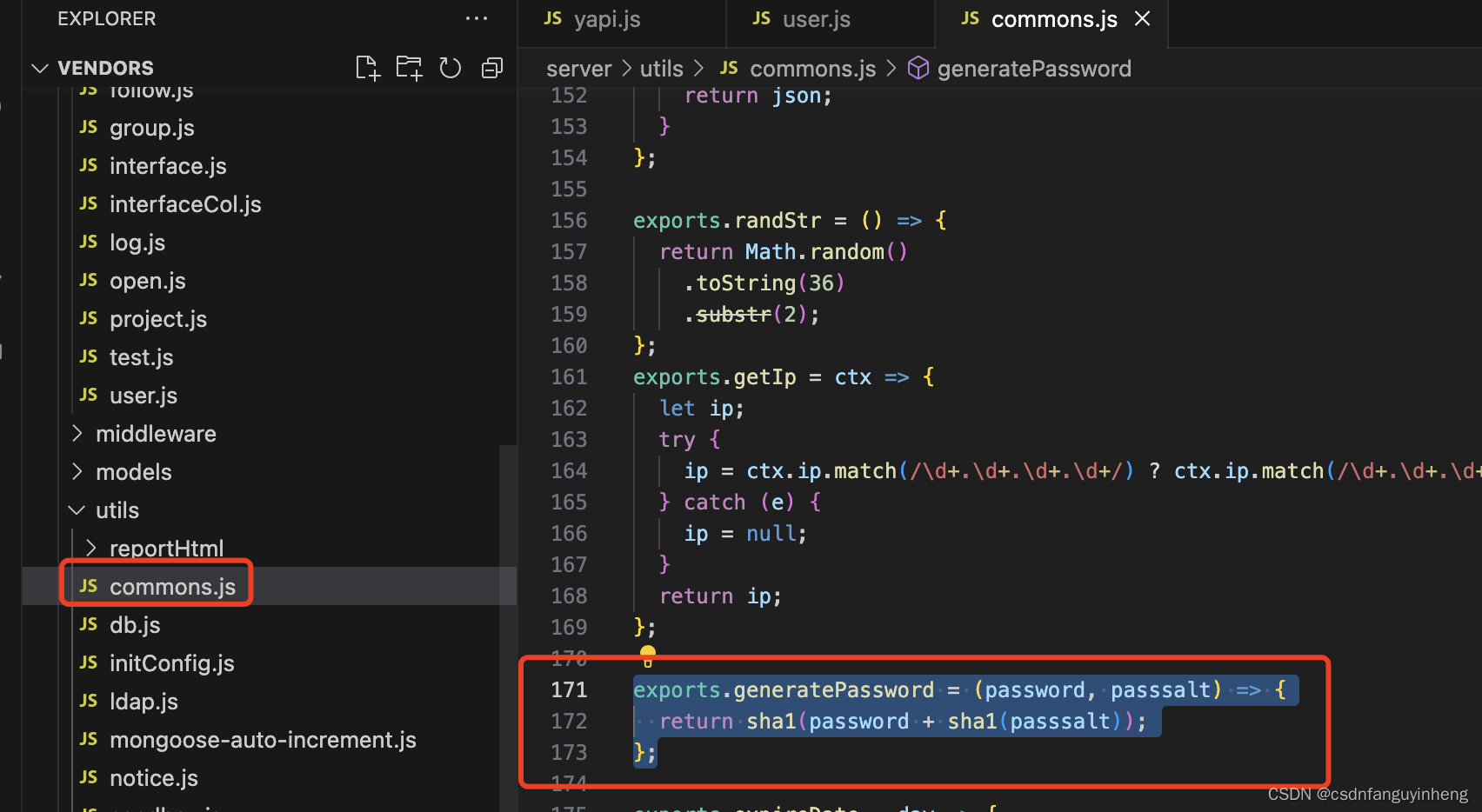
yapi密码是如何生成的
yapi密码是如何生成的 关闭yapi注册功能后,想要通过手动插入用户数据到db中,那么密码是如何生成的呢? exports.generatePassword (password, passsalt) > { return sha1(password sha1(passsalt)); }; 所以如果想要创建一个用户&#x…...

2023-09-02 LeetCode每日一题(最多可以摧毁的敌人城堡数目)
2023-09-02每日一题 一、题目编号 2511. 最多可以摧毁的敌人城堡数目二、题目链接 点击跳转到题目位置 三、题目描述 给你一个长度为 n ,下标从 0 开始的整数数组 forts ,表示一些城堡。forts[i] 可以是 -1 ,0 或者 1 ,其中&…...
k8s环境部署配置
目录 一.虚拟机准备 二.基础环境配置(各个节点都做) 1.IP和hosts解析 2.防火墙和selinux 3.安装基本软件 4.配置时间同步 5.禁用swap分区 6.修改内核参数并重载 7.配置ipvs 三.docker环境(各个节点都做) 1.配置软件源并…...
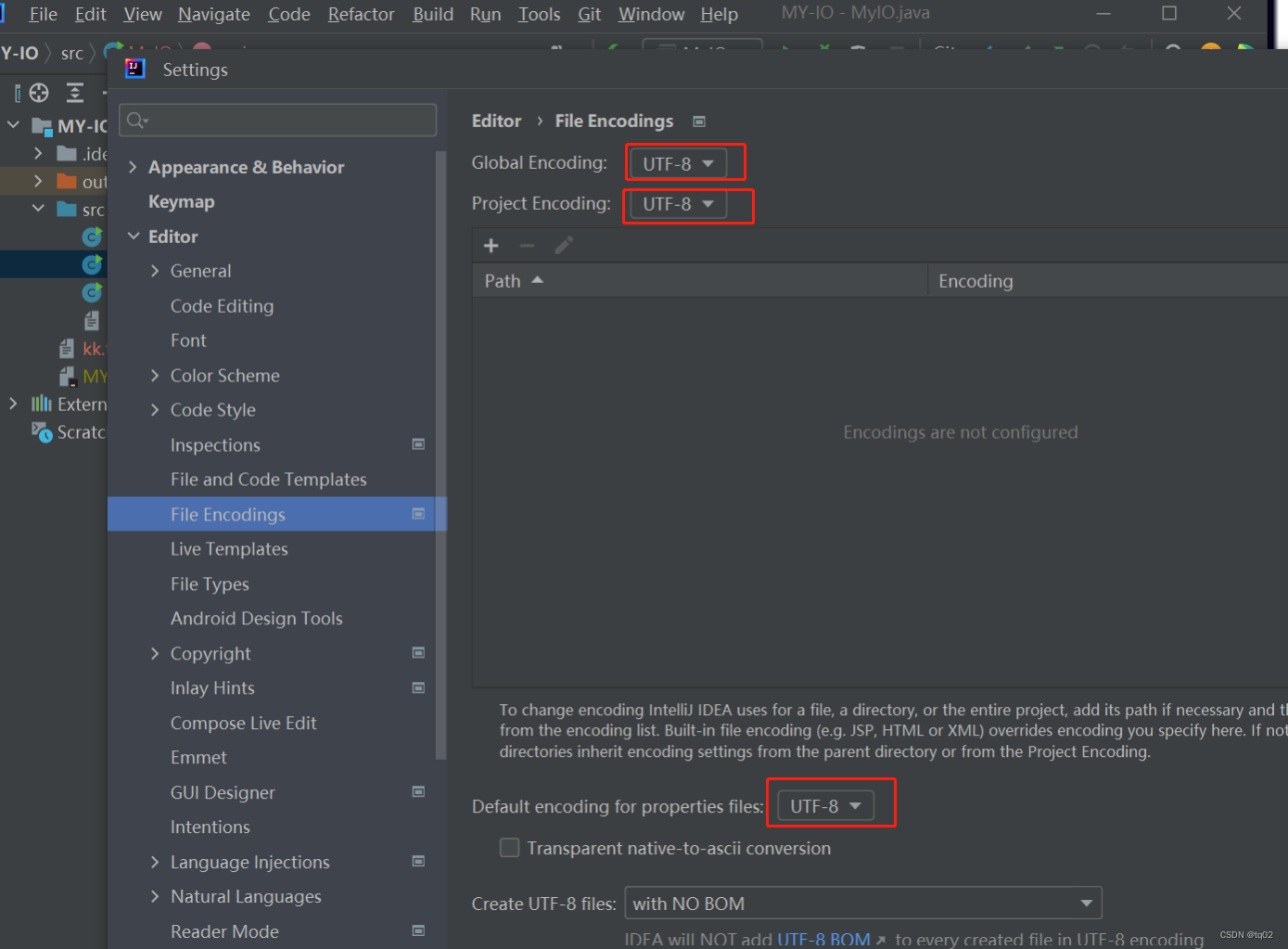
Java之文件操作与IO
目录 一.认识文件 1.1文件是什么? 1.2文件的组织 1.3文件路径 1.4文件的分类 二.文件操作 2.1File概述 三.文件内容操作--IO 3.1JavaIO的认识 3.2Reader和Writer ⭐Reader类 ⭐Writer类 3.2FileInputStream和FileOutputStream ⭐FileInputStream类 …...

指令系统(408)
一、拓展操作码指令格式 【2017 统考】某计算机按字节编址,指令字长固定且只有两种指令格式,其中三地址指令29条、二地址指令107条,每个地址字段6位,则指令字长至少应该是( A) A、24位 B、26位 …...
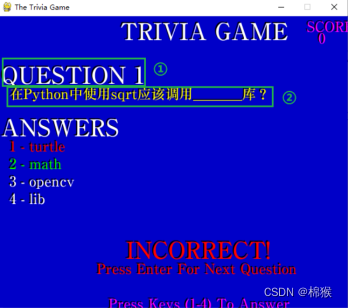
Pygame中Trivia游戏解析6-3
3.3 Trivia类的show_question()函数 Trivia类的show_question()函数的作用是显示题目。主要包括显示题目框架、显示题目内容和显示题目选项等三部分。 3.3.1 显示题目的框架 在show_question()函数中,通过以下代码显示题目的框架。 print_text(font1, 210, 5, &q…...
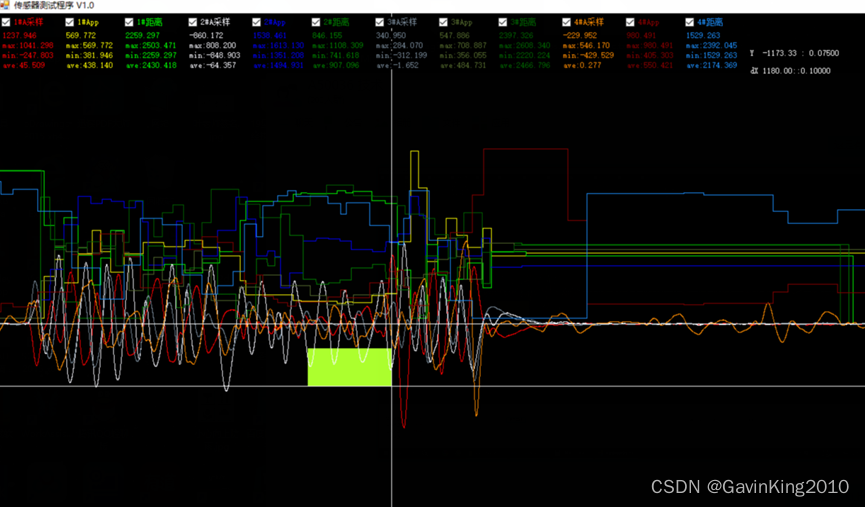
热释电矢量传感器设计
1 概述 使用4个热释电传感器组成一个2X2的矩阵。通过曲线的相位差、 峰峰值等特征量来计算相关信息。本文使用STM32单片机设计、制作了热释电传感器矩阵;使用C#.NET设计了上位机软件。为以上研究做了试验平台。 2 硬件电路设计 2.1 热释电传感器介绍 热释电红外…...

MySql学习笔记10——视图介绍
视图 概述 view view可以看作是一张“虚拟表”,(但是他也是会作为文件存在的) 当我们通过复杂的查询语句获取一张表的时候,可以将这张表作为一个视图,和创建一个新表不同,在视图上进行的DML操作会对数据…...

【探索Linux】—— 强大的命令行工具 P.7(进程 · 进程的概念)
阅读导航 前言一、冯诺依曼体系结构二、操作系统(OS)1. 概念 三、进程1. 进程的概念2. PCB(Process Control Block)3. 查看进程 四、fork函数1. 函数简介2. 调用方式3. 返回值4. 使用示例 五、进程的几种状态1. 状态简介2. 进程状…...
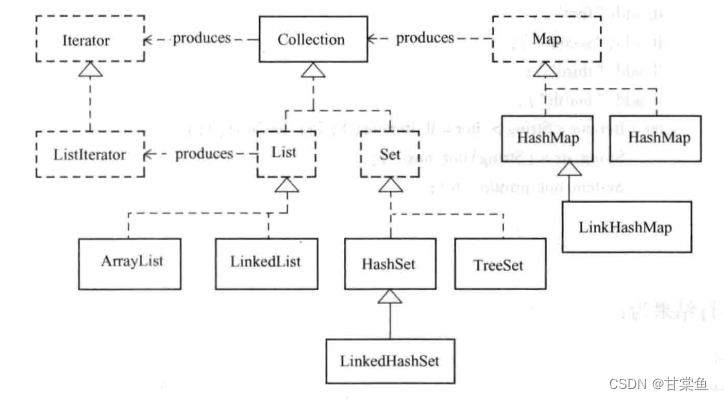
JAVA宝典----容器(理解记忆)
目录 一、Java Collections框架是什么? 二、什么是迭代器? 三、Iterator与ListIterator有什么区别? 四、ArrayList、Vector和LinkedList有什么区别? 五、HashMap、Hashtable、TreeMap和WeakHashMap有哪些区别? 六…...
)
JS中的扩展操作符...(点点点)
标题 前言概述拓展操作符(Spread Operator)赋值与扩展操作符的区别 剩余操作符(Rest Operator) 前言 大家应该都在代码中用过或者看到…方法,我每次用到这个方法的时候都会想到第一次见到这个方法一头雾水的样子&#…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
