普通平衡树 Splay
Splay 简介
Splay(伸展树),又叫做分裂树,是一种自调整形式的二叉查找树,满足二叉查找树的性质:一个节点左子树的所有节点的权值,均小于这个节点的权值。且其右子树所有节点的权值,均大于这个节点的权值。
因此Splay的中序遍历是一个递增序列。
Splay可以用来维护实链剖分(LCT)等,作为普通平衡树,它的优势在于不需要记录用于平衡树的冗余信息。
Splay维护一个有序集合,支持如下操作:
- 向集合中添加一个数
- 删除集合中的一个数
- 求出一个数的排名
- 根据排名求出这个数
- 查找一个数的前驱
- 查找一个数的后继
Splay原理以及实现
模板题
约定
为了代码简洁以及安全,我们用数组模拟Splay,并且做出规定如下性质:
- 安全性:不在Splay上的节点,以及被删除的节点,其所有信息应该被清空。
- 保证:我们保证函数不可能被非法调用,或者所有可能的非法调用是无害的,因此不需要在被调用的函数内部进行特判。
例如:我们保证get(u)中,u一定有父亲。
例如:push_up(0)是无害的。 - 代码重用:我们尽可能的保证代码重用
- 节点从
1开始编号,0号节点可能有多余的子孙/后代信息,但是其val,cnt,siz信息始终为0。
或许每一个约定都并不是完全必要的。
节点:node
Splay上的一个节点(node)维护这样几个信息:
fa:这个节点的父亲编号,fa=0表示没有父亲ch[0]:节点的左儿子编号,ch[0]的别名是l,若l=0表示没有左儿子ch[1]:节点的右儿子编号,ch[1]的别名是r,若r=0表示没有右儿子val:节点的权值cnt:节点权值在集合中出现的次数siz:以此节点为根的子树的大小- 成员函数
set(v,c,s):用来初始化节点信息,使得val=v,cnt=c,siz=s,并且让fa=l=r=0。其中c和s的默认值为1
const int N=2e6;
struct node {int fa,ch[2],val,cnt,siz;int&l=ch[0],&r=ch[1];void set(int v,int c=1,int s=1) {fa=l=r=0;val=v;cnt=c;siz=s;}
} t[N+5];
int tot,root;
左右儿子函数(get)
函数原型:
bool get(int);
函数get(u)返回编号为u的节点是其父亲的左儿子(返回0)或者右儿子(返回1),保证传入的参数u一定有父亲。
函数定义:
bool get(int u) {return t[t[u].fa].r==u;
}
上传(push_up)
函数原型:
void push_up(int);
函数push_up(u)将编号为u节点用自己的两个儿子的信息更新自己的siz信息。当有儿子编号为0时不影响,因为我们保证0号节点的siz信息为0。
函数定义:
void push_up(int u) {t[u].siz=t[t[u].l].siz+t[t[u].r].siz+t[u].cnt;
}
事实上push_up(0)也不影响0节点的siz,因为调用push_up(0)仅在pop函数中root=0时,但此时由于早已del了0节点的左右儿子,因此0节点必然没有左右儿子的信息。
加入节点(add)
函数原型:
void add(int,int,bool);
函数add(fa,son,k)将编号为son的节点加入Splay,并且它是父亲fa的k侧儿子。
函数定义:
void add(int fa,int son,bool k) {t[t[son].fa=fa].ch[k]=son;
}
删除节点(del)
函数原型:
void del(int);
函数del(u)将编号为u的节点从Splay中删除,这需要操作它的父亲和左右儿子,并且将它的三个权值(val,cnt,siz)清空。
函数定义:
void del(int u) {t[t[u].l].fa=t[t[u].r].fa=t[t[u].fa].ch[get(u)]=0;t[u].set(0,0,0);
}
旋转(rotate)
Splay的单次操作复杂度并不是严格 O ( log n ) O(\log n) O(logn)的,但是Splay依靠其伸展操作(splay)使得总复杂度为均摊 O ( n log n ) O(n\log n) O(nlogn)(而不是期望 O ( n log n ) O(n\log n) O(nlogn))的。
在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
函数原型
void rotate(int);
当树是完全二叉树时,单次查询复杂度为 O ( log n ) O(\log n) O(logn)
当树是一条链时,单次查询复杂度为 O ( n ) O(n) O(n)
rotate通过改变树的形态,达到使得Splay的均摊复杂度为 O ( log n ) O(\log n) O(logn)的目的。
函数rotate(u)将编号为u的节点旋转一次。
旋转原理
首先我们需要记录一个变量k:
k=get(u)
这表明了编号为u的节点是其父亲的哪侧儿子,k=0表示左儿子,k=1表示右儿子。
旋转过程需要保存几个节点编号:
u:当前节点fa:当且节点的父亲son:节点t[u]的异侧儿子,即son=t[u].ch[k^1]。例如:如果t[u]是t[fa]的左儿子,那么t[son]就是t[u]的右儿子。ffa:当前节点的父亲的父亲。
画出一个图来示意一下:
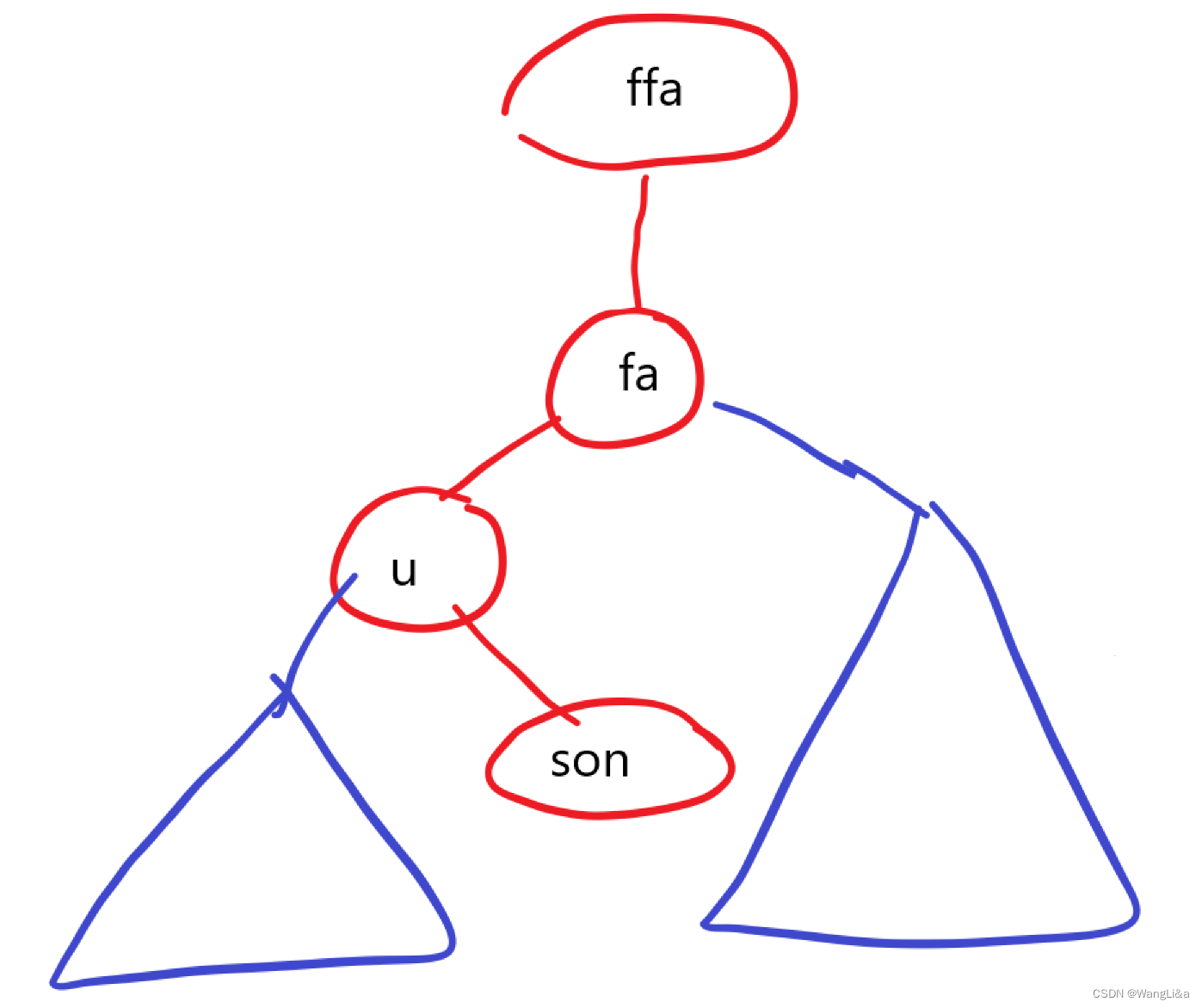
在这里,t[fa]是t[ffa]的哪侧儿子无关紧要。
接下来我们修改树的形态,完成三步操作:
- 用
u顶替掉原来fa的位置: 把u设置为ffa的儿子,fa是哪侧儿子,u就是哪侧儿子。 - 用
fa顶替掉原来son的位置:fa变成u的k^1儿子 - 把
son设为fa的同侧儿子,替代u:son变成fa的k儿子
还是看代码比较好懂:
int k=get(u),son=t[u].ch[k^1],fa=t[u].fa,ffa=t[fa].fa;
add(ffa,u,get(fa));
add(u,fa,k^1);
add(fa,son,k);
画个图:
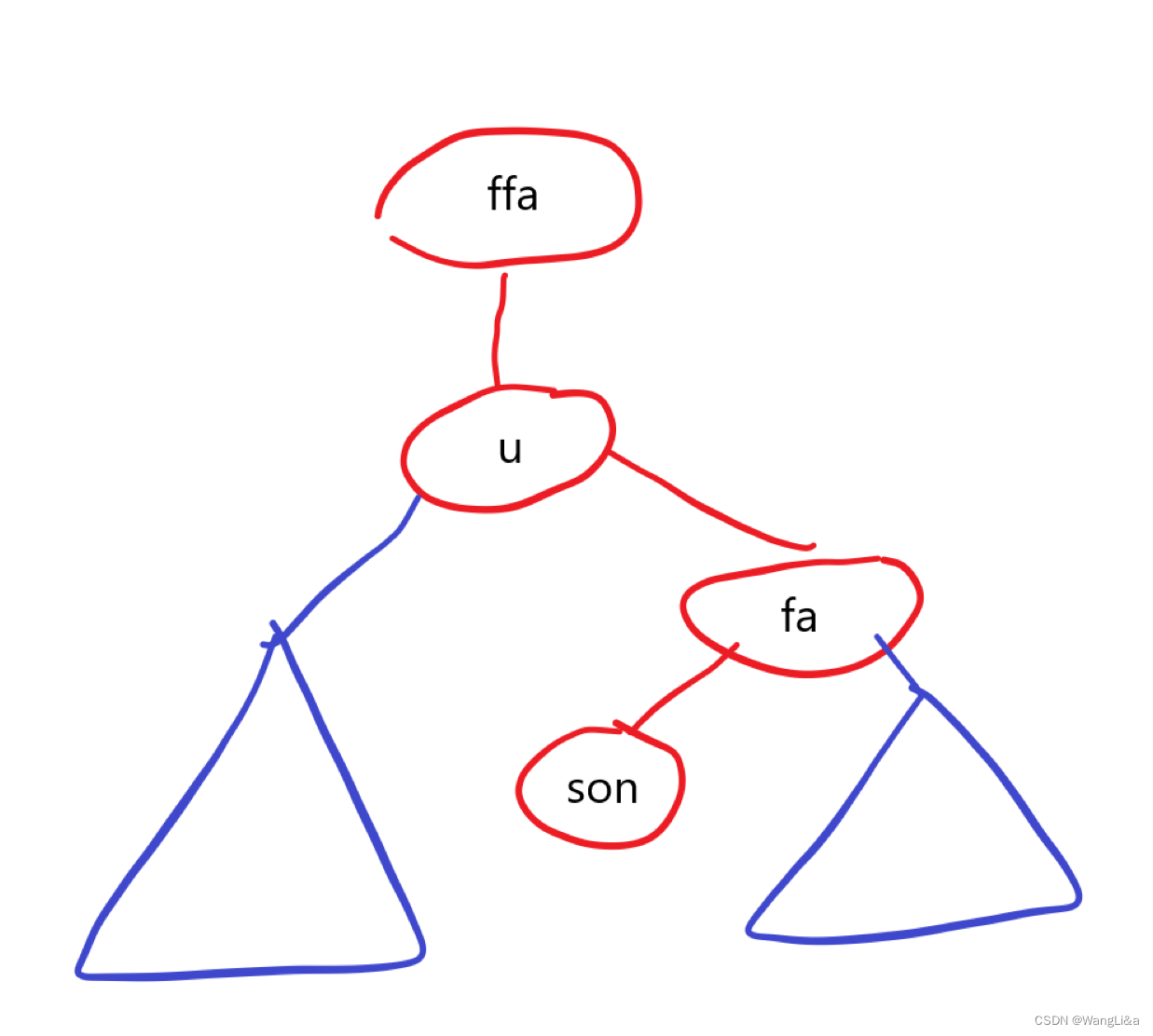
直接背下来写得比较快。
旋转实现
完整代码是这样的:
void rotate(int u) {int k=get(u),son=t[u].ch[k^1],fa=t[u].fa,ffa=t[fa].fa;add(ffa,u,get(fa));add(u,fa,k^1);add(fa,son,k);push_up(fa);push_up(u);
}
注意最后要更新节点信息。先push_up父亲,再push_up自身,因为此时,原来的父亲是自身的儿子。
保证编号为u的节点存在父亲。
(事实上,可能会有son=0或ffa=0,使得编号为0的节点可能携带有额外的祖先/后代信息,但是这不影响。)
其实我们还可以选择把子孙转成指定祖先的儿子处就停止,这里不多说了。
伸展(splay)
函数原型:
int splay(int);
伸展操作是执行若干次旋转操作,把编号为u的节点旋转到根,并返回u的编号。
执行的方法是这样的:
记录当且节点的编号u,更新它目前的父亲编号fa=t[u].fa,注意u的父亲是不断变化的,因此要更新:
- 如果
u没有父亲,说明u是根节点:停止 - 如果
fa不存在父亲,说明u再旋转一次就会旋转到根:rotete(u) get(fa)==get(u),说明u和fa是同侧儿子,先旋转fa,再旋转u:rotate(fa),rotate(u)get(fa)!=get(u),说明u和fa是异侧儿子,旋转两次u:rotate(u),rotate(u)
写成代码是这样的:
int splay(int u) {for(int fa; (fa=t[u].fa); rotate(u))if(t[fa].fa)rotate(get(u)==get(fa)?fa:u);return root=u;
}
注意最后把根节点编号设为u。
伸展主要有三个作用:
- 可以保证时间复杂度
rotate内有push_up函数,如果修改了u的信息,伸展一下可以更新到根节点的链上信息- 把
u旋转到根便于下一步操作
加入值(push)
函数原型:
int push(int);
函数push(val)将val在集合中出现的次数增加1,并返回val所在的节点编号,如果val在集合中原来并不存在,就创建一个新节点。
函数分为三种情况讨论:
- Splay为空:直接新建一个节点,然后把根设为这个节点。
- Splay中以前存在
val这个值:找到存储这个值的节点,先把它旋转到根,然后把它的cnt增加1,再push_up以更新信息。
(因为此时这个节点已经是根了,对它调用splay不会rotate,因此必须手动psuh_up。
即使我们先前不把这个节点旋转到根,但是这个节点可能原本就是根,还是需要更新一下siz信息) - Splay中不存在
val这个值:找到一个合适的叶子节点,然后对val新建一个节点,并且把新节点的父亲设为这个叶子节点。把这个节点旋转到根。
为了保证时间复杂度,同时为了更新链上记录的siz信息,最后都要把val所在的节点旋转到根。
函数定义:
int push(int val) {if(!root) {t[++tot].set(val);return root=tot;}int x=val_find(val);这里的val_find函数很特殊,如果找到val,会返回这个节点作为根节点,否则会返回一个可以作为新节点父亲的叶子节点if(t[x].val==val) {t[x].cnt++;push_up(x);return x;}t[++tot].set(val);要先set再加边,否则set会将t[tot]上存储的祖先/子孙信息清除add(x,tot,t[x].val<val);return splay(tot);
}
删去值(pop)
函数原型:
void pop(int);
函数pop(val)将集合中val出现的次数减1,保证val之前至少出现过一次。
函数分几种情况讨论:
首先找到val所在的节点的编号,设为u,然后把这个节点旋转到根。
- 如果
t[u].cnt>1:直接让cnt-- - 如果
u至少没有一个儿子,那就把根设为它的另一个儿子,然后删除u。
(如果u没有任何一个儿子是不影响的。) - 否则,说明
u既有左儿子,又有右儿子,也就是说val既有前驱又有后继:
因此找到val的前驱,把前驱旋转到根,此时u一定是根的右儿子,而且由于根是前驱,所以u没有左儿子,因此直接把u的右儿子设为根的右儿子,然后删除u即可。
注意最后要push_up(root),因为第1,3种情况下需要更新根节点信息。
函数实现:
void pop(int val) {int u=val_find(val);if(t[u].cnt>1) t[u].cnt--;else if(!t[u].l||!t[u].r) root=t[u].l|t[u].r,del(u);else {pre(val);int r=t[u].r;del(u);这里要先清除u,再连边。否则清除u时会顺便擦除根节点和r节点的祖先关系信息add(root,r,1);此时前驱是根节点,把u的右儿子设为其前驱的右儿子}push_up(root);
}
用值查找(val_find)
函数原型:
int val_find(int);
函数val_find(val)在集合中查找值val,如果它出现过,那就把val所在的节点旋转到根,并且返回它的编号,如果它没有出现过,那就返回一个可以作为val父亲的叶子节点编号。
(如果此时树为空,函数会返回0,尽管不会出现这样的调用)
主要做法就是从根节点开始找,如果找到了就返回,没找到就按照大小关系继续往下走。
如果找到叶子节点还没找到val就返回它的父亲。
函数定义:
int val_find(int val) {int u=root,fa=0;while(u)if(t[fa=u].val==val) return splay(u);else u=t[u].ch[t[u].val<val];return fa;
}
用排名查找(rank_find)
函数原型:
int rank_find(int,int);
函数rank_find(u,rank)查找u子树内排名为rank的节点,并返回节点编号。注意这里是子树内排名,而不是全局排名。
我们通常调用时参数u=root,即查询全局排名。
把rank_find函数设计为两个参数,一方面是为了方便递归调用,另一方面,不为其提供一个参数的重载版本是为了防止将其与val_find函数与find_rank函数混淆。
rank_find(u,rank)函数这样设计:
分情况讨论:
- 如果
rank<=左子树大小,递归到左儿子:rank_find(t[u].l,rank) - 否则,如果
rank>左子树大小+自身节点的cnt,递归到右儿子:rank_find(t[u].r,rank-t[t[u].l].siz-t[u].cnt) - 否则:旋转并且返回自身节点编号
这种独特的递归顺序使得如果查询的rank大于子树之内的最大排名,会返回子树最大值的节点编号,避免了进一部的分情况讨论。
函数定义:
int rank_find(int u,int rank) {int l=t[t[u].l].siz;这样可以少打很多字if(rank<=l) return rank_find(t[u].l,rank);else if(rank>l+t[u].cnt) return rank_find(t[u].r,rank-l-t[u].cnt);return splay(u);
}
查询值的排名(find_rank)
函数原型:
int find_rank(int);
函数find_rank(val)查询值val的排名,不保证val出现过。
没有提供查询节点排名的函数是因为节点不存在排名,如果想要查询节点u对应的权值的排名,可以调用find_rank(t[u].val)。
查询val的排名,可以通过把val加入集合一次,然后把它对应的节点旋转到根。那么val的排名就是它对应节点的左子树的大小+1。
然后再把val在集合中删去一次。
函数定义:
int find_rank(int val) {int ans=t[t[push(val)].l].siz+1;pop(val);return ans;
}
查找前驱/后继(bound)
函数原型:
int bound(int,bool);
函数bound(val,k)用于查询前驱/后继,旋转节点到根,并返回对应的节点编号。
函数bound(val,0)用于查询值val的前驱。
函数bound(val,1)用于查询值val的后继。
bound原理
这里以查询前驱举例:
查询val前驱的方法就是,无论Splay中是否存在val,我们都先push(val),这样Splay内肯定存在val,且为Splay的根。
走到根的左儿子上,然后不断地走右儿子,直到走到叶子节点即为前驱,记录答案后pop(val)。
查询后继的方法是类似的:先push(val),走到根的右儿子上,然后不断地走左儿子,叶子节点即为前驱,记录答案后pop(val)。
注意到可以把这两种情况合并起来:设k=0表示查询前驱,k=1表示查询后继,则函数定义如下:
int bound(int val,bool k) {int u=t[push(val)].ch[k];while(t[u].ch[k^1]) u=t[u].ch[k^1];pop(val);return splay(u);
}
前驱(pre)
函数原型:
int pre(int);
pre为查询前驱提供了专门的接口。
函数pre(val)表示查询val的前驱,把前驱旋转到根,并且返回前驱编号。
val可以比集合中的任何数都要大,但是不能没有前驱,否则运行可能出现问题,我们没有保证splay(0)不会出错,因为我们没有保证t[0]不携带非零的祖先后代信息。
如果非要这样查询可能没有前驱/后继的数的话可以设置哨兵:push(-INF),push(INF)
函数定义:
int pre(int val) {return bound(val,0);
}
后继(nxt)
函数原型:
int nxt(int);
函数nxt(val)表示查询val的后继,把后继旋转到根,并返回后继编号。
必须要保证val有后继。
函数定义:
int nxt(int val) {return bound(val,1);
}
完整代码
空间复杂度
注意到Splay的任意一种操作至多创建一个节点,因此空间复杂度为一倍操作次数。(本题要算上一开始的 1 0 5 10^5 105次操作)
代码
#include<iostream>
using namespace std;
const int N=2e6;
struct node {int fa,ch[2];int val,cnt,siz;int &l=ch[0],&r=ch[1];void set(int v,int c=1,int s=1) {l=r=fa;val=v;cnt=c;siz=s;}
}t[1100005];
int tot,root;
bool get(int);
void push_up(int);
void add(int,int,bool);
void del(int);
void rotate(int);
int splay(int);
int push(int);
void pop(int);
int val_find(int);
int rank_find(int,int);
int find_rank(int);
int bound(int,bool);
int pre(int);
int nxt(int);
int a[N+5];
int main() {int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) push(a[i]);int ans=0,last=0;while(m--) {int op,x;cin>>op>>x;
// if(op==1) push(x);
// if(op==2) pop(x);
// if(op==3) cout<<find_rank(x)<<endl;
// if(op==4) cout<<t[rank_find(root,x)].val<<endl;
// if(op==5) cout<<t[pre(x)].val<<endl;
// if(op==6) cout<<t[nxt(x)].val<<endl;x^=last;if(op==1) push(x);if(op==2) pop(x);if(op==3) ans^=(last=find_rank(x));if(op==4) ans^=(last=t[rank_find(root,x)].val);if(op==5) ans^=(last=t[pre(x)].val);if(op==6) ans^=(last=t[nxt(x)].val);}cout<<ans;
}
bool get(int u) {return t[t[u].fa].r==u;
}
void push_up(int u) {t[u].siz=t[t[u].l].siz+t[t[u].r].siz+t[u].cnt;
}
void add(int fa,int son,bool k) {t[t[son].fa=fa].ch[k]=son;
}
void del(int u) {t[t[u].l].fa=t[t[u].r].fa=t[t[u].fa].ch[get(u)]=0;t[u].set(0,0,0);
}
void rotate(int u) {int k=get(u),son=t[u].ch[k^1],fa=t[u].fa,ffa=t[fa].fa;add(ffa,u,get(fa));add(u,fa,k^1);add(fa,son,k);push_up(fa);push_up(u);
}
int splay(int u) {for(int fa;(fa=t[u].fa);rotate(u)) if(t[fa].fa)rotate(get(fa)==get(u)?fa:u);return root=u;
}
int push(int val) {if(!root) {t[++tot].set(val);return root=tot;}int x=val_find(val) ;if(t[x].val==val) {t[x].cnt++;push_up(x);return x;}t[++tot].set(val);add(x,tot,t[x].val<val);return splay(tot);
}
void pop(int val) {int u=val_find(val);if(t[u].cnt>1) t[u].cnt--;else if(!t[u].l||!t[u].r) root=t[u].l|t[u].r,del(u);else {pre(val);int r=t[u].r;del(u);add(root,r,1);}push_up(root);
}
int val_find(int val) {int u=root,fa=0;while(u) if(t[fa=u].val==val) return splay(u);else u=t[u].ch[t[u].val<val];return fa;
}
int rank_find(int u,int rank) {int l=t[t[u].l].siz;if(rank<=l) return rank_find(t[u].l,rank);else if(rank>t[u].cnt+l) return rank_find(t[u].r,rank-t[u].cnt-l);return splay(u);
}
int find_rank(int val) {int ans=t[t[push(val)].l].siz+1;pop(val);return ans;
}
int bound(int val,bool k) {int u=t[push(val)].ch[k];while(t[u].ch[k^1]) u=t[u].ch[k^1];pop(val);return splay(u);
}
int pre(int val) {return bound(val,0);
}
int nxt(int val) {return bound(val,1);
}
后话
关于pop和pre
有一种观点认为,对pre函数查询不在集合里面的val会导致创建新节点,而删除val时又有可能导致查询val的前驱,这可能会导致循环调用。
但是这种说法是错误的,因为事实上,如果在pop(val)时调用pre(val),进而导致了一次push(val)后再pop(val),此时val对应节点的cnt至少为2了,所以在本层pop(val)不会调用pre(val),而是会将cnt--。
后记
于是皆大欢喜。
相关文章:

普通平衡树 Splay
Splay 简介 Splay(伸展树),又叫做分裂树,是一种自调整形式的二叉查找树,满足二叉查找树的性质:一个节点左子树的所有节点的权值,均小于这个节点的权值。且其右子树所有节点的权值,均…...

复旦-华盛顿EMBA:走近亿咖通科技,探寻汽车智能化的科创“密码”
6月20日,应复旦大学-华盛顿大学EMBA项目18班校友周靖的邀请,项目校友参访了科创企业ECARX亿咖通科技。作为该公司资深副总裁、中国首席财务官,周靖带领大家通过产品演示、实车驾驶和交流对话探寻汽车智能化的科创“密码”,近距离感…...

学习心得07:C#
之前也没有看过C#的书,C#的程序倒是搞了一些。好在项目不大,我又会套路。 C#很象是JAVA。好像就是JAVA出来之后,微软抄的。好东西就要学习,这不丢脸。 我倒是想,有没有办法把JAVA和C#进行映射,然后直接编译…...

importlib的使用、9个视图子类、视图集、drf之路由、drf之请求响应回顾、GenericViewSet相关流程图
一 drf之请求响应回顾 # 1 drf请求-请求对象:data,query_params,其他跟之前一样,FILES-默认:支持三种编码-局部配置:视图类中-from rest_framework.parsers import JSONParser, FormParser, MultiPartPars…...

国际站阿里云服务器远程桌面密码错误怎么办?苹果手机如何远程登录?
阿里云服务器是云计算领域的一种重要服务,它可以帮助用户在云端部署和管理自己的应用程序和网站。但是,有时候用户可能会遇到远程桌面密码错误的问题,导致无法登录到服务器。本文将介绍一些解决办法,以及如何使用苹果手机远程登录…...
CRMEB多端多语言系统文件上传0Day代审历程
Git仓库: https://github.com/crmeb/CRMEB简介: 两天攻防中,某政局子公司官网后台采用的CRMEB开源商城CMS,挺奇葩,别问怎么总让我碰到这种东西,我也不知道,主打的就是一个魔幻、抽象。最后通过…...
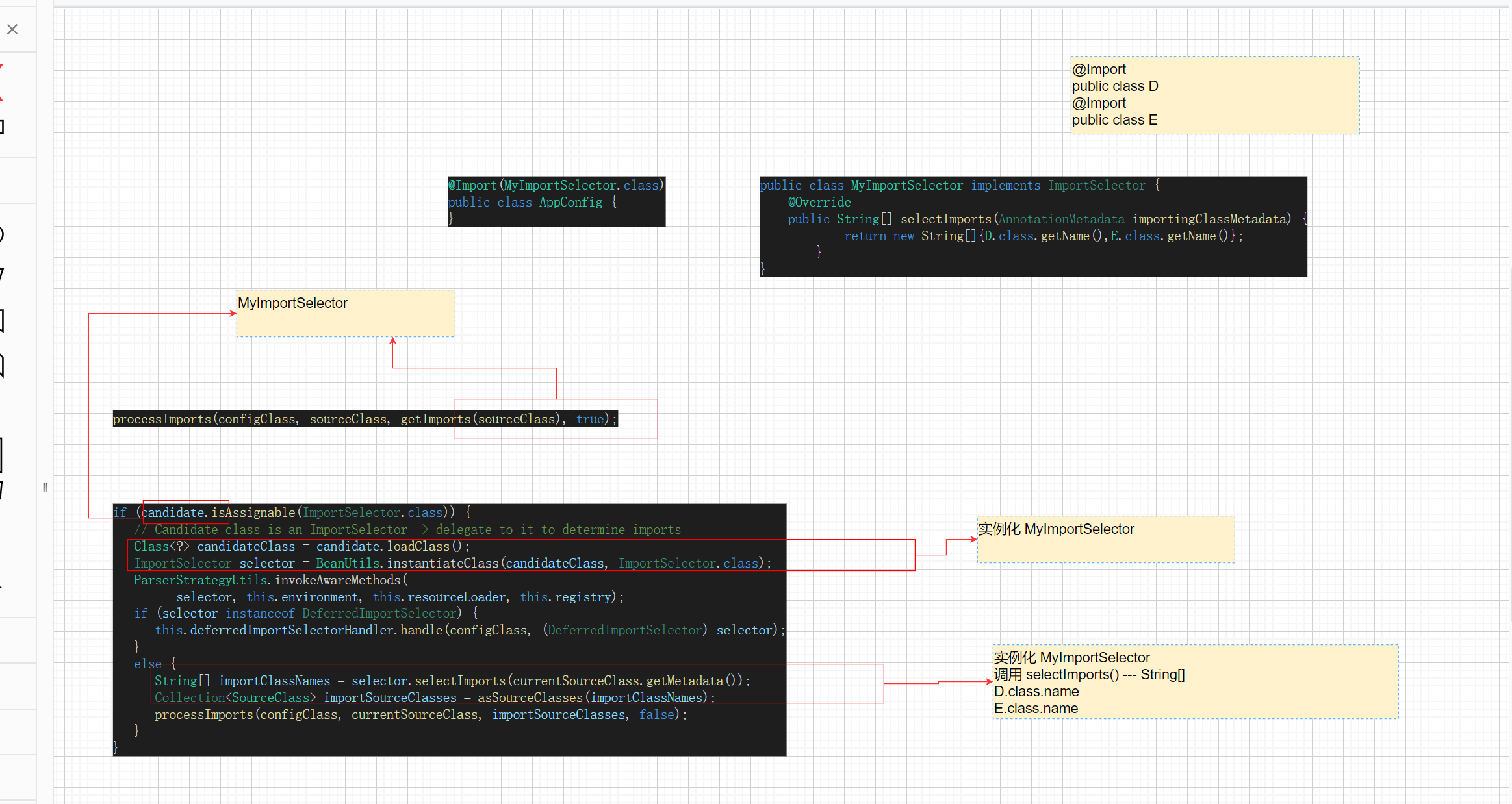
孙哥Spring源码第18集
第18集 refresh()-invokeBeanFactoryPostProcessor-二-ConfigurationClassPostProcessor的处理逻辑 【视频来源于:B站up主孙帅suns Spring源码视频】【微信号:suns45】 1、为什么PropertySource先处理? 因为Conponent A在处理的过程中 要把…...

【STM32】文件系统FATFS与Flash的初步使用
文件系统简介 简介可以不看,直接看移植步骤 文件系统是介于应用层和底层间的模糊层。底层提供API,比如说使用SDIO或者SPI等读写一个字节。文件系统把这些API组合包装起来,并且提供一些列函数,我们可以使用这些函数进行更进一步的…...
Android Glide in RecyclerView,only load visible item when page return,Kotlin
Android Glide in RecyclerView,only load visible item when page return,Kotlin base on this article: Android Glide preload RecyclerView切入后台不可见再切换可见只加载当前视野可见区域item图片,Kotlin_zhangphil的博客…...

【SCI征稿】3个月左右录用!计算机信息技术等领域均可,如机器学习、遥感技术、人工智能、物联网、人工神经网络、数据挖掘、图像处理
计算机技术类SCIE&EI 【期刊简介】IF:1.0-2.0,JCR4区,中科院4区 【检索情况】SCIE&EI 双检,正刊 【参考周期】期刊部系统内提交,录用周期3个月左右,走完期刊部流程上线 【征稿领域】计算机信息…...

Golang 中的 crypto/ecdh 包详解
什么是 ECDH 算法? ECDH(Elliptic Curve Diffie-Hellman)算法是一种基于椭圆曲线的密钥交换协议,用于安全地协商共享密钥(Secret Key),步骤如下: 1. 选择椭圆曲线:ECDH…...

系统学习live555
文章目录 系统学习live555系统学习LIVE555的步骤:1.了解基本概念:2.**查看官方文档:**3.**下载和编译库:**4.**阅读示例代码:**5.**了解库结构:**6.**创建简单项目:**7.**阅读更多文档ÿ…...
Linux下的系统编程——进程的执行与回收(八)
前言: 前面我们对进程已经有了一个初步的了解与认识,现在让我们学习一下进程中一些函数的具体使用,比如exec可以执行一些指定的程序,wait / waitpid可以回收子进程,什么是孤儿进程,什么是僵尸进程…...

第十九章 ObjectScript - 执行例程
文章目录 第十九章 ObjectScript - 执行例程执行例程New 命令 第十九章 ObjectScript - 执行例程 执行例程 执行例程时,使用DO命令,如下所示: do ^routinename要执行一个过程、函数或子程序(不访问其返回值),可以使用以下命令: do label^ro…...

Podman安装与使用
1.Podman简介 Podman是一个无守护进程的容器引擎,用于在Linux系统上开发、管理和运行OCI容器。 Podman的主要功能包括: 创建和管理容器:Podman可以创建、启动、停止和删除容器,以及管理容器的生命周期。容器镜像管理࿱…...

C++ 嵌套循环
一个循环内可以嵌套另一个循环。C 允许至少 256 个嵌套层次。 语法 C 中 嵌套 for 循环 语句的语法: for ( init; condition; increment ) {for ( init; condition; increment ){statement(s);}statement(s); // 可以放置更多的语句 }C 中 嵌套 while 循环 语句的…...

锁( ReentrantLock,Synchronized)
1.lock和synchronized 语法层面 synchronized 是关键字,源码在 jvm 中,用 c 语言实现; Lock 是接口,源码由 jdk 提供,用 java 语言实现; 使用 synchronized 时,退出同步代码块锁会自动释放&…...
)
主频计算-架构真题(二十三)
某文件系统采用多级索引结构,若磁块大小为4K字节,每个块号需占4个字节,那么采用二级索引结构时的文件最大长度可占用()个物理块。 1、1024 2、1024*1024 3、2048*2048 4、4096*4096 答案:B 解析&…...
docker安装redis实操记录
1.Docker拉取镜像 docker pull redis2.Docker挂载配置文件 创建挂载文件夹 mkdir -p /home/redis/data下载默认配置文件 redis.conf 3.启动redis 容器 docker run --restartalways --log-opt max-size100m --log-opt max-file2 -p 6379:6379 --name redis -v /home/redi…...

MobaXterm 突破14个session限制
通常情况下:随着工作时间的增长,我们会保存许许多多的linux到本地的mobastream,然后当超过14个,就会被被限制,这个会让人很头疼。 1. 安装python,配置好环境变量 测试安装成功: 2. 基于项目进行…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
