【算法系列篇】分治-归并

文章目录
- 前言
- 什么是归并算法
- 1. 排序数组
- 1.1 题目要求
- 1.2 做题思路
- 1.3 Java代码实现
- 2. 数组中逆序对
- 2.1 题目要求
- 2.2 做题思路
- 2.3 Java代码实现
- 3. 计算右侧小于当前元素的个数
- 3.1 题目要求
- 3.2 做题思路
- 3.3 Java代码实现
- 4. 翻转对
- 4.1 题目要求
- 4.2 做题思路
- 4.3 Java代码实现
- 总结
前言
上一篇算法文章,我们介绍了分治-快排的算法,今天我将为大家分享关于分治的另外一种算法——归并。
什么是归并算法
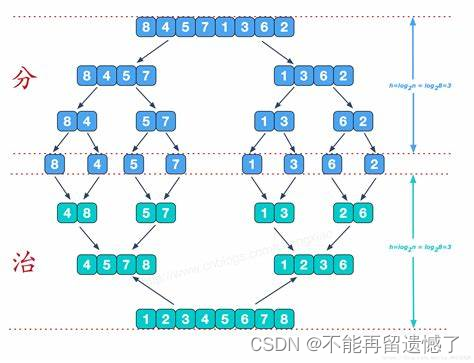
归并算法是一种常用的排序算法,它采用分治策略将待排序的数组分解为更小的子数组,然后逐步合并这些子数组以获得最终的有序数组。归并排序的主要思想是将两个有序的子数组合并成一个有序的数组。
归并算法通常包含以下步骤:
-
分解(Divide):将待排序的数组递归地分解为规模更小的子数组,直到每个子数组只有一个元素或为空。
-
解决(Conquer):通过递归地排序子数组,将其转化为有序的子数组。这通常是通过继续将子数组进一步分解并排序的方式实现的。
-
合并(Merge):将两个有序的子数组合并成一个有序的数组。该步骤的实现方式是比较两个子数组的元素,并按照顺序合并到一个新的数组中,直到所有元素都被合并。
归并排序的时间复杂度是O(nlogn),其中n是待排序数组的长度。它的主要优点包括:
-
稳定性:归并排序是一种稳定的排序算法,即相等元素的相对顺序不会被改变。
-
适用性:归并排序适用于各种数据结构,尤其在外部排序中,它对于大规模数据的排序效果明显。
然而,归并排序也存在一些缺点:
-
额外空间消耗:归并排序需要额外的空间来存储临时的子数组和合并结果,这可能对内存消耗造成一定影响。
-
递归调用:归并排序的实现通常使用递归调用,对于大规模数据的排序可能导致递归深度增加,从而增加了额外的函数调用开销。
总结而言,归并排序是一种高效、稳定的排序算法,通过分治策略将待排序的数组分解为更小的子数组,然后逐步合并这些子数组以获得最终的有序数组。尽管归并排序需要额外的空间和函数调用开销,但它在实践中被广泛使用,特别适用于对大规模数据进行排序。
1. 排序数组
https://leetcode.cn/problems/sort-an-array/
1.1 题目要求
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
- 1 <= nums.length <= 5 * 104
- -5 * 104 <= nums[i] <= 5 * 104
class Solution {public int[] sortArray(int[] nums) {}
}
1.2 做题思路
不知道大家是否做过将两个有序数组合并为一个有序数组,我们的归并算法就是通过将两个数组合并为一个有序数组来实现的。而归并的思想就是就一整个数组从中间将数组分为两个数组,然后再继续将这两个数组分别从中间分开,直到将这两部分的数组分为只有一个元素的两部分数组,然后将这两个数组通过合并两个数组的操作来进行合并,合并完成之后的数组就成为了一个有序的数组,然后继续将这两个有序的数组通过合并数组的操作继续进行合并,直到将这些数组合并为一个最大的数组。
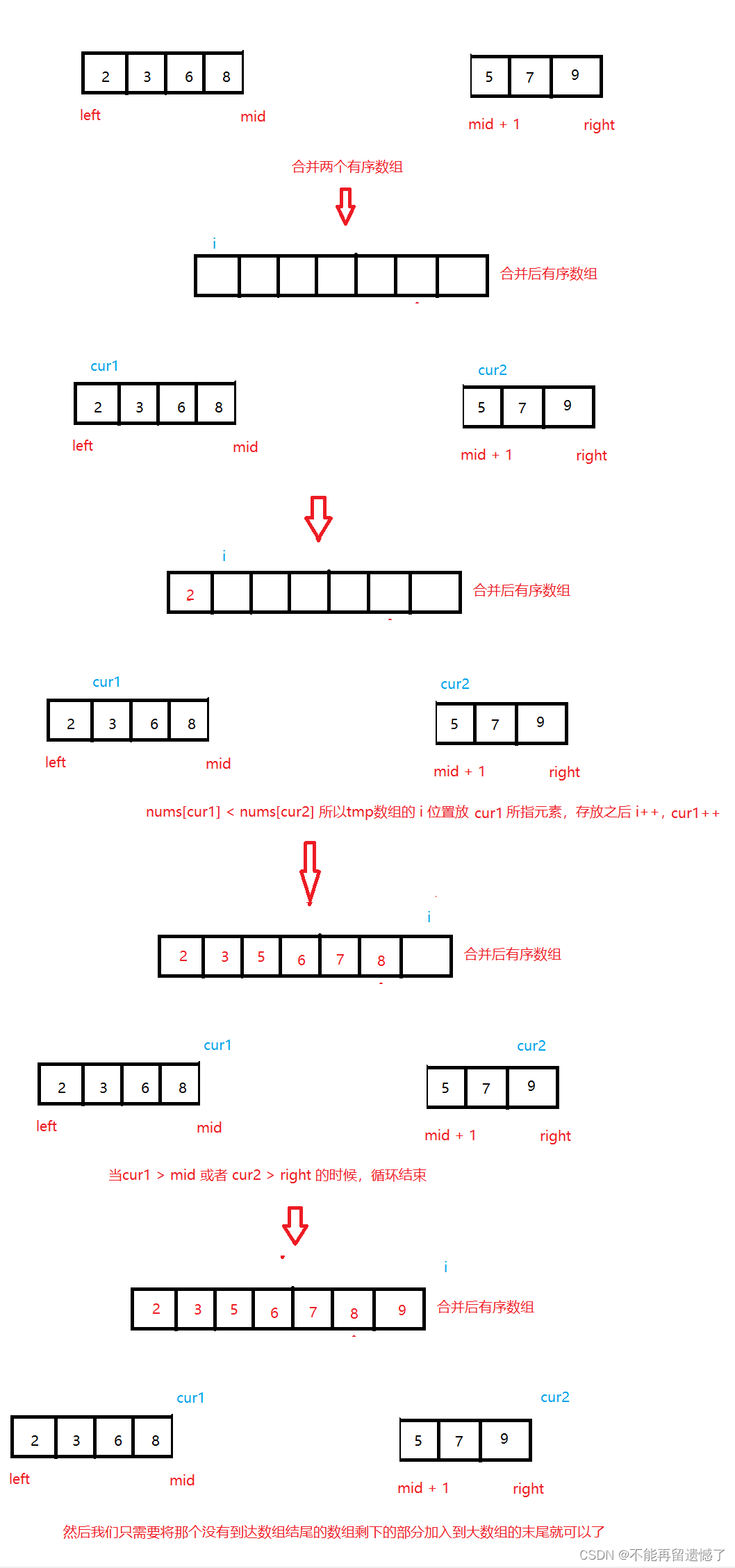
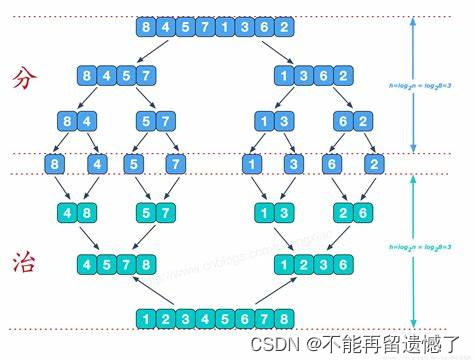
1.3 Java代码实现
class Solution {//因为每一次递归都需要创建临时的数组来存储两个数组排序之后的结果,//每次都向申请内存,速度会很慢//所以我们直接申请一个跟nums同样大小的数组int[] tmp;public int[] sortArray(int[] nums) {int n = nums.length;tmp = new int[n];mergeSort(nums,0,n -1);return nums;}private void mergeSort(int[] nums, int left, int right) {//当数组中只有一个元素或者区间不成立的时候,结束递归if(left >= right) return;int mid = left + (right - left) / 2;//先排序mid左右两边的数组,最后在将左右两边的有序数组进行合并mergeSort(nums,left,mid);mergeSort(nums,mid + 1,right);int cur1 = left,cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right) {tmp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];}//处理没到达数组结尾的数组while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];//将临时排序之后数组的结果更新到我们原本的数组中for(int j = left; j <= right; j++) nums[j] = tmp[j - left];}
}
2. 数组中逆序对
https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/
2.1 题目要求
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
限制:
- 0 <= 数组长度 <= 50000
class Solution {public int reversePairs(int[] nums) {}
}
2.2 做题思路
我们先来看看如何使用暴力解法来解决这个问题:用两层循环来遍历数组,i 从 0 开始,j 则从 i 的下一个位置开始,看 j 所指向的位置是否小于 i 所指的位置,如果是则逆序对总数加一。这样虽然简单,但是时间复杂度达到了 O(N^2),是跑不过去的,那么我们就需要对暴力解法进行优化,问题就在于我们该如何优化呢?
这样想,如果我们将数组分为两个部分,先计算左边部分的数组中的所有逆序对,然后计算右边部分数组中的所有逆序对,最后在左边数组一次选择一个数字,看右边数组中是否元素能与左边数组中的那个元素构成逆序对,这样的思路其实跟暴力解法是相同的,时间复杂度都是 O(N^2),那么当我们分别在左边数组中和右边数组中找到了符合的逆序对的话,我们是否可以将这两部分数组进行排序呢?当进行了排序之后,再分别在左边数组中依次拿元素与右边数组中的元素进行比较,假设我们按照升序的方式进行排序,当左边部分遇到比右边数组部分大的元素的话,那么左边数组部分从这个元素开始到左边部分数组结束的位置是否都大于右边数组的该元素呢?
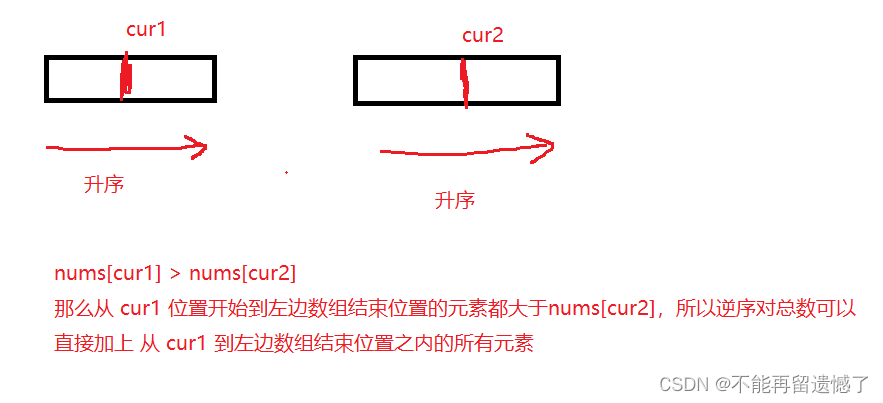
如果nums[cur1] < nums[cur2] 则继续让 cur1 向右移动,直到出现逆序对的情况,这样 cur1 和 cur2 指针都不用返回,就较少了很多的重复比较,使得时间复杂度提升为
O(N*logN)。
2.3 Java代码实现
(1)升序方法
class Solution {int[] tmp;public int reversePairs(int[] nums) {int n = nums.length;tmp = new int[n];return mergeSort(nums,0,n-1);}private int mergeSort(int[] nums, int left, int right) {if(left >= right) return 0;int mid = left + (right - left) / 2;//统计逆序对的数量int ret = 0;//计算左边数组中逆序对的数量ret += mergeSort(nums,left,mid);//计算右边数组中逆序对的数量ret += mergeSort(nums,mid + 1,right);int cur1 = left, cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right) {//当nums[cur1] <= nums[cur2] 的时候,只需要进行合并数组的操作if(nums[cur1] <= nums[cur2]) tmp[i++] = nums[cur1++];//当nums[cur1] > nums[cur2] 的时候,需要更新逆序对的数量,同时也需要合并数组else {ret += mid - cur1 + 1;tmp[i++] = nums[cur2++];}}while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; j++) nums[j] = tmp[j - left];return ret;}
}
(2)降序方法
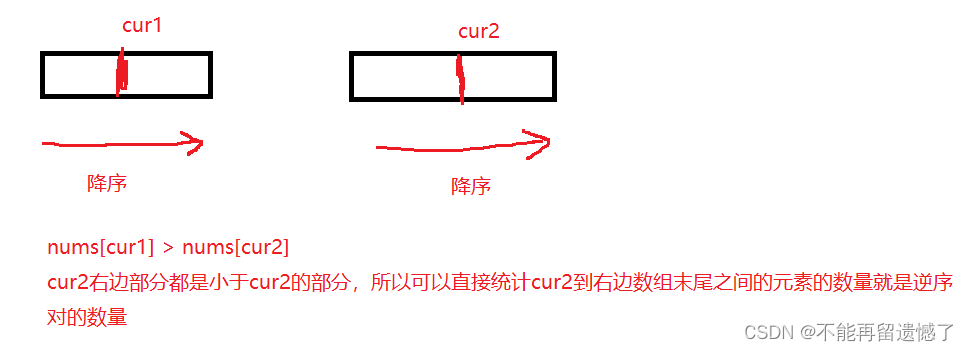
我们也可以用降序排列的方式来实现归并排序,只是当使用降序的时候,需要在右边数组中统计逆序对的数量,因为当遇到 nums[cur1] > nums[cur2] 的时候,如果还是统计左边数组 mid - cur1 + 1 作为逆序对的数量的话,那么当 cur2 向后移动的时候,再遇到 nums[cur1] > nums[cur2] 的时候就会出现重复的情况,所以当我们以降序的方式排序的时候需要在右边数组中统计逆序对的数量。
class Solution {int[] tmp;public int reversePairs(int[] nums) {int n = nums.length;tmp = new int[n];return mergeSort(nums,0,n-1);}private int mergeSort(int[] nums, int left, int right) {if(left >= right) return 0;int mid = left + (right - left) / 2;//统计逆序对的数量int ret = 0;//计算左边数组中逆序对的数量ret += mergeSort(nums,left,mid);//计算右边数组中逆序对的数量ret += mergeSort(nums,mid + 1,right);int cur1 = left, cur2 = mid + 1,i = 0;while(cur1 <= mid && cur2 <= right) {//当nums[cur1] <= nums[cur2] 的时候,只需要进行合并数组的操作if(nums[cur1] <= nums[cur2]) tmp[i++] = nums[cur2++];//当nums[cur1] > nums[cur2] 的时候,需要更新逆序对的数量,同时也需要合并数组else {ret += right - cur2 + 1;tmp[i++] = nums[cur1++];}}while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; j++) nums[j] = tmp[j - left];return ret;}
}
3. 计算右侧小于当前元素的个数
https://leetcode.cn/problems/count-of-smaller-numbers-after-self/description/
3.1 题目要求
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例 1:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
示例 2:
输入:nums = [-1]
输出:[0]
示例 3:
输入:nums = [-1,-1]
输出:[0,0]
提示:
- 1 <= nums.length <= 105
- -104 <= nums[i] <= 104
class Solution {public List<Integer> countSmaller(int[] nums) {}
}
3.2 做题思路
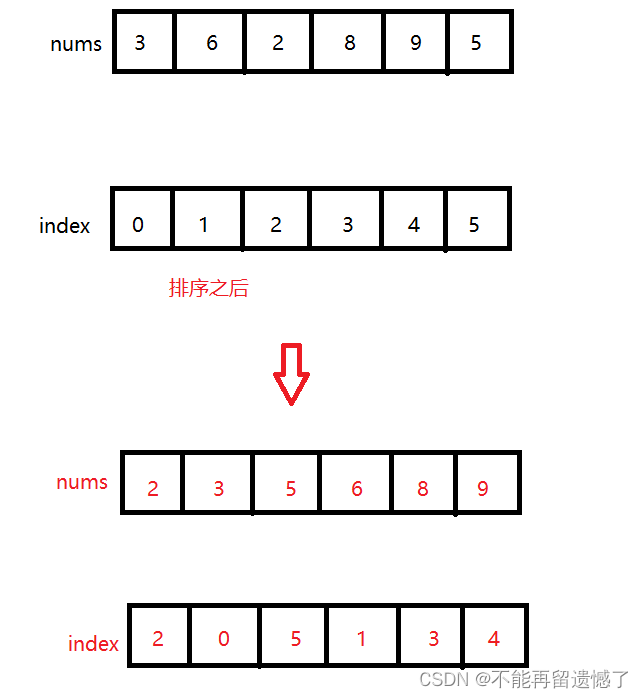
这道题目跟上面的找逆序对的数量是类似的,逆序对是找前面的元素大于后面元素的个数,而这道题是需要找到数组中每个元素的之后的小于该元素的个数,也就是说这个题目返回的是多个数,而不是一个数。那么我们在使用分冶算法的过程中该如何记住对应数字的下标呢?因为在分冶的过程中加上排序,数组中元素的位置是不断变化的,但是这道题目按顺序返回数组中对用位置右边部分大小小于该位置元素的数量,所以这道题目如何记住原本数组对应元素的下标是很重要的。
那么我们如何记住原本数组元素的对应下标呢?我们可以创建一个 index 数组,当数组进行合并排序的时候,相应的 index 数组也跟着变化,这样就能使排序后数组对应位置的 index 数组中存放的是原本数组的下标。
3.3 Java代码实现
class Solution {int[] ret; //该数组中存放右侧小于当前元素的个数int[] index; //存放对应元素的下标int[] tmpNums; //排序后的临时数组int[] tmpIndex; //排序后对应元素的原本下标public List<Integer> countSmaller(int[] nums) {int n = nums.length;ret = new int[n];index = new int[n];//index 数组初始化for(int i = 0; i < n; i++) index[i] = i;tmpNums = new int[n];tmpIndex = new int[n];mergerSort(nums,0,n-1);List<Integer> list = new ArrayList<>();for(int x : ret) list.add(x);return list;}private void mergerSort(int[] nums, int left, int right) {if(left >= right) return;int mid = left + (right - left) / 2;mergerSort(nums,left,mid);mergerSort(nums,mid + 1,right);int cur1 = left, cur2 = mid + 1, i = 0;//降序while(cur1 <= mid && cur2 <= right) {if(nums[cur1] <= nums[cur2]) {tmpNums[i] = nums[cur2];tmpIndex[i++] = index[cur2++];}else {//因为前面的递归中可能出现了右侧小于当前位置的数,所以需要使用+=ret[index[cur1]] += right - cur2 + 1;tmpNums[i] = nums[cur1];tmpIndex[i++] = index[cur1++];}}while(cur1 <= mid) {tmpNums[i] = nums[cur1];tmpIndex[i++] = index[cur1++];}while(cur2 <= right) {tmpNums[i] = nums[cur2];tmpIndex[i++] = index[cur2++];}for(int j = left; j <= right; j++) {nums[j] = tmpNums[j - left];index[j] = tmpIndex[j - left];}}
}
4. 翻转对
https://leetcode.cn/problems/reverse-pairs/description/
4.1 题目要求
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1]
输出: 2
示例 2:
输入: [2,4,3,5,1]
输出: 3
注意:
- 给定数组的长度不会超过50000。
- 输入数组中的所有数字都在32位整数的表示范围内。
class Solution {public int reversePairs(int[] nums) {}
}
4.2 做题思路
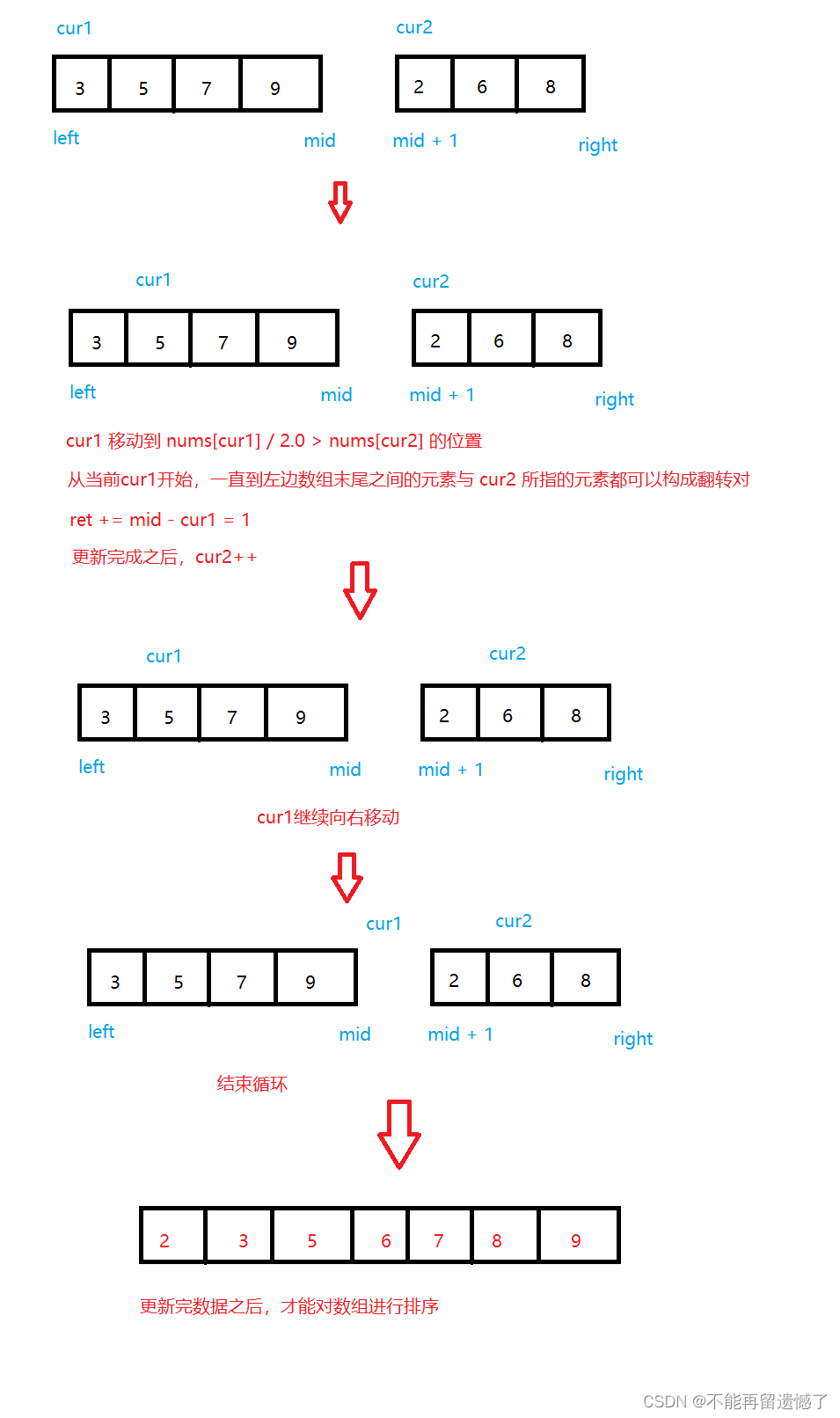
这个题目跟前面的的两个题目都是类似的,只是这里不能在我们更新翻转对的时候就进行排序,因为翻转对的判断条件是 i < j 且 nums[i] > 2*nums[j],根据这个判断条件,我们不能判断出 nums[i] 和 nums[j] 哪个大,所以只能在更新完翻转对之后进行归并排序,其他的步骤基本上是类似的。
4.3 Java代码实现
(1)升序
class Solution {int[] tmp;public int reversePairs(int[] nums) {int n = nums.length;tmp = new int[n];return mergeSort(nums,0,n-1);}private int mergeSort(int[] nums, int left, int right) {if(left >= right) return 0;int ret = 0;int mid = left + (right - left) / 2;//统计左右两部分数组中翻转对的数量ret += mergeSort(nums,left,mid);ret += mergeSort(nums,mid + 1,right);int cur1 = left, cur2 = mid + 1, i = 0;while(cur2 <= right) {//这里需要使用nums[cur1] / 2.0 而不是nums[cur2] * 2,//因为可能会导致溢出while(cur1 <= mid && nums[cur1] / 2.0 <= nums[cur2]) cur1++;if(cur1 > mid) break;ret += mid - cur1 + 1;cur2++;}//升序cur1 = left;cur2 = mid + 1;while(cur1 <= mid && cur2 <= right) {tmp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];}while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; j++) nums[j] = tmp[j - left];return ret;}
}
(2)降序
class Solution {int[] tmp;public int reversePairs(int[] nums) {int n = nums.length;tmp = new int[n];return mergeSort(nums,0,n-1);}private int mergeSort(int[] nums, int left, int right) {if(left >= right) return 0;int ret = 0;int mid = left + (right - left) / 2;ret += mergeSort(nums,left,mid);ret += mergeSort(nums,mid + 1,right);int cur1 = left, cur2 = mid + 1, i = 0;//降序while(cur1 <= mid) {//这里cur1不动,因为cur1向后移动只会越来越小,所以让cur2向后移动while(cur2 <= right && nums[cur1] / 2.0 <= nums[cur2]) cur2++;if(cur2 > right) break;ret += right - cur2 + 1;cur1++;}cur1 = left;cur2 = mid + 1;while(cur1 <= mid && cur2 <= right) {tmp[i++] = nums[cur1] <= nums[cur2] ? nums[cur2++] : nums[cur1++];}while(cur1 <= mid) tmp[i++] = nums[cur1++];while(cur2 <= right) tmp[i++] = nums[cur2++];for(int j = left; j <= right; j++) nums[j] = tmp[j - left];return ret;}
}
总结
归并排序是一种高效而稳定的排序算法,它利用了分治策略,将待排序的数组分解为更小的子数组,并逐步合并这些子数组以获得最终的有序数组。
归并排序算法的核心思想是将待排序数组递归地分解为规模更小、有序的子数组,然后通过合并操作将这些子数组有序地合并成一个大的有序数组。这种分解和合并的过程直到最终合并成排序后的完整数组。
归并排序算法具有以下优点:
-
稳定性:归并排序是一种稳定的排序算法,即相等元素的相对顺序不会被改变。这使得它特别适用于对具有多关键字排序要求的情况。
-
高效性:归并排序的时间复杂度为O(nlogn),其中n是待排序数组的长度。它具有较好的性能表现,并适用于大规模数据的排序。
此外,归并排序算法还具有一定的弹性和灵活性。它可以通过优化合并操作的实现方式,减少额外空间的消耗。此外,归并排序也适用于外部排序,可以处理存储在外部存储介质中的大规模数据。
尽管归并排序算法需要额外的空间和函数调用开销,但由于其稳定性和较好的时间复杂度,它在实际应用中被广泛采用。
相关文章:

【算法系列篇】分治-归并
文章目录 前言什么是归并算法1. 排序数组1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 数组中逆序对2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 计算右侧小于当前元素的个数3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 翻转对4.1 题目要求4.2 做题思路4.3 Java代码实现 总…...
word导出为HTML格式教程,同时也导出图片
在写文档教程时,有时需要借鉴人家的专业文档内容,一般都是word格式文档。word直接复制里面的内容,帐帖到网站编辑器会有很多问题,需要二次清楚下格式才行,而且图片是没办法直接复制到编辑器内的。所以最方便的办法是将…...

事务的优化
例子: 举例:假设我们有一个文件上传的uploadFile方法,在这个方法中我们会先执行上传一个文件到分布式文件系统中的方法addMediaFilesToMinIO( ),上传成功后执行文件资源数据入库的addMediaFilesToDb( ),那么这个时候事务应该加在哪…...
VMware虚拟机安装_新虚拟机创建_CentOS镜像导入_linux指令基本操作
文章目录 1 VMware下载安装1.1 下载网址1.2 安装步骤 2 创建虚拟机与CentOS镜像导入2.1 创建新虚拟机2.2 导入CentOS镜像 3 获取ip与连接Xshell3.1 查看虚拟机ip地址3.2 Xshell使用 1 VMware下载安装 1.1 下载网址 https://www.vmware.com/cn/products/workstation-pro/works…...
Git常用命令用法
参考视频:真的是全能保姆 git、github 保姆级教程入门,工作和协作必备技术,github提交pr - pull request_哔哩哔哩_bilibili 1.Git初始化 首先设置名称和邮箱。然后初始化一下,然后就创建了一个空的Git仓库。 PS D:\golang\oth…...

电子元器件采购的数字化转型:智能采购工具的应用
电子元器件采购的数字化转型是采购领域的一项重要趋势,智能采购工具的应用在此过程中发挥了关键作用。以下是智能采购工具在电子元器件采购数字化转型中的应用方面的一些关键点: 供应链可见性: 智能采购工具可以提供对供应链的实时可见性。通…...
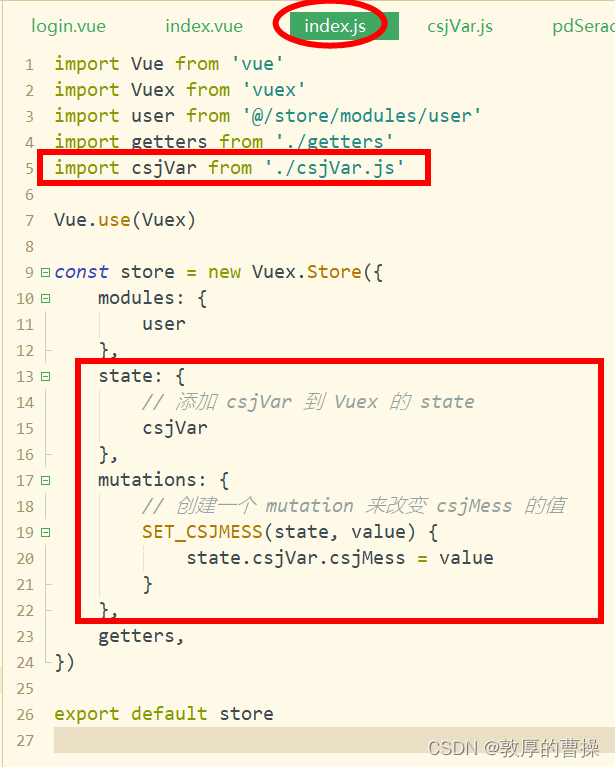
【RuoYi移动端】uni-app中通过vuex的store来实现全局变量的修改和读取
一、在store文件中新建csjVar.js文件 const csjVar {csjMess: [{aaa:"ok"},{bbb:"no"}] } export default csjVar 二、修改store文件中新建index.js文件 import Vue from vue import Vuex from vuex import user from /store/modules/user import gette…...
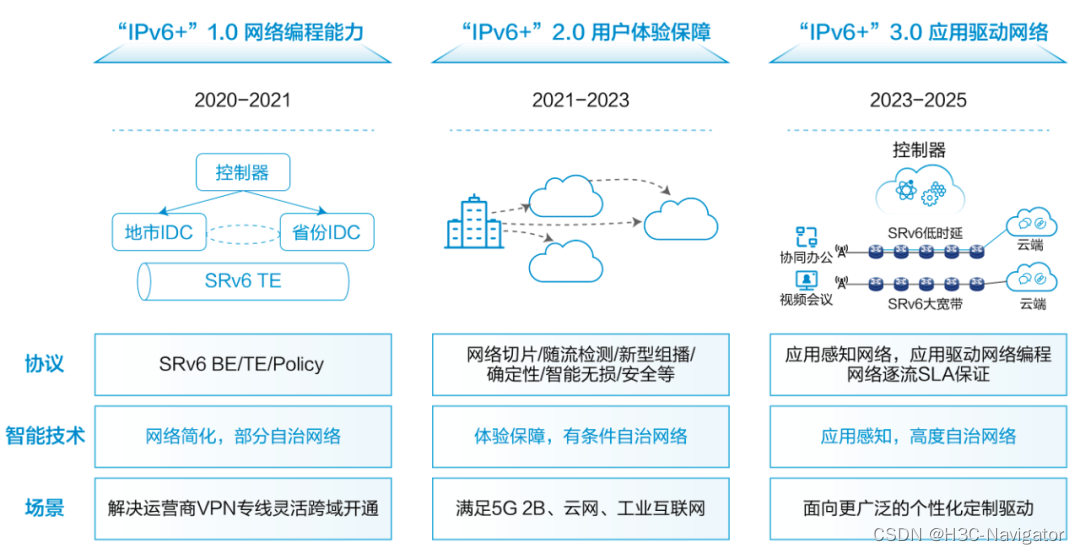
IPv6改造深化之路
01 IPv6改造问题及整体改造思路 随着“十四五”期间国家政策对IPv6深化改造及规模部署的推动,在IPv6改造过程中出现了越来越多的系统性问题,如图1所示。 图1 关于IPv6改造的各种疑问所有跨设备通信的IT软硬件系统均需要处理IP地址,各领域均需…...
,isdigit(),isspace(),round()源码)
atoi(),isdigit(),isspace(),round()源码
atoi()是一个C标准库函数,用于将字符串转换为对应的整数。 以下是atoi()函数的一种简化版本的示例实现: int atoi(const char* str) {int result 0;int sign 1;int i 0;// 处理空格while (isspace(str[i])) {i;}// 处理正负号if (str[i] - || str[…...
)
C# 播放音频文件(播放提示音)
使用SoundPlayer播放声音 System.Media名称空间下的类SoundPlayer 可以让我们很方便的播放wav波形声音文件。SoundPlayer类其实就是对winmm.dll文件中API函数的封装。 首先引入命名空间: using System.Media; SoundPlayer player new SoundPlayer(); player.Sou…...

一种编程语言,
前言:相信看到这篇文章的小伙伴都或多或少有一些编程基础,懂得一些linux的基本命令了吧,本篇文章将带领大家服务器如何部署一个使用django框架开发的一个网站进行云服务器端的部署。 文章使用到的的工具 Python:一种编程语言&…...

云原生Kubernetes:K8S常用服务端口
目录 一、理论 1.K8S常用服务端口号 一、理论 1.K8S常用服务端口号 (1)K8S集群 表1 K8S集群端口 协议端口号K8S集群TCP22使用主机驱动通过SSH进行节点配置TCP53集群DNS服务UDP53集群DNS服务TCP2376主机驱动与Docker守护进程通信的TLS端口TCP2379et…...

clickhouse调优配置
一、官方文档地址 clickhouse的配置项主要在 config.xml 或 users.xml 中, 基本上都在 users.xml 里 config.xml https://clickhouse.tech/docs/en/operations/server-configuration-parameters/settings/ users.xml https://clickhouse.tech/docs/en/operatio…...

pdf文件打开后部分文字无法显示
场景:pdf文件在系统内预览正常,但是下载到本地电脑上,使用wps查看,部分标题会消失,只有标题里面的数字还能显示出来 经过一系列排查,发现查看的电脑上缺失了字体,使用wps查看时,缺失…...

MCS-51单片机温度控制系统的设计
一、项目介绍 注塑机是一种常用的制造设备,用于生产塑料制品。在注塑机的工作过程中,溶胶必须达到一定的温度才能被注入模具中进行成型。因此,在注塑机的生产过程中,温度控制是非常重要的一环。 本项目基于MCS-51单片机设计了一…...
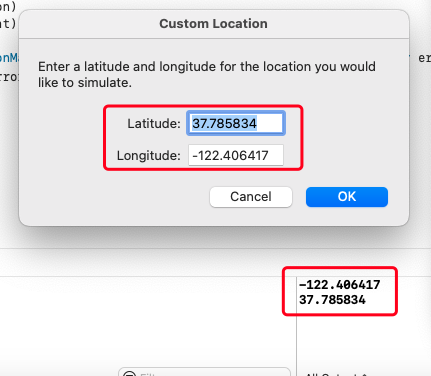
Xcode,swift:Error Domain=kCLErrorDomain Code=1 (null)问题解决
问题描述: iOS开发时,当使用用户的位置权限时,获取用户经纬度报错:Error DomainkCLErrorDomain Code1 "(null)",错误域kCLError域代码1“(null)” 解决方法: 打开模拟机的设置-通用-语言与地区 将地区设置为中国(如果你的开发位置在中国的话) 点击左上方Features,选择…...
0013Java程序设计-springboot教材图文内容审核系统
摘 要目 录第1章 绪论1.1 研究背景与意义1.2 研究内容1.3 论文组成结构 系统实现用户登录模块的实现后台管理系统登录模块的实现投稿信息的实现 开发环境 摘 要 《教材图文内容审核系统》课程案例库研究系统系统主要功能模块包括投稿信息、打卡记录、新闻资讯等,采…...

Unable to remove Temporary User Data
错误截图 原因 项目的临时数据目录是存在了未授权的盘符,当删除它的时候,遇到了权限问题,没有权限没法删除。 解决方法 增加字段:userDataDir 解决...

Rocky(Centos)安装中文字体(防止中文乱码)
1、查看字体列表 运行下列命令 fc-list 若出现,下面截图,则需要安装字体管理软件 安装字体库,运行: yum -y install fontconfig 当看到下图的提示信息时说明已安装成功: 二、添加中文字体 1)window…...
O2OA(翱途)开发平台 V8.1正式发布
尊敬的O2OA(翱途)平台合作伙伴、用户以及亲爱的开发小伙伴们,平台 V8.1版本已正式发布。正值8月的最后一周,我们以更安全、更高效、更好用的崭新面貌迎接9月的到来。 O2OA开发平台v8.1版本更注重于对系统级别的安全防护。其中重大的更新,是对…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
