【管理运筹学】第 7 章 | 图与网络分析(1,图论背景以及基本概念、术语、矩阵表示)
文章目录
- 引言
- 一、图与网络的基本知识
- 1.1 图与网络的基本概念
- 1.1.1 图的定义
- 1.1.2 图中相关术语
- 1.1.3 一些特殊图类
- 1.1.4 图的运算
- 1.2 图的矩阵表示
- 1.2.1 邻接矩阵
- 1.2.2 可达矩阵
- 1.2.3 关联矩阵
- 1.2.4 权矩阵
- 写在最后
引言
按照正常进度应该学习动态规划了,但我想换换口味,而且动态规划听说也有一定难度,还不一定会考。
先说说图论的一些背景知识和发展情况吧。
图论是几十年来发展迅速、应用广泛的一个新的数学分支。它与数学的其他分支如矩阵论、概率论、数值分析等都有着密切地联系。事实上,图论为任何一个包含了一种二元关系的系统提供了一个数学模型;也因为它使用了图解式的表示法,图就具有了一种直观的和符合美学的外形。
图论的发展大致分为 3 个阶段。

第一阶段是从 18 世纪中叶到 19 世纪中叶,称为萌芽期。起源是“七桥游戏”问题,如下图所示。

问题是:能否从这四块陆地中的任何一块开始,通过每一座桥一次,并且仅一次,再次回到起点。
瑞士数学家欧拉(Euler)就这一问题发表了图论的第一篇论文,证明了不存在七桥游戏问题的解,并且把这个问题(边一笔画问题)深入一步地一般化了,给出了一个图存在欧拉圈的判定法则。
自从中国邮递员问题(Chinese Postman Problem)提出来以后,欧拉问题才具有了强烈的实用价值。
中国邮递员问题是这样的:邮递员在沿着邮路出发前,必须先从邮局取走他所应分发的邮件。为了节约时间,每一位邮递员都愿意以尽可能少的行程走完他所必须走的所有路线。用图论的话来说,是指如何以尽可能少的行程遍历邮路上所有各条街道后又回到他的出发点。
这类问题的第一篇论文是由中国数学家、山东师范大学的管梅谷教授在 1962 年提出的,因而得名“中国邮递员问题”。

19 世纪中叶到 20 世纪中叶是图论发展的第二阶段,这一时期图论大量问题涌现,其中以 Hamilton 问题和四色猜想最为著名。
1856 年英国数学家 William Hamilton 爵士发明了“绕行世界”的游戏。这个游戏用一个规则十二面体,它的 20 个顶点标以 20 个城市的名字,要求游戏者找一条从某一城市出发的路线,它经过每个城市恰好一次,并且最终回到出发点。
将正十二面体投影到平面上,就得到了下图。

实际上 Hamilton 周游世界问题,是图论中的点一笔画问题,是要在上图中找具有以下两个特点的一个圈 H H H :1.图中的每一个顶点都在圈 H H H 中出现;2.在 H H H 中顶点不重复出现(起终点不算重复)。这个圈称为 Hamilton 圈。
四色猜想问题,即能否仅用 4 种颜色给地图染色,使得相邻国家有不同的颜色。用图来描述就是:用点来表示国家,两个国家若有公共边界,就用一条边将这两点连接起来,于是,四色猜想问题就转化为能否用四种颜色给平面的点染色,使得相邻的点有不同颜色。

20 世纪中叶以后,是图论发展的第三个阶段,这一时期图论经过爆炸性的发展,成长为一门独立学科。其中最重要的是:出现了研究问题和解决问题的强有力工具:计算机。
一、图与网络的基本知识
1.1 图与网络的基本概念
1.1.1 图的定义
自然界和人类社会中,大量的事物及事物之间的关系,常可以用图形来描述。常将所研究对象看成一个点,用连线(带箭头或者不带箭头)表示对象之间的某种特定关系。为了区别起见,我们称不带箭头连线称为边,带箭头的连线称为弧。
定义 1.1 —— 一个图是由一个非空集合 V V V ,以及 V V V 中元素的无序(或有序)点对组成的集合 E E E (或 A A A)所组成。 V V V 中元素的无序点对所构成的集合称为边集合 E E E ,由点集合 V V V 和边集合 E E E 构成的图称为无向图(简称图),记作 G = ( V , E ) G=(V,E) G=(V,E) 。一条连接点 v i , v j v_i,v_j vi,vj 的边 e i j e_{ij} eij ,记为 e i j = [ v i , v j ] e_{ij}=[v_i,v_j] eij=[vi,vj] 或 e i j = [ v j , v i ] e_{ij}=[v_j,v_i] eij=[vj,vi] 。 V V V 中元素的有序点对构成的集合称为弧集合 A A A ,由点集合 V V V 和弧集合 A A A 构成的图为有向图,记为 D = ( V , A ) D=(V,A) D=(V,A) 。一条方向是从 v i v_i vi 指向 v j v_j vj 的弧记为 a i j = ( v i , v j ) a_{ij}=(v_i,v_j) aij=(vi,vj) 。

若图 G G G 中,某个边的两个端点相同,称该边为环,若两个点之间有多于一条的边,称为多重边。一个无环、无多重边的图称为简单图,无环但允许有多重边的图称为多重图。
图 G G G 或 D D D 中的点数记为 n = ∣ V ∣ n=|V| n=∣V∣ ,边(弧)数记为 m = ∣ E ∣ ( m = ∣ A ∣ ) m=|E| (m=|A|) m=∣E∣(m=∣A∣) ,在不引起混乱的情况下,分别简记为 n , m n,m n,m ,其中 n n n 为图的阶,若 n n n 为有限的,称为有限阶。
1.1.2 图中相关术语
- 端点。当 e i j = [ v i , v j ] e_{ij}=[v_i,v_j] eij=[vi,vj] 时,与边 e i j e_{ij} eij 相连的顶点称为边 e i j e_{ij} eij 的端点。
- 边与点相关联。当 e i j = [ v i , v j ] e_{ij}=[v_i,v_j] eij=[vi,vj] 时, e i j e_{ij} eij 与 v i , v j v_i,v_j vi,vj 称为边顶相关联。
- 邻点。
- 邻边。
- 环。只与一个顶点相关联的边称为环。
- 平行边。具有相同的两个端点的边称为平行边。
- 邻域。与某点相邻接的点的集合。
- 次。以点 v i v_i vi 为端点的边的数目称为点 v i v_i vi 在 G G G 中的次,记为: d ( v i ) d(v_i) d(vi) 。
如果有环,则按两条边记,即 d ( v i ) = d l ( v i ) + 2 l ( v i ) d(v_i)=d_l(v_i)+2l(v_i) d(vi)=dl(vi)+2l(vi) 其中: d l ( v i ) d_l(v_i) dl(vi) 是与 v i v_i vi 相关联的非环边数, l ( v i ) l(v_i) l(vi) 是与 v i v_i vi 相关联的环数。 - 次序列。若 V = { v 1 , v 2 , … , v p } V=\{v_1,v_2,\dots,v_p\} V={v1,v2,…,vp} ,则相对于每个点都有一个次,则可以得到一个次序列 ( d ( v 1 ) , d ( v 2 ) , … ) (d(v_1),d(v_2),\dots) (d(v1),d(v2),…) 。
定理 1.1 —— 对于图 G = ( V , E ) G=(V,E) G=(V,E) ,其中 ∣ V ∣ = n , ∣ E ∣ = m |V|=n,|E|=m ∣V∣=n,∣E∣=m ,则有: ∑ v ∈ V d ( v ) = 2 m \sum_{v \in V}d(v)=2m v∈V∑d(v)=2m 定理 1.2 —— 奇数次顶点的总数是偶数。
- 悬点。次为 1 的点。
- 悬边。悬点关联的边。
- 孤立点。次为 0 的点。
- 链。
- 初等链。链 Q Q Q 中的顶点均不相同。
- 简单链。链中边都不相同。
- 链的长度。为所包含的边数。
- 圈。
- 路。
- 路径。有向图中路每个顶点均不相同称为路径。
- 回路。路的第一个点和最后一个点相同。
1.1.3 一些特殊图类
- 平凡图。节点数 n = 1 n=1 n=1 ,边数 m = 0 m=0 m=0 的图。
- 零图。边数 m = 0 m=0 m=0 。
- 连通图。图中每对节点都有一条链(路)连接,称这个图是连通的。
- 树。无圈的连通图。
- 完备图。任意两个顶点之间恰有一条边相关联。
- 二分图。
- 完全二分图。
- 正则图。每个点的次数均相同。
- 有向网络。加权的有向图。
1.1.4 图的运算
(1)子图和支撑
子图、支撑子图都是图 G G G 的点或边作删除运算得到的。子图点和边都是原图的子集,支撑子图点和原图一样,边是原图子集。
(2)图的收缩运算
(3)割集
常记为 Φ ( X ) \varPhi(X) Φ(X) ,如下图中,若 X = { V 1 } X=\{V_1\} X={V1} ,则割集为 Φ ( X ) = { [ v 1 , v 2 ] , [ v 1 , v 3 ] , [ v 1 , v 4 } \varPhi(X)=\{[v_1,v_2],[v_1,v_3],[v_1,v_4\} Φ(X)={[v1,v2],[v1,v3],[v1,v4} 。即用一条线去割,要求可以将 X X X 完整割出来,这条线碰着的边记为割集。

(4)图的同构
设 G 1 , G 2 G_1,G_2 G1,G2 为两个同阶图,若顶点集合 V 1 , V 2 V_1,V_2 V1,V2 以及边集合 E 1 , E 2 E_1,E_2 E1,E2 之间在保持关联性质条件下一一对应,则称图 G 1 , G 2 G_1,G_2 G1,G2 同构。如下图所示。

1.2 图的矩阵表示
为了方便利用计算机识别图的相关信息,我们通过矩阵表示法来表示一个图,主要有邻接矩阵、关联矩阵、可达矩阵、权矩阵等。
1.2.1 邻接矩阵
邻接矩阵用于描述两个顶点之间是否有边(弧)相连。若两点之间有边(弧)相连,对应矩阵元素为 1 ,否则对应矩阵元素为 0 。
显然,无向图的邻接矩阵是一个关于对角线对称的矩阵。

1.2.2 可达矩阵
在有向图中可达矩阵用于描述两点之间是否有路相连,若有路相连,对应矩阵元素为 1 ,否则为 0 。
1.2.3 关联矩阵
有向图的关联矩阵也称为顶点—边关联矩阵。其每一行表示一个点 v i v_i vi ,每一列表示一条弧 a j a_j aj ,若 v i v_i vi 是弧 a j a_j aj 的起点,则对应矩阵元素 m i j = 1 m_{ij}=1 mij=1 ;若为弧的终点,记为 -1 ,无关则记为 0 。
1.2.4 权矩阵
可以理解为邻接矩阵的延伸,当两点之间存在边或弧时,对应矩阵元素为该边或弧的权重;当两点之间无边时,对应元素为 ∞ \infty ∞ ;权矩阵对角元素全为 0 。
写在最后
这概念可是真的多,不过结合图来理解就还好,后面我们就来说说图论中的一些经典问题。
相关文章:

【管理运筹学】第 7 章 | 图与网络分析(1,图论背景以及基本概念、术语、矩阵表示)
文章目录 引言一、图与网络的基本知识1.1 图与网络的基本概念1.1.1 图的定义1.1.2 图中相关术语1.1.3 一些特殊图类1.1.4 图的运算 1.2 图的矩阵表示1.2.1 邻接矩阵1.2.2 可达矩阵1.2.3 关联矩阵1.2.4 权矩阵 写在最后 引言 按照正常进度应该学习动态规划了,但我想…...

支持CAN FD的Kvaser PCIEcan 4xCAN v2编码: 73-30130-01414-5如何应用?
这里是引用 Kvaser PCIEcan 4xCAN v2(编码: 73-30130-01414-5)是一款小巧而先进的多通道实时CAN接口,可发送和接收CAN总线上的标准和扩展CAN消息,时间戳精度高。其与所有使用Kvaser CANlib的应用程序兼容。 主要特性 PCI Express…...

经济2023---风口
改革开放以来,中国共有12次比较好的阶级跃迁的机会: 包括80年代选部委院校、办乡镇企业、倒卖商品;90年代下海、选外语外贸、炒股;00年代从事资源品行业、选金融、炒房;10年代选计算机、搞互联网、买比特币。 从这里…...

JWFD开源工作流-矩阵引擎设计-高维向量空间分析法
JWFD开源工作流-矩阵引擎设计-高维向量空间分析法 在把已知的流程节点查找到之后,输出下标,但是我们发现,还有一些节点并未被 探测到,遍历并没有完全的完成,仍然有泄露的节点在其中,这个问题…...

WIN10访问Ubuntu的Samba
WIN10访问Ubuntu的Samba 在Ubuntu中安装好Samba后,如果无法在Win10里访问共享目录或者无法进行写操作,可以进行如下检查: 检查用户是否添加到共享和共享组 $ sudo adduser yourname sambashare 可以编辑:,查看文件/etc…...

AbstractExecutorService 抽象类
java.util.concurrent.AbstractExecutorService 是 Java 并发编程中的一个抽象类,它定义了 ExecutorService 接口的基本行为。ExecutorService 是一个接口,它提供了一种以异步方式执行任务的方法。 AbstractExecutorService 类包含以下一些重要的方法: void execute(Runnab…...

Android12 ethernet和wifi共存
1.修改网络优先走wifi packages/modules/Connectivity/service/src/com/android/server/connectivity/NetworkRanker.java -44,7 44,7 import java.util.Arrays;import java.util.Collection;import java.util.List;import java.util.function.Predicate; - import andro…...
记录使用layui弹窗实现签名、签字
一、前言 本来项目使用的是OCX方式做签字的,因为项目需要转到国产化,不在支持OCX方式,需要使用前端进行签字操作 注:有啥问题看看文档,或者换着思路来,本文仅供参考! 二、使用组件 获取jSign…...
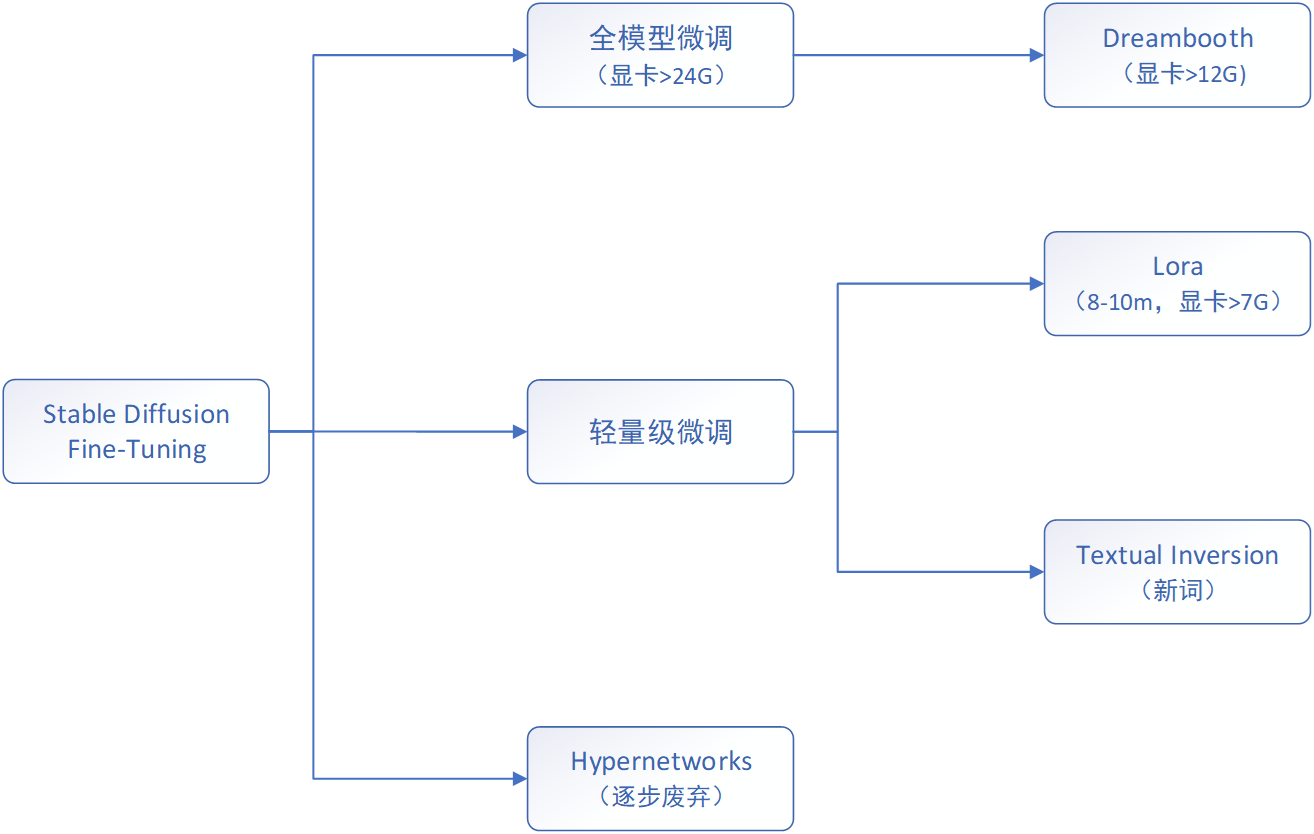
【AIGC系列】Stable Diffusion 小白快速入门课程大纲
一、前言 本文是《Stable Diffusion 从入门到企业级应用实战》系列课程的前置学习引导部分,《Stable Diffusion新手完整学习地图课程》的课程大纲。该课程主要的培训对象是: 没有人工智能背景,想快速上手Stable Diffusion的初学者;想掌握St…...
在kali环境下安装Beef-Xss靶场搭建
目录 一、更新安装包 二、安装beef-xss 三、启动Beef-Xss工具 1、查看hook.js 2、查看后台登录地址 3、查看用户名和登录密码 4、登录页面 5、点击 Hook me:将配置的页面导入BEEF中 一、更新安装包 ┌──(root㉿kali)-[/home/kali] └─# apt-get update 二、安装be…...

【Apollo】自动驾驶技术的介绍
阿波罗是百度发布的名为“Apollo(阿波罗)”的向汽车行业及自动驾驶领域的合作伙伴提供的软件平台。 帮助汽车行业及自动驾驶领域的合作伙伴结合车辆和硬件系统,快速搭建一套属于自己的自动驾驶系统。 百度开放此项计划旨在建立一个以合作为中…...
HTML emoji整理 表情符号
<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><title>测试</title></head><body><div style"font-size: 50px;">🔔</div><script>let count 0d…...
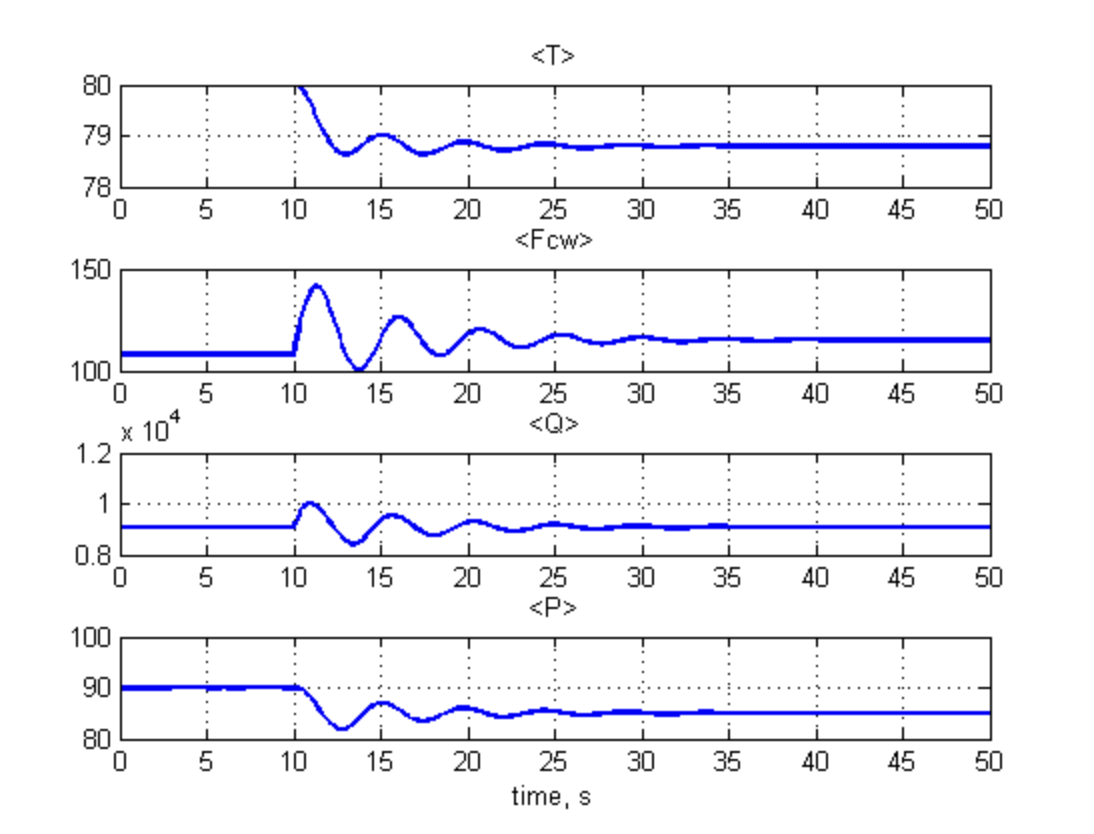
【蒸汽冷凝器型号和PI控制】具有PID控制的蒸汽冷凝器的动力学模型(MatlabSimulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

mall :hutool项目源码解析
文章目录 一、mall开源项目1.1 来源1.2 项目转移1.3 项目克隆 二、Hutool工具类库2.1 Hutool 简介 三、源码解析3.1 集成与配置3.1.1 导入依赖3.1.2 添加配置 3.2 核心工具类3.2.1 AnnotationUtil使用:注解工具类3.2.2 BeanUtil使用:JavaBean的工具类3.2…...

【网络编程】TCP传输控制协议(Transmission Control Protocol)
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...

云原生Kubernetes:kubectl管理命令
目录 一、理论 1.kubectl 管理命令 2.项目的生命周期 二、实验 1.kubectl 管理命令 2.项目的生命周期 三、总结 一、理论 1.kubectl 管理命令 (1)陈述式资源管理方法 kubernetes集群管理集群资源的唯一入口是通过相应的方法调用apiserver的接口…...
)
前端面试的话术集锦第 5 篇:高频考点( 类型转换 深浅拷贝 模块化机制等)
这是记录前端面试的话术集锦第五篇博文——高频考点(类型转换 & 深浅拷贝 & 模块化机制等),我会不断更新该博文。❗❗❗ 1. typeof类型判断: typeof是否能正确判断类型? instanceof能正确判断对象的原理是什么 typeof对于原始类型来说,除了null都可以显示正确的类…...

微服务·架构组件之网关
微服务架构组件之网关 引言 微服务架构已成为构建大型和复杂应用程序的流行范式之一。在微服务架构中,通常一个系统会被拆分为多个微服务,如果 客户端多次请求不同的微服务,会增加客户端代码和配置的复杂性,维护成本比较高。每…...

Google 开源库Guava详解
一、概述 Guava是一组来自Google的核心Java库,包括新的集合类型(如多映射和多集)、不可变集合、图库和并发、I/O、哈希、原语、字符串等实用程序!它广泛用于Google中的大多数Java项目,也被许多其他公司广泛使用。 Gua…...

ISP——3A算法
目录 前沿一. 自动曝光AE1.1. 自动曝光1.2. 18%灰1.3. 测光区域1.4. 摄影曝光加法系统1.5. AE算法1.5.1. 考虑事项1.5.2. AE实现过程 1.6. AE算法 二. 自动对焦AF2.1. 什么是自动对焦2.2. 图像清晰度评价方法2.2.1. Brenner 梯度函数2.2.2. Tenengrad 梯度函数2.2.3. Laplacian…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
