2023年高教社杯数学建模思路 - 案例:最短时间生产计划安排
文章目录
- 0 赛题思路
- 1 模型描述
- 2 实例
- 2.1 问题描述
- 2.2 数学模型
- 2.2.1 模型流程
- 2.2.2 符号约定
- 2.2.3 求解模型
- 2.3 相关代码
- 2.4 模型求解结果
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
最短时间生产计划模型
该模型出现在好几个竞赛赛题上,预测2023今年国赛也会与该模型相关。
1 模型描述
离散系统仿真在工业生产的工序安排中起到了相当重要的作用,如何就一些内部机制复杂的离散问题建立简单易行、可监测性强的数学模型一直是仿真技术的研究热点.
离散事件系统现有三种仿真建模策略,即:
- 事件调度法
- 活动扫描法
- 进程交互法.
该模型demo学长采用了其中的活动扫描法对生产中的一个实际例子进行了处理.
活动扫描法对于各事件之间相关性很强的系统有着很好的适用性.
2 实例
2.1 问题描述
在许多工厂生产过程中,由于设备的数量、产品加工的次序限制,往往不能简单地安排生产任务.我们设想,应用强大的数学软件配合简单易行的方法进行安排.
设某重型机械厂产品都是单件性的,其中有一车间共有4种不同设备,现接受6件产品的加工任务,每件产品接受的程序在指定的设备上加工,其工序与加工周期如下表

现在我们根据这一实际问题,寻求安排的方法.
要求:
1、每件产品必须按规定的工序加工,不得颠倒.
2、每台设备在同一时间只能担任一项任务(每件产品的每个工序为一个任务).
3、在尽可能短的时间里,完成所接受的全部任务.
为了节省电能,合理分配生产任务,厂方还要求:
1、做出每件产品的每个工序开工、完工时间表.
2、给出每台设备承担任务的时间表.
2.2 数学模型
2.2.1 模型流程

2.2.2 符号约定

2.2.3 求解模型
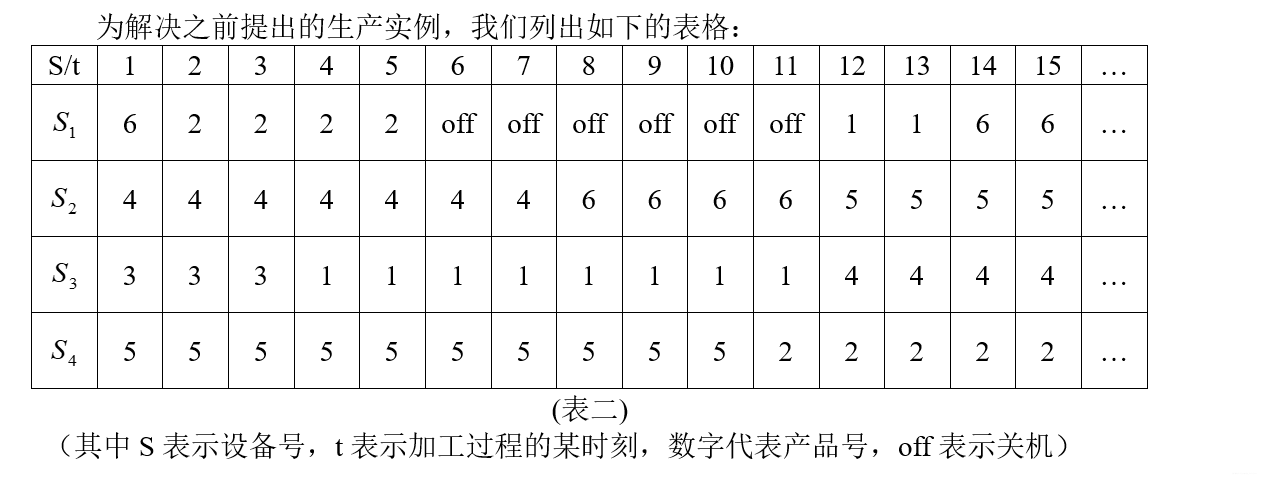
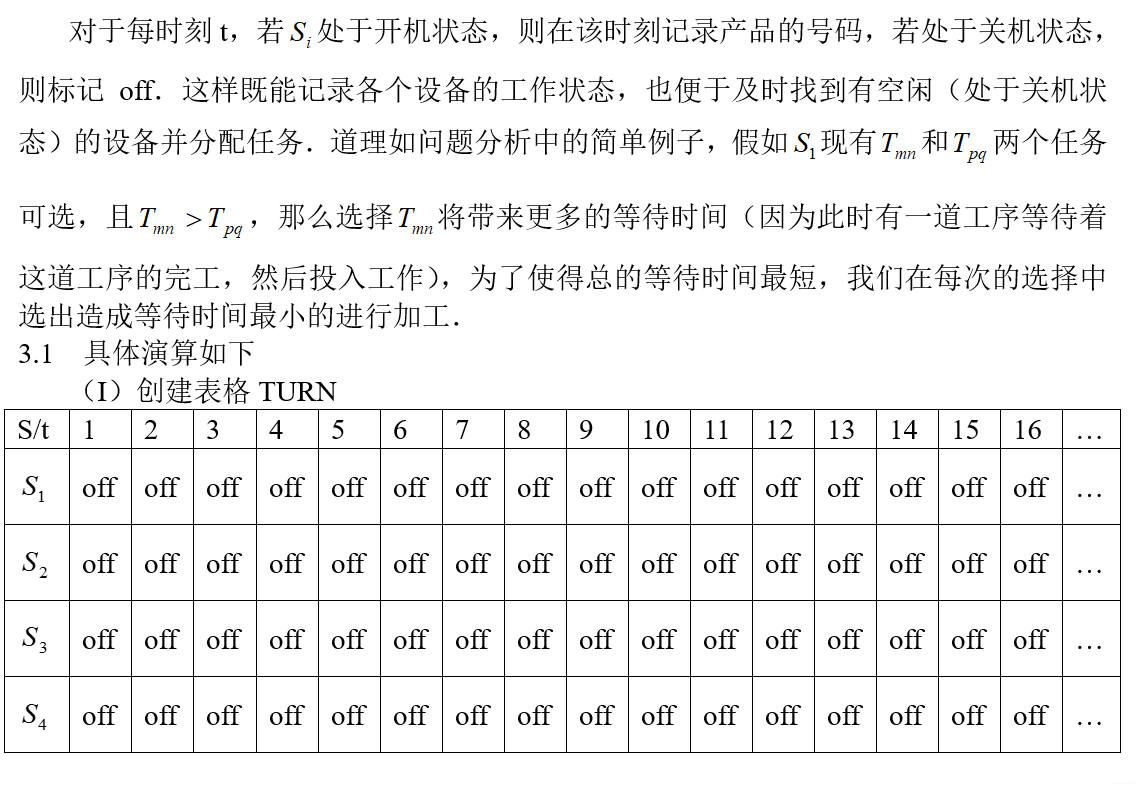
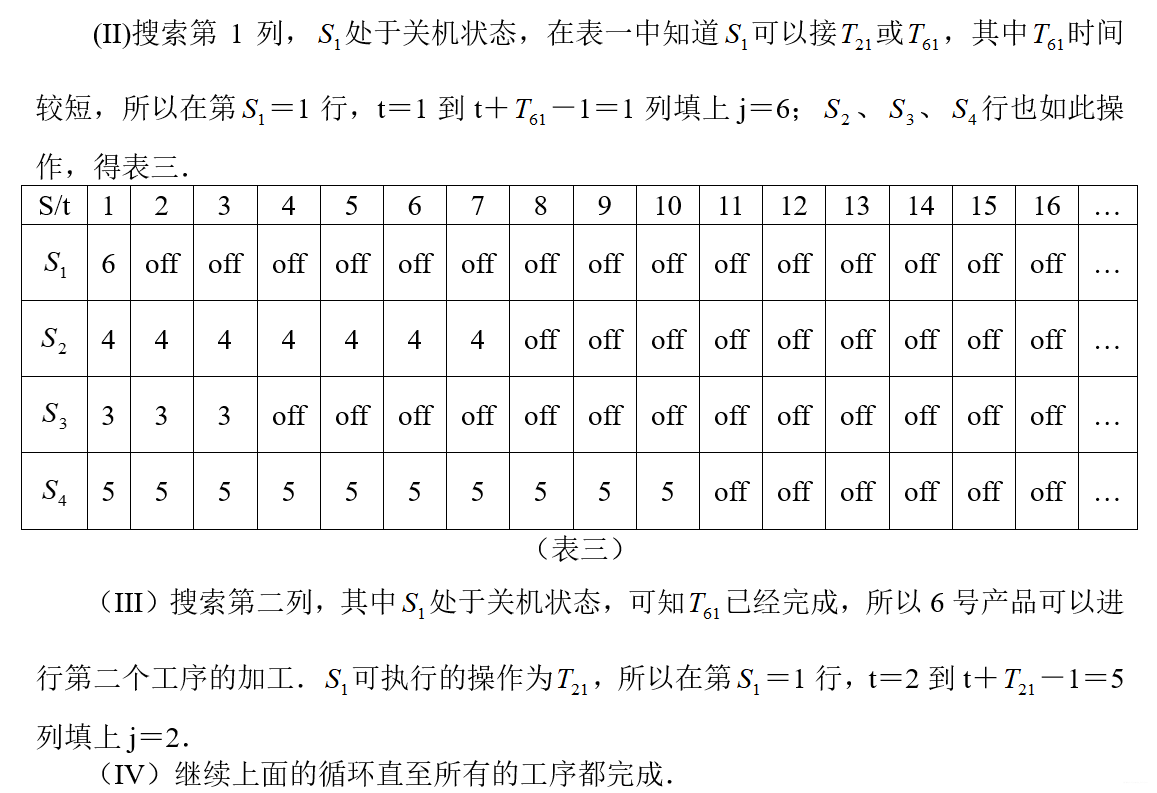
2.3 相关代码
clear
clc
seq=[3 1 2 3 4 0 0 0 %各产品加工时所用的设备的次序1 4 2 3 0 0 0 03 4 1 2 1 0 0 02 3 4 1 4 3 0 04 2 3 4 1 3 4 01 2 1 3 4 1 3 1];tim=[8 2 4 24 6 0 0 0 %加工对应使用的时间4 5 3 4 0 0 0 03 7 15 20 8 0 0 07 6 21 1 16 3 0 010 4 8 4 12 6 1 01 4 7 3 5 2 5 8];
whole=[0 0 0 0];
for i=1:6for j=1:8if(seq(i,j)~=0)whole(seq(i,j))=whole(seq(i,j))+tim(i,j);endend
end
whole %生产各件产品所需的总时间mes=cell(4,1); %记录各个设备的工作时间(对应于上面tim的位置)
for k=1:4mes{k,1}=zeros(6,8);for j=1:8for i=1:6if(seq(i,j)==k)mes{k,1}(i,j)=tim(i,j);elsemes{k,1}(i,j)=100;endendend
endturn=cell(5,100); %记录四个设备的开关时间及加工对象(on(i))
for i=1:4for j=1:100turn{i,j}='off';end
end
for i=1:100turn{5,i}=[num2str(i) '分'];
endopen=zeros(6,8);
%记录6个产品的加工进度,0表示未进行,1表示已开始(或已结束),2表示可选,3表示没有这个程序
for i=1:6open(i,1)=2;
end
for i=1:6for j=1:8if seq(i,j)==0open(i,j)=3;endend
endgongxu=zeros(6,1);
dai=zeros(4,1);
j=1;
s=[1 1 1 1 1 3 3 3
1 1 1 1 3 3 3 3
1 1 1 1 1 3 3 3
1 1 1 1 1 1 3 3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1];
while isequal(open,s)==0on=[];for i=1:4if turn{i,j}=='off'
%在turn矩阵中逐列搜索,若设备处于关机状态,则作记录(可用)on=[on i];endendl1=length(on);for m=1:l1 %在整个生产计划中(对设备逐个)寻找能够选作操作的步骤[x,y]=find(open==2);l2=length(x);a=[x(1) y(1)];for k=1:l2 %对某个设备on(m),找出当前它能操作的步骤中耗时最小的一个if mes{on(m)}(a(1),a(2))>mes{on(m)}(x(k),y(k))a=[x(k) y(k)];endendif turn{on(m),j}=='off' & mes{on(m)}(a(1),a(2))~=100
%若时间为100则意味着这个步骤不属于我们希望使用的那件设备while tim(a(1),a(2))>0turn{on(m),tim(a(1),a(2))+j-1}=a(1);tim(a(1),a(2))=tim(a(1),a(2))-1;endendendfor i=1:4if turn{i,j}~='off'dai(i)=turn{i,j};endendfor i=1:4if turn{i,j}~='off' & turn{i,j+1}=='off'gongxu(turn{i,j})=gongxu(turn{i,j})+1;open(turn{i,j},gongxu(turn{i,j}))=1;endif gongxu(dai(i))<8 & open(dai(i),gongxu(dai(i))+1)~=3 & turn{i,j+1}=='off'open(dai(i),gongxu(dai(i))+1)=2;endendj=j+1;
end2.4 模型求解结果
每件产品的每个工序开工、完工时间表

每台设备承担任务的时间表
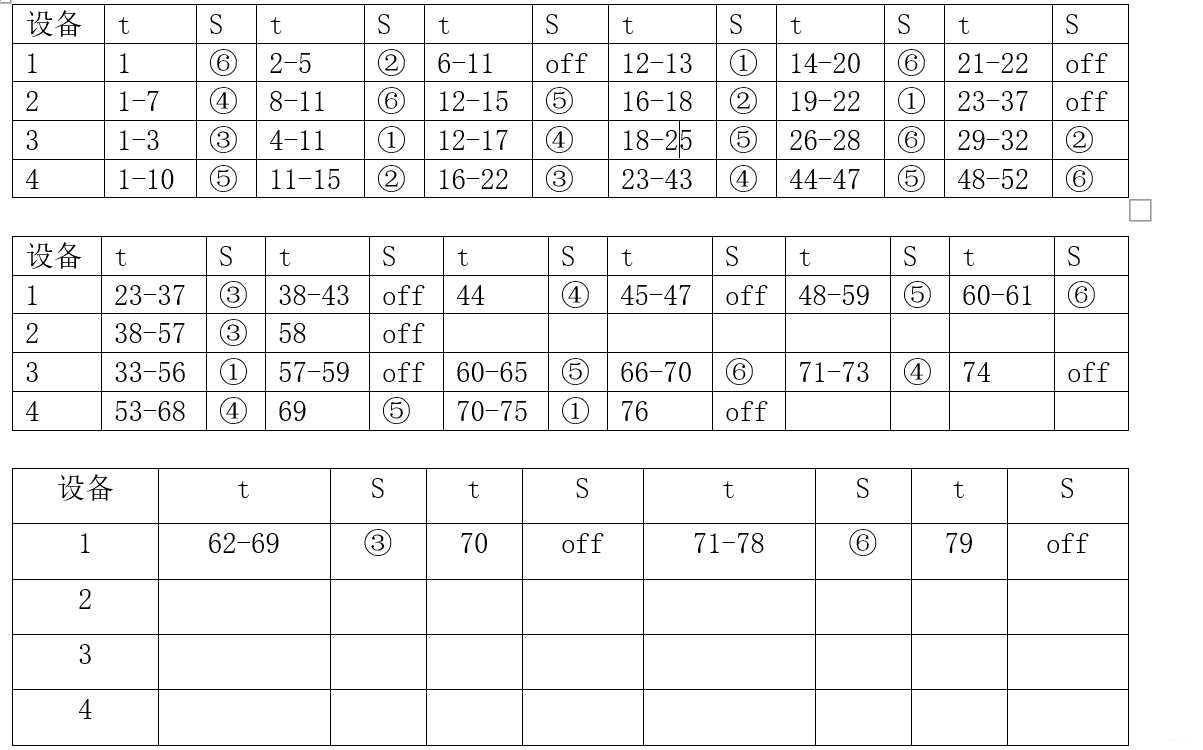
从结果中我们可以看到,使用这种方法,只需78个单位时间就可以完成所有的工序.而我们同时也可以在论文的开始部分看到,单就完成 就需耗费75个单位时间.可见这种方法得出的结果还是相当使人满意的,而且操作简单,可监测性强.
建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯数学建模思路 - 案例:最短时间生产计划安排
文章目录 0 赛题思路1 模型描述2 实例2.1 问题描述2.2 数学模型2.2.1 模型流程2.2.2 符号约定2.2.3 求解模型 2.3 相关代码2.4 模型求解结果 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 最短时…...
)
算法工程题(二叉树递归)
* 题意说明: * 给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 * 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。 * * 示例 1: * 输入:p [1,2,3]…...

“指针跃动”受邀参加全球贸易服务峰会
“指针跃动”受邀参加全球贸易服务峰会 有“服”同享 共赢未来 引子 在全球化日益盛行的今天,贸易不再仅仅是物质的交流,更涉及到服务、理念、文化和科技的共享。中国国际服务贸易交易会全球贸易服务峰会,就是这个趋势的集中体现。在这次峰会…...

Go Web开发的高级技巧和最佳实践
Go Web开发的高级技巧和最佳实践 欢迎来到Go语言Web开发的高级技巧和最佳实践指南。在这篇文章中,我们将深入探讨Go语言Web应用程序的高级主题,包括性能优化、安全性、部署和微服务架构。 性能优化 性能是Web应用程序的关键因素之一。Go语言以其出色的…...
Verilog 基础知识
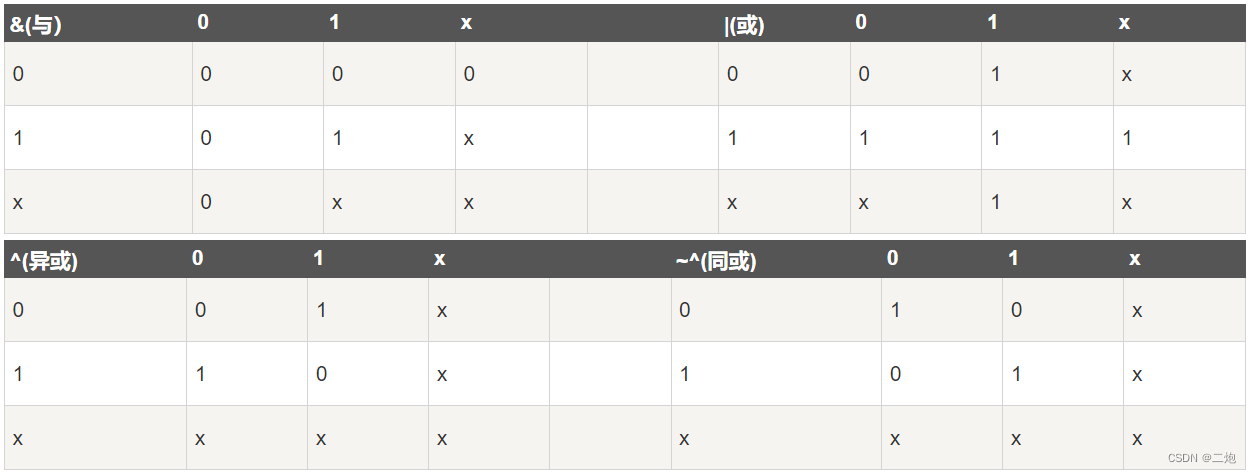
1、数值种类 Verilog HDL 有下列四种基本的值来表示硬件电路中的电平逻辑: 0:逻辑 0 或 “假”1:逻辑 1 或 “真”x 或 X:未知 x 意味着信号数值的不确定,即在实际电路里,信号可能为 1,也可能…...

element ui 表格组件与分页组件的二次封装
目录 组件封装 parseTime函数 debounce 函数 页面使用 【扩展】vue 函数式组件 函数式组件特点: 函数式组件的优点: 【扩展】vue中的render函数 一、初步认识render函数 二、为什么使用render函数 三、render函数的解析 组件封装 这段代码是一…...

递归算法学习——有效的数独,解数独
一,有效的数独 1.题意 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&#x…...
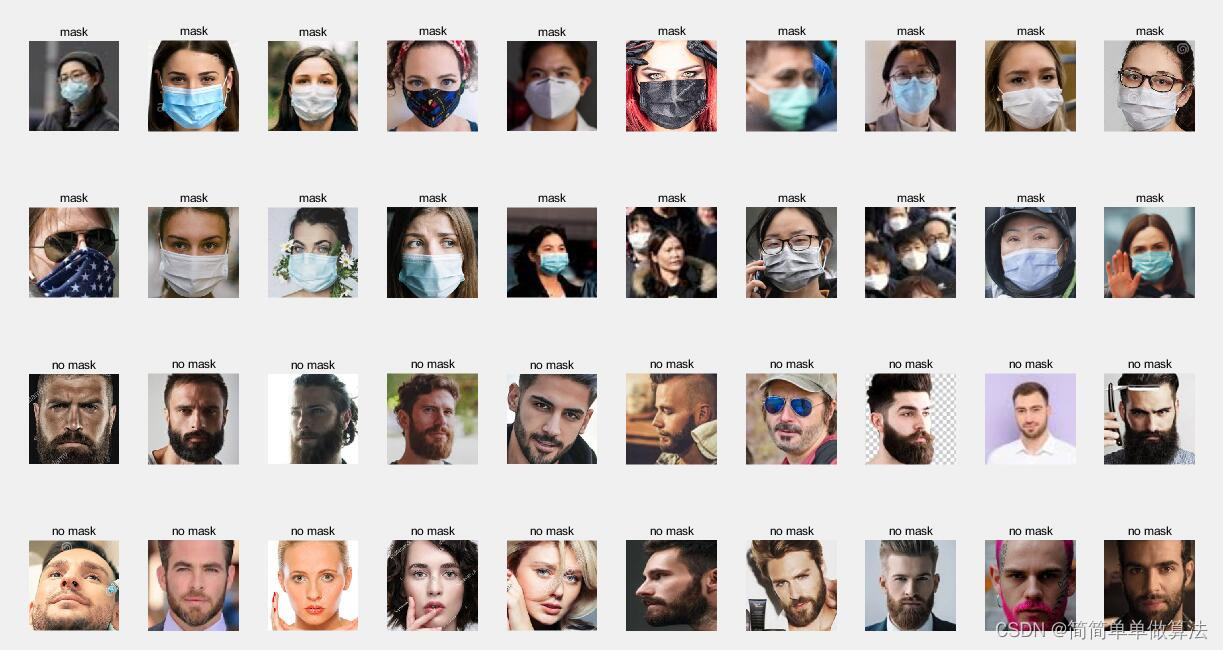
基于Alexnet深度学习网络的人员口罩识别算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 file_path1 test\mask\;% 图像文件夹路径 %获取测试图像文件夹下所有jpg格式的图像文件…...

【Java Web】利用Spring整合Redis,配置RedisTemplate
1. 在config中加入RedisConfig配置类 package com.nowcoder.community.config;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.data.redis.connection.RedisConnectionFacto…...

如何正确的写出第一个java程序:hello java
1 前言 最近公司由于项目需要,开始撸java代码了。学习一门新的编程语言,刚开始总是要踩很多坑,所以记录一下学习过程,也希望对java初学者有所帮助。 2 hello java 2.1 程序源码 程序内容十分简单,这里就不再过多赘…...
)
使用llvm 编译最新的linux 内核(LoongArch)
1. 准备交叉工具链 llvm 使用了最新的llvm-17, 编译方法见:编译LoongArch的llvm交叉工具链 gcc 从linux 官方下载:http://mirrors.edge.kernel.org/pub/tools/crosstool/files/bin/x86_64/13.2.0/x86_64-gcc-13.2.0-nolibc-loongarch64-linux.tar.xz 发布llvm和g…...

Using Multiple RDF Knowledge Graphs for Enriching ChatGPT Responses
本文是LLM系列文章,针对《Using Multiple RDF Knowledge Graphs for Enriching ChatGPT Responses》的翻译。 使用多个RDF知识图来丰富ChatGPT响应 摘要1 引言2 相关工作3 GPT-LODS的过程和用例4 结束语 摘要 最近有一种趋势是使用新型人工智能聊天GPT聊天箱&…...

【Hive-小文件合并】Hive外部分区表利用Insert overwrite的暴力方式进行小文件合并
这里我们直接用实例来讲解,Hive外部分区表有单分区多分区的不同情况,这里我们针对不同情况进行不同的方式处理。 利用overwrite合并单独日期的小文件 1、单分区 # 开启此表达式:(sample_date)?. set hive.support.quoted.identifiersnon…...

位运算 |(按位或) (按位与) ^(按位异或)
目录 文章目录:本章讲解的主要是刷题系列 1:首先会介绍 I & ^这三个操作符的作用,性质 2:三道使用位运算操作符的经典 笔试题(来自剑指offer) 题目链接如下: 1:136. 只出现一次的数字 - 力扣(LeetCode…...
Qt应用开发(基础篇)——复选按钮 QCheckBox 单选按钮 QRadioButton
一、前言 QCheckBox类与QRadioButton类继承于QAbstractButton,QCheckBox是一个带有文本标签的复选框,QRadioButton是一个带有文本标签的单选按钮。 按钮基类 QAbstractButton QCheckBox QCheckBox复选框是一个很常用的控件,拥有开关(选中和未…...

AERMOD模型大气环境影响评价
随着我国经济快速发展,我国面临着日益严重的大气污染问题。近年来,严重的大气污染问题已经明显影响国计民生,引起政府、学界和人们越来越多的关注。大气污染是工农业生产、生活、交通、城市化等方面人为活动的综合结果,同时气象因…...

递归组装树结构的数据
开发中,经常遇到存在树形结构的数据,如行政区划这类数据,一级一级分层,后端需要组装好树形结构数据返回给前端。 由于返给前端的json数据中,如果是叶子节点了,说明它没有子节点,那么就没必要返…...
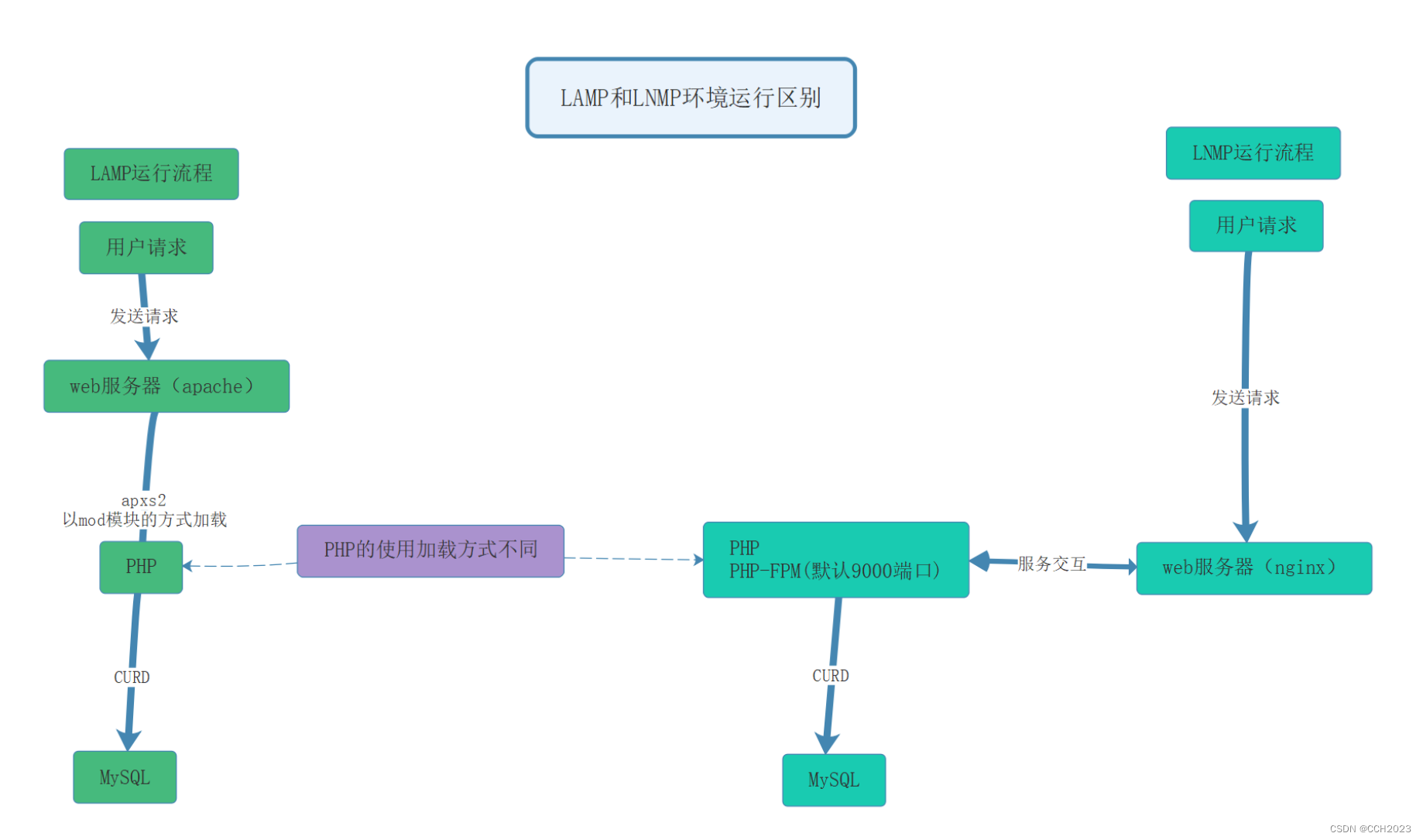
企业架构LNMP学习笔记7
PHP介绍: HTML:超文本标记语言 http: 超文本传输协议 端口80 浏览器将html代码解析成web页面。 PHP:超文本预处理器。后端语言开发,页面上需要动态改变修改的,需要连接数据库查询数据,转为html。 主要…...

开店星小程序上架教程和后台Request failed with status code 500[undefined]问题处理
开店星小程序上架教程和后台Request failed with status code 500[undefined]问题处理 刚刚安装好开店星网站后台之后都会出现这个code 500[undefined]的错误,需要改一下代码。改好了之后就可以正常使用了。如果大家不懂得这样处理的可以私聊我,帮忙处理…...

第一百三十六回 WillPopScope组件
文章目录 概念介绍使用方法示例代码 我们在上一章回中介绍了下拉刷新组件相关的内容,本章回中将介绍 WillPopScope组件.闲话休提,让我们一起Talk Flutter吧。 概念介绍 我们在本章回中介绍的WillPopScope组件是一种事件拦截类组件,它没有具…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
