【自执行闭包JS逆向】某网站登录MD5加密分析
文章目录
- 一、写在前面
- 二、抓包分析
- 三、加密函数分析
一、写在前面
最近工作比较忙,不过还是在督促自己利用有限的时间学习更新一些技术文章。互联网这个行业大家目前也都知道是非常内卷的,所有大家在工作之余养成良好的自主学习习惯是非常好的,多的就不说了,开始本期重点!
分析站点:
aHR0cHM6Ly9pLmZrdy5jb20v
在开始之前这里说一下“自执行”和“闭包”。它们概念相似,但不完全相同。自执行函数是一种函数,它在定义之后会立即执行,通常使用 (function() { /* code */ })(); 这种形式。闭包是一个更广泛的概念,它指的是一个函数能够访问并保存在其外部定义的变量的能力
二、抓包分析
这次分析的还是登陆参数,加密的对象是密码pwd。大家一定记得看看我之前写的这篇文章:JS逆向中快速搜索定位加密函数技巧总结
这里我们简单构造一个用户名密码进行登录抓包分析,密码就123456(MD5加密的话16位以49开头、32位e10或E10开头)

老规矩这里我们可以搜索pwd或者我们已经猜到加密方式,根据我上面文章的各个密码特征关键词搜索都是可以的:

像我上面所示,根据MD5加密算法的关键词1732584193进行搜索也能够快速定位到加密函数位置!
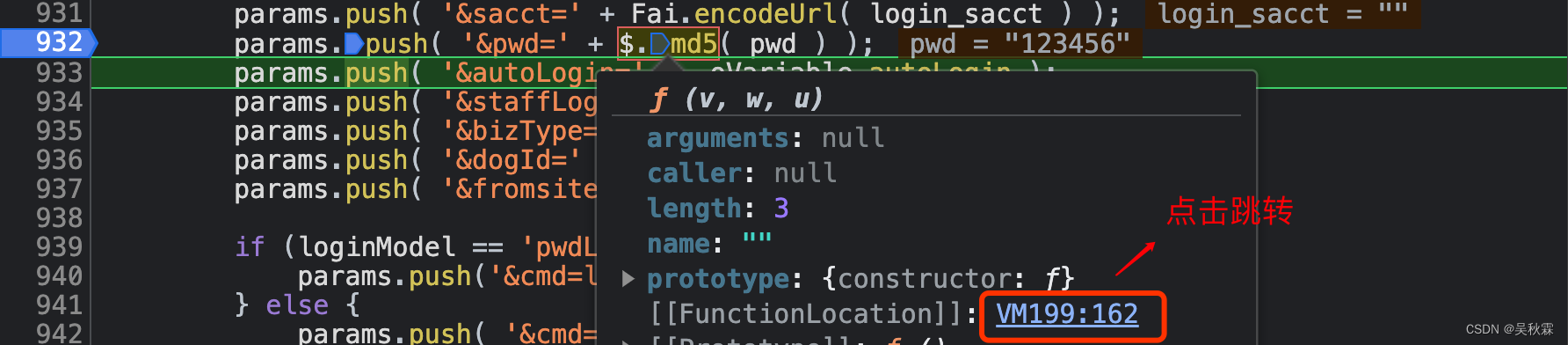
同样也可以搜索pwd或者断点方式调式找到加密加密位置,发现md5鼠标点击跳转到加密函数
三、加密函数分析
通过下图我们可以看到md5加密函数是一个自执行闭包函数,这里我们将*jQuery这部分稍微修改一下,无需引入 jQuery,修改加密JS代码如下:
(function(g) {function o(u, z) {var w = (u & 65535) + (z & 65535), v = (u >> 16) + (z >> 16) + (w >> 16);return (v << 16) | (w & 65535)}function s(u, v) {return (u << v) | (u >>> (32 - v))}function c(A, w, v, u, z, y) {return o(s(o(o(w, A), o(u, y)), z), v)}function b(w, v, B, A, u, z, y) {return c((v & B) | ((~v) & A), w, v, u, z, y)}function i(w, v, B, A, u, z, y) {return c((v & A) | (B & (~A)), w, v, u, z, y)}function n(w, v, B, A, u, z, y) {return c(v ^ B ^ A, w, v, u, z, y)}function a(w, v, B, A, u, z, y) {return c(B ^ (v | (~A)), w, v, u, z, y)}function d(F, A) {F[A >> 5] |= 128 << ((A) % 32);F[(((A + 64) >>> 9) << 4) + 14] = A;var w, z, y, v, u, E = 1732584193, D = -271733879, C = -1732584194, B = 271733878;for (w = 0; w < F.length; w += 16) {z = E;y = D;v = C;u = B;E = b(E, D, C, B, F[w], 7, -680876936);B = b(B, E, D, C, F[w + 1], 12, -389564586);C = b(C, B, E, D, F[w + 2], 17, 606105819);D = b(D, C, B, E, F[w + 3], 22, -1044525330);E = b(E, D, C, B, F[w + 4], 7, -176418897);B = b(B, E, D, C, F[w + 5], 12, 1200080426);C = b(C, B, E, D, F[w + 6], 17, -1473231341);D = b(D, C, B, E, F[w + 7], 22, -45705983);E = b(E, D, C, B, F[w + 8], 7, 1770035416);B = b(B, E, D, C, F[w + 9], 12, -1958414417);C = b(C, B, E, D, F[w + 10], 17, -42063);D = b(D, C, B, E, F[w + 11], 22, -1990404162);E = b(E, D, C, B, F[w + 12], 7, 1804603682);B = b(B, E, D, C, F[w + 13], 12, -40341101);C = b(C, B, E, D, F[w + 14], 17, -1502002290);D = b(D, C, B, E, F[w + 15], 22, 1236535329);E = i(E, D, C, B, F[w + 1], 5, -165796510);B = i(B, E, D, C, F[w + 6], 9, -1069501632);C = i(C, B, E, D, F[w + 11], 14, 643717713);D = i(D, C, B, E, F[w], 20, -373897302);E = i(E, D, C, B, F[w + 5], 5, -701558691);B = i(B, E, D, C, F[w + 10], 9, 38016083);C = i(C, B, E, D, F[w + 15], 14, -660478335);D = i(D, C, B, E, F[w + 4], 20, -405537848);E = i(E, D, C, B, F[w + 9], 5, 568446438);B = i(B, E, D, C, F[w + 14], 9, -1019803690);C = i(C, B, E, D, F[w + 3], 14, -187363961);D = i(D, C, B, E, F[w + 8], 20, 1163531501);E = i(E, D, C, B, F[w + 13], 5, -1444681467);B = i(B, E, D, C, F[w + 2], 9, -51403784);C = i(C, B, E, D, F[w + 7], 14, 1735328473);D = i(D, C, B, E, F[w + 12], 20, -1926607734);E = n(E, D, C, B, F[w + 5], 4, -378558);B = n(B, E, D, C, F[w + 8], 11, -2022574463);C = n(C, B, E, D, F[w + 11], 16, 1839030562);D = n(D, C, B, E, F[w + 14], 23, -35309556);E = n(E, D, C, B, F[w + 1], 4, -1530992060);B = n(B, E, D, C, F[w + 4], 11, 1272893353);C = n(C, B, E, D, F[w + 7], 16, -155497632);D = n(D, C, B, E, F[w + 10], 23, -1094730640);E = n(E, D, C, B, F[w + 13], 4, 681279174);B = n(B, E, D, C, F[w], 11, -358537222);C = n(C, B, E, D, F[w + 3], 16, -722521979);D = n(D, C, B, E, F[w + 6], 23, 76029189);E = n(E, D, C, B, F[w + 9], 4, -640364487);B = n(B, E, D, C, F[w + 12], 11, -421815835);C = n(C, B, E, D, F[w + 15], 16, 530742520);D = n(D, C, B, E, F[w + 2], 23, -995338651);E = a(E, D, C, B, F[w], 6, -198630844);B = a(B, E, D, C, F[w + 7], 10, 1126891415);C = a(C, B, E, D, F[w + 14], 15, -1416354905);D = a(D, C, B, E, F[w + 5], 21, -57434055);E = a(E, D, C, B, F[w + 12], 6, 1700485571);B = a(B, E, D, C, F[w + 3], 10, -1894986606);C = a(C, B, E, D, F[w + 10], 15, -1051523);D = a(D, C, B, E, F[w + 1], 21, -2054922799);E = a(E, D, C, B, F[w + 8], 6, 1873313359);B = a(B, E, D, C, F[w + 15], 10, -30611744);C = a(C, B, E, D, F[w + 6], 15, -1560198380);D = a(D, C, B, E, F[w + 13], 21, 1309151649);E = a(E, D, C, B, F[w + 4], 6, -145523070);B = a(B, E, D, C, F[w + 11], 10, -1120210379);C = a(C, B, E, D, F[w + 2], 15, 718787259);D = a(D, C, B, E, F[w + 9], 21, -343485551);E = o(E, z);D = o(D, y);C = o(C, v);B = o(B, u)}return [E, D, C, B]}function p(v) {var w, u = "";for (w = 0; w < v.length * 32; w += 8) {u += String.fromCharCode((v[w >> 5] >>> (w % 32)) & 255)}return u}function j(v) {var w, u = [];u[(v.length >> 2) - 1] = undefined;for (w = 0; w < u.length; w += 1) {u[w] = 0}for (w = 0; w < v.length * 8; w += 8) {u[w >> 5] |= (v.charCodeAt(w / 8) & 255) << (w % 32)}return u}function k(u) {return p(d(j(u), u.length * 8))}function f(w, z) {var v, y = j(w), u = [], x = [], A;u[15] = x[15] = undefined;if (y.length > 16) {y = d(y, w.length * 8)}for (v = 0; v < 16; v += 1) {u[v] = y[v] ^ 909522486;x[v] = y[v] ^ 1549556828}A = d(u.concat(j(z)), 512 + z.length * 8);return p(d(x.concat(A), 512 + 128))}function t(w) {var z = "0123456789abcdef", v = "", u, y;for (y = 0; y < w.length; y += 1) {u = w.charCodeAt(y);v += z.charAt((u >>> 4) & 15) + z.charAt(u & 15)}return v}function m(u) {return unescape(encodeURIComponent(u))}function q(u) {return k(m(u))}function l(u) {return t(q(u))}function h(u, v) {return f(m(u), m(v))}function r(u, v) {return t(h(u, v))}g.md5 = function(v, w, u) {if (!w) {if (!u) {return l(v);} else {return q(v);}}if (!u) {return r(w, v);} else {return h(w, v);}}
}(typeof window !== "undefined" ? window : this));
最后我们使用JS调试工具就能验证了,这里我直接在控制台把扣出来的JS加密函数贴进去调用测试如下:
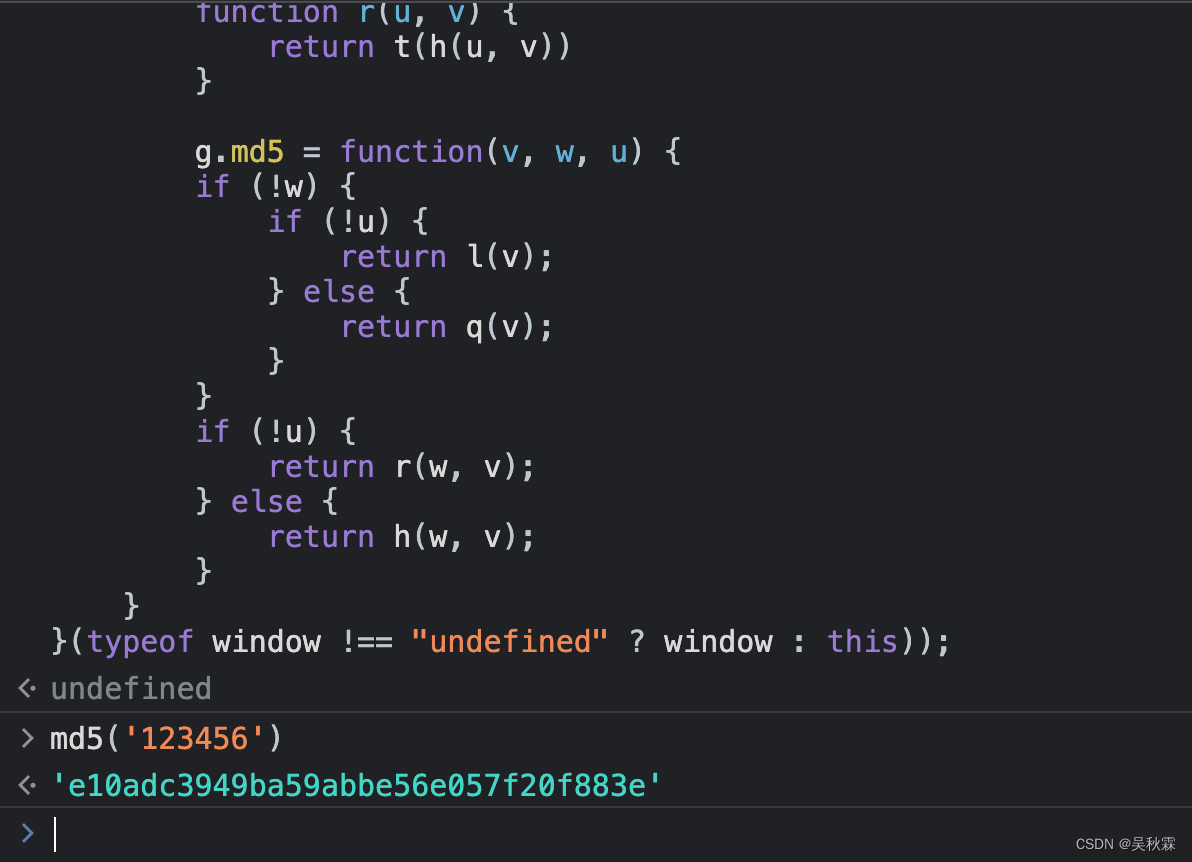
好了,到这里又到了跟大家说再见的时候了。创作不易,帮忙点个赞再走吧。你的支持是我创作的动力,希望能带给大家更多优质的文章
相关文章:

【自执行闭包JS逆向】某网站登录MD5加密分析
文章目录 一、写在前面二、抓包分析三、加密函数分析 一、写在前面 最近工作比较忙,不过还是在督促自己利用有限的时间学习更新一些技术文章。互联网这个行业大家目前也都知道是非常内卷的,所有大家在工作之余养成良好的自主学习习惯是非常好的ÿ…...
Stable Diffuse 之 安装文件夹、以及操作界面 UI 、Prompt相关说明
Stable Diffuse 之 安装文件夹、以及操作界面 UI 、Prompt相关说明 目录 Stable Diffuse 之 安装文件夹、以及操作界面 UI 、Prompt相关说明 一、简单介绍 二、安装文件相关说明 三、界面的简单说明 四、prompt 的一些语法简单说明 1、Prompt :正向提示词 &am…...

【Linux】- 一文秒懂shell编程
shell编程 1.1 Shell 是什么1.2 Shell 脚本的执行方式1.3 编写第一个 Shell 脚本2.1 Shell 的变量2.2 shell 变量的定义2.3 设置环境变量3.1 位置参数变量3.2 预定义变量4.1 运算符4.2 条件判断5.1 流程控制5.2 case 语句5.3 for 循环5.4 while 循环5.5 read基本语法6.1函数6.2…...

CentOS下多网卡绑定多IP段时导致只有一个会通的问题解决
CentOS下多网卡绑定多IP段时导致只有一个会通的问题解决 虚拟机配置多个网络地址,结果同时只能有一个ip是通的, 原因:Linux默认开启了反向路由检查导致的,比如说外面访问eth0的网卡,而网关在eth1上,又或者从…...

关于实现 Vue 动态数据显示,比如数字 0 或 1 怎么显示为 男 或 女等等的动态显示实现方法
具体 Vue 代码演示: test.vue 文件演示: <template> <!-- 方法一 --> <div>{{ test.data 0 ? 男 : 女}}</div><!-- 方法二 --> <div>{{ test.data 0 ? 男 : }}{{ test.data 1 ? 女 : }}{{ test.d…...
mac制作ssl证书|生成自签名证书,nodejs+express在mac上搭建https+wss(websocket)服务器
注意 mac 自带 openssl 所以没必要像 windows 一样先安装 openssl,直接生成即可 生成 ssl/自签名 证书 生成 key # 生成rsa私钥,des3算法,server_ssl.key是秘钥文件名 1024位强度 openssl genrsa -des3 -out server_ssl.key 1024让输入两…...

Unix System V BSD POSIX 究竟是什么?
学习Linux系统,很多同学对这些单词概念很模糊、一脸懵逼! 黄老师觉得,了解了历史,才会真正明白这些单词的含义,坐稳、黄老师发车了!!! 首先介绍一下什么是Unix? UNIX(非复用信息和计算机服务,英语:Uniplexed Information and Computing Service,UnICS)取“UNI…...
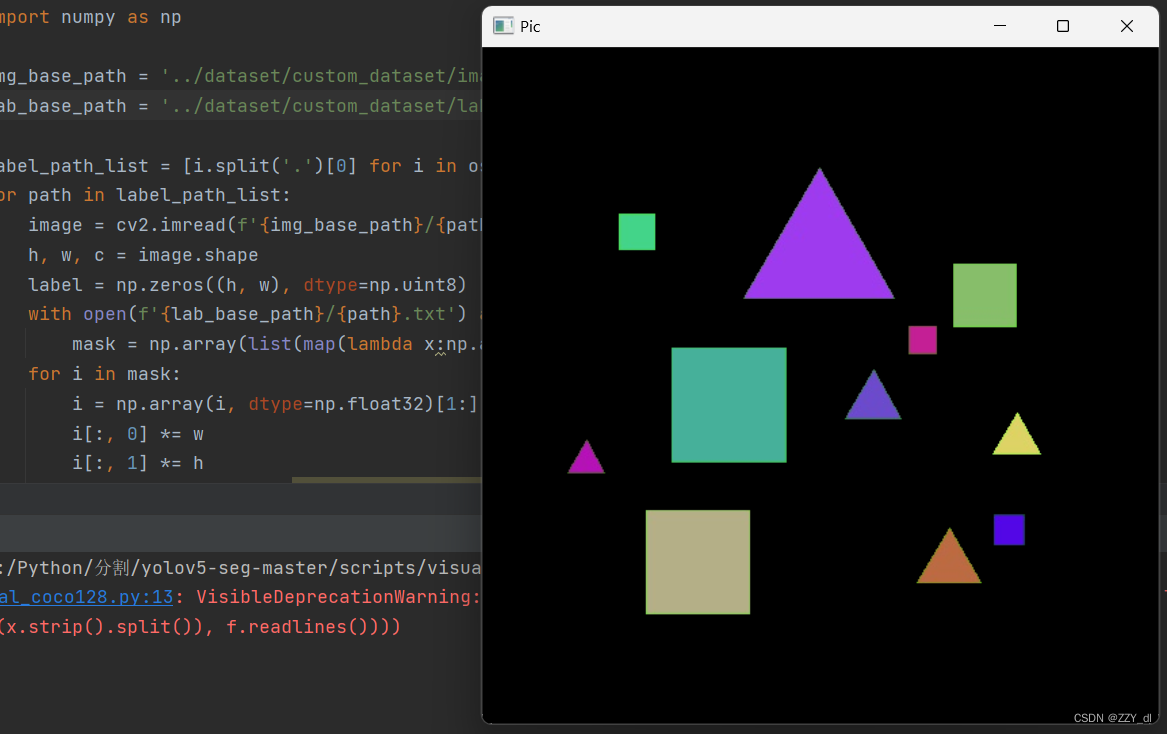
数据集学习笔记(六):目标检测和图像分割标注软件介绍和使用,并转换成YOLO系列可使用的数据集格式
文章目录 一、目标检测1.1 labelImg1.2 介绍1.3 安装1.4 使用1.5 转换1.6 验证 二、图像分割2.1 labelme2.2 介绍2.3 安装2.4 使用2.5 转换2.6 验证 一、目标检测 1.1 labelImg 1.2 介绍 labelImg是一个开源的图像标注工具,用于创建图像标注数据集。它提供了一个…...
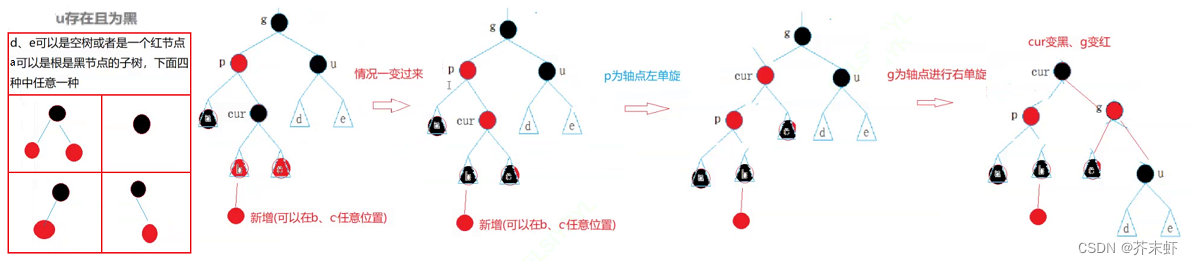
【高阶数据结构】红黑树 {概念及性质;红黑树的结构;红黑树的实现;红黑树插入操作详细解释;红黑树的验证}
红黑树 一、红黑树的概念 红黑树(Red Black Tree) 是一种自平衡二叉查找树,在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有…...

获取对象占用内存
添加依赖 <dependency><groupId>org.apache.lucene</groupId><artifactId>lucene-core</artifactId><version>4.0.0</version> </dependency>添加vm启动参数 --add-opens java.base/java.langALL-UNNAMED --add-opens java.ba…...
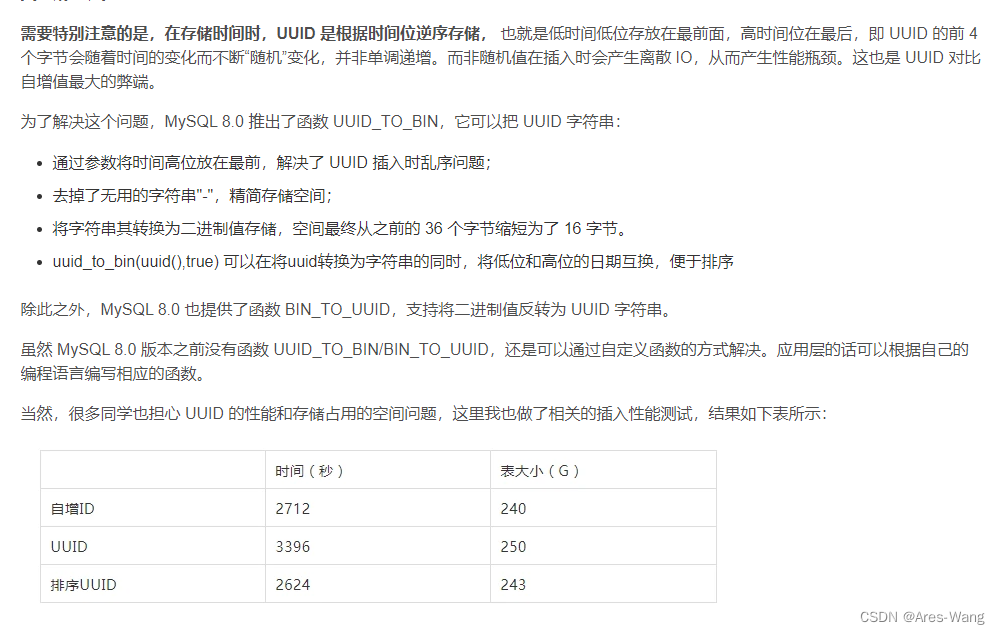
mysql UUID 作为主键的问题
UUID 在MySQL中,可以使用UUID()函数来生成一个新的UUID值。该函数的返回值是一个字符串类型,表示一个32位的十六进制数字,其中包含4个连字符“-”,例如:“6ccd780c-baba-1026-9564-0040f4311e29”。 varchar(32) 32*4…...

2023高教社杯全国大学生数学建模竞赛选题建议
如下为C君的2023高教社杯全国大学生数学建模竞赛(国赛)选题建议, 提示:DS C君认为的难度:C<B<A,开放度:B<A<C 。 D、E题推荐选E题,后续会直接更新E论文和思路…...

分类预测 | MATLAB实现GRNN广义回归神经网络多特征分类预测
分类预测 | MATLAB实现GRNN广义回归神经网络多特征分类预测 目录 分类预测 | MATLAB实现GRNN广义回归神经网络多特征分类预测分类效果基本介绍模型描述预测过程程序设计参考资料分类效果 基本介绍 MATLAB实现GRNN广义回归神经网络多特...

低功耗窗帘电机解决方案成功应用并通过 Matter 1.1 认证
Nordic Semiconductor官方宣布与HooRii Tech(和众科技)携手合作,基于 Nordic nRF52840 芯片平台打造的 HRN71模组,成功赋能低功耗窗帘电机品牌发布Matter产品。低功耗窗帘电机获得 Matter 1.1 认证意味着它具有与其他 Matter 认证…...

如何修复老照片?老照片修复翻新的方法
老旧照片,尤其是黑白照片,往往因为年代久远、保存方式不当等原因而出现褪色、污损、划痕等问题,会比较难以修复,就算是技术精湛的专业修复师,也是需要投入极大时间精力的,效果也是不可预料的。 修复老照片…...
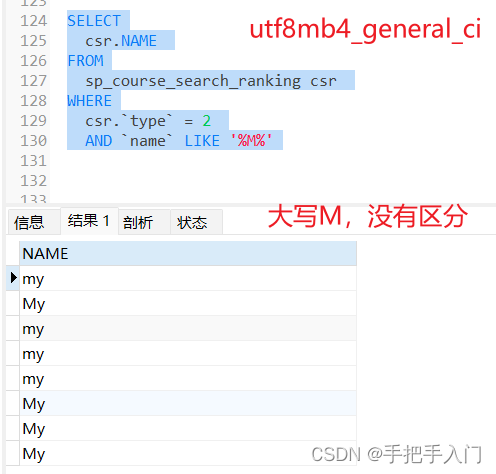
MySQL:区分大小写
查看MySQL版本 show variables; 1、查看 MySQL 当前的区分大小写设置: SHOW VARIABLES LIKE lower_case_table_names; 或者 show Variables like %table_names 2、更改大小写敏感设置: 在 MySQL 5.7 中,更改大小写敏感设置要求修改配置文件 …...

刷题笔记19——优势洗牌和去重保持字典序
摆出无比亲密的态度,装模作样地与对方套近乎,频繁地联系对方。这都说明他们并不相信自己得到了对方的信赖,若是互相信赖,便不会依赖亲密的感觉。在外人看来,反而显得冷淡。 ——尼采《人性的,太人性的》 ha…...
星际争霸之小霸王之小蜜蜂(十一)--杀杀杀
系列文章目录 星际争霸之小霸王之小蜜蜂(十)--鼠道 星际争霸之小霸王之小蜜蜂(九)--狂鼠之灾 星际争霸之小霸王之小蜜蜂(八)--蓝皮鼠和大脸猫 星际争霸之小霸王之小蜜蜂(七)--消失…...

腾讯云免费SSL证书申请流程_每年免费50个HTTPS证书
2023腾讯云免费SSL证书申请流程,一个腾讯云账号可以申请50张免费SSL证书,免费SSL证书为DV证书,仅支持单一域名,申请腾讯云免费SSL证书3分钟即可申请成功,免费SSL证书品牌为TrustAsia亚洲诚信,腾讯云百科分享…...

C#上位机开发目录
C#上位机序列1: 多线程(线程同步,事件触发,信号量,互斥锁,共享内存,消息队列) C#上位机序列2: 同步异步(async、await) C#上位机序列3: 流程控制(串行,并行,…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
