不就是G2O嘛
从零开始一起学习SLAM | 理解图优化,一步步带你看懂g2o代码
SLAM的后端一般分为两种处理方法,一种是以扩展卡尔曼滤波(EKF)为代表的滤波方法,一种是以图优化为代表的非线性优化方法。不过,目前SLAM研究的主流热点几乎都是基于图优化的。
顺便总结下滤波方法的优缺点:
优点:在当时计算资源受限、待估计量比较简单的情况下,EKF为代表的滤波方法比较有效,经常用在激光SLAM中。
缺点:它的一个大缺点就是存储量和状态量是平方增长关系,因为存储的是协方差矩阵,因此不适合大型场景。而现在基于视觉的SLAM方案,路标点(特征点)数据很大,滤波方法根本吃不消,所以此时滤波的方法效率非常低。
在SLAM里,图优化一般分解为两个任务:
1、构建图。机器人位姿作为顶点,位姿间关系作为边。
2、优化图。调整机器人的位姿(顶点)来尽量满足边的约束,使得误差最小。
g2o安装很简单,参考GitHub上官网:
https://github.com/RainerKuemmerle/g2o

1.顶点和边
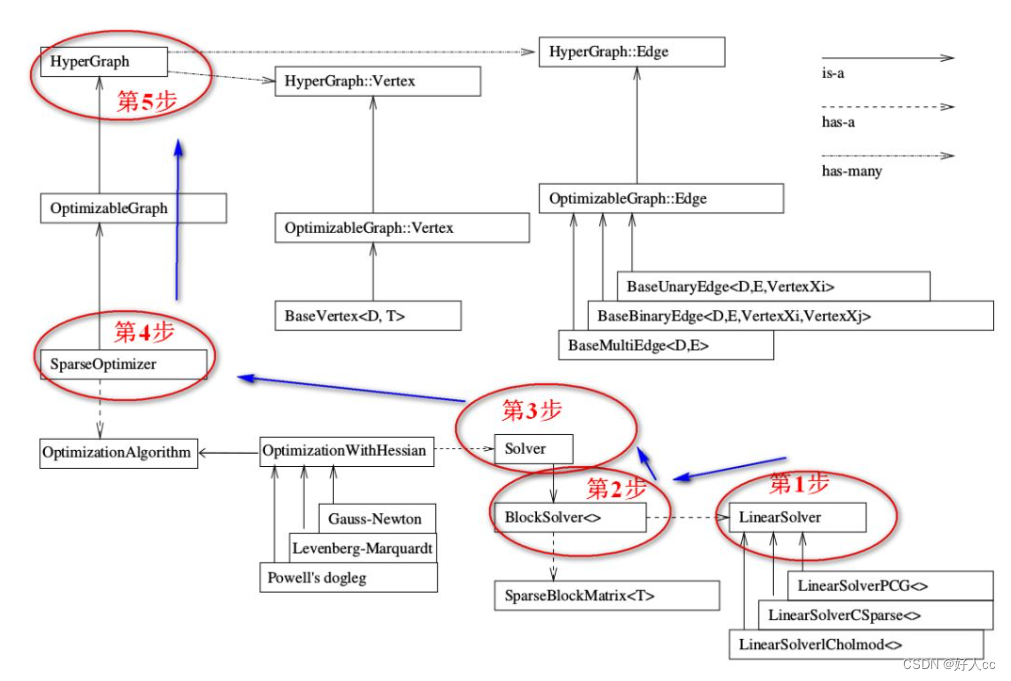
注意看 has-many 箭头,你看这个超图包含了许多顶点(HyperGraph::Vertex)和边(HyperGraph::Edge)。而这些顶点顶点继承自 Base Vertex,也就是OptimizableGraph::Vertex,而边可以继承自 BaseUnaryEdge(单边), BaseBinaryEdge(双边)或BaseMultiEdge(多边),它们都叫做OptimizableGraph::Edge
2.配置SparseOptimizer的优化算法和求解器
整个图的核心SparseOptimizer 包含一个优化算法(OptimizationAlgorithm)的对象。OptimizationAlgorithm是通过OptimizationWithHessian 来实现的。其中迭代策略可以从Gauss-Newton(高斯牛顿法,简称GN), Levernberg-Marquardt(简称LM法), Powell's dogleg 三者中间选择一个(我们常用的是GN和LM)
3.如何求解
OptimizationWithHessian 内部包含一个求解器(Solver),这个Solver实际是由一个BlockSolver组成的。这个BlockSolver有两个部分,一个是SparseBlockMatrix ,用于计算稀疏的雅可比和Hessian矩阵;一个是线性方程的求解器(LinearSolver),它用于计算迭代过程中最关键的一步HΔx=−b,LinearSolver有几种方法可以选择:PCG, CSparse, Choldmod,具体定义后面会介绍
高博在十四讲中g2o求解曲线参数的例子来说明,源代码地址
https://github.com/gaoxiang12/slambook/edit/master/ch6/g2o_curve_fitting/main.cpp
typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block; // 每个误差项优化变量维度为3,误差值维度为1// 第1步:创建一个线性求解器LinearSolver
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 第2步:创建BlockSolver。并用上面定义的线性求解器初始化
Block* solver_ptr = new Block( linearSolver ); // 第3步:创建总求解器solver。并从GN, LM, DogLeg 中选一个,再用上述块求解器BlockSolver初始化
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );// 第4步:创建终极大boss 稀疏优化器(SparseOptimizer)
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm( solver ); // 设置求解器
optimizer.setVerbose( true ); // 打开调试输出// 第5步:定义图的顶点和边。并添加到SparseOptimizer中
CurveFittingVertex* v = new CurveFittingVertex(); //往图中增加顶点
v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addVertex( v );
for ( int i=0; i<N; i++ ) // 往图中增加边
{CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );edge->setId(i);edge->setVertex( 0, v ); // 设置连接的顶点edge->setMeasurement( y_data[i] ); // 观测数值edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆optimizer.addEdge( edge );//设置迭代次数
}// 第6步:设置优化参数,开始执行优化
optimizer.initializeOptimization();
optimizer.optimize(100);1.线性求解器
LinearSolverCholmod :使用sparse cholesky分解法。继承自LinearSolverCCS
LinearSolverCSparse:使用CSparse法。继承自LinearSolverCCS
LinearSolverPCG :使用preconditioned conjugate gradient 法,继承自LinearSolver
LinearSolverDense :使用dense cholesky分解法。继承自LinearSolver
LinearSolverEigen: 依赖项只有eigen,使用eigen中sparse Cholesky 求解,因此编译好后可以方便的在其他地方使用,性能和CSparse差不多。继承自LinearSolver2.创建BlockSolver。并用上面定义的线性求解器初始化。
BlockSolver 内部包含 LinearSolver,用上面我们定义的线性求解器LinearSolver来初始化。
你点进去会发现 BlockSolver有两种定义方式,一种是指定的固定变量的solver,我们来看一下定义
using BlockSolverPL = BlockSolver< BlockSolverTraits<p, l> >;其中p代表pose的维度(注意一定是流形manifold下的最小表示),l表示landmark的维度
另一种是可变尺寸的solver,定义如下
using BlockSolverX = BlockSolverPL<Eigen::Dynamic, Eigen::Dynamic>;这是因为在某些应用场景,我们的Pose和Landmark在程序开始时并不能确定,那么此时这个块状求解器就没办法固定变量,此时使用这个可变尺寸的solver,所有的参数都在中间过程中被确定另外你看block_solver.h的最后,预定义了比较常用的几种类型,如下所示:
BlockSolver_6_3 :表示pose 是6维,观测点是3维。用于3D SLAM中的BA
BlockSolver_7_3:在BlockSolver_6_3 的基础上多了一个scale
BlockSolver_3_2:表示pose 是3维,观测点是2维3.创建总求解器solver。并从GN, LM, DogLeg 中选一个,再用上述块求解器BlockSolver初始化
你点进去 GN、 LM、 Doglet算法内部,会发现他们都继承自同一个类OptimizationWithHessian,如下图所示,这也和我们最前面那个图是相符的。然后,我们点进去看 OptimizationAlgorithmWithHessian,发现它又继承自OptimizationAlgorithm,这也和前面的相符,总之,在该阶段,我们可以选则三种方法:
g2o::OptimizationAlgorithmGaussNewton
g2o::OptimizationAlgorithmLevenberg
g2o::OptimizationAlgorithmDogleg 4.创建终极大boss 稀疏优化器(SparseOptimizer),并用已定义求解器作为求解方法。
创建稀疏优化器
g2o::SparseOptimizer optimizer;用前面定义好的求解器作为求解方法:
SparseOptimizer::setAlgorithm(OptimizationAlgorithm* algorithm)其中setVerbose是设置优化过程输出信息用的
SparseOptimizer::setVerbose(bool verbose)5.定义图的顶点和边。并添加到SparseOptimizer中。
6.设置优化参数,开始执行优化。
设置SparseOptimizer的初始化、迭代次数、保存结果等。
SparseOptimizer::initializeOptimization(HyperGraph::EdgeSet& eset)设置迭代次数,然后就开始执行图优化了。
SparseOptimizer::optimize(int iterations, bool online)https://www.jianshu.com/p/e16ffb5b265d
https://blog.csdn.net/heyijia0327/article/details/47686523
相关文章:

不就是G2O嘛
从零开始一起学习SLAM | 理解图优化,一步步带你看懂g2o代码 SLAM的后端一般分为两种处理方法,一种是以扩展卡尔曼滤波(EKF)为代表的滤波方法,一种是以图优化为代表的非线性优化方法。不过,目前SLAM研究的主…...
C#开发的OpenRA游戏之系统参数选项按钮
C#开发的OpenRA游戏之系统参数选项按钮 前面分析了信标按钮,从图上可以看到,靠右边的按钮,就是系统参数选项按钮: 这个按钮与前面三个按钮是不一样的,虽然它们在排列位置上是放在一起,但是处理的方法方式是不一样的,因为这个选项按钮,并不需要发命令给服务器,再返回来…...

苹果启动2024年SRDP计划:邀请安全专家使用定制iPhone寻找漏洞
苹果公司昨天(8月30日)正式宣布开始接受2024 年iPhone安全研究设备计划的申请,iOS 安全研究人员可以在 10 月底之前申请安全研究设备 SRD。 SRD设备是专门向安全研究人员提供的iPhone14Pro,该设备具有专为安全研究而设计的特殊硬…...
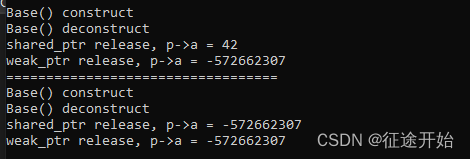
std::make_shared和new初始化智能指针的区别
先看代码: class Base {public:Base(int num):a(num) {std::cout << "Base() construct" << std::endl;}~Base() {std::cout << "Base() deconstruct" << std::endl;}int Get() {return a;}private:int a; };void tes…...

无涯教程-JavaScript - ERFC.PRECISE函数
描述 ERFC.PRECISE函数返回x和无穷大之间集成的互补ERF函数。 互补误差函数等于1-ERF(即1-误差函数),由等式给出- $$Erfc(x) \frac {2} {\sqrt {\pi}} \int_ {x} ^ {\infty} e ^ {-t ^ 2} dt $$ 语法 ERFC.PRECISE(x)争论 Argument描述Required/OptionalxThe lower bound…...

2023国赛数学建模C题思路分析 - 蔬菜类商品的自动定价与补货决策
# 1 赛题 在生鲜商超中,一般蔬菜类商品的保鲜期都比较短,且品相随销售时间的增加而变差, 大部分品种如当日未售出,隔日就无法再售。因此, 商超通常会根据各商品的历史销售和需 求情况每天进行补货。 由于商超销售的蔬菜…...

手写Spring:第1章-开篇介绍,手写Spring
文章目录 一、手写Spring二、Spring 生命周期 一、手写Spring 💡 目标:我们该对 Spring 学到什么程度?又该怎么学习呢? 手写简化版 Spring 框架,了解 Spring 核心原理,为后续再深入学习 Spring 打下基础。在…...

C语言中,字节对齐是一种重要的内存管理概念
C语言中,字节对齐是一种重要的内存管理概念 字节对齐的目的是为了提高内存访问的效率。因为CPU访问内存的最小单位是字节,所以如果数据结构的成员以正确的字节边界对齐,那么CPU就可以直接访问这些成员,而不需要进行额外的内存移动…...
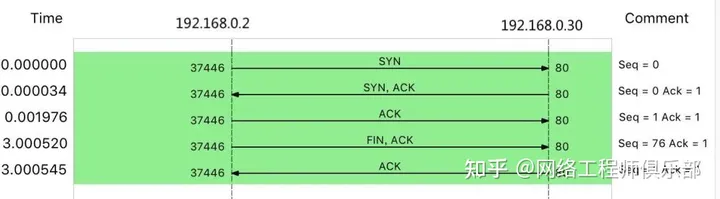
网络丢包问题,敢不敢这样定位?
下午好,我的网工朋友。 所谓丢包,是指在网络数据的收发过程中,由于种种原因,数据包还没传输到应用程序中,就被丢弃了。 这些被丢弃包的数量,除以总的传输包数,也就是我们常说的丢包率。 丢包…...
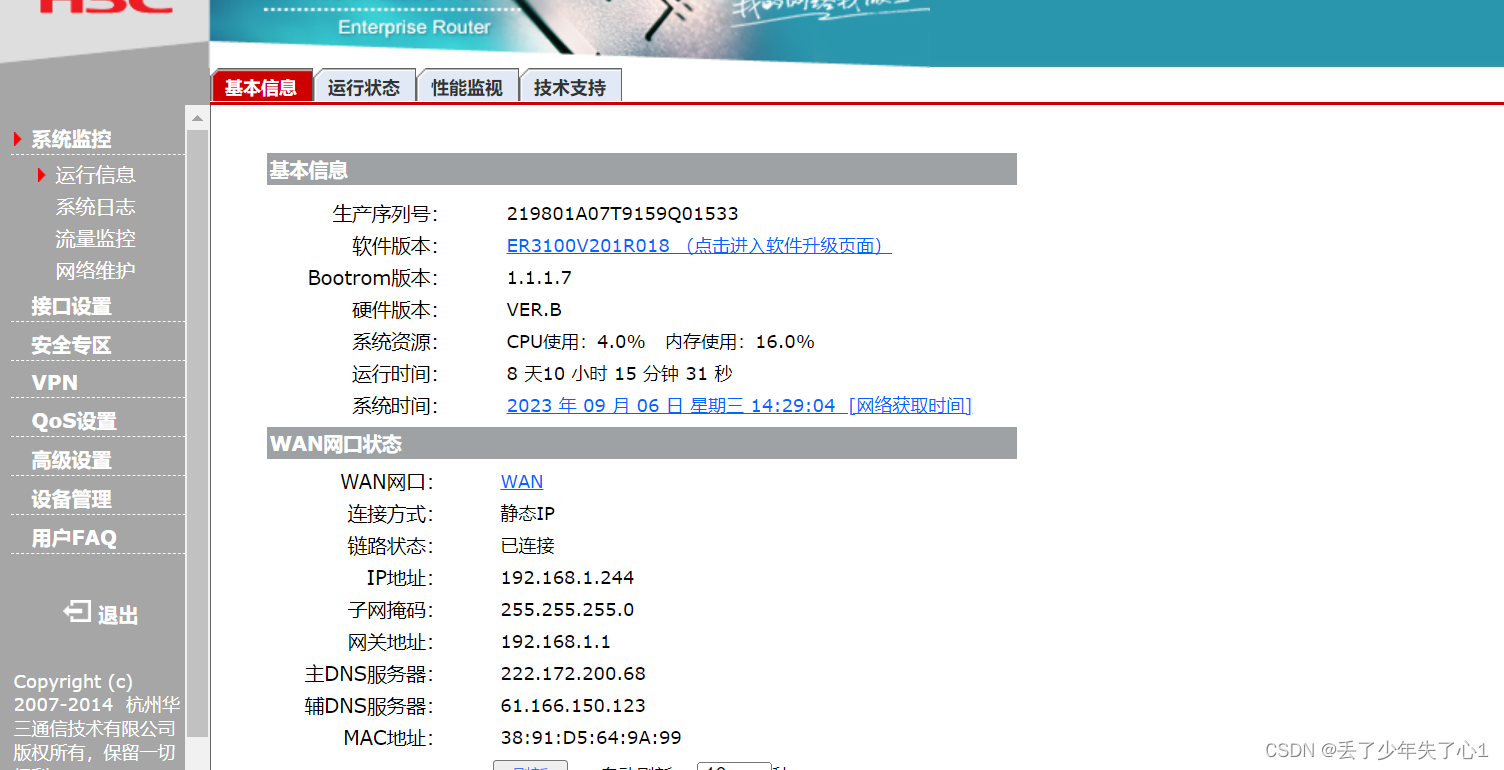
【漏洞复现】H3C路由器信息泄露任意用户登录
漏洞描述 通过访问特地址得到密码可进行登录。 免责声明 技术文章仅供参考,任何个人和组织使用网络应当遵守宪法法律,遵守公共秩序,尊重社会公德,不得利用网络从事危害国家安全、荣誉和利益,未经授权请勿利用文章中…...

随机数算法,SQL
SELECT* FROMprizes_config WHEREweight > ( SELECT FLOOR( RAND() * MAX( weight )) FROM prizes_config ) order by weight asc-- LIMIT 1;记录 id 权重 1 5 2 10 3 50 4 100 找权重最大的那个值,调用rand()函数&#…...

什么是软件测试+软件测试的分类【软件测试】
软件测试 什么是软件? 软件 程序 数据 文档 软件测试的对象有哪些?程序 数据 文档 C/S与B/S架构 C/S:客户端服务器,这种就是我们一定要安装一个客户端才能够用的软件,就叫C/S。比如:微信、qq B/S&am…...

2023国赛C题解题思路:蔬菜类商品的自动定价与补货决策
本次将全程提供国赛C题完整解题思路及代码,同时共享一些国赛论文模板等资料,需要的小伙伴可以关注一下,持续更新!大家也可以关注B站视频:不知名数学家小P 实时更新 本次C题是一道较为简单的统计分析题目,建…...

MIT6.824 Spring2021 Lab 1: MapReduce
文章目录 0x00 准备0x01 MapReduce简介0x02 RPC0x03 调试0x04 代码coordinator.gorpc.goworker.go 0x00 准备 阅读MapReduce论文配置GO环境 因为之前没用过GO,所以 先在网上学了一下语法A Tour of Go 感觉Go的接口和方法的语法和C挺不一样, 并发编程也挺有意思 0x01 MapRed…...

JavaScript 日期 – 如何使用 DayJS 库在 JS 中处理日期和时间
当涉及到在 JavaScript 中处理日期和时间时,开发人员经常发现自己正在努力应对内置对象的复杂性Date。 虽然普通 JavaScript 提供了基本功能,但使用起来可能相当麻烦,尤其是在处理解析、格式化和操作日期时。 这就是像 DayJS 这样的外部库发挥作用的地方,它提供了大量的优…...

Docker基础入门:Docker基础总结篇--超详细
Docker基础入门:Docker基础总结篇[docker3要素、docker安装配置、容器使用、镜像管理发布] 一、Docker 3要素1.1、镜像(Image)1.2、容器(Container)1.3、仓库(Registry)1.4 、总结 二、Docker安…...
对象临时中间状态的条件竞争覆盖
Portswigger练兵场之条件竞争 🦄条件竞争之对象临时中间状态的条件竞争 Lab: Partial construction race conditions🚀实验前置必要知识点 某些框架尝试通过使用某种形式的请求锁定来防止意外的数据损坏。例如,PHP 的本机会话处理程序模块…...
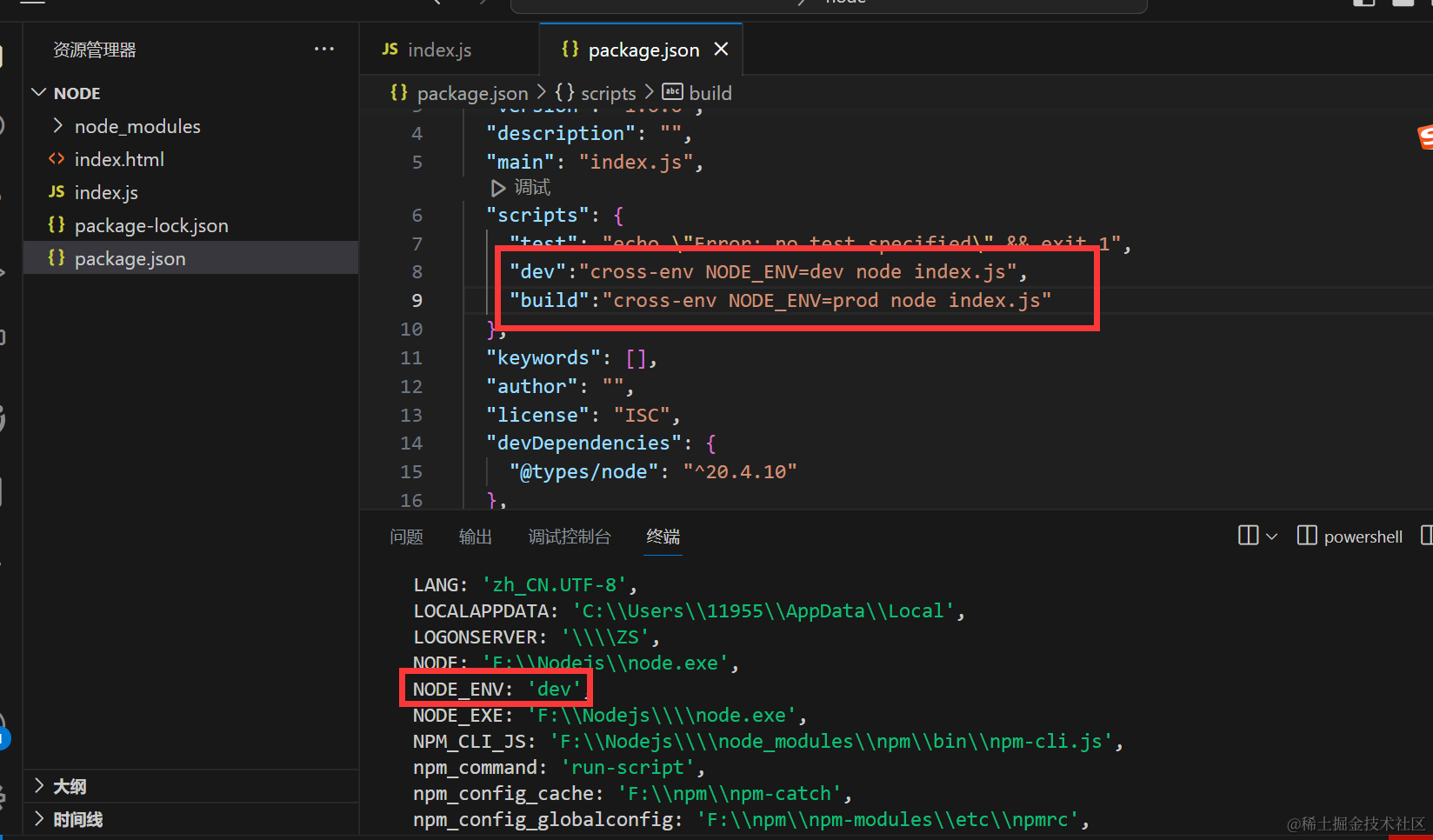
Nodejs 第十四章(process)
process 是Nodejs操作当前进程和控制当前进程的API,并且是挂载到globalThis下面的全局API API 介绍 1. process.arch 返回操作系统 CPU 架构 跟我们之前讲的os.arch 一样 arm、arm64、ia32、mips、mipsel、ppc、ppc64、s390、s390x、以及 x64 2. process.cwd() …...
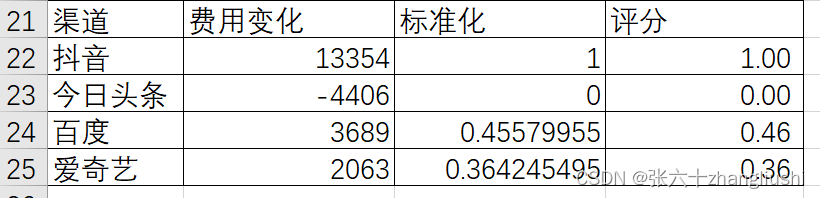
数据分析因子评分学习
当多个因素影响一个结果时,我们需要综合考虑这些因素分别对结果德影响。因子评分就是用于比较其对结果德影响程度。 文章目录 前言一、案例背景二、解决方案(一)分析思路(二)剔除无关数据(三)求…...

【postgresql 基础入门】数据库服务的管理
数据库服务管理 专栏内容: postgresql内核源码分析手写数据库toadb并发编程 开源贡献: toadb开源库 个人主页:我的主页 管理社区:开源数据库 座右铭:天行健,君子以自强不息;地势坤ÿ…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
