对时序数据进行分类与聚类
我在最近的工作中遇到了一个问题,问题是我需要根据银行账户在一定时间内的使用信息对该账户在未来的一段时间是否会被销户进行预测。这是一个双元值的分类问题,只有两种可能,即会被销户和不会被销户。针对这个问题一般来说有两种解决策略。
- 提取时间序列的统计学特征值,例如最大值,最小值,均值等。然后利目前常用的算法根据提取的特征进行分类,例如Naive Bayes, SVMs 等。
- k-NN方法。针对想要预测的时间序列,在训练集中找一个跟它最相似的另外一个序列,然后利用找到的序列的输出值作为原序列的预测值。
下面我会使用这两种算法,运行并对比结果,然后找到最合适的算法。
找到相似数据
针对这个问题,一般会使用欧氏距离寻找相似,但这种方法存在很多问题。如下文给出的示例。如图所示,有三个时间序列:

很明显,序列ts1和ts2的相似度更高,ts3和其他两个相比的差异性更大。为了验证结果,可以通过编程求得这三个序列之间的欧氏距离d(ts1, ts2)和d(ts1,ts3)。下面编写一个计算欧氏距离的函数:
def euclid_dist(t1,t2):return sqrt(sum((t1-t2)**2))
通过计算,结果是d(ts1,ts2)=26.9,d(ts1,ts3)=23.2。很明显,与我们直觉判断相悖。这就是利用欧氏距离标准来判定相似性存在的问题。为了解决这个问题,引入另一个方法——DTW。
动态时间规整(Dynamic Time Warping, DTW)
DTW可以针对两个时间序列找到最优的非线定位(non-linear alignment)。定位之间的欧氏距离不太容易受到时间轴方向上的失真所造成的负面相似性测量的影响。但是我们也必须为这种方法付出代价,即DTW是所有用到的时间序列的数据数量的二次方。
DTW的工作方式如下。我们可以引入两个时间序列Q和C,这两个时间序列都拥有n个数据点,Q=q_1, q_2, \cdots, q_n和C=c_1, c_2, \cdots, c_n。首先我们用这两个时间序列去构造一个n\times n的矩阵,这个矩阵中的第i,j^{th}项代表的是数据点q_i和c_j之间的欧氏距离。我们需要通过这个矩阵找到一个变量,通过该变量可以使所有的欧氏距离和最小。这个变量可以决定两个时间序列之间的最优非线性定位。需要注意的是,对于其中一个时间序列上的数据点,它是有可能映射到另一条时间序列上的多个数据点。
我们可以把这个变量记作W,W = w_1,w_2,\cdots,w_n。其中每一个W代表的都是Q中的第i个点与C中的第j个点之间的距离,即w_k=(q_i-c_j)^2。
因为我们需要找到这个变量的最小值,即W^*=argmin_W(\sqrt{\sum_{k=1}^{K}w_k}),为了找到这个值我们需要通过动态的方法,特别是接下来的这个递归函数。\gamma(i,j)=d(q_i,c_j)+min(\gamma(i-1,j-1),\gamma(i-1,j),\gamma(i,j-1))。该算法可以通过以下的Python代码实现。
def DTWDistance(s1, s2):DTW={}for i in range(len(s1)):DTW[(i, -1)] = float('inf')for i in range(len(s2)):DTW[(-1, i)] = float('inf')DTW[(-1, -1)] = 0for i in range(len(s1)):for j in range(len(s2)):dist= (s1[i]-s2[j])**2DTW[(i, j)] = dist + min(DTW[(i-1, j)],DTW[(i, j-1)], DTW[(i-1, j-1)])return sqrt(DTW[len(s1)-1, len(s2)-1])
通过DTW计算,DTWDistance(ts1,ts2)=17.9,DTWDDistance(ts1,ts3)=21.5。正如我们所看到的,该结果与只利用欧氏距离算法得到的结果截然不同。现在,这个结果就符合我们的主观腿断了,即ts2相比于ts3与ts1更为相似。
提高DTW算法计算速度
DTW的复杂度O(nm)是与两个时间序列的数据数量正相关的。如果两个时间序列都含有大量数据,那么这种方法的计算时间会非常长。因此我们需要通过一些方法去提高计算速度。第一种方法是强制执行局部性约束。这种方法假设当i和j相距太远,则q_i和c_j不需要匹配。这个阈值则由一个给定的窗口大小w决定。这种方法可以提高窗口内循环的速度。详细代码如下:
def DTWDistance(s1, s2, w):DTW={}w = max(w, abs(len(s1)-len(s2)))for i in range(-1,len(s1)): for j in range(-1,len(s2)):DTW[(i, j)] = float('inf')DTW[(-1, -1)] = 0for i in range(len(s1)):for j in range(max(0, i-w), min(len(s2), i+w)):dist= (s1[i]-s2[j])**2DTW[(i, j)] = dist + min(DTW[(i-1, j)],DTW[(i, j-1)], DTW[(i-1, j-1)])return sqrt(DTW[len(s1)-1, len(s2)-1])
另一种方法是使用LB Keogh下界方法DTW的边界。
LBKeogh(Q,C)=\sum_{i=1}^{n}(c_i-U_i)^2I(c_i>U_i)+(c_i-L_i)^2I(c_i < U_i)
U_i和L_i是时间序列Q的上下边界,U_i=max(q_{i-r}:q_{i+r}),L_i=min(q_{i-r}:q_{i+r})。其中r是可达到的边界,I(\cdot)是指示函数。该方法可以通过以下代码实现。
def LB_Keogh(s1,s2,r):LB_sum=0for ind,i in enumerate(s1):lower_bound=min(s2[(ind-r if ind-r>=0 else 0):(ind+r)])upper_bound=max(s2[(ind-r if ind-r>=0 else 0):(ind+r)])if i>upper_bound:LB_sum=LB_sum+(i-upper_bound)**2elif i<lower_bound:LB_sum=LB_sum+(i-lower_bound)**2return sqrt(LB_sum)
LB Keogh小界方法是线性的,而DTW则是复杂的二次方形式,这使得它在处理大量时间序列的时候非常有利。
分类与聚类
现在我们有了可靠的方法去判断两个时间序列是否相似,截下来便可以使用k-NN算法进行分类。根据经验,最优解一般出现在k=1的时候。下面就利用DTW欧氏距离的1-NN算法。在该算法中,train是时间序列示例的训练集,其中时间序列所属的类被附加到时间序列的末尾。test是相应的测试集,它所属于的类别就是我们想要预测的结果。在该算法中,对于测试集中的每一个时间序列,每一遍搜索必须遍历训练集中的所有点,从而可以找到最多的相似点。考虑到DTW算法是二次方的,计算过程会耗费非常长时间。我们可以通过LB Keogh下界方法来提高分类算法的计算速度。计算机运行LB Keogh的速度会比运行DTW的速度快很多。另外,当LBKeogh(Q,C)\leq DTW(Q,C)时,我们可以消除那些比当前最相似的时间序列不可能更相似的时间序列。这样,我们就可以消除很多不必要的DTW计算过程。
from sklearn.metrics import classification_reportdef knn(train,test,w):preds=[]for ind,i in enumerate(test):min_dist=float('inf')closest_seq=[]#print indfor j in train:if LB_Keogh(i[:-1],j[:-1],5)<min_dist:dist=DTWDistance(i[:-1],j[:-1],w)if dist<min_dist:min_dist=distclosest_seq=jpreds.append(closest_seq[-1])return classification_report(test[:,-1],preds)
下面测试一批数据。设置窗口大小为4。另外,尽管这里使用了LB Keogh下界方法和局部性约束,计算过程仍然需要几分钟。
train = np.genfromtxt('datasets/train.csv', delimiter='\t')
test = np.genfromtxt('datasets/test.csv', delimiter='\t')
print knn(train,test,4)
运行结果如下

这种方法也可用于k-mean聚类。在这种算法中,簇的数量设置为apriori,相似的时间序列会被放在一起。
import randomdef k_means_clust(data,num_clust,num_iter,w=5):centroids=random.sample(data,num_clust)counter=0for n in range(num_iter):counter+=1print counterassignments={}#assign data points to clustersfor ind,i in enumerate(data):min_dist=float('inf')closest_clust=Nonefor c_ind,j in enumerate(centroids):if LB_Keogh(i,j,5)<min_dist:cur_dist=DTWDistance(i,j,w)if cur_dist<min_dist:min_dist=cur_distclosest_clust=c_indif closest_clust in assignments:assignments[closest_clust].append(ind)else:assignments[closest_clust]=[]#recalculate centroids of clustersfor key in assignments:clust_sum=0for k in assignments[key]:clust_sum=clust_sum+data[k]centroids[key]=[m/len(assignments[key]) for m in clust_sum]return centroids
再用这种算法测试一下数据:
train = np.genfromtxt('datasets/train.csv', delimiter='\t')
test = np.genfromtxt('datasets/test.csv', delimiter='\t')
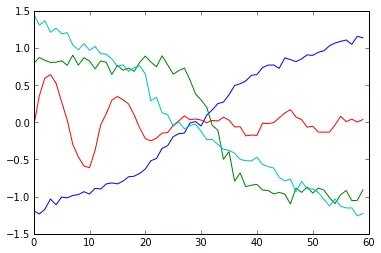
data=np.vstack((train[:,:-1],test[:,:-1]))import matplotlib.pylab as pltcentroids=k_means_clust(data,4,10,4)
for i in centroids:plt.plot(i)plt.show()
结果如图
代码
所有用到的代码都可以在my gitHub repo找到。
转载:https://www.cnblogs.com/think90/articles/11975242.html
相关文章:

对时序数据进行分类与聚类
我在最近的工作中遇到了一个问题,问题是我需要根据银行账户在一定时间内的使用信息对该账户在未来的一段时间是否会被销户进行预测。这是一个双元值的分类问题,只有两种可能,即会被销户和不会被销户。针对这个问题一般来说有两种解决策略。 …...
Win10如何找回图片查看器
近期有小伙伴反映在将Win10升级之后发现电脑自带的图片查看器没有了,这是怎么回事,该怎么找回呢,下面小编就给大家详细介绍一下Win10找回图片查看器的方法,有需要的小伙伴快来和小编一起阅读看看吧。 win10找回windows照片查看器…...

【脑机接口】基于运动想象的康复指导在脑卒中偏瘫患者中的应用
【摘要】 目的 探讨运动想象康复指导对脑卒中偏瘫患者的康复效果及意义。 方法 将 60例脑卒中偏瘫患者随机分为观察组(n31)和对照组(n29),对照组的康复训练指导采用讲解示范法,观察组采用运动想象法 。比较两组 患者 的运 动功能 、日常生活 活动能力及 …...

vue-cli中vuex下$store”未在实例上定义
这里写目录标题 一、版本的问题二、vuex中的代码 一、版本的问题 vuex版本不对,获取不到store,vue默认vue3版本,vuex默认vuex4版本,vuex4只能在vue3中使用,在vue2中能使用vuex3,那么不能默认下载最新的版本 npm instal…...
12.1 BSW WatchDog功能的配置和实现)
AutoSAR配置与实践(实践篇)12.1 BSW WatchDog功能的配置和实现
AutoSAR配置与实践(实践篇)12.1 BSW WatchDog功能的配置和实现 BSW WatchDog功能的配置和实现一、Wdg监控需求二、WdgM状态管理原理2.1 WdgM状态管理中的配置项和层次关系2.2 SE 本地状态(Local Status)管理2.3 全局状态(Global Status)管理三、Alive/ Deadline/ Program Flo…...

【UI自动化测试】Jenkins配置
前一段时间帮助团队搭建了UI自动化环境,这里将Jenkins环境的一些配置分享给大家。 背景: 团队下半年的目标之一是实现自动化测试,这里要吐槽一下,之前开发的测试平台了,最初的目的是用来做接口自动化测试和性能测试&…...

C#使用DataTable的Select方法来选择特定的字段
在C#中,可以使用DataTable的Select方法来选择特定的字段。要选择特定的字段,可以使用Select方法的参数来指定要返回的列的名称,然后将结果存储在一个新的DataTable中。以下是一个示例: using System; using System.Data; class …...

总结梳理HTTP状态码
前端开发中和后端联调时总会遇到一些状态码的问题,本文用于介绍一些常见的状态码,以及遇到这些状态码应该如何进行排查。 400 Bad Request - 请求无效。 表示客户端发送的请求存在语法错误,服务器无法理解或处理该请求的语法或参数。这通常…...

MySQL 8.0(winx64)安装笔记
一、背景 从MySQL 5.6到5.7,再到8.0,版本的跳跃不可谓不大。安装、配置的差别也不可谓不大,特此备忘。 二、过程 (1)获取MySQL 8.0社区版(MySQL Community Server) 从 官网 字样 “MySQL …...

vue封装wangEditor
components下面创建WangEditor.vue <template><div><toolbarstyle"border-bottom: 1px solid #ccc":editor"editor":defaultConfig"toolbarConfig":mode"mode"/><editorstyle"height: 500px; overflow-y: …...
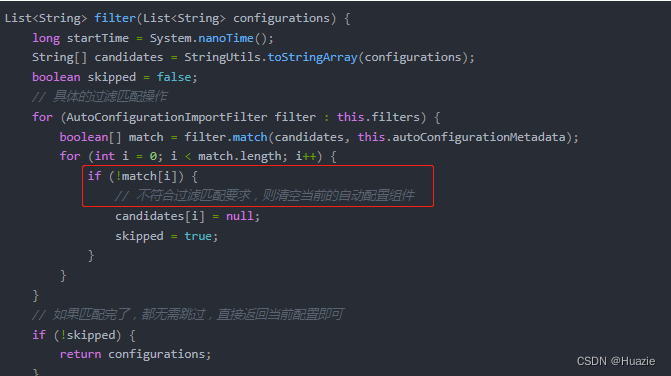
【Spring Boot 源码学习】深入 FilteringSpringBootCondition
走近 AutoConfigurationImportFilter 引言往期内容主要内容1. match 方法2. ClassNameFilter 枚举类3. filter 方法 总结 引言 前两篇博文笔者带大家从源码深入了解了 Spring Boot 的自动装配流程,其中自动配置过滤的实现由于篇幅限制,还未深入分析。 …...

docker 笔记6:高级篇 DockerFile解析
目录 1.是什么? 2.构建三步骤 3.DockerFile构建过程解析 3.1 Dockerfile内容基础知识 3.2Docker执行Dockerfile的大致流程 总结 4.DockerFile常用保留字指令 5.案例:自定义镜像 5.1 要求: Centos7镜像具备vimifconfigjdk8 5.2编写 5…...
微信小程序navigateTo进入页面后返回原来的页面需要携带数据回来
需求 如图:点击评论后会通过wx.navigateTo进入到评论页面,评论完返回count给原页面,重新赋值实现数量动态变化,不然要刷新这个页面才会更新最新的评论数量。 实现方式: 在评论页面通过wx.setStorageSync(‘data’…...

Python照片压缩教程详解
介绍 在日常的编程工作中,我们经常需要处理图像,例如上传、下载、显示、编辑等。有时候,我们需要对图像进行压缩,以减少占用的空间和带宽,提高加载速度和用户体验。那么,如何用Python来实现图像压缩呢&…...

软路由的负载均衡设置:优化网络性能和带宽利用率
在现代网络环境中,提升网络性能和最大化带宽利用率至关重要。通过合理配置软路由IP的负载均衡设置,可以有效地实现这一目标,并提高整体稳定性与效果。本文将详细介绍如何进行软路由IP的负载均衡设置,从而优化网络表现、增加带宽利…...

CH06_第一组重构(上)
提取函数(Extract Function |106) 曾用名:提炼函数(Extract Function) 反向重构:内联函数(115) 示例代码 function printOwing(invoice) {printBanner();let outstanding calcul…...

RHCSA-VMware Workstation Pro-Linux基础配置命令
1.代码命令 1.查看本机IP地址: ip addr 或者 ip a [foxbogon ~]$ ip addre [foxbogon ~]$ ip a 1:<Loopback,U,LOWER-UP> 为环回2网卡 2: ens160: <BROADCAST,MULTICAST,UP,LOWER_UP>为虚拟机自身网卡 2.测试网络联通性: [f…...

YOLO-NAS详细教程-姿势估计实现
姿势估计是一项计算机视觉任务,涉及估计图像或视频中物体或人的位置和方向。它通常涉及识别特定的关键点或身体部位(例如关节),并确定它们的相对位置和方向。姿势估计有许多应用,包括机器人、增强现实、人机交互和运动分析。 自上而下和自下而上是姿态估计中两种常用的方法…...
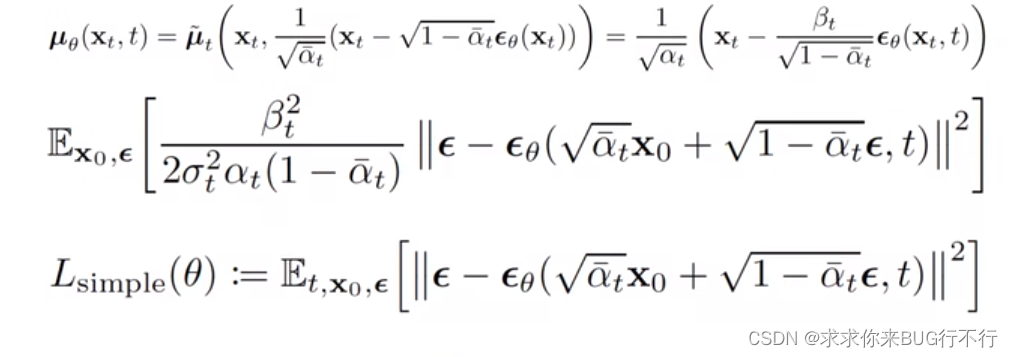
【扩散模型 李宏毅B站教学以及基础代码运用】
李宏毅教学视频: Link1 B站DDPM公式推导以及代码实现: Link2 这个视频里面有论文里面的公式推导,并且1小时10分开始讲解实例代码。 文章目录 扩散模型概念:Diffusion Model工作原理:影像生成模型本质上的共同目标B站…...
SpringBoot隐藏文件
1.设置 2.输入file Types 3.点击忽略文件或者文件夹 4.成功...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
