P2719 搞笑世界杯 (期望dp
#include <bits/stdc++.h>
using namespace std;
using VI = vector<int>;double dp[2000][2000];
int n;
//求dp[2][0]
//dp[0][2]
//期望dp要从终末态,向起始态转移
//dp[a][b] - > dp[a][b-1] or dp[a-1][b]
//dp[a][b] = 1/2 * dp[a][b+1] + 1/2 * dp[a+1][b]
int main(){cin>>n;n/=2;dp[n][n] = 1;for(int i = n ; i >= 1 ; i--){for(int j = n ; j >= 1 ; j--){dp[i][j-1] += dp[i][j] / 2.0;dp[i-1][j] += dp[i][j] / 2.0;}}double res = 0;for(int i = 2; i <= n ; i++){res += dp[i][0] + dp[0][i];} printf("%.4f" , res);}考虑一种票全部卖完,另一种有大于等于2 张的所有情况都为合理情况
dp[i][j] 可以 等概率的转移到 dp[i-1][j] 和 dp[j][i-1]
相关文章:

P2719 搞笑世界杯 (期望dp
#include <bits/stdc.h> using namespace std; using VI vector<int>;double dp[2000][2000]; int n; //求dp[2][0] //dp[0][2] //期望dp要从终末态,向起始态转移 //dp[a][b] - > dp[a][b-1] or dp[a-1][b] //dp[a][b] 1/2 * dp[a][b1] 1/2 * dp…...

spring cloud新版本使用loadbalancer替代Ribbon
Nacos 2021 不再集成 Ribbon,建议使用spring cloud loadbalancer 引入 一、简单使用 引入依赖spring cloud loadbalancer <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-loadbalancer<…...

【Git-Exception】Git报错:fatal: unable to auto-detect email address
报错信息: *** Please tell me who you are. Run git config --global user.email “youexample.com” git config –global user.name “Your Name” to set your account’s default identity. Omit --global to set the identity only in this repository. fatal…...

JVM性能优化 —— 类加载器,手动实现类的热加载
一、类加载的机制的层次结构 每个编写的”.java”拓展名类文件都存储着需要执行的程序逻辑,这些”.java”文件经过Java编译器编译成拓展名为”.class”的文件,”.class”文件中保存着Java代码经转换后的虚拟机指令,当需要使用某个类时&#…...

SSH连接MobaXterm
IT常用软件的安装 ssh连接MobaXterm详细使用教程 数据库Navicat安装:https://www.jianshu.com/p/2494e02caf63 java SE安装 https://www.oracle.com/java/technologies/javase/javase-jdk8-downloads.html windows安装pip https://www.cnblogs.com/NanShan2016/…...

本地虚机Jumpserver使用域名访问报错 使用IP+端口没有错误
背景: 我在本地Windows VMware 15的环境中部署了CentOS7.5,下载jumpserver-offline-installer-v2.28.1-amd64-138.tar.gz并安装部署。 需求: 1、能使用http:ip访问堡垒机。达成; 2、能使用http:域名访问堡垒机。达成ÿ…...
----数据库设计基础)
备战计算机二级公共基础知识(五)----数据库设计基础
数据库设计基础 目录 数据库设计基础 数据库的基本概念:数据库,数据库管理系统,数据库系统 数据模型,实体联系模型及 E-R 图,从 E-R 图导出关系…...
【excel密码】excel文件加密方法总结:
想要给Excel文件进行加密,方法有很多,今天分享三种Excel加密方法给大家。 打开密码 设置了打开密码的excel文件,打开文件就会提示输入密码才能打开excel文件,只有输入了正确的密码才能打开并且编辑文件,如果密码错误…...

MySQL之用户管理
用户 用户信息 MySQL中的用户,都存储在系统数据库mysql的user表中 ps: host: 表示这个用户可以从哪个主机登陆,如果是localhost,表示只能从本机登陆 user: 用户名 authentication_string: 用户…...

伪静态web.config常见规则写法与参数介绍说明
伪静态web.config常见规则写法与参数介绍说明. 示例1: <?xml version"1.0" encoding"UTF-8"?> <configuration><system.webServer><rewrite><rules><rule name"规则 1" stopProcessing"tru…...

使用kubasz快速搭建Kubernetes集群
Kubernetes安装 Kubernetes 也称为 K8s,是用于自动部署、扩缩和管理容器化应用程序的开源系统。ansible是新出现的自动化运维工具,基于Python开发,集合了众多运维工具(puppet、chef、func、fabric)的优点,实现了批量系统配置、批量程序部署、批量运行命令等功能。使用ans…...

php常用加密算法大全aes、3des、rsa等
目录 一、可解密加解密算法 1、aes 加解密算法 2、旧3des加解密方法 3、新3des加解密方法 4、rsa公私钥加解密、签名验签方法 5、自定义加密算法1 6、自定义加密算法2 7、自定义加密算法3 二、不可解密加密算法 1、md5算法 2、crypt算法 3、sha1算法 5、hash 算…...

ubuntu22.04搭建verilator仿真环境
概述 操作系统为 Ubuntu(22.04.2 LTS),本次安装verilator开源verilog仿真工具,进行RTL功能仿真。下面构建版本为5.008的verilator仿真环境。先看一下我系统的版本: 安装流程 安装依赖 sudo apt-get install git perl python3 make autoc…...

python中如何使用正则表达匹配\本身?(文末赠书)
点击上方“Python爬虫与数据挖掘”,进行关注 回复“书籍”即可获赠Python从入门到进阶共10本电子书 今 日 鸡 汤 将军向宠,性行淑均。 大家好,我是皮皮。 一、前言 前几天在Python钻石群【空】问了一个Python正则表达式的问题,一起…...

Linux学习之MySQL连接查询
接上一篇 连接查询 连接查询也中多表查询,常用于查询来自于多张表的数据,通过不同的连接方式把多张表组成一张新的临时表,再对临时表做数据处理。 #表基础信息,内容可从上一篇博客中查看 mysql> desc departments; ---------…...

【Hello Algorithm】二叉树相关算法
本篇博客介绍:介绍二叉树的相关算法 二叉树相关算法 二叉树结构遍历二叉树递归序二叉树的交集非递归方式实现二叉树遍历二叉树的层序遍历 二叉树难题二叉树的序列化和反序列化lc431求二叉树最宽的层二叉树的后继节点谷歌面试题 二叉树结构 如果对于二叉树的结构还有…...
ExpressLRS开源代码之工程结构
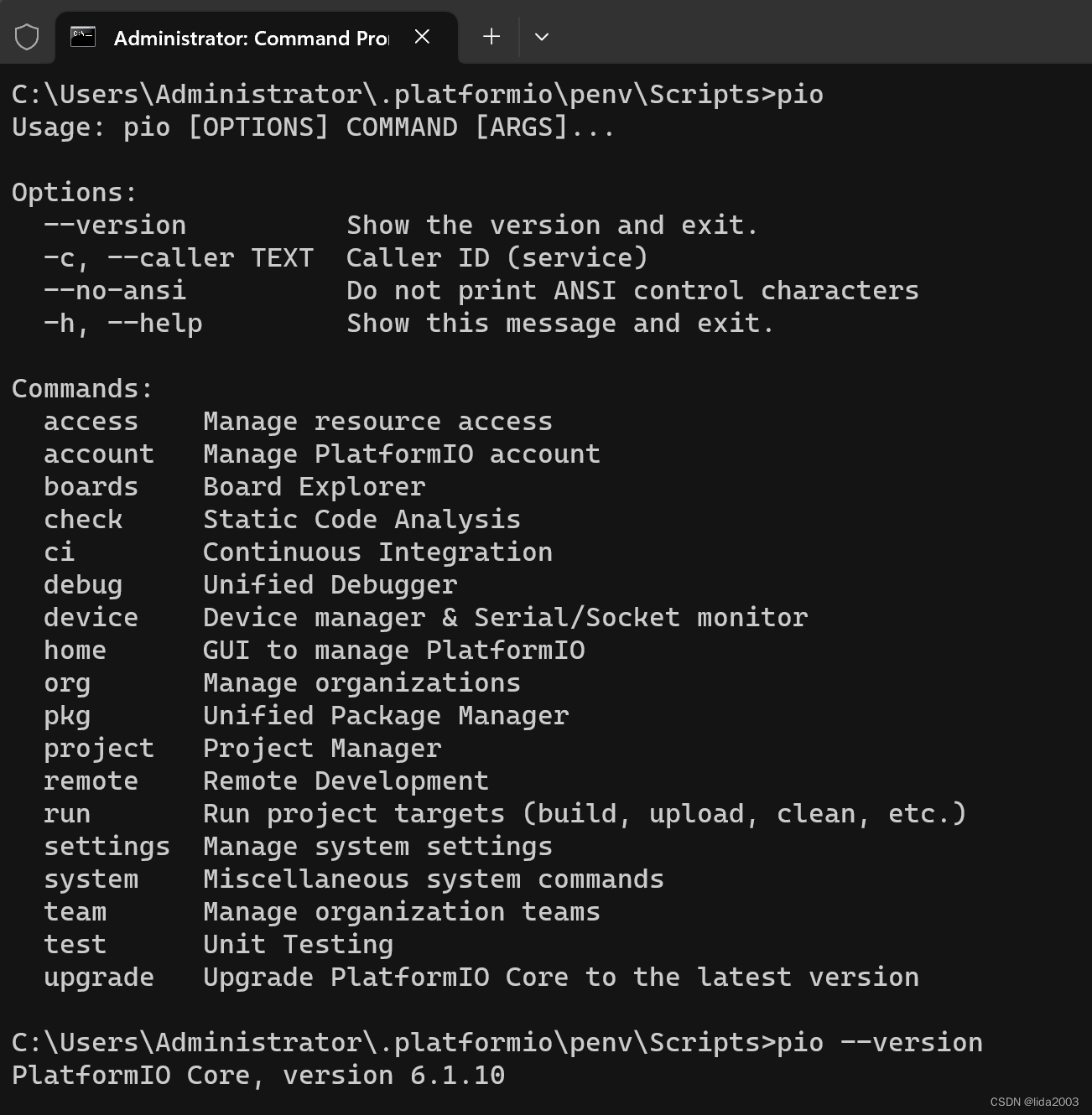
ExpressLRS开源代码之工程结构 1. 源由2. 工程3. 开发环境安装4. pio命令5. ExpressLRS配置6. 硬件认证过程7. 参考资料 1. 源由 ExpressLRS开源代码基于Arduino框架设计,在所支持的硬件环境下,提供900/2400发射机和接收机硬件方案。 该设计提供了一个…...
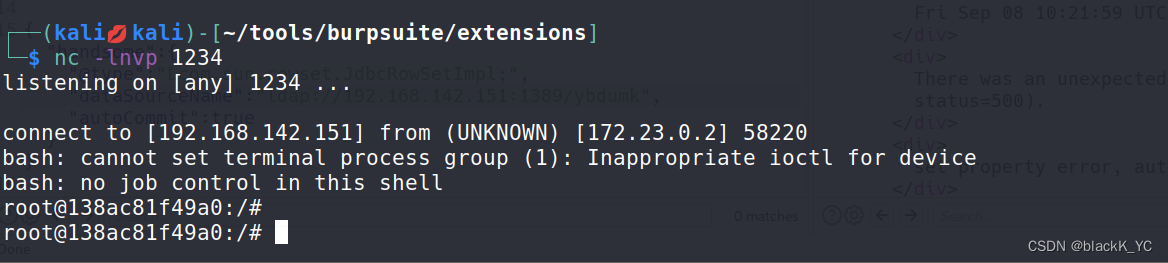
fastjson 1.2.24 反序列化导致任意命令执行漏洞复现
拉取docker容器 访问并抓包 修改为POST 方式,文件类型改为json格式,发送json数据包,发送成功 这里安装一个bp的插件 使用安装的插件 可以看到,插件告诉我们这里有漏洞,并且提供了POC 既然我们发现有 rmi ,…...
 rownum、rowid、oid)
探秘MySQL三个神秘隐藏列(mysql三个隐藏列) rownum、rowid、oid
探秘MySQL三个神秘隐藏列 MySQL是一款流行的关系型数据库管理系统,被广泛应用于Web应用程序开发和数据存储。然而,MySQL也有一些神秘的隐藏列,这些隐藏列可以帮助我们更好地管理和查询数据。 接下来,我们将探秘MySQL三个神秘隐藏…...
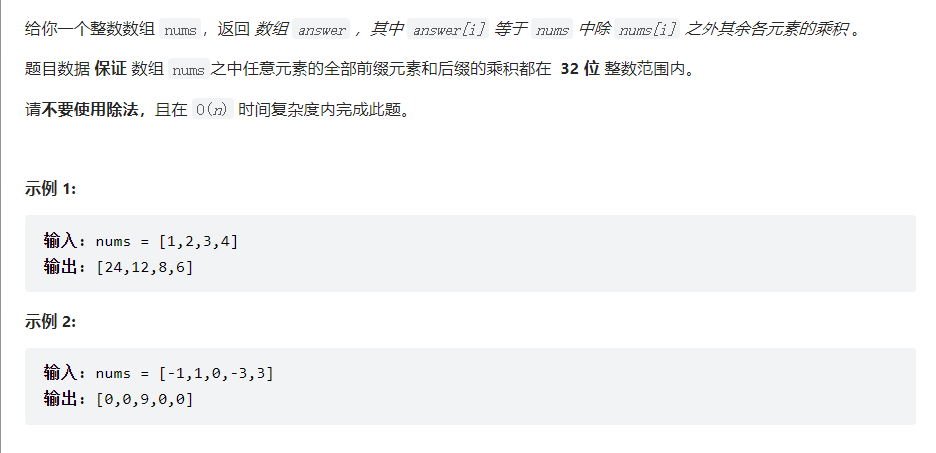
leetcode刷题--数组类
文章目录 1. 485 最大连续1的个数2. 495 提莫攻击3. 414 第三大的数4. 628 三个数的最大乘积5. 645 错误的集合6. 697 数组的度7. 448 找到所有数组中消失的数字9. 41 缺失的第一个正数10. 274 H指数11. 453 最小操作次数使得数组元素相等12. 665 非递减数列13. 283 移动零14. …...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
