说说BTree和B+Tree
分析&回答
B+树索引是B+树在数据库中的一种实现,是最常见也是数据库中使用最为频繁的一种索引。B+树中的B代表平衡(balance),而不是二叉(binary),因为B+树是从最早的平衡二叉树演化而来的。
接下来我们一步步了解 二叉查找树 > 平衡二叉树(AVLTree) > 平衡多路查找树(B-Tree) > B+树。
二叉查找树
二叉树具有以下性质:左子树的键值小于根的键值,右子树的键值大于根的键值。

要想效率高,平衡不可少。所以我们需要平衡二叉树,或称AVL树。
平衡二叉树(AVLTree)
平衡二叉树(AVL树)在符合二叉查找树的条件下,还满足任何节点的两个子树的高度最大差为1。下面的两张图片,左边是AVL树,它的任何节点的两个子树的高度差<=1;右边的不是AVL树,其根节点的左子树高度为3,而右子树高度为1;

如果在AVL树中进行插入或删除节点,可能导致AVL树失去平衡,这种失去平衡的二叉树可以概括为四种姿态:LL(左左)、RR(右右)、LR(左右)、RL(右左)。它们的示意图如下:

这四种失去平衡的姿态都有各自的定义:
- LL:LeftLeft,也称“左左”。插入或删除一个节点后,根节点的左孩子(Left Child)的左孩子(Left Child)还有非空节点,导致根节点的左子树高度比右子树高度高2,AVL树失去平衡。
- RR:RightRight,也称“右右”。插入或删除一个节点后,根节点的右孩子(Right Child)的右孩子(Right Child)还有非空节点,导致根节点的右子树高度比左子树高度高2,AVL树失去平衡。
- LR:LeftRight,也称“左右”。插入或删除一个节点后,根节点的左孩子(Left Child)的右孩子(Right Child)还有非空节点,导致根节点的左子树高度比右子树高度高2,AVL树失去平衡。
- RL:RightLeft,也称“右左”。插入或删除一个节点后,根节点的右孩子(Right Child)的左孩子(Left Child)还有非空节点,导致根节点的右子树高度比左子树高度高2,AVL树失去平衡。 AVL树失去平衡之后,可以通过旋转使其恢复平衡。
平衡多路查找树(B-Tree)
B-Tree是为磁盘等外存储设备设计的一种平衡查找树。因此在讲B-Tree之前先了解下磁盘的相关知识。
系统从磁盘读取数据到内存时是以磁盘块(block)为基本单位的,位于同一个磁盘块中的数据会被一次性读取出来,而不是需要什么取什么。
InnoDB存储引擎中有页(Page)的概念,页是其磁盘管理的最小单位。InnoDB存储引擎中默认每个页的大小为16KB,可通过参数innodb_page_size将页的大小设置为4K、8K、16K,在MySQL中可通过如下命令查看页的大小: mysql> show variables like 'innodb_page_size';
而系统一个磁盘块的存储空间往往没有这么大,因此InnoDB每次申请磁盘空间时都会是若干地址连续磁盘块来达到页的大小16KB。InnoDB在把磁盘数据读入到磁盘时会以页为基本单位,在查询数据时如果一个页中的每条数据都能有助于定位数据记录的位置,这将会减少磁盘I/O次数,提高查询效率。
B-Tree结构的数据可以让系统高效的找到数据所在的磁盘块。为了描述B-Tree,首先定义一条记录为一个二元组[key, data] ,key为记录的键值,对应表中的主键值,data为一行记录中除主键外的数据。对于不同的记录,key值互不相同。
一棵m阶的B-Tree有如下特性:
- 每个节点最多有m个孩子。
- 除了根节点和叶子节点外,其它每个节点至少有Ceil(m/2)个孩子。
- 若根节点不是叶子节点,则至少有2个孩子
- 所有叶子节点都在同一层,且不包含其它关键字信息
- 每个非终端节点包含n个关键字信息(P0,P1,…Pn, k1,…kn)
- 关键字的个数n满足:ceil(m/2)-1 <= n <= m-1
- ki(i=1,…n)为关键字,且关键字升序排序。
- Pi(i=1,…n)为指向子树根节点的指针。P(i-1)指向的子树的所有节点关键字均小于ki,但都大于k(i-1)
B-Tree中的每个节点根据实际情况可以包含大量的关键字信息和分支,如下图所示为一个3阶的B-Tree:
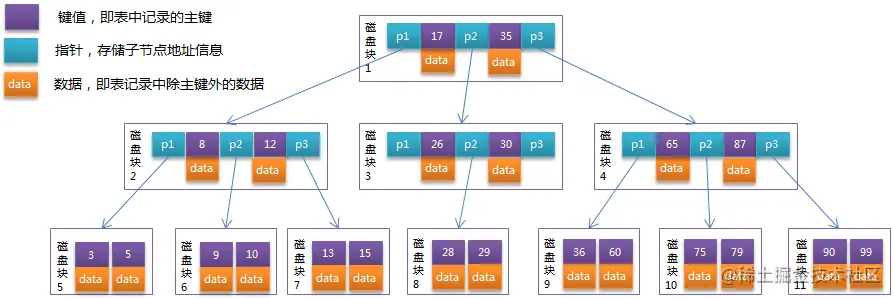
每个节点占用一个盘块的磁盘空间,一个节点上有两个升序排序的关键字和三个指向子树根节点的指针,指针存储的是子节点所在磁盘块的地址。两个关键词划分成的三个范围域对应三个指针指向的子树的数据的范围域。以根节点为例,关键字为17和35,P1指针指向的子树的数据范围为小于17,P2指针指向的子树的数据范围为17~35,P3指针指向的子树的数据范围为大于35。
模拟查找关键字29的过程:
- 根据根节点找到磁盘块1,读入内存。【磁盘I/O操作第1次】
- 比较关键字29在区间(17,35),找到磁盘块1的指针P2。
- 根据P2指针找到磁盘块3,读入内存。【磁盘I/O操作第2次】
- 比较关键字29在区间(26,30),找到磁盘块3的指针P2。
- 根据P2指针找到磁盘块8,读入内存。【磁盘I/O操作第3次】
- 在磁盘块8中的关键字列表中找到关键字29。
分析上面过程,发现需要3次磁盘I/O操作,和3次内存查找操作。由于内存中的关键字是一个有序表结构,可以利用二分法查找提高效率。而3次磁盘I/O操作是影响整个B-Tree查找效率的决定因素。B-Tree相对于AVLTree缩减了节点个数,使每次磁盘I/O取到内存的数据都发挥了作用,从而提高了查询效率。
B+树
B+Tree是在B-Tree基础上的一种优化,使其更适合实现外存储索引结构,InnoDB存储引擎就是用B+Tree实现其索引结构。
从上一节中的B-Tree结构图中可以看到每个节点中不仅包含数据的key值,还有data值。而每一个页的存储空间是有限的,如果data数据较大时将会导致每个节点(即一个页)能存储的key的数量很小,当存储的数据量很大时同样会导致B-Tree的深度较大,增大查询时的磁盘I/O次数,进而影响查询效率。在B+Tree中,所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上,而非叶子节点上只存储key值信息,这样可以大大加大每个节点存储的key值数量,降低B+Tree的高度。
B+Tree相对于B-Tree有几点不同:
- 非叶子节点只存储键值信息。
- 所有叶子节点之间都有一个链指针。
- 数据记录都存放在叶子节点中。
将上一节中的B-Tree优化,由于B+Tree的非叶子节点只存储键值信息,假设每个磁盘块能存储4个键值及指针信息,则变成B+Tree后其结构如下图所示:

通常在B+Tree上有两个头指针,一个指向根节点,另一个指向关键字最小的叶子节点,而且所有叶子节点(即数据节点)之间是一种链式环结构。因此可以对B+Tree进行两种查找运算:一种是对于主键的范围查找和分页查找,另一种是从根节点开始,进行随机查找。
可能上面例子中只有22条数据记录,看不出B+Tree的优点,下面做一个推算:
InnoDB存储引擎中页的大小为16KB,一般表的主键类型为INT(占用4个字节)或BIGINT(占用8个字节),指针类型也一般为4或8个字节,也就是说一个页(B+Tree中的一个节点)中大概存储16KB/(8B+8B)=1K个键值(因为是估值,为方便计算,这里的K取值为〖10〗^3)。也就是说一个深度为3的B+Tree索引可以维护10^3 * 10^3 * 10^3 = 10亿 条记录。
实际情况中每个节点可能不能填充满,因此在数据库中,B+Tree的高度一般都在2 ~ 4层。mysql的InnoDB存储引擎在设计时是将根节点常驻内存的,也就是说查找某一键值的行记录时最多只需要1 ~ 3次磁盘I/O操作。
数据库中的B+Tree索引可以分为聚集索引(clustered index)和辅助索引(secondary index)。上面的B+Tree示例图在数据库中的实现即为聚集索引,聚集索引的B+Tree中的叶子节点存放的是整张表的行记录数据。辅助索引与聚集索引的区别在于辅助索引的叶子节点并不包含行记录的全部数据,而是存储相应行数据的聚集索引键,即主键。当通过辅助索引来查询数据时,InnoDB存储引擎会遍历辅助索引找到主键,然后再通过主键在聚集索引中找到完整的行记录数据。
反思&扩展
平衡多路查找树恢复平衡
下面分别介绍四种失去平衡的情况下对应的旋转方法。
LL的旋转。LL失去平衡的情况下,可以通过一次旋转让AVL树恢复平衡。步骤如下:
- 将根节点的左孩子作为新根节点。
- 将新根节点的右孩子作为原根节点的左孩子。
- 将原根节点作为新根节点的右孩子。
LL旋转示意图如下:

RR的旋转:RR失去平衡的情况下,旋转方法与LL旋转对称,步骤如下:
- 将根节点的右孩子作为新根节点。
- 将新根节点的左孩子作为原根节点的右孩子。
- 将原根节点作为新根节点的左孩子。
RR旋转示意图如下:

LR的旋转:LR失去平衡的情况下,需要进行两次旋转,步骤如下:
- 围绕根节点的左孩子进行RR旋转。
- 围绕根节点进行LL旋转。
LR的旋转示意图如下:

RL的旋转:RL失去平衡的情况下也需要进行两次旋转,旋转方法与LR旋转对称,步骤如下:
- 围绕根节点的右孩子进行LL旋转。
- 围绕根节点进行RR旋转。
RL的旋转示意图如下:

喵呜面试助手:一站式解决面试问题,你可以搜索微信小程序 [喵呜面试助手] 或关注 [喵呜刷题] -> 面试助手 免费刷题。如有好的面试知识或技巧期待您的共享!
相关文章:

说说BTree和B+Tree
分析&回答 B树索引是B树在数据库中的一种实现,是最常见也是数据库中使用最为频繁的一种索引。B树中的B代表平衡(balance),而不是二叉(binary),因为B树是从最早的平衡二叉树演化而来的。 接…...

8.1.3 Bit representation and coding - 解读
这段描述定义了一些序列,并规定了它们在编码信息时的使用方式。下面是对每个序列的解析: 1. 序列X:在位持续时间的一半之后,将发生一个“暂停”。这个序列用于表示逻辑“1”。 2. 序列Y:在整个位持续时间内,…...

spring 理解
spring容器 程序启动时,会给spring容器一个清单,清单中列出了需要创建的对象以及对象依赖关系,spring容器会创建和组装好清单中的对象,然后将这些对象存放在spring容器中,当程序中需要使用的时候,可以到容…...

实战SpringMVC之CRUD
目录 一、前期准备 1.1 编写页面跳转控制类 二、实现CRUD 2.1 相关依赖 2.2 配置文件 2.3 逆向生成 2.4 后台代码完善 2.4.1 编写切面类 2.4.2 编写工具类 2.4.3 编写biz层 2.4.4 配置mapper.xml 2.4.5 编写相应接口类(MusicMapper) 2.4.6 处…...
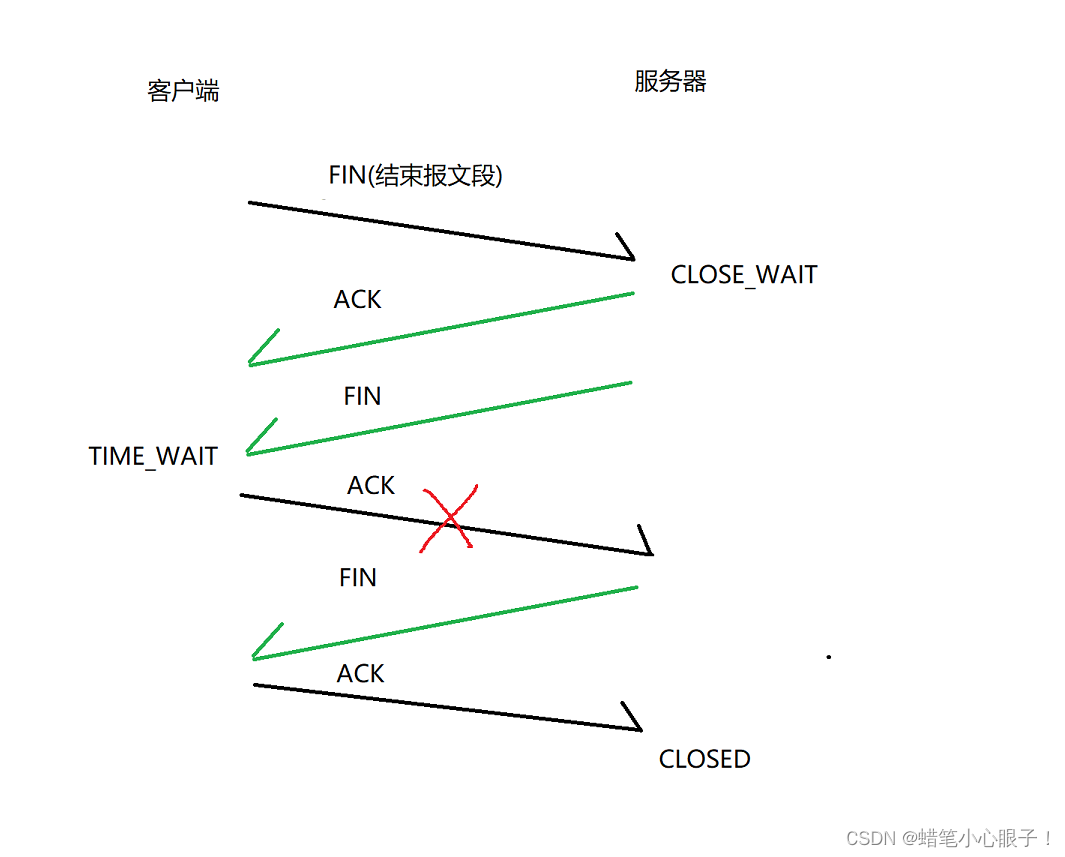
TCP机制之连接管理(三次握手和四次挥手详解)
TCP的连接管理机制描述了连接如何创建以及如何断开! 建立连接(三次握手) 三次握手的过程 所谓建立连接就是通信双方各自要记录对方的信息,彼此之间要相互认同;这里以A B双方确立男女朋友关系为例: 从图中可以看出,通信双方各自向对方发起一个"建立连接"的请求,同时…...
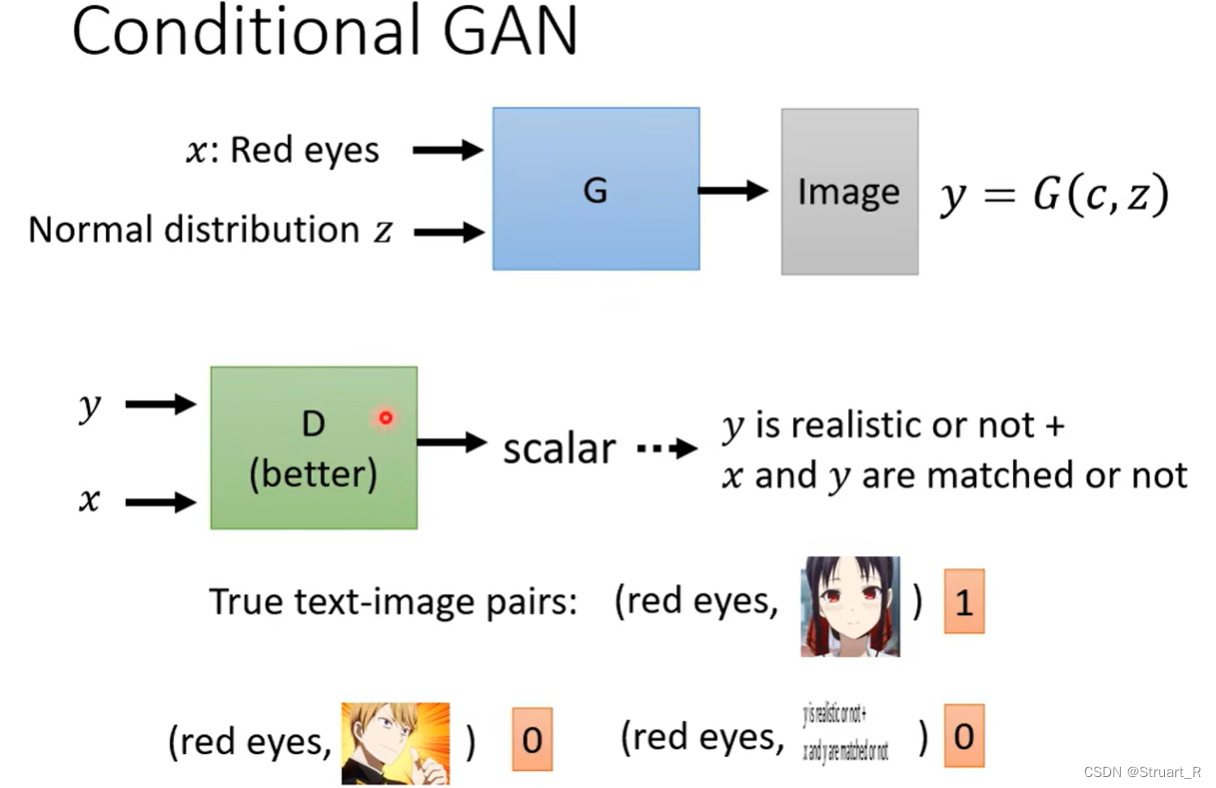
NLP(3)--GAN
目录 一、概述 二、算法过程 三、WGAN 1、GAN的不足 2、JS散度、KL散度、Wasserstein距离 3、WGAN设计 四、Mode Collapse and Mode Dropping 1、Mode Collapse 2、Mode Dropping 3、FID 四、Conditional GAN 一、概述 GAN(Generative Adversial Networ…...

无涯教程-JavaScript - IMLOG2函数
描述 IMLOG2函数以x yi或x yj文本格式返回复数的以2为底的对数。可以从自然对数计算复数的以2为底的对数,如下所示- $$\log_2(x yi)(log_2e)\ln(x yi)$$ 语法 IMLOG2 (inumber)争论 Argument描述Required/OptionalInumberA complex number for which you want the bas…...
拦截器(HandlerInterceptor)的用法)
SpringBoot复习:(61)拦截器(HandlerInterceptor)的用法
一、自定义拦截器: package cn.edu.tju.interceptor;import org.springframework.stereotype.Component; import org.springframework.web.servlet.HandlerInterceptor;import javax.servlet.http.HttpServletRequest; import javax.servlet.http.HttpServletRespo…...
【PyQT5教程】-01入门PyQT5
PyQT介绍 1.Qt 1.1 介绍 Qt(读作“cute”)是一个跨平台的C应用程序开发框架,最初由挪威公司Trolltech(现在是Qt公司的一部分)开发。Qt提供了一系列工具和类库,用于开发图形界面应用程序、命令行工具和服务…...

判断字符串s是否为字符串t的子序列
题目:给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一…...
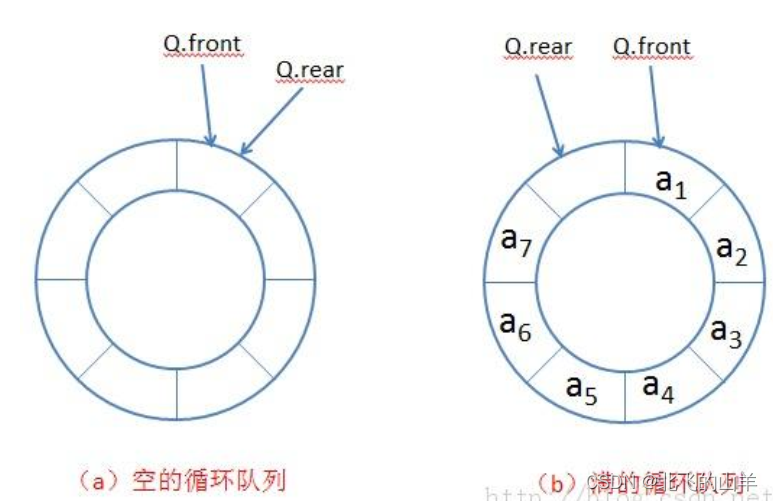
数据结构之队列的实现(附源码)
目录 一、队列的概念及结构 二、队列的实现 拓展:循环队列 三、初学的队列以及栈和队列结合的练习题 一、队列的概念及结构 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(Fi…...

[A题]2023 年全国大学生数学建模比赛思路、代码更新中.....
💥1 概述 构建以新能源为主体的新型电力系统,是我国实现“碳达峰”“碳中和”目标的一项重要措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。定日镜是塔式太阳能光热发电站(以下简称塔式电站)收集太阳能的基本组…...
Tailwind 练手项目
Tailwind 练手项目 用到的技巧 Tailwind CSS 速成 应该都提过了,我不记得这里有什么特别新的知识 整体完成图大概这样: 一个纯静态页面,没有做 JS 之类的特效,不过做了移动端适配,说实话我写到一半的时候改了不少………...
SpringMVC_SSM整合
一、回顾SpringMVC访问接口流程 1.容器加载分析 容器分析 手动注册WebApplicationContext public class ServletConfig extends AbstractDispatcherServletInitializer {Overrideprotected WebApplicationContext createServletApplicationContext() {//获取SpringMVC容器An…...
【操作系统】电脑上没有IIS怎么办
文章目录 前言一、查看二、解决 前言 有的新机刚开始在计算机-管理-服务下没有IIS网络服务怎么办。 一、查看 桌面计算机/此电脑 鼠标右键:管理 服务和应用 发现没有IIS 二、解决 控制面板 程序和功能 启动或关闭Windows功能 IIS相关的所有功能选中ÿ…...

【vue】vue项目中批量下载文件并打压缩包
前言 一开始用的是循环单个文件下载,即从后台获取到文件url列表,循环对每个url单独进行下载,这样的问题是每调用一次下载,浏览器都会进行“另存为”的弹框,很麻烦!!! 关闭“下载前…...

Linux中的软件管家——yum
目录 编辑 一,软件安装的方式 二,对yum的介绍 1.yum的作用 2,yum的库 三,yum下载软件的操作 1.yumlist 2.yuminstall 3.yumremove 四,yum源的转换 一,软件安装的方式 软件安装的方式大概分为三种…...
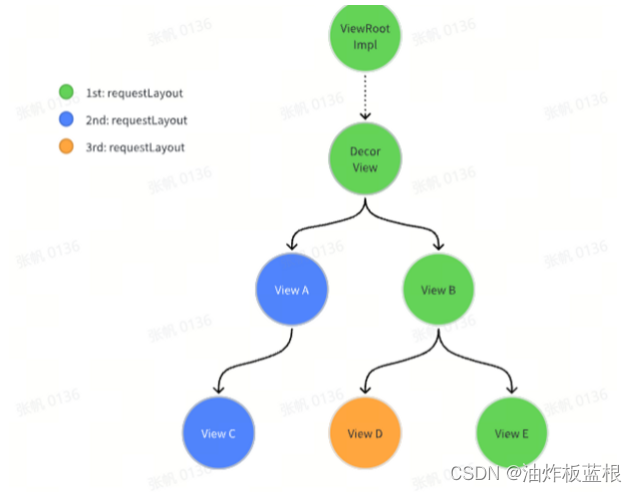
安卓绘制原理概览
绘制原理 Android 程序员都知道 Android 的绘制流程分为 Measure、Layout、Draw 三步骤,其中 Measure 负责测量 View 的大小Layout 负责确定 View 的位置Draw 负责将 View 画在屏幕上 由 ViewRootImpl 实现的 performTraversal 方法是 Measure、layout、draw 的真正…...

接口测试工具开发文档
1 开发规划 1.1 开发人员 角 色 主要职责 负责模块 人员 备注 n xxx模块 xxx 1.2 开发计划 <附开发计划表> 1.3 开发环境和工具 开发工具 工具 作用 Notepad 编辑器 Perl 解释器 2 总体设计 设计思路:因为测试app和server。首先必须…...

面试题速记:JavaScript有哪些数据类型,它们的区别是?
JavaScript有哪些数据类型,它们的区别? JavaScript共有八种数据类型,分别是 Undefined、Null、Boolean、Number、String、Object、Symbol、BigInt。 其中 Symbol 和 BigInt 是ES6 中新增的数据类型: ●Symbol 代表创建后独一无二…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
