算法之位运算
前言
位运算在我们的学习中占有很重要的地位,从二进制中数的存储等都需要我们进行位运算
一、位运算复习
1.位运算复习
按位与(&):如果两个相应的二进制位都为1,则该位的结果值才为1,否则为0
按位或( | ):如果两个相应的二进制位中有一个为1,则该位的结果值为1,否则为0
按位异或( ^ ):如果两个相应的二进制位值相同,则该位的结果值为0,否则为1
按位取反( ~ ):对二进制数按位取反,即0变为1,1变为0

其中我们使用最多的为异或操作, 异或操作又可以称为无进位相加。

2.常见的位操作
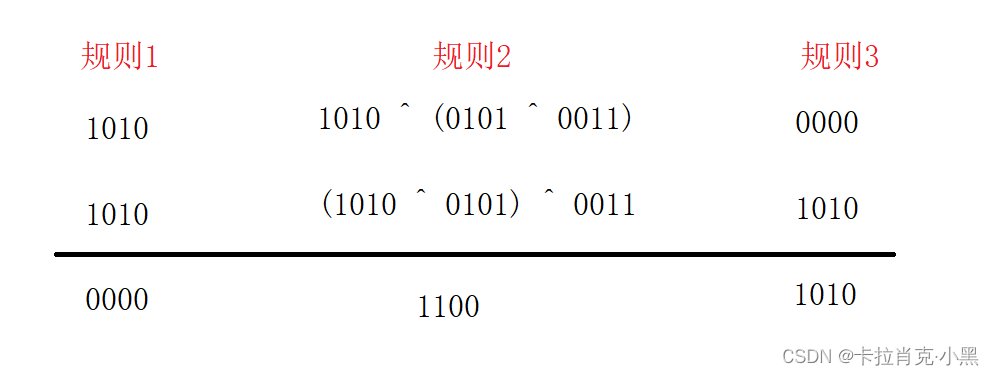
1.异或的运算规则
1. 两个相同的数异或结果为0
2. 异或满足交换律
3. 任何数异或0都为那个数本身
2.获得一个数的相反数
这个数取反加1为这个数的相反数,即( -num = (~num + 1) )

3.获得一个数中二进制位最右侧的1
这个数和它的相反数按位与,即( num &= -num)

其他的操作我们在下面补充
二、位运算练习
1.不创建第三变量进行交换两个数的值
void Swap()
{int a = 10;int b = 20;printf("交换前:a = %d,b = %d\n", a, b);a = a ^ b;b = a ^ b;a = a ^ b;printf("交换后:a = %d,b = %d\n", a, b);
}
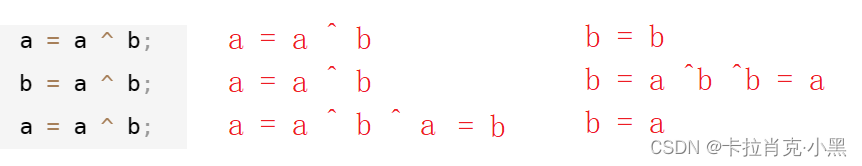
此时用的是相同的数异或为0,0异或任何数都为那个数
注意,异或操作值可以相同,但不可以对同一块空间的值进行异或,否则会变为0,比如同时对a进行异或。
测试结果:

相关练习
2.不使用比较操作返回较大的数
void Compare()
{int a = 10;int b = 20;int c = a - b;int sya = ((a >> 31) & 1);//获得a的符号位int syb = ((b >> 31) & 1);//获得b的符号位int syc = ((c >> 31) & 1);//获得c的符号位int dif = sya ^ syb;//判断a和b的符号位是否相同//符号位相同则不会产生溢出if (dif == 0){if (syc == 1){printf("最大值为:%d\n", b);}else{printf("最大值为:%d\n", a);}}//可能会产生溢出else{if (sya == 1 && syb == 0){printf("最大值为:%d\n", b);}else{printf("最大值为:%d\n", a);}}
}
测试结果:
注意,两个数相加或者相减都可能产生溢出的情况,下面以char为例:
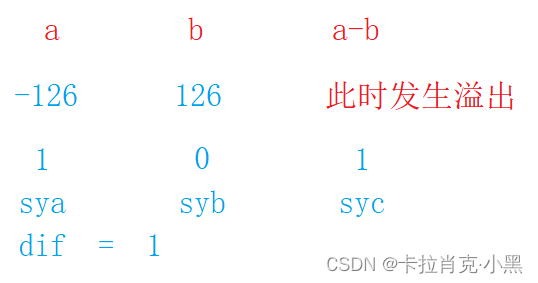
又比如:

所以这个需要我们进行判断是否会进行溢出,这个直接返回两个数相减的结果是否大于0在溢出情况下并不适用。
练习操作
3.不使用加减乘除等符号进行相应的操作
1.加法
//加法
int Add(int a, int b)
{int sum = a;while (b != 0){sum = a ^ b;//获得要进行进位的位置b = (a & b) << 1;a = sum;}
}

测试结果:

我们异或是不进位相加,所以下面两个数进行与是找到这两数都为1的位置,进行右移在异或相当于向前进1。
2.减法
//减法
int Sub(int a, int b)
{//获得b的相反数int sum = Add(~b, 1);//a和b的相反数进行相加sum = Add(a, sum);return sum;
}
测试结果:

在这里我们可以同通过我们的add函数来得到我们的所要的相反数,原理就是我们的按位取反加1得到
3.乘法
//乘法
int Mul(int a, int b)
{int sum = 0;while (b != 0){if ((b & 1) != 0)//b当前最右侧的是否为1{sum = Add(sum, a);}//模拟相乘的过程a <<= 1;//a进行右移b >>= 1;//b进行左移}return sum;
}
测试结果:

原理:二进制的乘法和十进制的乘法相同,在这里我们把十进制相乘转换为二进制相乘,我们可以通过移位来获得每个相加的数
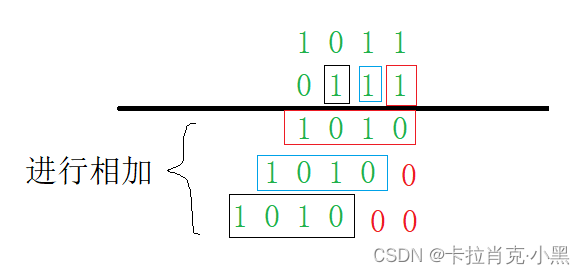
4.除法
//除法
int div(int a, int b)
{int x = a < 0 ? Add(~a, 1) : a;int y = b < 0 ? Add(~b, 1) : b;int sum = 0;int i = 0;//从第31位开始进行判断for (i = 31; i > -1; i = Sub(i, 1)){if ((x >> i) >= y){sum |= (1 << i);x = Sub(x, y << i);}}return ((a < 0) ^ (b < 0)) ? Add(~sum, 1) : sum;
}
int Div(int a, int b)
{if (b == 0){//0为除数,结束程序exit(-1);}if (a == INT_MIN && b == INT_MIN){return 1;}else if (b == INT_MIN){return 0;}else if (a == INT_MIN){int sum = div(Add(a, 1), b);sum = Add(sum, div(Sub(a, Mul(sum, b)), b));return sum;}else{return div(a, b);}
}
测试结果:

原理:

注意:移动时要注意溢出情况,和除数是否为0。
4.整数二进制中1的个数
void Sum1()
{int a = 20;int sum = 0;while (a != 0){a &= (a - 1);sum++;}printf("1的个数为%d个\n", sum);
}
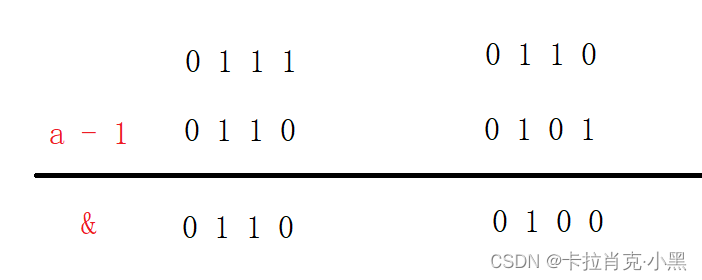
从上面可以看出我们的( a &= (a - 1) )操作是为了消除1
测试结果:
题目练习
5.在其他数都出现两次的数组中找出现一次的一个数
void Single_num()
{int arr[] = { 1,1,2,2,3,4,4,5,5,6,6 };int sum = 0;int i = 0;for (i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){sum ^= arr[i];}printf("出现一次的数%d\n", sum);
}
这个就是我们使用的交换律,和两个相同的数异或结果为0
测试结果:

练习题目
6.在其他数都出现两次的数组中找出现一次的两个数
void two_Single_num()
{int arr[] = { 1,1,2,2,3,4,5,5,6,6 };int sum = 0;int i = 0;for (i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){//找到这两个出现一次的数sum ^= arr[i];}//获得这两数异或结果最右侧的1,这个1也是这两个数不相同的位置int sum1 = sum & (~sum + 1);int sum2 = 0;for (i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){//&的优先级低于 ==//把和这个不相同的一位的值进行按位与,如果结果为0;则可以分为1组if ((sum1 & arr[i]) == 0){//得到的为其中的一位sum2 ^= arr[i];}}printf("出现一次的数%d %d\n", sum^sum2,sum2);
}
测试结果:


题目练习
7.在其他数都出现K次的数组中找出现一次的数
void k_Single_num()
{int arr[] = { 5, 4, 1, 1, 5, 1, 5 };int k = 3; int x = 0;int a[32] = { 0 };for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){//把数组中的数的每个进制位都进行相加x = arr[i];for (int j = 31; j >= 0; j--) {if (x & 1)a[j]++;x >>= 1;}}x = 0;for (int i = 0; i < 32; i++) {//对我们相加的值的每一个进制位进行相应的取模运算就是我们所要的值了x <<= 1;x += a[i] % k;}printf("%d\n", x);
}
测试结果:

原理:

我们可以看到在我们第i位置的值为((a[i] + b[i]) % 5),同理,在K进制中的两个数在i位上的无进位相加结果位((a[i] + b[i]) % K),所以k个相同的K进制位相加,那么相加后的结果每一位都为0。所以我们把出现的次数设置成相应的K进制位,最后把相加的结果转化为10进制就是我们所需要的值。
题目练习
总结
位运算还有许多的题目,大家可以在下面找着练习一下。
相关文章:

算法之位运算
前言 位运算在我们的学习中占有很重要的地位,从二进制中数的存储等都需要我们进行位运算 一、位运算复习 1.位运算复习 按位与(&):如果两个相应的二进制位都为1,则该位的结果值才为1,否则为0 按位或( | ):如果…...
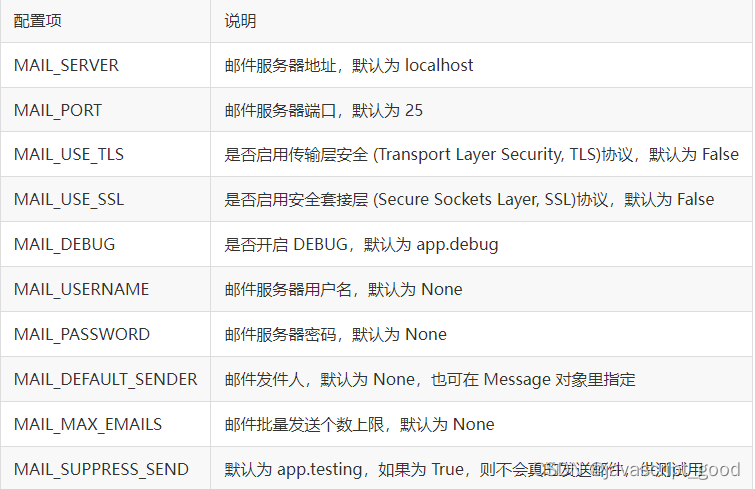
flask使用Flask-Mail实现邮件发送
Flask-Mail可以实现邮件的发送,并且可以和 Flask 集成,让我们更方便地实现此功能。 1、安装 使用pip安装: $ pip install Flask-Mail或下载源码安装: $ git clone https://github.com/mattupstate/flask-mail.git $ cd flask-…...
React refers to UMD global, but the current file is a module vite初始化react项目
vite搭建react项目 初始化项目 npm create vite 在执行完上面的命令后,npm 首先会自动下载create-vite这个第三方包,然后执行这个包中的项目初始化逻辑。输入项目名称之后按下回车,此时需要选择构建的前端框架: ✔ Project na…...
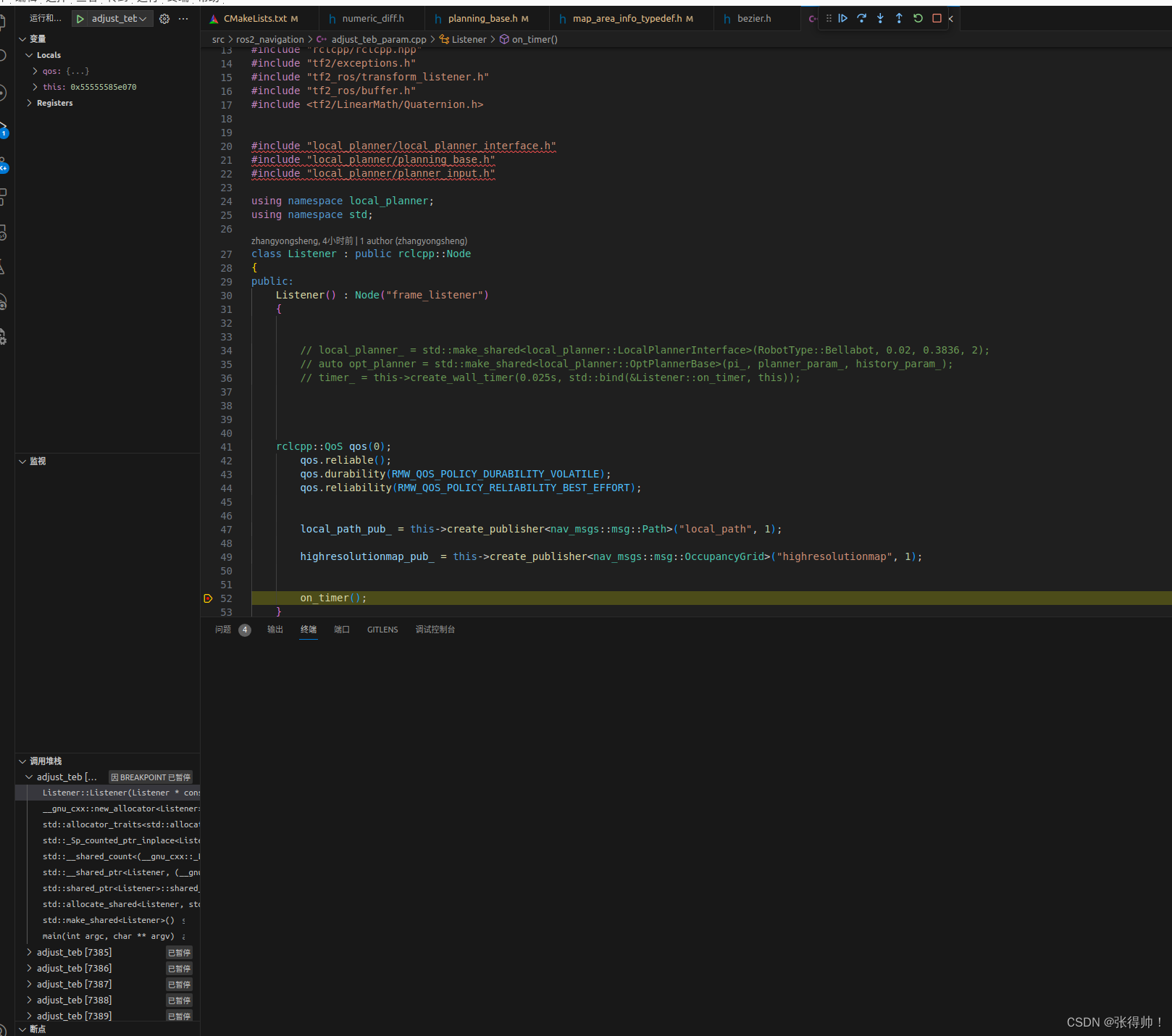
vscode 调试 ROS2
1、在下列目录同层级找到.vscode文件夹 . ├── build ├── install ├── log └── src 2、 安装ros插件 3、创建tasks.json文件,添加下列内容 //代替命令行进行编译 {"version": "2.0.0","tasks": [{"label": &…...

TuyaOS开发学习笔记(2)——NB-IoT开发SDK架构、运行流程
一、SDK架构 1.1 架构框图 基于 TuyaOS 系统,可以裁剪得到的适用于 NB-IoT 协议产品接入的 SDK。SDK 将设备配网、上下行数据通信、产测授权、固件 OTA 升级等接口进行封装,并提供相关函数。 1.2 目录结构 1.2.1 TuyaOS目录说明 adapter:T…...

Qt应用开发(基础篇)——普通按钮类 QPushButton QCommandLinkButton
一、前言 QPushButton类继承于QAbstractButton,是一个命令按钮的小部件。 按钮基类 QAbstractButton 按钮或者命令按钮是所有图形界面框架最常见的部件,当按下按钮的时候触发命令、执行某些操作或者回答一个问题,典型的按钮有OK,A…...
)
Data Structures Fan(cf)
考察异或运算以及前缀和 题意大概:给你一个长度为n的a数组,一个长度为n的01字符串,会询问q次 当x的值为1 给出 l r 将 l r 区间中的0 改变为1,1改变为0 。当x的值为2是 若随后的数为0 则输出当前字符串中 是0 的a数组中的数异或 …...
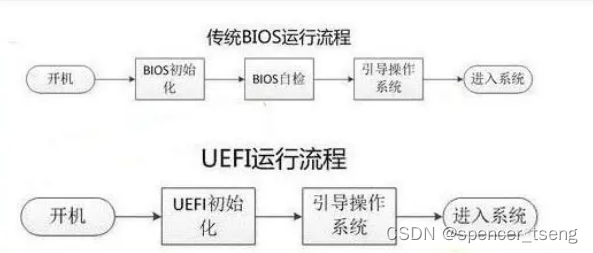
BIOS < UEFI
Basic Input Output System (BIOS) Unified Extensible Firmware Interface (UEFI)...
微信最新更新隐私策略(2023-08-15)
1、manifest.json 配置修改 在mp-weixin: 参数修改(没有就添加) "__usePrivacyCheck__": true, ***2、注意 微信开发者工具调整 不然一直报错 找不到 getPrivacySetting 废话不多说 上代码 3、 编辑首页 或者用户授权界面 <uni-popup…...

Java中xml转javaBean
Java中xml转javaBean maven坐标 <dependency><groupId>com.fasterxml.jackson.dataformat</groupId><artifactId>jackson-dataformat-xml</artifactId><version>2.13.4</version></dependency>代码测试 import cn.hutool.js…...

Spring Boot集成JPA和ClickHouse数据库
简介 Spring Boot是一个用于创建独立的、基于Spring的应用程序的框架。它具有快速开发特性,可以大大减少开发人员的工作量。JPA(Java Persistence API)是Java中处理关系型数据库持久化的标准规范,而ClickHouse是一个高性能、分布…...
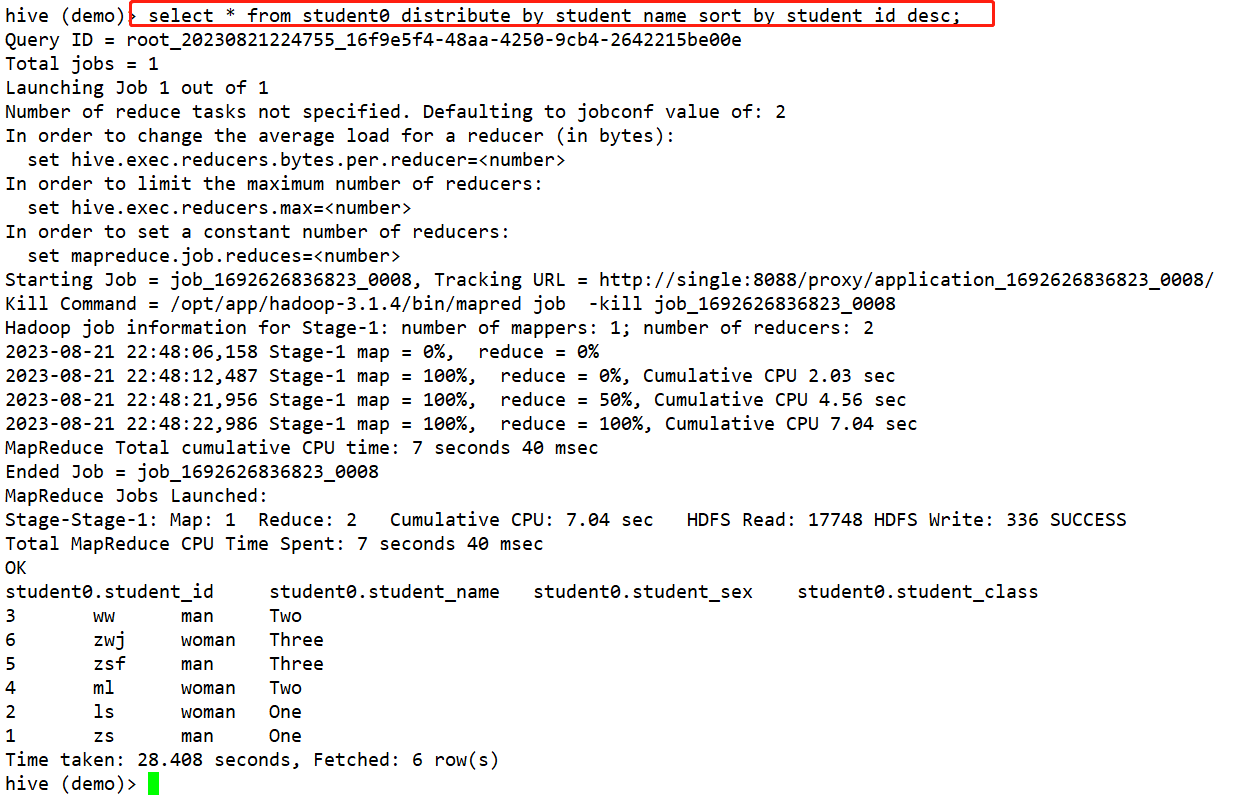
Hadoop生态圈中的Hive数据仓库技术
Hadoop生态圈中的Hive数据仓库技术 一、Hive数据仓库的基本概念二、Hive的架构组成三、Hive和数据库的区别四、Hive的安装部署五、Hive的基本使用六、Hive的元数据库的配置问题七、Hive的相关配置项八、Hive的基本使用方式1、Hive的命令行客户端的使用2、使用hiveserver2方法操…...
idea配置gitLab
前言:网上有很多类似的文章,但描述不够详细 步骤1:安装git 如果安装成功再次点击TEST按钮展示如下:git版本 步骤2:idea配置gitlab 查看当前项目管理的 远程仓库再git的地址,该地址可是gitLab的࿰…...
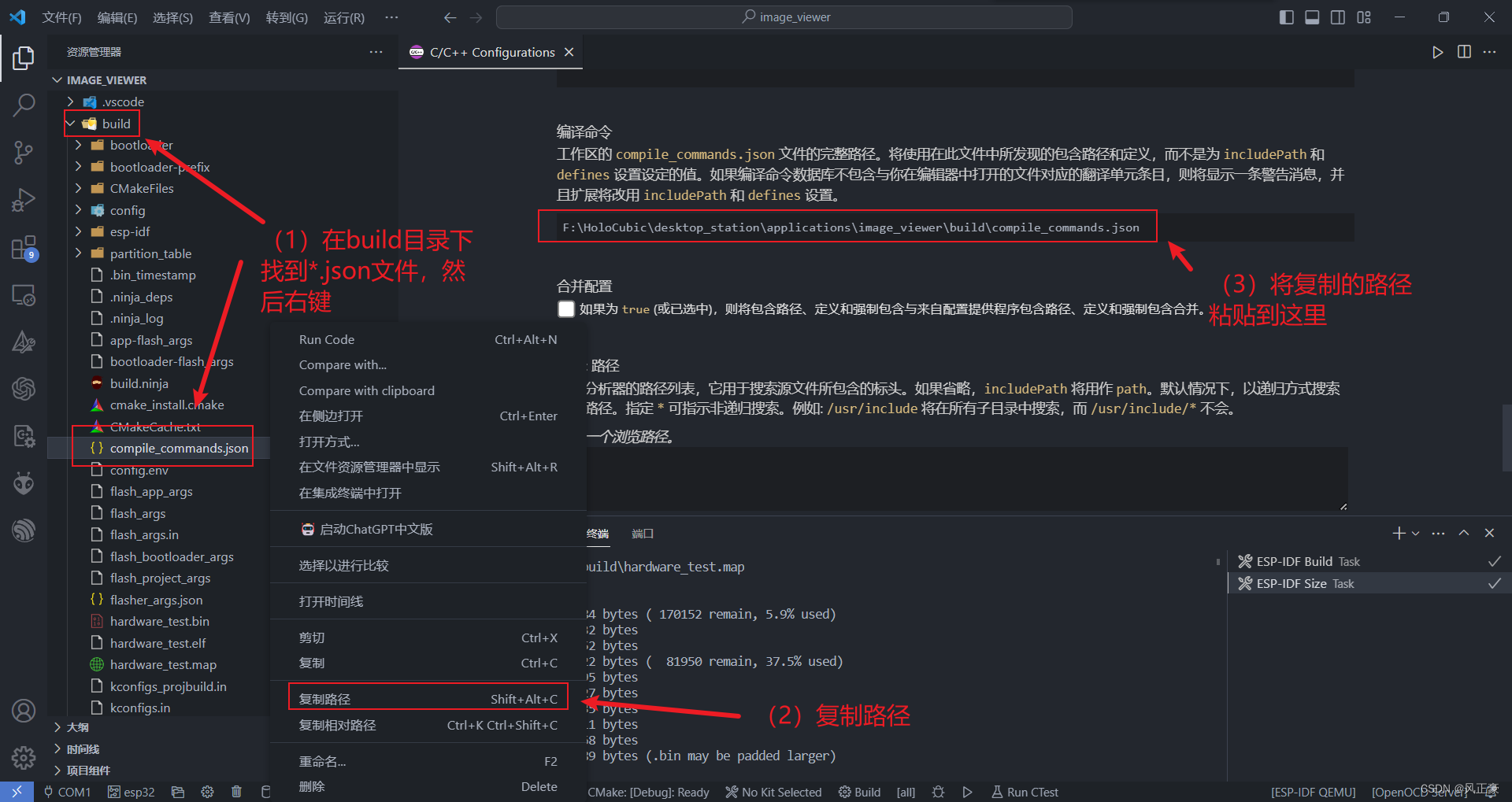
工程可以编译通过,但是Vscode依然有波浪线提示
前言 (1)我们在使用Vscode进行开发的时候,命名文件成功编译通过了,但是Vscode还是有波浪线的提示。 (2)其实成功编译通过就行,但是肯定还会存在一些强迫症患者,硬要消除这个报错。接…...
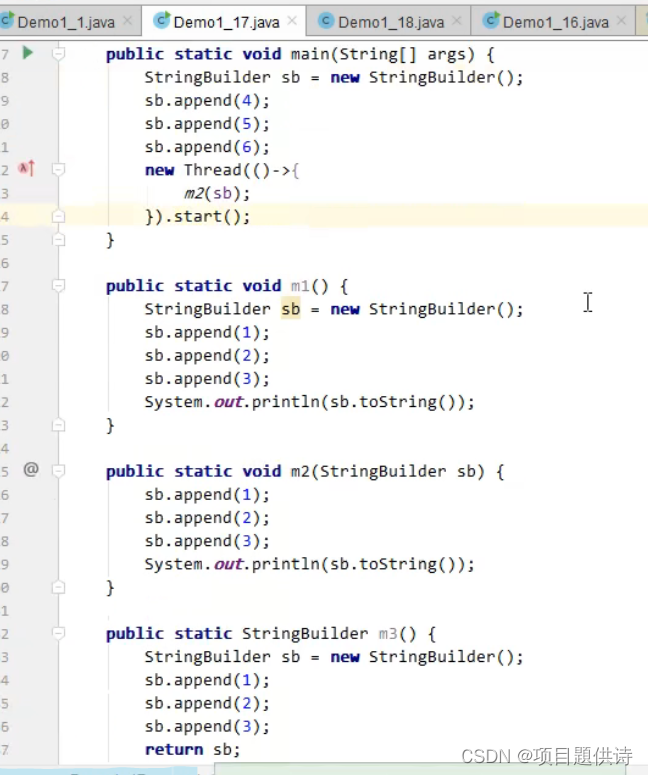
黑马JVM总结(二)
(1)栈 栈帧对应一次方法的调用,线程是要执行代码的,这些代码都是由一个个方法组成,线程运行的时候每个方法需要的内存叫做一个栈帧 (2)栈的演示 Frames:相当有栈 方法相当于栈帧…...

《Effective C++中文版,第三版》读书笔记7
条款41: 了解隐式接口和编译期多态 隐式接口: 仅仅由一组有效表达式构成,表达式自身可能看起来很复杂,但它们要求的约束条件一般而言相当直接而明确。 显式接口: 通常由函数的签名式(也就是函数名…...

脚本:python实现动态爱心
文章目录 效果代码Reference python实现dynamic heart 效果 代码 import turtle as tu import random as ratu.setup(0.5, 0.5) # 设置画板大小(小数表示比例,整数表示大小) tu.screensize(1.0, 1.0) # 设置屏幕大小 tu.bgcolor(black) #…...
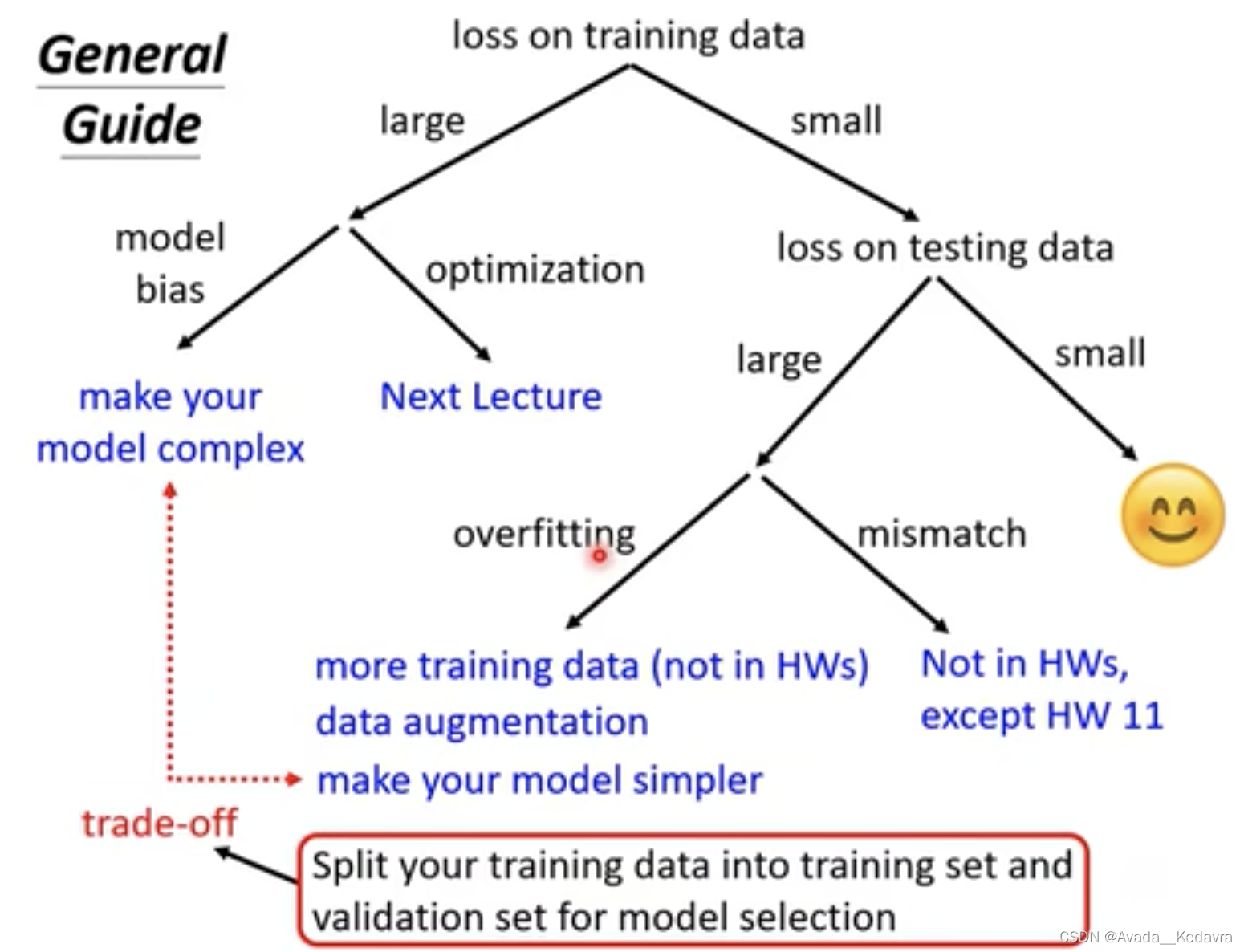
【李宏毅】深度学习6:机器学习任务攻略
如果在测试集上的效果不佳,应该要做什么?Optimization 如何选择?解决 overfitting 的方法? 测试集上的效果不佳 看训练数据的loss,是不是模型本身就没训练好? 问题:model 太简单了,…...
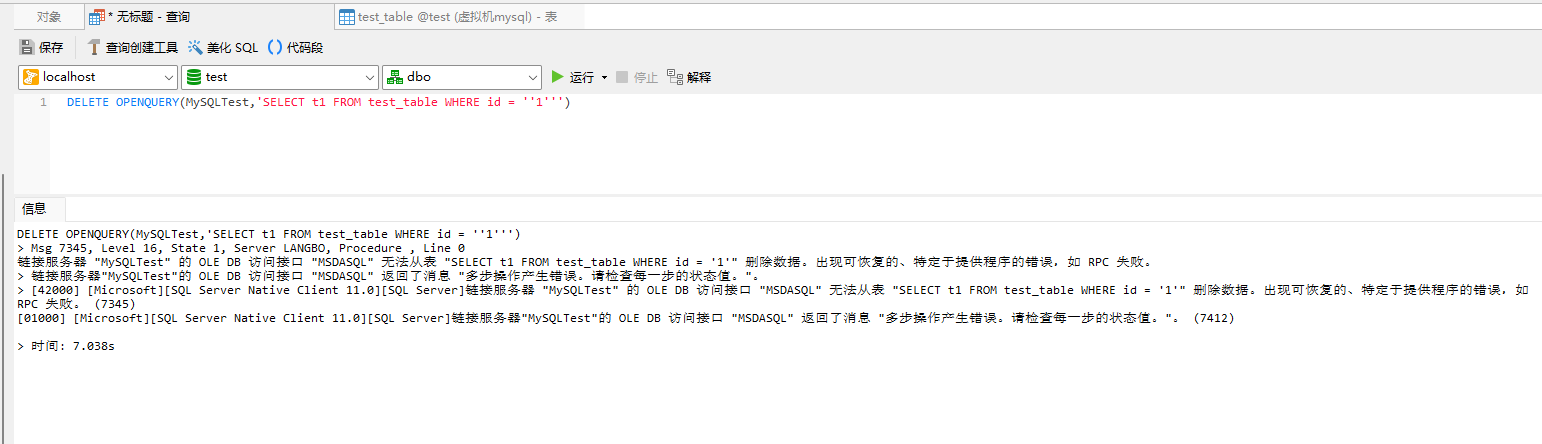
如何使用SQL SERVER的OpenQuery
如何使用SQL SERVER的OpenQuery 一、OpenQuery使用说明二、 OpenQuery语法2.1 参数说明2.2注解 三、示例3.1 执行 SELECT 传递查询3.2 执行 UPDATE 传递查询3.3 执行 INSERT传递查询3.4 执行 DELETE 传递查询 一、OpenQuery使用说明 在指定的链接服务器上执行指定的传递查询。 …...

element-tree树结构-默认选中第一个节点高亮-根据id选中节点高亮
前言 tree树结构是在开发中经常使用的组件,比如区域树,楼层树,组织架构树,等等包含节点关系 实际开发可能需要我们一进到页面选中树形结构第一个节点,并且调用数据,来达到用户体验 在用户选择之后&#x…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
