数学建模国赛C蔬菜类商品的自动定价与补货决策C
数学建模国赛C蔬菜类商品的自动定价与补货决策C
完整思路和代码请私信~~~
1.拟解决问题
这是一个关于生鲜商超蔬菜商品管理的复杂问题,需要综合考虑销售、补货、定价等多个方面。以下是对这些问题的总结:
问题 1: 蔬菜销售分析
需要分析蔬菜各品类和单品之间的销售量分布规律。
可以使用数据分析方法,如皮尔逊相关系数、多项式方程拟合等,来探讨销售之间的相关关系。
可以生成销售趋势图、相关性热图等可视化工具来展示关联关系。
问题 2: 品类补货与定价
需要分析不同蔬菜品类的销售总量与成本加成定价的关系。
可以构建定价模型,通常采用线性回归等方法,以最大化商超收益。
需要确定未来一周(2023 年 7 月 1-7 日)的日补货总量和定价策略,以最大化商超收益。
问题 3: 单品补货与定价
商超希望控制可售单品总数在 27-33 个,并满足最小陈列量的要求。
需要基于可售品种数据,制定单品补货计划和定价策略,同时满足市场需求并最大化收益。
可以采用线性规划等数学优化方法,以达到最优的补货和定价策略。
问题 4: 数据采集建议
采集蔬菜商品的历史销售数据,包括销售量、价格、销售时间等信息。
收集蔬菜的成本数据,包括采购价格、运输成本等。
获取市场需求数据,包括季节性需求波动、促销活动信息等。
收集蔬菜品相和运损率数据,以更好地理解蔬菜品质的影响。
考虑采集竞争商超的价格和销售数据,以进行市场竞争分析。
2.问题1
数据清洗
删除重复值:使用唯一标识符如单品编码,删除附件1和附件2中的重复数据,确保每个单品仅出现一次。
缺失值处理:检查是否存在缺失值,可以选择删除包含缺失值的行或填充缺失值,以确保数据完整性。
异常值处理:检测销售价格的异常值,特别关注价格未变动但商品未出售的情况,采用统计或可视化方法来处理异常值。
数据合并:使用VLOOKUP等方法将附件1和附件2中的数据合并,以便后续分析和建模。
销量分析:
以不同时间维度进行销量分析,包括小时、天、月等:
以小时为单位: 统计某一天内每个小时的销量变化,创建频率分布直方图,例如,确定菠菜在哪个小时销量最高。也可以对单个蔬菜品类进行统计,比如金针菇的平均、最大和最小销量。
以天为单位: 对24小时数据进行汇总,分析从2020年6月到2023年6月的销售趋势。使用FFT等方法检测数据的周期性,然后使用非线性函数进行拟合,如ARIMA或指数函数,以了解销售趋势。
以月为单位: 对30天数据进行汇总,分析36个月的销售趋势。考虑整体类别的变化趋势,如花叶类、食用菌、辣椒类等,可以使用线性回归等方法来分析趋势。
其他时间维度: 还可以考虑季度等其他时间维度,根据题目提供的信息,分析蔬菜供应的季节性变化对销售组合的影响。
参考一
import numpy as np
import matplotlib.pyplot as plt# 加载数据,这里假设数据已经在alldata.mat中
# 假设alldata.mat中包含了pinglei和xiaoliang的数据# 对应MATLAB的for循环,计算yuepinglei和yuexiaoliang
yuepinglei = np.zeros((number_of_rows, 36))
yuexiaoliang = np.zeros((number_of_rows, 36))for i in range(36):yuepinglei[:, i] = np.sum(pinglei[:, i*30:(i+1)*30], axis=1)yuexiaoliang[:, i] = np.sum(xiaoliang[:, i*30:(i+1)*30], axis=1)# 对应MATLAB的plot命令
plt.plot(np.arange(1, 37), yuepinglei)
shuju = np.column_stack((yuepinglei[1, :], yuexiaoliang[100:105, :]))# 接下来是数据处理和计算gamma的部分,注意这部分代码在MATLAB和Python之间存在一些差异,
# 具体实现可能需要根据数据的结构进行适当的修改。
# 请根据您的数据和需求进一步自定义Python代码。参考二:
load("alldata.mat");% 将pinglei和xiaoliang按月份汇总
yuepinglei = reshape(sum(reshape(pinglei, [], 30), 2), [], 36);
yuexiaoliang = reshape(sum(reshape(xiaoliang, [], 30), 2), [], 36);% 提取数据并进行标准化
shuju = [yuepinglei(2, :)', yuexiaoliang(101:105, :)'];
avg = mean(shuju);
biaozhunhua = shuju ./ avg;% 计算灰色关联系数
Y = biaozhunhua(:, 1);
X = biaozhunhua(:, 2:end);
a = min(min(abs(X - Y)));
b = max(max(abs(X - Y)));
ro = 0.5;
gamma = (a + ro * b) ./ (abs(X - Y) + ro * b);% 打印关联系数并排序
disp("子序列中各个指标的灰色关联度分别为:");
ans = mean(gamma);
[ans1, ind] = sort(ans, 'descend');% 绘制灰色关联分析的折线图
figure(1)
t = 1:36;
color = ["b", "r", "g", "b", "r"];
for i = 1:5plot(t, gamma(:, i), color(i) + '*--')hold on
end
xlabel('year')
legend('青梗散花', '西兰花', '枝江青梗散花', '紫白菜(1)', '紫白菜(2)')
title('灰色关联分析')3.问题二
Step 1: 数据预测
首先,需要利用历史销售数据来预测未来一周内每个蔬菜品类的每天销售量。这可以通过多种方法实现,包括灰色预测、时间序列分析、回归分析、机器学习等。这个预测过程将产生关于销售量、成本和定价的基本数据,以便后续优化。
Step 2: 关联分析
接下来,需要分析销售量、成本和定价之间的关联关系。这可以包括机理分析,即为什么某些商品在某些条件下销售得更好。这个步骤有助于理解变量之间的相互影响。
Step 3: 建立规划模型
在此步骤中,需要建立一个规划模型,以最大化商超的利润收益为目标。决策变量通常包括补货总量和定价策略。模型的目标是找到最佳的补货策略和定价策略,以实现最大利润。
在建立模型时,需考虑以下约束条件:
每天的总补货量不能超过商超的库存容量。
每个蔬菜品类的销售总量受到限制。
考虑损耗率,确保不会采购过多导致浪费。
考虑退货情况,以避免不必要的成本。
Step 4: 求解优化方案
最后,使用适当的优化算法来解决建立的规划模型,以获得对应的优化方案。由于数据量可能较大,可以考虑使用遗传算法、模拟退火算法、粒子群算法等。也可以尝试暴力搜索算法或网格搜索算法,根据问题的复杂性选择合适的方法。
4.问题三
单品类别预测: 对每个小品类进行单独的销售量预测,使用历史销售数据和适当的预测方法,例如时间序列分析、回归分析、机器学习等。预测未来一周内每个小品类每天的销售量。
优化模型建立: 基于销售量预测,建立优化模型,目标是最大化利润收益。决策变量包括27-33个小品类的补货总量和定价策略。考虑成本、销售额、库存等因素。
约束条件:
确保每个小品类的订购量满足最小陈列量要求,通常为2.5千克。
控制售卖的小品类总数在27-33个之间,以满足商超的要求。
考虑市场对各品类蔬菜商品的供需关系,以确保销售量和定价策略满足市场需求。
确保成本、销售额、库存等因素在合理范围内。
求解方法: 使用优化算法如遗传算法、模拟退火算法、粒子群算法等,对建立的优化模型进行求解,以获得最佳的补货总量和定价策略。
5.问题四
6.更多细节和代码(欢迎私信)
详细代码资料:https://github.com/HuaandQi/Mathematical-modeling.git
相关文章:

数学建模国赛C蔬菜类商品的自动定价与补货决策C
数学建模国赛C蔬菜类商品的自动定价与补货决策C 完整思路和代码请私信~~~ 1.拟解决问题 这是一个关于生鲜商超蔬菜商品管理的复杂问题,需要综合考虑销售、补货、定价等多个方面。以下是对这些问题的总结: 问题 1: 蔬菜销售分析 需要分析蔬菜各品类和…...
的重要性)
在程序开发中,接口(interface)的重要性
开了很多人写的程序,都适用了接口,也适用了注入,也没有感到什么不妥。如果只是为了注入而写接口,其实我感觉大可不必,特别是把接口和实体写在一个项目项目中的。 我不知道其他人怎么看接口这一层,接口最大的…...

MyBatis关联关系映射详解
前言 在使用MyBatis进行数据库操作时,关联关系映射是一个非常重要的概念。它允许我们在数据库表之间建立关联,并通过对象之间的关系来进行数据查询和操作。本文将详细介绍MyBatis中的关联关系映射,包括一对一、一对多和多对多关系的处理方法…...
常用电子元器件基础知识
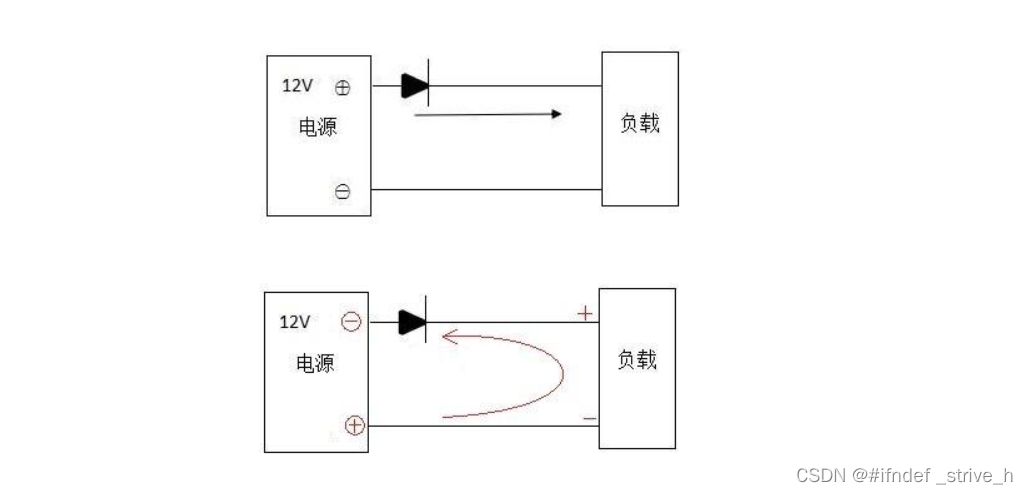
目录 一、电阻 二、电容 三、电感 四、保险丝 五、二极管 一、电阻 概念:顾名思义,就是增加电流通过的阻力的。 就像是在水渠中放入东西,能阻止水的顺利通过也是一个道理。 基于电阻的电气特性,电阻在电路中主要有以下四个…...
git撤销还未push的的提交
怎样撤销掉上图中的提交呢 使用以下代码即可提交 git reset --soft HEAD^...

MySQL--数据库基础
数据库分类 数据库大体可以分为 关系型数据库 和 非关系型数据库 常用数据类型 数值类型: 分为整型和浮点型: 字符串类型 日期类型...
Excel相关笔记
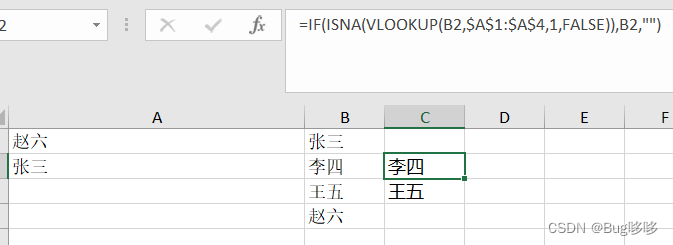
1、找出B列中A列没有的数据并放在C列 公式:IF(ISNA(VLOOKUP(B1,$A 1 : 1: 1:A$4,1,FALSE)),B1,“”)...
RouterOS-配置PPPoEv4v6 Server
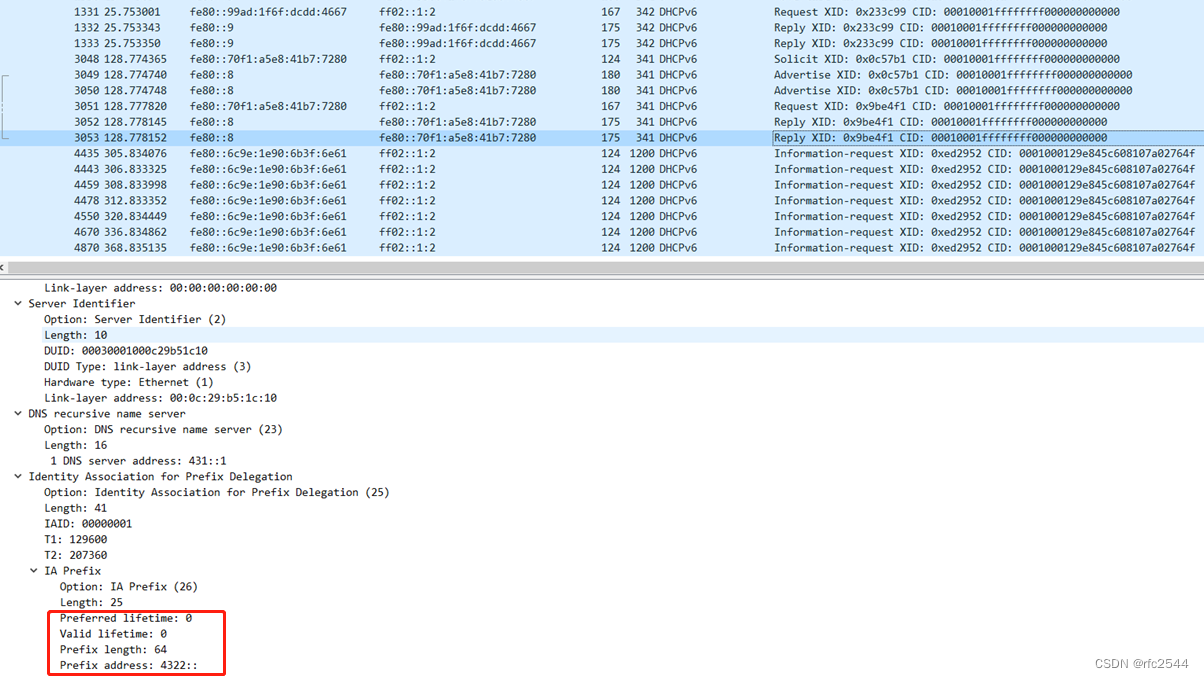
1 接口 ether3 出接口 ether4 内网接口 2 出接口 出接口采用PPPoE拨号SLAAC获取前缀,手动配置后缀 2.1 选择出接口interface,配置PPPoE client模式 2.2 配置PPPoE client用户名和密码 2.3 从PPPoE client获取前缀地址池 2.4 给出接口选择前缀并配置…...

PhpStorm软件安装包分享(附安装教程)
目录 一、软件简介 二、软件下载 一、软件简介 PhpStorm是一款由JetBrains开发的专业PHP集成开发环境(IDE),旨在提供全面的PHP开发支持。它是基于IntelliJ IDEA平台构建的,具有强大的功能和工具,可以帮助开发人员提高…...

JavaScript设计模式(三)——单例模式、装饰器模式、适配器模式
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...

LeetCode:有序数组的平方
题目 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 示例 1: 输入:nums [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变…...

数学分析:势场
首先从散度的物理解释开始。首先,在球内的向量场的散度的积分,等于它在球边界上的流量的积分。所以根据积分中值定理,我们可以这么理解散度,它就是这个体积内的速度场的平均密度。而速度场只和源有关,所以它表示的某个…...

MySQL 中 MyISAM 与 InnoDB 引擎的区别
分析&回答 区别很多,大家说出下面几点,面试就应该 OK 了 1) 事务支持 MyISAM不支持事务,而InnoDB支持。InnoDB的AUTOCOMMIT默认是打开的,即每条SQL语句会默认被封装成一个事务,自动提交,这样会影响速…...
【javascript】禁止浏览器调试前端页面
目录 为啥要禁止?无限 debugger基础禁止调试解决对策 为啥要禁止? 由于前端页面会调用很多接口,有些接口会被别人爬虫分析,破解后获取数据,为了杜绝这种情况,最简单的方法就是禁止人家调试自己的前端代码 …...
 的过程)
Oracle Non-CDB配置 TDE(透明数据加密) 的过程
说明 此文档虽然是针对non CDB而写,但是对于CDB的操作过程也是类似的,即在CDB$ROOT中设置完成wallet设置后,在PDB中设置和打开MEK即可。 先决条件 请确保目录$ORACLE_SID/admin/$ORACLE_SID存在,例如此目录为: /u01/app/oracl…...

MySQL——常见问题
NULL和空值的区别 1、空值不占空间,NULL值占空间。当字段不为NULL时,也可以插入空值。 2、当使用 IS NOT NULL 或者 IS NULL 时,只能查出字段中没有不为NULL的或者为 NULL 的,不能查出空值。 3、判断NULL 用IS NULL 或者 is no…...
在FPGA上快速搭建以太网
在本文中,我们将介绍如何在FPGA上快速搭建以太网 (LWIP )。为此,我们将使用 MicroBlaze 作为主 CPU 运行其应用程序。 LWIP 是使用裸机设计以太网的良好起点,在此基础上我们可以轻松调整软件应用程序以提供更详细的应用…...

如何防范 AI 盗取你的密码
现如今,随着人工智能(AI)应用的普及和快速迭代,几乎任何人都可以轻而易举地利用AI进行密码破解之类的攻击。这已经引起了业界的担忧。下面,我将围绕着:密码破解究竟意味着什么,基于AI的密码猜测…...

华清远见第六课程作业day3
类 栈 #include <iostream>using namespace std;class Sta{ private:int *data;int top; public:Sta():data(new int(128)){top-1;cout<<"stack::无参构造:"<<endl;}~Sta(){delete data;cout<<"stack::析构函数:"<<this<…...

Rabbitmq配置定义
RabbitMQ 环境变量 RabbitMQ 的环境变量都是以"RABBITMQ_"开头的,可以在Shell 环境中设置,也可以在配置文件中定义。默认的配置文件如下: ## /etc/rabbitmq/rabbitmq-env.conf 定义配置文件: /va/lib/rabbitmq/ 的目…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
