「程序员必须掌握的算法」动态规划「上篇」
动态规划详解
动态规划 (Dynamic Programming) 是一种算法思想,用于解决一些复杂的问题。本文将介绍动态规划的分类、概念和经典例题讲解。
动态规划的分类
动态规划可以分为以下两种类型:
- 0/1背包问题:该问题是动态规划的一种基本类型。在背包问题中,有n个物品可以放入容量为W的背包中,每个物品有自己的重量和价值。需要选择哪些物品能够最大化背包的总价值。
- 最长公共子序列问题:该问题是另一种经典的动态规划类型,涉及到两个字符串,并找到这两个字符串之间的最长公共子序列。
动态规划的概念
在解决动态规划问题时,我们需要定义以下概念:
- 状态 (State):问题中需要优化的变量,如背包问题中的容量,最长公共子序列问题中的字符串长度等。
- 状态转移方程 (State Transition Equation):描述状态之间的转移过程,即问题的递推关系。例如,在背包问题中,每个物品可以放入背包或不放入背包。因此,状态转移方程可以表示为: d p [ i ] [ j ] = max ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w i ] + v i ) dp[i][j] = \max(dp[i-1][j], dp[i-1][j-w_i]+v_i) dp[i][j]=max(dp[i−1][j],dp[i−1][j−wi]+vi) 其中dp[i][j]表示在使用前i个物品时,填满j容量的背包的最大价值。
- 初始状态 (Initial State):问题的初始条件,通常为问题规模最小的情况下的答案。在背包问题中,初始状态为dp[0][0]=0。
- 边界状态 (Boundary State):问题的边界条件,在状态转移过程中需要特别处理的状态。在背包问题中,背包的容量不能为负数,因此需要在状态转移方程中特别处理。
经典例题讲解
下面我们将分别介绍0/1背包问题和最长公共子序列问题的解法。
1. 0/1背包问题
题目描述:有n个物品和一个容量为W的背包。第i个物品的重量为wi,价值为vi。现在,需要选择一些物品放入背包,使得放入的物品的总重量不超过W,且总价值最大。求最大价值。
解题思路:定义状态dp[i][j]为在使用前i个物品时,填满j容量的背包的最大价值。状态转移方程如下所示: d p [ i ] [ j ] = { d p [ i − 1 ] [ j ] , j < w i max ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − w i ] + v i ) , j ≥ w i dp[i][j] = \begin{cases}dp[i-1][j],&j<w_i\\ \max(dp[i-1][j], dp[i-1][j-w_i]+v_i),&j\ge w_i\end{cases} dp[i][j]={dp[i−1][j],max(dp[i−1][j],dp[i−1][j−wi]+vi),j<wij≥wi 其中dp[i-1][j]表示不放入第i个物品的最大价值,dp[i-1][j-w[i]]+v[i]表示将第i个物品加入背包的最大价值。需要注意的是,如果当前背包容量小于物品的重量,就不能将该物品放入背包。因此,需要特别处理背包容量小于物品重量的情况。
代码实现:
int dp[101][1001];
int weight[101], value[101];int knapSack(int n, int w)
{memset(dp, 0, sizeof(dp));for (int i = 1; i <= n; i++) {for (int j = 1; j <= w; j++) {if (j < weight[i]) {dp[i][j] = dp[i-1][j];} else {dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);}}}return dp[n][w];
}
2. 最长公共子序列问题
题目描述:给定两个字符串A和B,找到它们的最长公共子序列 (LCS)。
解题思路:定义状态dp[i][j]为字符串A的前i个字符和字符串B的前j个字符的LCS长度。状态转移方程如下所示:
d p [ i ] [ j ] = { 0 , i = 0 或 j = 0 d p [ i − 1 ] [ j − 1 ] + 1 , A i = B j max ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) , A i ≠ B j dp[i][j] = \begin{cases}0,&i=0\text{或}j=0\\ dp[i-1][j-1]+1,&A_i=B_j\\ \max(dp[i-1][j], dp[i][j-1]),&A_i\neq B_j\end{cases} dp[i][j]=⎩ ⎨ ⎧0,dp[i−1][j−1]+1,max(dp[i−1][j],dp[i][j−1]),i=0或j=0Ai=BjAi=Bj
当A[i-1]等于B[j-1]时,dp[i][j]等于dp[i-1][j-1]+1,表示A和B中的相同字符加上它们前面的LCS。当它们不相等时,LCS为它们前面的LCS的最大值,即dp[i-1][j]和dp[i][j-1]的最大值。
代码实现:
int dp[1001][1001];
string A, B;int LCS(int n, int m)
{for (int i = 0; i <= n; i++) {for (int j = 0; j <= m; j++) {if (i == 0 || j == 0) {dp[i][j] = 0;} else if (A[i-1] == B[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;} else {dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}}}return dp[n][m];
}
结语
动态规划是一种非常重要的算法思想,它通常用于解决复杂的问题。在应用动态规划解决问题时,需要注意定义状态、状态转移方程、初始状态和边界状态等概念。对于不同类型的动态规划问题,需要采用不同的解决方法。希望本文能够帮助读者加深对动态规划的理解。
相关文章:

「程序员必须掌握的算法」动态规划「上篇」
动态规划详解 动态规划 (Dynamic Programming) 是一种算法思想,用于解决一些复杂的问题。本文将介绍动态规划的分类、概念和经典例题讲解。 动态规划的分类 动态规划可以分为以下两种类型: 0/1背包问题:该问题是动态规划的一种基本类型。…...

什么是Linux
什么是Linux? 不知道大家是什么时候开始接触Linux,我记得我是大三的时候,那时候通过国嵌、韦东山的教学视频,跟着搭bootloader,修改内核,制作根文件系统,一步步,视频真的很简单&…...
学习笔记|定时器|STC中断|定时器时间计算|STC32G单片机视频开发教程(冲哥)|第十一集:定时器的作用和意义
文章目录 1.定时器的作用和意义定时器中断定时器是定时器和计数器的统称。 2.STC32G单片机定时器使用原理2.1 先设置功能为定时器/计数器(本质都是加法计数器)2.2、在定时器模式下,设置不分频或者12分频∶Tips:选择不分频还是12分频2.3、定时器的工作模式…...

第28节-PhotoShop基础课程-图层操作
文章目录 前言1.像素图层2.删除 Delete3.合并 Ctrl E4.盖印 Ctrl Shift Alt5.图层顺序-拖动就可以6.编组-Ctrl G 管理图层-分类存放7.锁定图层-背景图层8.不透明度9.查找图层 2.智能图层1.能保持图片放大缩小(Ctrl T)的时候不丢失分辨率2.和滤镜配合使…...
)
CGAL 闵可夫斯基和(Minkowski Sums)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 假设给定两个集合 A , B ∈ R d A,B∈R^d A,B...

Layui快速入门之第二节布局容器(固定宽度与完整宽度)
目录 一:固定宽度 二: 完整宽度 一:固定宽度 将栅格放入一个带有 class"layui-container" 的特定容器中,以便在小屏幕以上的设备中固定宽度,让列可控(两侧有留白效果) <!--固定宽度(两侧有留白效果)--&…...

异地容灾系统和数据仓库中数据同步的设计软件的功能模型
( 1)初始同步模块 该模块主要是在表进行初始同步时使用的;它能够根据实际需要生成物化视图 及其索引的创建语句,并完成表的初始同步。如果没有特别的要求,则调用普通初 始同步子模块进行目的端表的初始同步ÿ…...

分布式调度 Elastic-job
分布式调度 Elastic-job 1.概述 1.1什么是任务调度 我们可以思考一下下面业务场景的解决方案: 某电商平台需要每天上午10点,下午3点,晚上8点发放一批优惠券某银行系统需要在信用卡到期还款日的前三天进行短信提醒某财务系统需要在每天凌晨0:10分结算…...

第 2 章 线性表(学生健康登记表实现)
1. 示例代码 1) status.h /* DataStructure 预定义常量和类型头文件 */#ifndef STATUS_H #define STATUS_H/* 函数结果状态码 */ #define TRUE 1 /* 返回值为真 */ #define FALSE 0 /* 返回值为假 */ #define RET_OK 0 /* 返回值正确 */ #define INFEASI…...
)
第三周晨考自测(3.0)
1.获取元素的偏移量 offsetLeft和offsetTop 分别获取的是元素元素左边的偏移量和上边的偏移量 语法:元素对象.offsetLeft /元素对象.offsetTop 返回值:就是该元素对应的偏移量,是一个具体的数字 offsetLeft:该元素相对于参考…...

C++ 结构体
前文 C中的结构体是一种非常有用的数据类型,它允许我们将不同的变量组合在一起,形成一个自定义的数据结构。 结构体在C中的应用非常广泛,它可以用来表示和管理各种实体、对象或数据的属性。比如,在一个学生管理系统中,…...
如何使用聊天GPT自定义说明
推荐:使用 NSDT场景编辑器 快速搭建3D应用场景 OpenAI ChatGPT正在席卷全球。一周又一周,更新不断提高您可以使用这种最先进的语言模型做什么的标准。 在这里,我们深入研究了OpenAI最近在ChatGPT自定义指令上发布的公告。此功能最初以测试版…...
mac pyenv无法切换python版本问题
看是zsh还是bash echo $SHELLzsh 配置到~/.zshrc 文件 vim ~/.zshrcexport PYENV_ROOT"$HOME/.pyenv" command -v pyenv >/dev/null || export PATH"$PYENV_ROOT/bin:$PATH" 执行 source ~/.zshrc bash vim ~/.bashrc export PYENV_R…...

API接口接入电商平台案例,采集淘宝天猫拼多多1688京东LAZADA数据按关键字搜索商品示例
按关键字搜索商品数据API接口可以让用户轻松地在海量商品中找到自己需要的商品。这个接口包括多种搜索方式,例如利用关键字搜索商品名称、商品描述、商品分类、商家信息等。同时,还可以通过不同的排序方式进行筛选,例如销量排行、价格排行、评…...
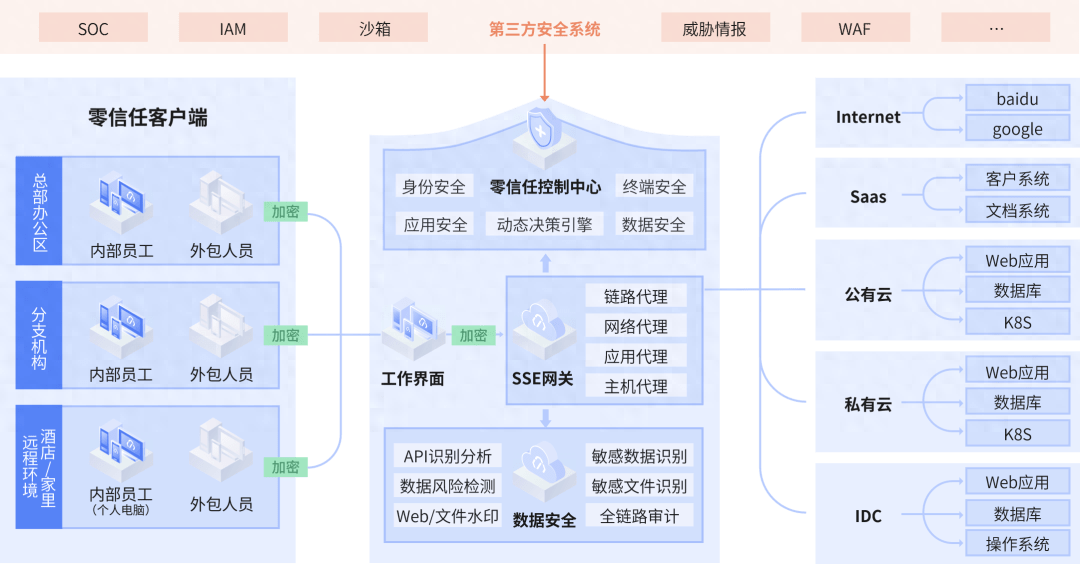
持安-大连万达集团零信任项目入选中国信通院2023零信任优秀案例
2023年8月25日,以“链接云端,可信而安”为主题的“2023首届SecGo云和软件安全大会”在京隆重召开。会上,中国信息通信研究院重磅揭晓了“安全守卫者计划”优秀案例评选结果。 零信任办公安全技术创新企业持安科技,与用户大连万达…...

python28种极坐标绘图函数总结
文章目录 基础图误差线等高线polar场图polar统计图非结构坐标图 📊python35种绘图函数总结,3D、统计、流场,实用性拉满 matplotlib中的画图函数,大部分情况下只要声明坐标映射是polar,就都可以画出对应的极坐标图。但…...

C#编程基础(万字详解,这一篇就够了)
C#及其开发环境简介 C#概述 C#的编程功能 C#与.Net的关系 .Net C# C#的集成开发环境 Windows上编写C#程序 Linux/Mac OS上编写C#程序 运行第一个HelloWorld程序 C#基本语法 程序实例 C#基本语法 using关键字 class关键字 注释 成员变量 成员函数 实例化一个类…...

SpringBoot中自定义注解
目录 SpringBoot中自定义注解 关于注解的解释 元注解 Documented Target Retention Inherited Native 自定义注解 自定义注解与SpringBoot全局异常处理完成参数校验 约束验证器 自定义全局异常处理器 自定义注解完成数据脱敏 定义脱敏策略枚举 自定义注解 实行脱…...

《TCP/IP网络编程》阅读笔记--地址族和数据序列
目录 1--IP地址和端口号 2--地址信息的表示 3--网络字节序与地址变换 4--网络地址的初始化与分配 5--Windows部分代码案例 1--IP地址和端口号 IP 地址分为两类: ① IPv4 表示 4 字节地址族; ② IPv6 表示 16 字节地址族; IPv4 标准的 4 …...

【C++】可变参数模板
2023年9月9日,周六下午 这个还是挺难学的,我学了好几天... 在这里我会举大量的示例程序,这样可以有一个更好的理解, 不定期更新。 目录 推荐文章: 示例程序一:拼接字符串 示例程序二:求整…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
