数据结构——复杂度讲解(2)
作者:几冬雪来
时间:2023年2月22日
内容:数据结构复杂度讲解
目录
前言:
复杂度讲解(2):
1.空间复杂度是什么:
2.空间复杂度讲解:
结尾:
前言:
在这之前我们写了一篇博客,内容是对我们的数据结构的复杂度进行了一个初步的讲解,并通过了几道题对我们的知识进行了巩固。但是我们的数据结构的复杂度讲解并没有就此结束,今天我们将对我们的数据结构的复杂度进行进一步的分析说明。

复杂度讲解(2):
在我们上一篇的数据结构的讲解中,我们对我们复杂度中的时间复杂度进行了一个大致的说明,但是我们也说过,我们的时间复杂度只是我们算法效率的其中一个复杂度,因此今天我们将对另一个复杂度——空间复杂度进行讲解。
1.空间复杂度是什么:
在上一篇博客我们讲到,要衡量我们算法的效率可以从时间和空间两个维度进行讲解,时间复杂度是我们的代码大概运行的次数,那么我们的另一个维度,空间复杂度是什么呢?在我们的数据结构中,我们的空间复杂度也是一个数学表达式。它是对一个算法在运行过程中临时占用存储空间大小的量度。
它在这里并不是计算我们的字节大小,而是计算变量的个数。 其次我们的空间复杂度的计算也是使用我们的大O的渐进表示法。它和我们时间复杂度的计算原理十分相似。
2.空间复杂度讲解:
我们依旧写题进行举例,来计算我们的空间复杂度。就例如我们下面这个冒泡排序的空间复杂度的计算。

但是对于我们这个代码的空间复杂度出现了两种不一样的看法。
有点人认为我们这里创造了3个临时变量,有人则认为我们这里的临时变量要更多,那是为什么呢? 首先是我们的最明显的三个临时变量,这个大家应该都是没有争议的。
到这里有人就下结论了,我们这里的变量的个数是一个常数,因此我们这里的空间复杂度应该被写为O(1)。但是有人就有不一样的看法,有人就看到了我们这个代码的参数,我们这里使用传址调用传递了我们一个数组的地址,而我们的数组中有n个值,所以我们这里的空间复杂度应该是O(N)。
那么这里就引申了一个问题,在我们的这个冒泡排序中,到底有没有计算我们这个数组的空间?
这里就要结合我们上面的定义,这里我们的数组并不是为了计算我们的数组所创建的,它是我们数据源的提供。因为我们要对我们的数组进行冒泡排序,所以我们才引进了这一个数组,所以我们这里数组的个数并未算入其中,所以我们这里就只创造了三个临时变量,我们的空间复杂度为O(1)。
那么搞懂了这道题之后,接下来我们再写一道题。

这是我们的斐波那契函数,不同的是,这里我们并不是计算我们数组第n项的值,而是计算我们的前n项。 所以这里我们通过我们的malloc函数开辟了一块n+1大小的空间,而且这里我们的这块数组和我们的冒泡排序的题不一样,这里是为了计算我们的斐波那契前n项所额外开辟的一个数组,因此我们这个代码的空间复杂度是O(N)。
通过这两个代码,其实我们可以看出我们的空间复杂度并没有时间复杂度那么复杂。

接下来我们再做几道题目来巩固一下知识。
在上面上面求出了冒泡排序和斐波那契函数的空间复杂度,那么接下来我们就再来求一求我们递归函数的空间复杂度。

这里我们如果简单来看,我们这个函数并没有建立什么临时变量,因此我们的空间复杂度是O(1)。 但是其实这里我们运用到了递归的知识,而递归则要建立栈帧。而在这里,我们要建立N+1层栈帧。

这里我们就累计创建了N+1层栈帧,所以我们的空间复杂度是O(N)。这是为了运行我们的算法所而外开辟的空间。
下来我们再看一道题。

这道题我们之前讲过它的时间复杂度,我们这个代码的时间复杂度是O(2^N)。 你瞒我瞒这个代码的空间复杂度也是O(2^N)吗?其实不是,我们这个代码的空间复杂度其实是O(N)。为什么?这里就涉及一个问题,递归调用是怎么样调用的?

这里我们斐波那契函数从N开始,一开始我们调用的是N-1,接下来我们并不是调用同一行的N-2,我们是会继续往下执行,调用我们下方的N-2。 当我们最左边的斐波那契函数调用到不能再调用的时候我们就往回返回,接下来我们才继续往右边继续调用。
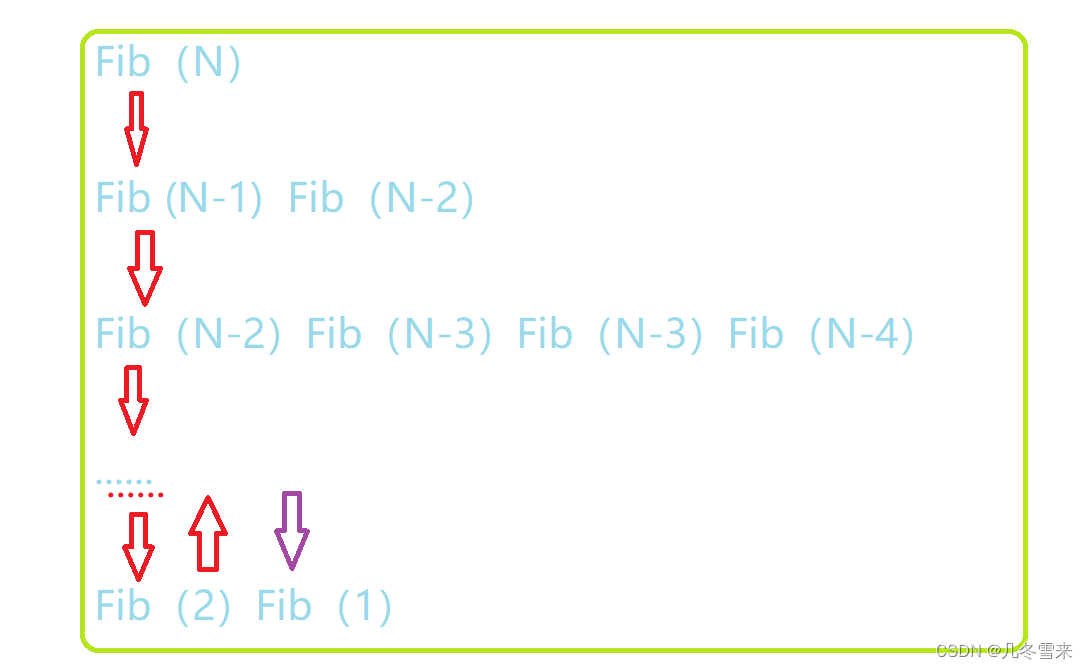
而且在这里我们的第一次调用结束的Fib(2)和我们返回后再次向下调用的Fib(1)是同一块空间。
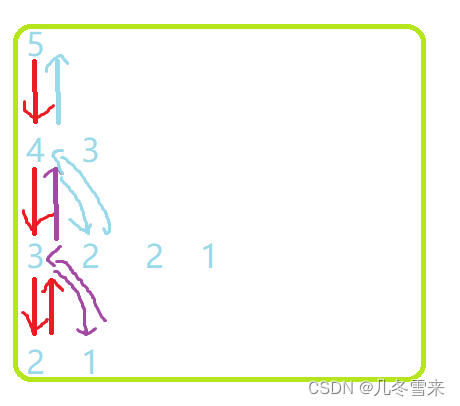
这里就是我们的大概的运行过程。这里我们通过对比时间复杂度和空间复杂度也可以知道一个道理。
时间一去不复返,不可以重复利用
空间用了之后归还,可以重复利用
到这里,除了一部分比较复杂的空间复杂度,我们的空间复杂度到这里就基本讲解完了。通过以上用例,我们可以看出对比起我们的时间维度,我们的空间维度的例题讲解就相对较少。但是从我们后面的两道题目的讲解来看,我们算法效率的空间复杂度并不是那么简单的。最后一题如果没有进行讲解的话,可能大部分人都会掉到坑里,大多数人以为空间销毁就是指这块空间消失了,其实我们空间的销毁实际上可以理解为是将我们这块空间的使用权还给我们的操作系统。
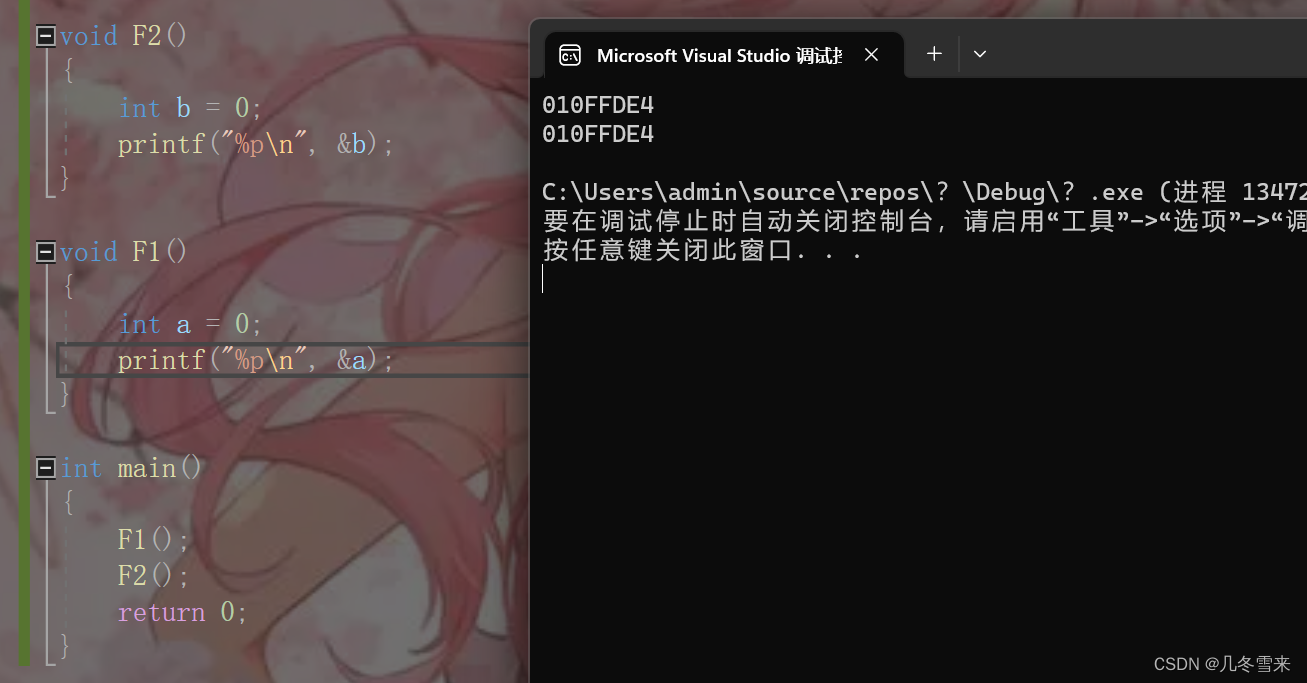
类似我们的这个代码,就能大概解释我们上面的两道题。
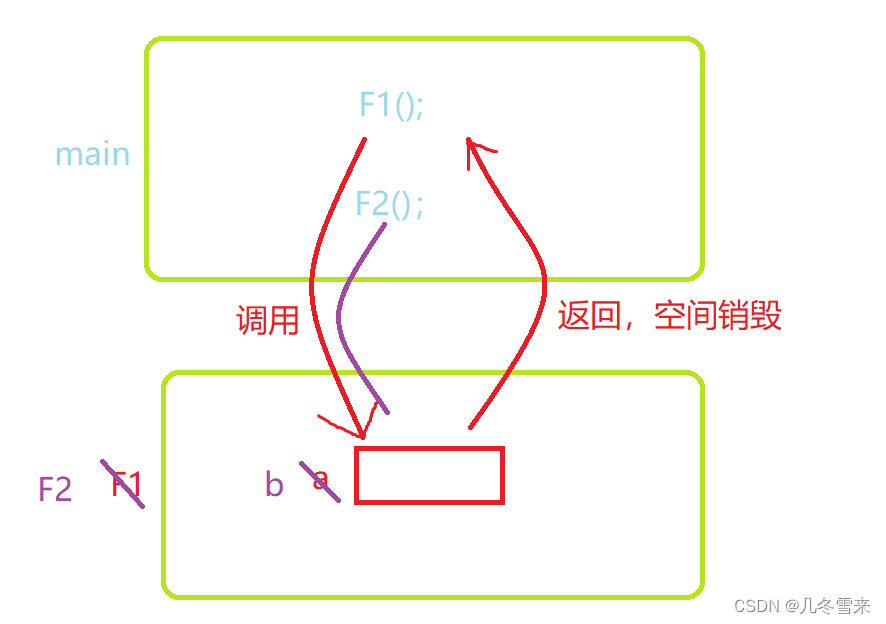
在我们这里一开始我们就调用了F1,调用完了F1之后,我们这里没有后续的操作,那么我们这里的F1运行结束,结束完了之后我们的栈帧就要进行销毁,空间销毁可以说是我们把使用权还给操作系统。 接下来我们要调用F2,因为在F1调用之后,我们将这块空间还给了操作系统,所以在创建F2的时候,我们又要向操作系统申请空间。这里操作系统就会给我们开辟一块空间命名为F2,在F2中我们又定义一个变量为b,因为我们的a和b执行的指令和内容基本一致,因此我们这块空间又被取了一个b的名字,这就导致了我们这里a和b的地址是一样的。
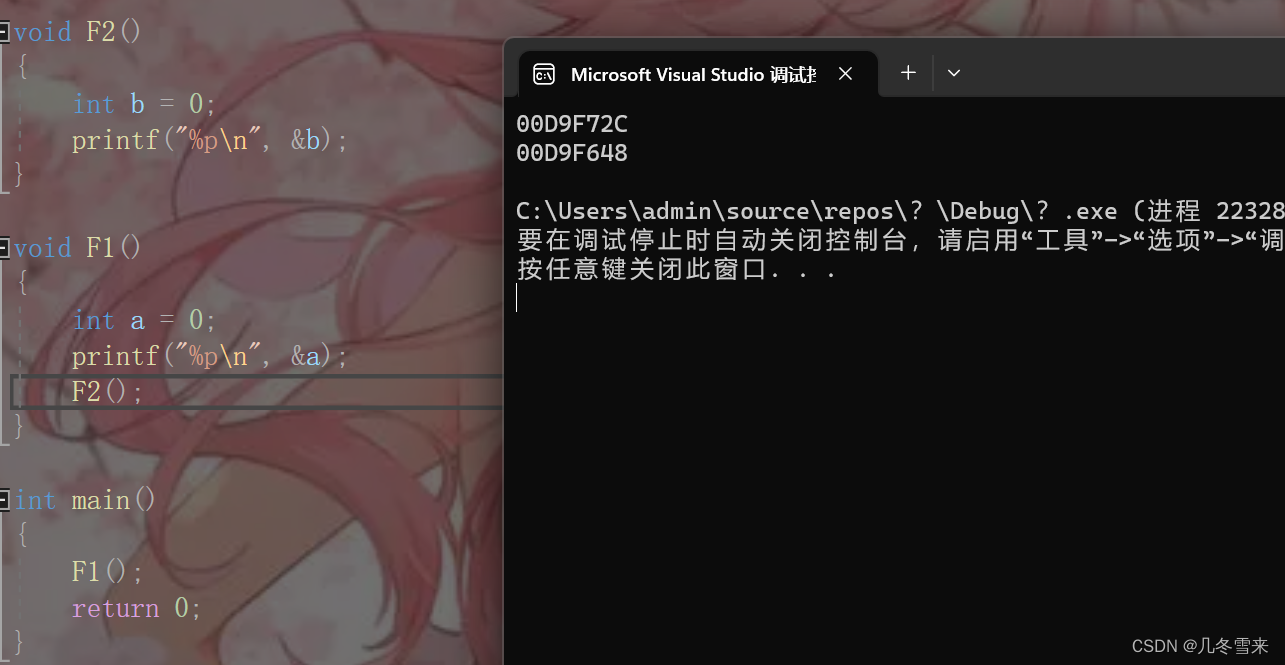
如果这里我们不想让它们共用同一块空间,和上面的代码不一样,在上面那个代码中,我们是调用完了F1之后再调用F2,而在这个代码中,我们是先调用F1,然后再在F1中调用F2,这是一种链式调用。
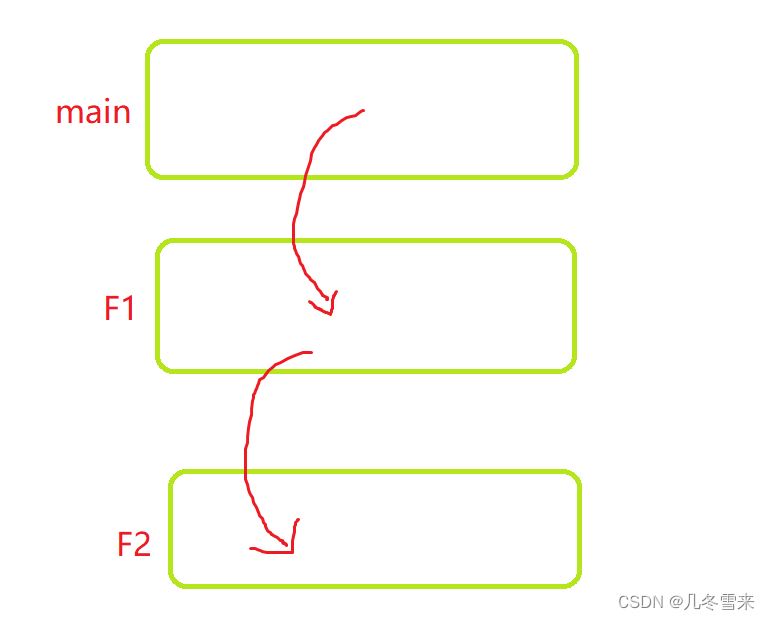
在我们第一种代码中的F1或者F2中多几个变量,也可能导致地址不一样。
结尾:
这篇博客基本将我们的数据结构的时间复杂度和空间复杂度都讲解完了,但是这并不意味着我们的算法效率那部分内容到这里就彻彻底底的结束了,在我们后面学习其他内容又或者是写题的时候,有的时候我们或多或少也会再次接触到我们的时间和空间复杂度,这篇博客是我返校上课的第一篇博客,可能是我个人没有适应学校的这种环境,导致我感觉自己写的博客有点乱,后面我会调整一下自己,希望这篇博客对大家能有所帮助。
相关文章:

数据结构——复杂度讲解(2)
作者:几冬雪来 时间:2023年2月22日 内容:数据结构复杂度讲解 目录 前言: 复杂度讲解(2): 1.空间复杂度是什么: 2.空间复杂度讲解: 结尾: 前言&#x…...
)
【LeetCode】任务调度器 [M](贪心)
621. 任务调度器 - 力扣(LeetCode) 一、题目 给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间&…...

Spring代理模式——静态代理和动态代理
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

Anaconda和PyCharm的一些安装问题和命令
今天更新了Windows上的Anaconda到2.3.2,PyCharm到2022.3。 ——发现是纯纯的犯贱orz。出了一堆问题。在这里记录一下供后来者参考。 Anaconda安装 将.\anaconda3\Scripts 和.\anaconda3\Library\bin添加到系统环境变量中。 新建环境的目录在.\anaconda3\envs下 N…...

sql优化建议
对查询进行优化,应尽量避免全表扫描,首先应考虑在 where 及 order by 涉及的列上建立索引。 应尽量避免在 where 子句中使用!或<>操作符,否则将引擎放弃使用索引而进行全表扫描。 应尽量避免在 where 子句中对字段进行 null 值判断&a…...

google hacker语句
哎,我就是沾边,就是不打实战( ̄o ̄) . z Z 文章目录前言一、什么是谷歌Docker?二、受欢迎的谷歌docker语句谷歌docker的例子日志文件易受攻击的 Web 服务器打开 FTP 服务器SSH私钥电子邮件列表实时摄像机MP3、电影和 PDF…...
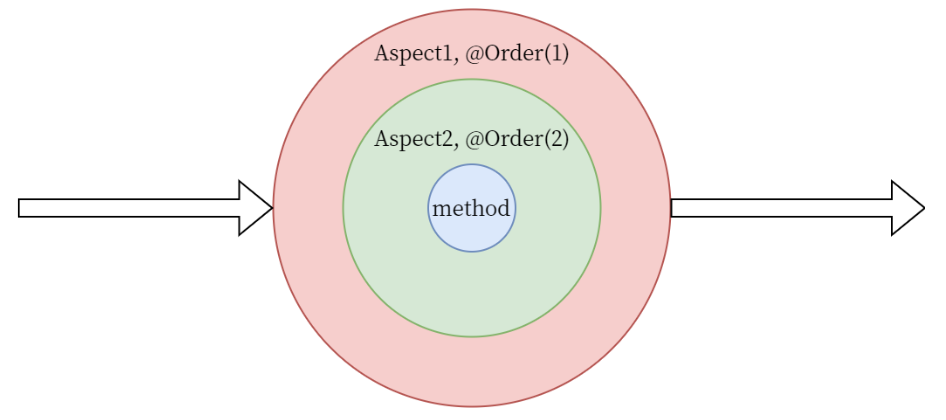
Spring AOP
Spring AOP 文章目录Spring AOP1.概念1.面向切面编程2.AOP的目的3.AOP实现的分类4.AOP 术语2. Spring AOP的特性1.能力与目标2.AOP机制1.理解SpringAOP的代理2.AOP代理类的自调用代码的粒度如何让自调用走代理?3.Enabling AspectJ Support3. 定义切面与切点1. 声明切…...

【消费战略方法论】认识消费者的恒常原理(一):消费者稳态平衡原理
“消费战略”是塔望咨询基于大量的战略与营销实践经验结合心理学、经济学、传播学等相关专业学科的知识应用进行提炼与创造形成的战略方法体系。消费战略强调以消费者为导向,进行企业、品牌战略、品牌营销的制订和落地,企业经营的每个环节和输出的每个动…...

python居然能语音控制电脑壁纸切换,只需60行代码
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 家在日常的电脑使用中,都会有自己喜爱类型的桌面 单纯的桌面有时候会让人觉得单调 今天,就由我带领大家只用60行代码打造一款语音壁纸切换器程序, 让大家能够通过语音的方式来控制电脑去…...

内存泄露定位手段(c语言hook malloc相关方式)
如何确定有内存泄露问题,如何定位到内存泄露位置,如何写一个内存泄漏检测工具? 1:概述 内存泄露本质:其实就是申请调用malloc/new,但是释放调用free/delete有遗漏,或者重复释放的问题。 内存…...
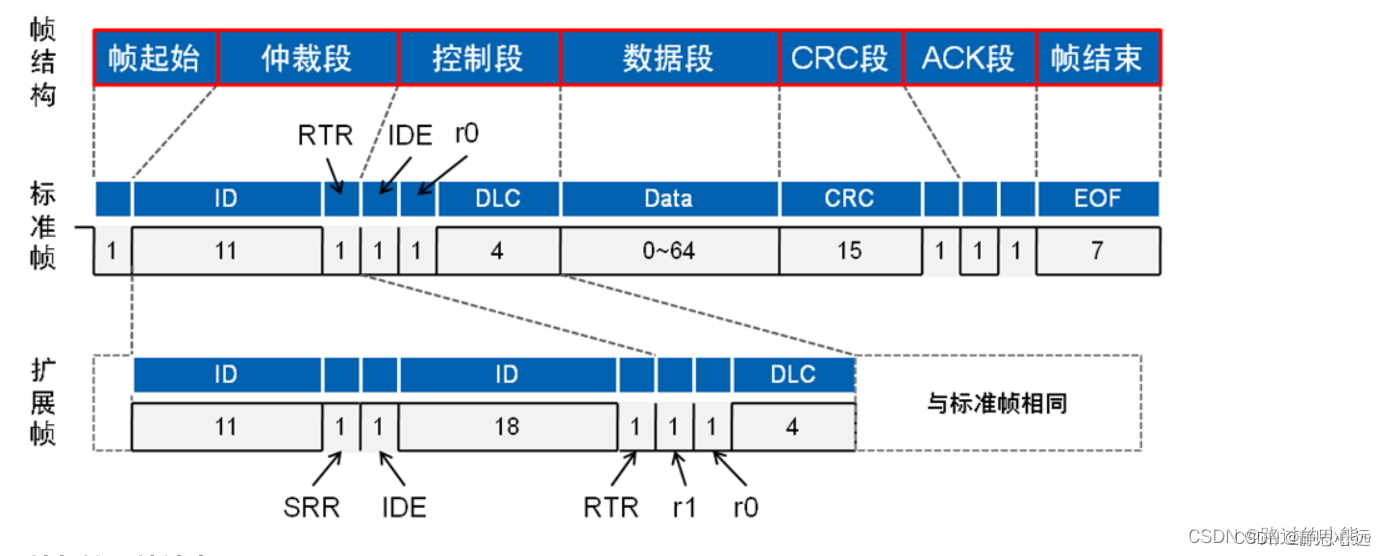
STM32 CAN波特率计算
STM32 CAN波特率计算简介CAN总线收发,中断方式接收配置代码部分reference简介 CAN通信帧共分为数据帧、远程帧、错误帧、过载帧和帧间隔,本文这里以数据帧为例。 显性电平对应逻辑0,CAN_H和CAN_L之差为2.5V左右。而隐性电平对应逻辑1&#x…...

C/C++ 中#define 的妙用,让代码更美一些
C/C 中#define 的妙用,让代码更美一些 flyfish 1 数值类型输出易读的字符串形式 例如使用enum定义一些错误值,想要将数值类型的错误,输出易读的字符串形式 重要的一句代码 #define MAKE_PAIR(val) std::make_pair(val, #val)可以看到 #va…...
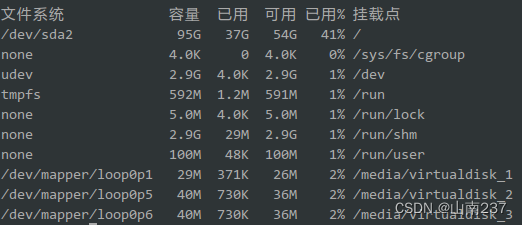
Linux文件系统操作与磁盘管理
查看磁盘和目录的容量 使用 df 命令查看磁盘的容量 df在实验楼的环境中你将看到如下的输出内容: 但在实际的物理主机上会更像这样: 物理主机上的 /dev/sda2 是对应着主机硬盘的分区,后面的数字表示分区号,数字前面的字母 a 表示…...

【Python】批量采集原神表情包~
嗨害大家好鸭~我是小熊猫(✿◡‿◡) 最近迷上了原神, 不自觉中就很喜欢保存广大旅行者制作的表情包~ 真的很有意思诶~ 源码资料电子书:点击此处跳转文末名片获取 一个个保存的话,好像效率很低嘛… 那我就发挥我小熊猫的老本行直接给把他们全部采集下…...

C语言基本语法注释类型关键字
C 基本语法 标识符 给变量所取的名字叫变量名,定义变量的名字需要遵循标识符的命名规则。 标识符是用来标识变量、符号常量、数组、函数、文件等名字的有效字符序列。 标识符的命名规则: 1.只能由字母、数字和下划线组成(例如:…...

【C ++】C++入门知识(二)
C入门(二) 作者:小卢 专栏:《C》 喜欢的话:世间因为少年的挺身而出,而更加瑰丽。 ——《人民日报》 1.引用 1.1.引用的概念及应用 引用(&) 引用不是新定义一个变量࿰…...

qt qchart学习
Qt Charts主要由QChartView、QChart、QLegend图例、坐标轴(由QAbstractAxis子类实现)、**数据源(由QAbstractSeries子类实现)**等组成使用QChart的前期准备1. Qt5.9及以上版本;2. .pro文件中添加QT charts3. 在使用QChart的各个控件之前,引用头文件并必…...
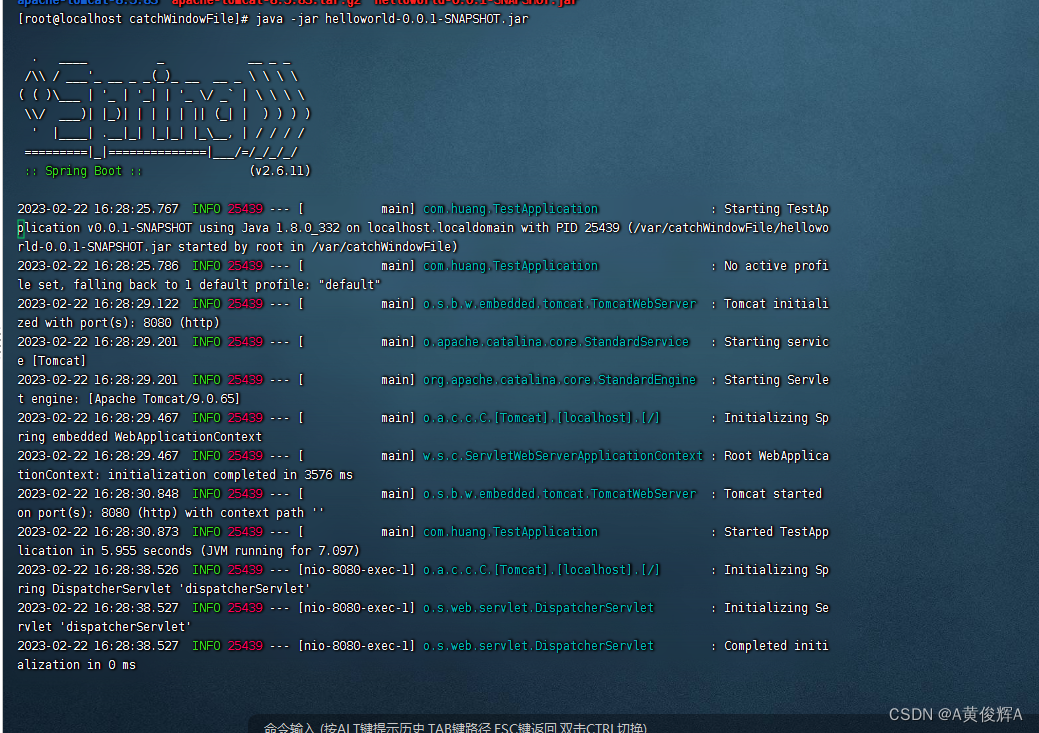
手工布署 java 项目
新建一个java springboot项目 maven 这是一个非常简易的 springBoot 的项目 使用 maven 的 package 工具进行打包 把包上传到 linux 的机器上, 确保 linux 机器上安装了 java jdk工具, 并且配置好了 JAVA_HOME 注意,helloworld 默认的是要使…...

《设计模式》观察者模式
《设计模式》观察者模式 观察者模式是一种行为型设计模式,它定义了一种一对多的依赖关系,让多个观察者对象可以同时监听和相应被观察者对象的状态变化,以达到解耦和复用的目的。观察者模式的优点如下: 解耦:观察者模…...
基于SpringBoot的外卖项目(详细开发过程)
基于SpringBootMyBatisPlus的外卖项目1、软件开发整体介绍软件开发流程角色分工2、外卖项目介绍项目介绍产品展示后台系统管理移动端技术选型功能结构角色3、开发环境的搭建开发环境说明建库建表Maven项目搭建项目的目录结构pom.xmlapplication.ymlReggieApplication启动类配置…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
