机器学习笔记之最优化理论与方法(十)无约束优化问题——共轭梯度法背景介绍
机器学习笔记之最优化理论与方法——共轭梯度法背景介绍
- 引言
- 背景:共轭梯度法
- 线性共轭梯度法
- 共轭方向
- 共轭VS正交
- 共轭方向法
- 共轭方向法的几何解释
引言
本节将介绍共轭梯度法,并重点介绍共轭方向法的逻辑与几何意义。
背景:共轭梯度法
关于最小化二次目标函数: min f ( x ) = min 1 2 x T Q x + C T x \begin{aligned}\min f(x) = \min \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x\end{aligned} minf(x)=min21xTQx+CTx,其中 Q ∈ R n × n ; Q ≻ 0 \mathcal Q \in \mathbb R^{n \times n};\mathcal Q \succ 0 Q∈Rn×n;Q≻0,且 C ∈ R n \mathcal C \in \mathbb R^n C∈Rn。很明显:由于 Q \mathcal Q Q是正定矩阵,那么该函数是凸二次函数。
关于该函数的最优解:令 ∇ f ( x ) ≜ 0 \nabla f(x) \triangleq 0 ∇f(x)≜0,有:
凸函数的局部最优解(极值点)也是它的全局最优解。
∇ f ( x ) = Q x + C ≜ 0 \nabla f(x) = \mathcal Q x + \mathcal C \triangleq 0 ∇f(x)=Qx+C≜0
可以看出: Q x + C = 0 \mathcal Q x + \mathcal C = 0 Qx+C=0是一个包含 n n n个方程的线性方程组。
- 如果 n n n的规模较小时,关于解方程组,可以使用其他工具进行解决。例如:高斯消去法;
- 相反,当 n n n的规模较大时,对应的增广矩阵规模同样很大,使用高斯消去法解方程组的成本较高。
而共轭梯度法初始就是针对方程组的一种迭代求解方法。随着最优化问题的推广,关于目标函数 f ( x ) f(x) f(x)也不仅仅局限在二次函数。对于这类 min f ( x ) \min f(x) minf(x)的方法也被称作非线性共轭梯度法。
对于上述方程组问题的迭代求解方法也被称作线性共轭梯度法。
线性共轭梯度法
关于上述优化问题: min f ( x ) = 1 2 x T Q x + C T x ; Q ≻ 0 \begin{aligned}\min f(x) = \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x;\mathcal Q \succ 0\end{aligned} minf(x)=21xTQx+CTx;Q≻0
- 假设正定矩阵 Q \mathcal Q Q是一个对角矩阵 B = ( b 1 b 2 ⋱ b n ) n × n \mathcal B = \begin{pmatrix} b_1 & \quad & \quad & \quad \\ \quad & b_2 & \quad & \quad\\ \quad & \quad & \ddots & \quad \\ \quad & \quad & \quad & b_n \end{pmatrix}_{n \times n} B= b1b2⋱bn n×n,那么此时可以发现: f ( x ) = 1 2 x T B x + C T x \begin{aligned}f(x) = \frac{1}{2}x^T \mathcal B x + \mathcal C^T x \end{aligned} f(x)=21xTBx+CTx中的二次项部分仅包含 x x x内各分量的平方项,而不包含各分量的交叉项;
以n = 2 n=2 n=2为例,对应目标函数图像以及在x 1 , x 2 x_1,x_2 x1,x2方向上的投影(等值线)示例如下。

很明显,可以看出:描述等值线的椭圆,其长轴与短轴分别与坐标轴平行。如果通过迭代的方式进行求解,可以根据无约束优化问题——常用求解方法(上)中介绍的坐标轴交替下降法进行求解。图像表示如下:
由于更新方向被确定——与坐标轴方向平行。因此仅需要计算各维度达到最小步长即可。因而仅需要2 2 2步就可以找到最优解。

同理,如果是 x ∈ R n x \in \mathbb R^n x∈Rn,需要将所有的轴均迭代一遍即可找到最优解。 - 如果 Q \mathcal Q Q是一个一般形式的正定矩阵: Q = ( q 11 q 12 ⋯ q 1 n q 21 q 22 ⋯ q 2 n ⋮ ⋮ ⋱ ⋮ q n 1 q n 2 ⋯ q n n ) n × n ; Q ≻ 0 \mathcal Q = \begin{pmatrix} q_{11} & q_{12} & \cdots & q_{1n} \\ q_{21} & q_{22} & \cdots & q_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ q_{n1} & q_{n2} & \cdots & q_{nn} \end{pmatrix}_{n \times n};\mathcal Q \succ 0 Q= q11q21⋮qn1q12q22⋮qn2⋯⋯⋱⋯q1nq2n⋮qnn n×n;Q≻0。这里依然以 n = 2 n=2 n=2为例,对应的目标函数 f ( x ) f(x) f(x)在决策变量 x x x各分量的等值线示例如下:
由于交叉项q m n ( m ≠ n ) q_{mn}(m \neq n) qmn(m=n)的存在,对应椭圆图像的长轴与短轴不再与坐标轴平行。

针对这种一般情况的二次型函数 min f ( x ) = 1 2 x T Q x + C T x \begin{aligned}\min f(x) = \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x\end{aligned} minf(x)=21xTQx+CTx,可以通过二次型的线性替换,从而将函数转化为标准型函数:
其中D \mathcal D D是由Q \mathcal Q Q特征值组成的对角阵;而P \mathcal P P则表示由特征值对应特征向量组成的正交阵。
Q = P T D P D = ( λ 1 λ 2 ⋱ λ n ) n × n \mathcal Q = \mathcal P^T \mathcal D \mathcal P \quad \mathcal D = \begin{pmatrix} \lambda_1 & \quad & \quad & \\ \quad & \lambda_2 &\quad & \\ \quad & \quad & \ddots & \\ \quad & \quad & \quad & \lambda_n \end{pmatrix}_{n \times n} Q=PTDPD= λ1λ2⋱λn n×n
替换后的函数 f ( x ) f(x) f(x)可表示为:
记x ^ = P x \hat {x} = \mathcal P x x^=Px反之x = P T x ^ x = \mathcal P^T \hat x x=PTx^。
f ( x ) = 1 2 x T Q x + C T x = 1 2 x T P T D P x + C T x = 1 2 ( P x ) T D ( P x ) + C T x = 1 2 [ x ^ ] T D x ^ + C T ( P T x ^ ) = 1 2 [ x ^ ] T D x ^ + ( P C ) T x ^ = f ^ ( x ^ ) \begin{aligned} f(x) & = \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x \\ & = \frac{1}{2} x^T \mathcal P^T \mathcal D \mathcal P x + \mathcal C^T x \\ & = \frac{1}{2}(\mathcal P x)^T \mathcal D (\mathcal P x) + \mathcal C^T x \\ & = \frac{1}{2} [\hat x]^T \mathcal D \hat {x} +\mathcal C^T (\mathcal P^T \hat x )\\ & = \frac{1}{2} [\hat x]^T \mathcal D \hat {x} + (\mathcal P \mathcal C)^T \hat x \\ & = \hat {f}(\hat x) \end{aligned} f(x)=21xTQx+CTx=21xTPTDPx+CTx=21(Px)TD(Px)+CTx=21[x^]TDx^+CT(PTx^)=21[x^]TDx^+(PC)Tx^=f^(x^)
此时,该公式又变回了第一类标准型。同样可以通过坐标轴交替下降法对新目标函数 f ^ ( x ^ ) \hat f(\hat x) f^(x^)进行求解。如果找到了关于 x ^ \hat x x^的最优解,可以通过 x = P T x ^ x = \mathcal P^T \hat x x=PTx^找到 x x x的最优解。
而线性共轭梯度法是用来针对线性方程组 ∇ f ( x ) = Q x + C ≜ 0 \nabla f(x) = \mathcal Q x + \mathcal C \triangleq 0 ∇f(x)=Qx+C≜0的求解问题。如果针对上述逻辑,必然需要先将正交矩阵 P \mathcal P P求解出来。但相反,由于 P \mathcal P P是由特征值对应特征向量组成的正交矩阵,而求解特征向量依然要解方程组 Q x + C ≜ 0 \mathcal Q x + \mathcal C \triangleq 0 Qx+C≜0。
很明显,这形成了一个闭环:想要通过 P \mathcal P P求解方程组,而 P \mathcal P P自身也要通过求解方程组来获取。
而共轭梯度法的思路是:想要通过获取一系列的 n n n维向量: d 0 , d 1 , ⋯ , d n − 1 ∈ R n d_0,d_1,\cdots,d_{n-1} \in \mathbb R^n d0,d1,⋯,dn−1∈Rn,其组成的矩阵 S = ( d 0 , d 1 , ⋯ , d n − 1 ) n × n \mathcal S = (d_0,d_1,\cdots,d_{n-1})_{n \times n} S=(d0,d1,⋯,dn−1)n×n,使其替代上面描述的正交矩阵 P n × n \mathcal P_{n \times n} Pn×n,从而帮助 Q \mathcal Q Q完成对角化:
Q = S T D S \mathcal Q = \mathcal S^T \mathcal D \mathcal S Q=STDS
从而通过上述思路,求解最优解: x = S T x ^ x = \mathcal S^T \hat {x} x=STx^。
关于向量组: d 0 , d 1 , ⋯ , d n − 1 d_0,d_1,\cdots,d_{n-1} d0,d1,⋯,dn−1,向量之间的关系被定义为共轭关系。
共轭方向
共轭方向的定义表示为:考虑正定矩阵 Q \mathcal Q Q以及非零向量 d i , d j ( i ≠ j ) d_i,d_j(i \neq j) di,dj(i=j),若满足:
( d i ) T Q d j = 0 (d_i)^T \mathcal Q d_j = 0 (di)TQdj=0
则称向量 d i , d j d_i,d_j di,dj关于矩阵 Q \mathcal Q Q共轭。如果向量组 D = { d 0 , d 1 , ⋯ , d k } \mathcal D = \{d_0,d_1,\cdots,d_k\} D={d0,d1,⋯,dk}关于矩阵 Q \mathcal Q Q共轭,即向量之间两两共轭:
∀ d i , d j ∈ D ; i ≠ j ⇒ ( d i ) T Q d j = 0 \forall d_i,d_j \in \mathcal D;i \neq j \Rightarrow (d_i)^T \mathcal Q d_j = 0 ∀di,dj∈D;i=j⇒(di)TQdj=0
共轭VS正交
根据上述共轭梯度法的思路,以及共轭方向定义的描述,观察:共轭与正交之间的关系。
-
如果向量组 D { d 0 , d 1 , ⋯ , d k } \mathcal D \{d_0,d_1,\cdots,d_k\} D{d0,d1,⋯,dk}关于单位矩阵 I \mathcal I I共轭:此时向量 d i , d j ∈ D d_i,d_j \in \mathcal D di,dj∈D之间的共轭关系退化为正交关系:
∀ d i , d j ∈ D , i ≠ j ( d i ) T I d j = 0 ⇒ ( d i ) T d j = 0 \forall d_i,d_j \in \mathcal D,i \neq j \quad (d_i)^T \mathcal Id_j = 0 \Rightarrow (d_i)^T d_j = 0 ∀di,dj∈D,i=j(di)TIdj=0⇒(di)Tdj=0 -
如果向量组 D { d 0 , d 1 , ⋯ , d k } \mathcal D \{d_0,d_1,\cdots,d_k\} D{d0,d1,⋯,dk}关于正定矩阵 Q \mathcal Q Q共轭:令 Q = M T Λ M \mathcal Q = \mathcal M^T \Lambda \mathcal M Q=MTΛM,并令 Λ = λ 2 \Lambda = \lambda^2 Λ=λ2,有:
由于M \mathcal M M是正交矩阵:M M T = I \mathcal M \mathcal M^T = \mathcal I MMT=I,因而可以在展开过程中插入一个M M T \mathcal M \mathcal M^T MMT。令P = M T λ M \mathcal P = \mathcal M^T \lambda \mathcal M P=MTλM
Q = M T Λ M = M T λ 2 M = ( M T λ M ) ( M T λ M ) = ( M T λ M ) 2 = P 2 \begin{aligned} \mathcal Q & = \mathcal M^T \Lambda \mathcal M \\ & = \mathcal M^T \lambda^2 \mathcal M \\ & = (\mathcal M^T\lambda \mathcal M) (\mathcal M^T \lambda \mathcal M) \\ & = (\mathcal M^T \lambda \mathcal M)^2 \\ & = \mathcal P^2 \end{aligned} Q=MTΛM=MTλ2M=(MTλM)(MTλM)=(MTλM)2=P2
从而将 Q \mathcal Q Q分解成 P 2 \mathcal P^2 P2的形式。并且 P = M T λ M \mathcal P = \mathcal M^T \lambda \mathcal M P=MTλM也是一个正定矩阵: P 2 = P ⋅ P = P T P \mathcal P^2 = \mathcal P \cdot \mathcal P = \mathcal P^T \mathcal P P2=P⋅P=PTP。
关于向量 d i , d j d_i,d_j di,dj共轭: ( d i ) T Q d j = 0 (d_i)^T \mathcal Q d_j = 0 (di)TQdj=0可表示为:
( d i ) T Q d j = ( d i ) T P 2 d j = ( d i ) T P T P d j = ( P d i ) T ( P d j ) = 0 \begin{aligned} (d_i)^T \mathcal Q d_j & = (d_i)^T \mathcal P^2 d_j \\ & = (d_i)^T \mathcal P^T \mathcal P d_j \\ & = (\mathcal P d_i)^T (\mathcal P d_j) = 0 \end{aligned} (di)TQdj=(di)TP2dj=(di)TPTPdj=(Pdi)T(Pdj)=0
也就是说:向量 d i , d j d_i,d_j di,dj经过正交矩阵 P \mathcal P P的投影结果: P d i , P d j \mathcal Pd_i,\mathcal Pd_j Pdi,Pdj之间是正交关系。
关于向量投影的描述详见主成分分析(最大投影方差) -
根据正交的性质,两两正交的向量组,其内部向量必然线性无关;两两共轭的向量组,其内部向量同样线性无关。由于决策变量 x ∈ R n x \in \mathbb R^n x∈Rn,因而对应的两两共轭向量组内最多包含 n n n个两两共轭的向量。
再多一个,必然出现向量之间不共轭的情况。
共轭方向法
依然针对凸二次函数的优化问题: min f ( x ) = 1 2 x T Q x + C T x , Q ≻ 0 \begin{aligned}\min f(x) = \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x,\mathcal Q \succ 0 \end{aligned} minf(x)=21xTQx+CTx,Q≻0,通过迭代的方式求解 x x x的最优解:
- 给定:初始点 x 0 x_0 x0以及一组关于 Q \mathcal Q Q的共轭方向 d 0 , d 1 , ⋯ , d n − 1 d_0,d_1,\cdots,d_{n-1} d0,d1,⋯,dn−1,令:
与坐标轴交替下降法的思路如出一辙,只不过方向选择由原来两两正交的坐标轴作为方向替换为两两共轭的向量作为方向。
x k + 1 = x k + α k ⋅ d k x_{k+1} = x_k + \alpha_k \cdot d_k xk+1=xk+αk⋅dk - 其中 α k \alpha_k αk满足:
即当前迭代步骤的最优解,之所以选择最优解,因为该函数是凸函数,对应的最优解必然是全局最优解。
α k = arg min α ϕ ( α ) = arg min α f ( x k + α ⋅ d k ) \alpha_k = \mathop{\arg\min}\limits_{\alpha} \phi(\alpha) = \mathop{\arg\min}\limits_{\alpha} f(x_k + \alpha \cdot d_k) αk=αargminϕ(α)=αargminf(xk+α⋅dk)
计算 ∇ ϕ ( α k ) ≜ 0 \nabla \phi(\alpha_k) \triangleq 0 ∇ϕ(αk)≜0,有:
∇ ϕ ( α k ) = f ( x k + α k ⋅ d k ) T d k = [ Q ( x k + α k ⋅ d k ) + C ] T d k = ( Q x k + C ) T d k + α k ( x k ) T Q d k ≜ 0 \begin{aligned} \nabla \phi(\alpha_k) & = f(x_k + \alpha_k \cdot d_k)^T d_k \\ & = [\mathcal Q(x_k + \alpha_k \cdot d_k) + \mathcal C]^T d_k \\ & = (\mathcal Q x_k + \mathcal C)^T d_k + \alpha_k (x_k)^T \mathcal Q d_k \triangleq 0 \\ \end{aligned} ∇ϕ(αk)=f(xk+αk⋅dk)Tdk=[Q(xk+αk⋅dk)+C]Tdk=(Qxk+C)Tdk+αk(xk)TQdk≜0
最终有:
α k = − ( Q x k + C ) T d k ( d k ) T Q d k = − [ ∇ f ( x k ) ] T d k ( d k ) T Q d k \alpha_k = -\frac{(\mathcal Q x_k + \mathcal C)^T d_k}{(d_k)^T \mathcal Q d_k} = -\frac{[\nabla f(x_k)]^T d_k}{(d_k)^T \mathcal Q d_k} αk=−(dk)TQdk(Qxk+C)Tdk=−(dk)TQdk[∇f(xk)]Tdk
整个的算法过程并不麻烦,但需要一个前提:将共轭方向 d 0 , d 1 , ⋯ , d n − 1 d_0,d_1,\cdots,d_{n-1} d0,d1,⋯,dn−1提前给出。因而不同共轭方向的选择方式对应其相应的共轭方向法。
与牛顿法的描述相似:针对 Hessian Matrix \text{Hessian Matrix} Hessian Matrix可能不是正定矩阵的一类情况,分为修正法, SR-1,DFP,BFGS \text{SR-1,DFP,BFGS} SR-1,DFP,BFGS等等方法;同理,共轭方向法为一类方法,而共轭梯度法只是其中一种方法。
共轭方向法的几何解释
观察关于初始点 x 0 x_0 x0的第一次迭代: x 0 ⇒ x 1 x_0 \Rightarrow x_1 x0⇒x1:
x 1 = x 0 + ∑ i = 0 n − 1 α i ⋅ d i x_1 = x_0 + \sum_{i=0}^{n-1} \alpha_i \cdot d_i x1=x0+i=0∑n−1αi⋅di
如果将 n n n个共轭方向组成矩阵,记作 S = ( d 0 , d 1 , ⋯ , d n − 1 ) n × n \mathcal S = (d_0,d_1,\cdots,d_{n-1})_{n \times n} S=(d0,d1,⋯,dn−1)n×n,由于共轭方向两两线性无关,因而 S \mathcal S S必然是可逆矩阵。该矩阵存在如下性质:
- 关于 S T Q S = [ ( d 0 ) T ⋮ ( d n − 1 ) T ] Q ( d 0 , ⋯ , d n − 1 ) = [ ( d i ) T Q d j ] n × n \mathcal S^T \mathcal Q \mathcal S = \begin{bmatrix} (d_0)^T \\ \vdots \\ (d_{n-1})^T \end{bmatrix} \mathcal Q (d_0,\cdots,d_{n-1}) = [(d_i)^T \mathcal Q d_j]_{n \times n} STQS= (d0)T⋮(dn−1)T Q(d0,⋯,dn−1)=[(di)TQdj]n×n,根据共轭方向的定义,当 i ≠ j i \neq j i=j时,必然有: ( d i ) T Q d j = 0 (d_i)^T \mathcal Q d_j = 0 (di)TQdj=0;相反,当 i = j i = j i=j时,由于 Q \mathcal Q Q是正定矩阵,因而 ( d i ) T Q d j > 0 (d_i)^T \mathcal Q d_j >0 (di)TQdj>0恒成立。从而 S T Q S \mathcal S^T \mathcal Q \mathcal S STQS不仅是一个正定矩阵,甚至是一个对角阵。
从而达到利用S \mathcal S S对Q \mathcal Q Q进行对角化的目的。 - 由于 S \mathcal S S可逆,根据逆矩阵的性质,必然有: S − 1 S = S − 1 ( d 0 , d 1 , ⋯ , d n − 1 ) = I \mathcal S^{-1} \mathcal S = \mathcal S^{-1}(d_0,d_1,\cdots,d_{n-1}) = \mathcal I S−1S=S−1(d0,d1,⋯,dn−1)=I(单位矩阵)。将该式展开,有:
I = S − 1 ( d 0 , d 1 , ⋯ , d n − 1 ) = ( S − 1 d 0 , S − 1 d 1 ⋯ S − 1 d n − 1 ) \begin{aligned} \mathcal I & = \mathcal S^{-1}(d_0,d_1,\cdots,d_{n-1}) \\ & = (\mathcal S^{-1} d_0,\mathcal S^{-1} d_1 \cdots \mathcal S^{-1} d_{n-1}) \end{aligned} I=S−1(d0,d1,⋯,dn−1)=(S−1d0,S−1d1⋯S−1dn−1)
其中展开后矩阵中的元素 S − 1 d i ( i = 0 , 1 , 2 , ⋯ , n − 1 ) \mathcal S^{-1} d_i(i=0,1,2,\cdots,n-1) S−1di(i=0,1,2,⋯,n−1)表示单位坐标向量 e i + 1 = ( 0 , 0 , ⋯ , 1 ⏟ i + 1 , ⋯ , 0 ) T e_{i+1} = (0,0,\cdots,\underbrace{1}_{i+1},\cdots,0)^T ei+1=(0,0,⋯,i+1 1,⋯,0)T
如果将决策变量 x = S ⋅ x ^ x = \mathcal S \cdot \hat {x} x=S⋅x^或者 x ^ = S − 1 x \hat x = \mathcal S^{-1} x x^=S−1x,从而原始目标函数 f ( x ) = 1 2 x T Q x + C T x \begin{aligned}f(x) = \frac{1}{2} x^T \mathcal Q x + \mathcal C^T x\end{aligned} f(x)=21xTQx+CTx可替换为一个新函数 f ^ ( x ^ ) \hat f(\hat {x}) f^(x^):
f ^ ( x ^ ) = 1 2 [ x ^ ] T S T Q S ⏟ 对角阵 ⋅ x ^ + ( S T C ) T x ^ \hat f(\hat {x}) = \frac{1}{2} [\hat x]^T \underbrace{\mathcal S^T \mathcal Q \mathcal S}_{对角阵} \cdot \hat {x} + (\mathcal S^T \mathcal C)^T \hat {x} f^(x^)=21[x^]T对角阵 STQS⋅x^+(STC)Tx^
此时的新函数中仅包含关于 x ^ i ( i = 1 , 2 , ⋯ , n ) \hat {x}_i(i=1,2,\cdots,n) x^i(i=1,2,⋯,n)的平方项,而没有交叉项。从而新函数 f ^ ( x ^ ) \hat f(\hat x) f^(x^)在 x ^ \hat x x^特征空间中的等值线依然是一个椭圆/椭球/超椭球,其长轴与短轴同样与坐标轴平行。
回归第一次迭代: x 0 + ∑ i = 0 n − 1 α i ⋅ d i x_0 + \sum_{i=0}^{n-1} \alpha_i \cdot d_i x0+∑i=0n−1αi⋅di,这明显是一个在原始特征空间 x x x上的操作。如果该操作映射在 x ^ \hat x x^的特征空间中会变成什么样的效果 ? ? ?
只需要将 x x x特征空间中的正交向量乘以 S − 1 \mathcal S^{-1} S−1即可得到对应 x ^ \hat x x^特征空间的正交向量。
S − 1 x 0 + α 0 S − 1 d 0 + α 1 S − 1 d 1 + ⋯ + α n − 1 S − 1 d n − 1 \mathcal S^{-1}x_0 + \alpha_0 \mathcal S^{-1}d_0 + \alpha_1 \mathcal S^{-1} d_1 + \cdots + \alpha_{n-1} \mathcal S^{-1} d_{n-1} S−1x0+α0S−1d0+α1S−1d1+⋯+αn−1S−1dn−1
由于 e i + 1 = S − 1 d i ( i = 1 , 2 , ⋯ , n − 1 ) e_{i+1} = \mathcal S^{-1} d_i(i=1,2,\cdots,n-1) ei+1=S−1di(i=1,2,⋯,n−1),整理有:
很明显,在 x ^ \hat x x^的特征空间中,相当于坐标轴交替下降法,沿着坐标轴进行搜索。
S − 1 x 0 + α 0 e 1 + α 1 e 2 + ⋯ + α n − 1 e n \mathcal S^{-1}x_0 + \alpha_0 e_1 + \alpha_1 e_2 + \cdots + \alpha_{n-1} e_{n} S−1x0+α0e1+α1e2+⋯+αn−1en
下一节将继续介绍共轭方向法。
0 : 37 : 14 / 1 : 26 : 29 0:37:14/1:26:29 0:37:14/1:26:29
Reference \text{Reference} Reference:
最优化理论与方法-第七讲-无约束优化问题(三)
相关文章:

机器学习笔记之最优化理论与方法(十)无约束优化问题——共轭梯度法背景介绍
机器学习笔记之最优化理论与方法——共轭梯度法背景介绍 引言背景:共轭梯度法线性共轭梯度法共轭方向共轭VS正交共轭方向法共轭方向法的几何解释 引言 本节将介绍共轭梯度法,并重点介绍共轭方向法的逻辑与几何意义。 背景:共轭梯度法 关于…...

Mybatis核心对象及工作流程
目录 一、mybatis核心对象 (1)SqlSession对象直接操作数据库 (2)SqlSession对象通过代理对象操作数据库 二、mybatis工作流程 一、mybatis核心对象 (1)SqlSessionFactoryBuilder SqlSession工厂构建者对…...
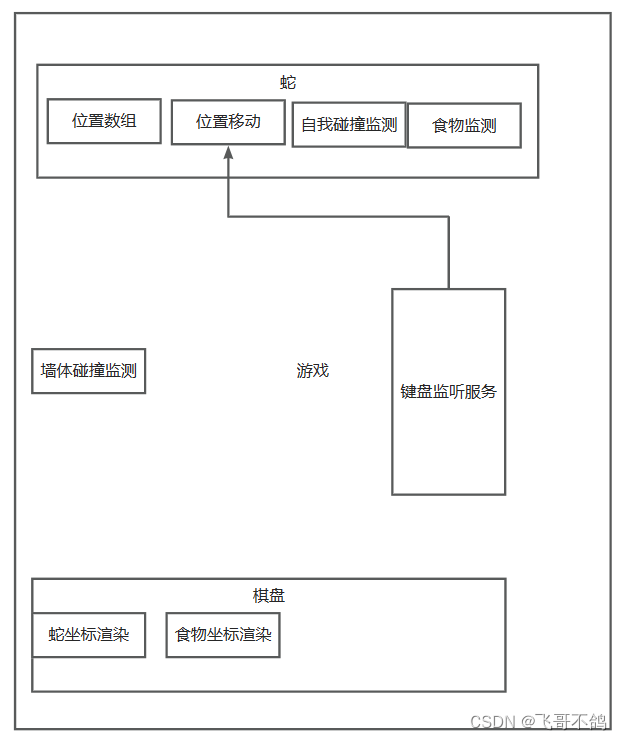
无swing,高级javaSE毕业之贪吃蛇游戏(含模块构建,多线程监听服务),已录制视频
JavaSE,无框架实现贪吃蛇 B站已发视频:无swing,纯JavaSE贪吃蛇游戏设计构建 文章目录 JavaSE,无框架实现贪吃蛇1.整体思考2.可能的难点思考2.1 如何表示游戏界面2.2 如何渲染游戏界面2.3 如何让游戏动起来2.4 蛇如何移动 3.流程图…...
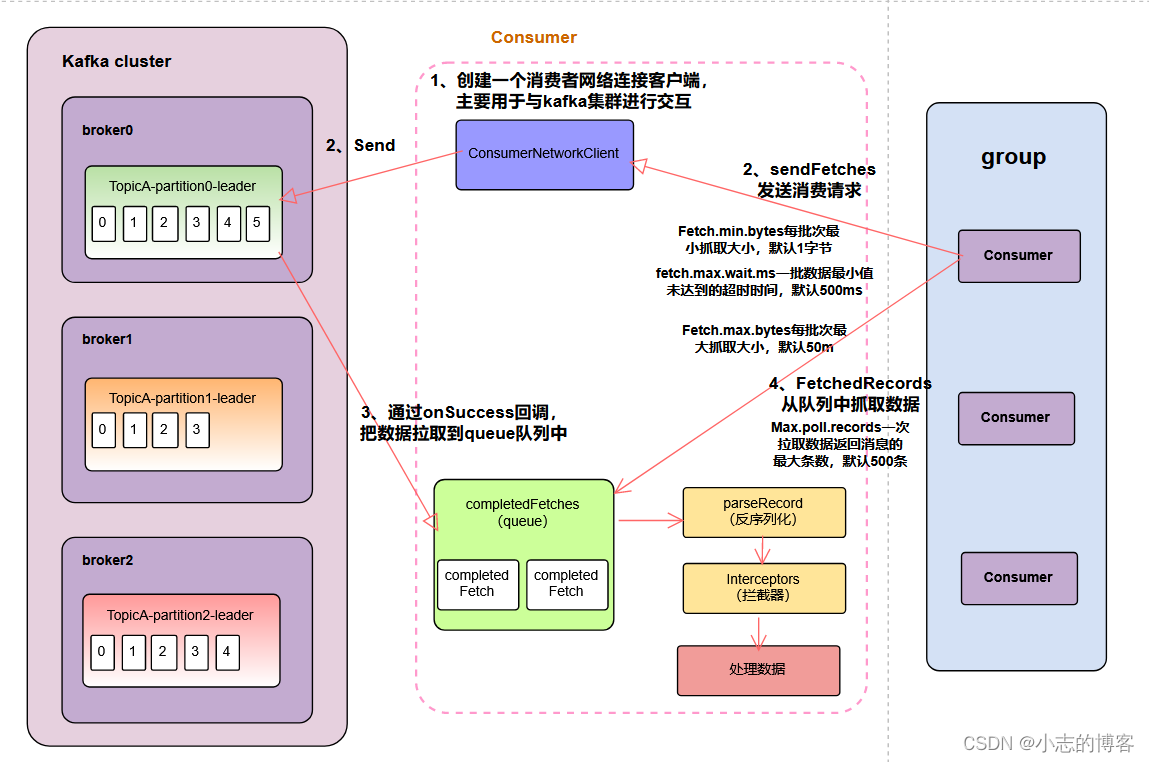
Kafka3.0.0版本——消费者(消费者组详细消费流程图解及消费者重要参数)
目录 一、消费者组详细消费流程图解二、消费者的重要参数 一、消费者组详细消费流程图解 创建一个消费者网络连接客户端,主要用于与kafka集群进行交互,如下图所示: 调用sendFetches发送消费请求,如下图所示: (1)、Fet…...

算法通关村-----位运算在海量元素中查找重复元素的妙用
用4KB内存寻找重复元素 问题描述 给定一个数组,包含从1到N的整数,N最大为32000,数组可能还有重复值,且N的取值不定,若只有4KB内存可用,如何打印数组中所有的重复元素。 问题分析 Java中存储整数使用int…...

RabbitMQ: Publish/Subscribe结构
生产者 package com.qf.mq2302.publishSub;import com.qf.mq2302.utils.MQUtils;import com.rabbitmq.client.Channel; import com.rabbitmq.client.Connection;public class EmitLog {private static final String EXCHANGE_NAME "logs";public static void main…...

单片机-蜂鸣器
简介 蜂鸣器是一种一体化结构的电子讯响器,采用直流电压供电 蜂鸣器主要分为 压电式蜂鸣器 和 电磁式蜂鸣器 两 种类型。 压电式蜂鸣器 主要由多谐振荡器、压电蜂鸣片、阻抗匹配器及共鸣箱、外壳等组成。多谐振荡器由晶体管或集成电路构成,当接通电源后&…...

华为云云耀云服务器L实例评测 | 分分钟完成打地鼠小游戏部署
前言 在上篇文章【华为云云耀云服务器L实例评测 | 快速部署MySQL使用指南】中,我们已经用【华为云云耀云服务器L实例】在命令行窗口内完成了MySQL的部署并简单使用。但是后台有小伙伴跟我留言说,能不能用【华为云云耀云服务器L实例】来实现个简单的小游…...

Android——数据存储(二)(二十二)
1. SQLite数据库存储 1.1 知识点 (1)了解SQLite数据库的基本作用; (2)掌握数据库操作辅助类:SQLiteDatabase的使用; (3)可以使用命令操作SQLite数据库; …...

appium环境搭建
一.appium环境搭建 1.python3 python3的下载安装这里就不多做介绍了,当然你也可以选择自己喜欢的语音,比如java… 2.jdk 1)下载地址 官网(需登录账号): https://www.oracle.com/java/technologies/downloads/ 百度网盘&…...
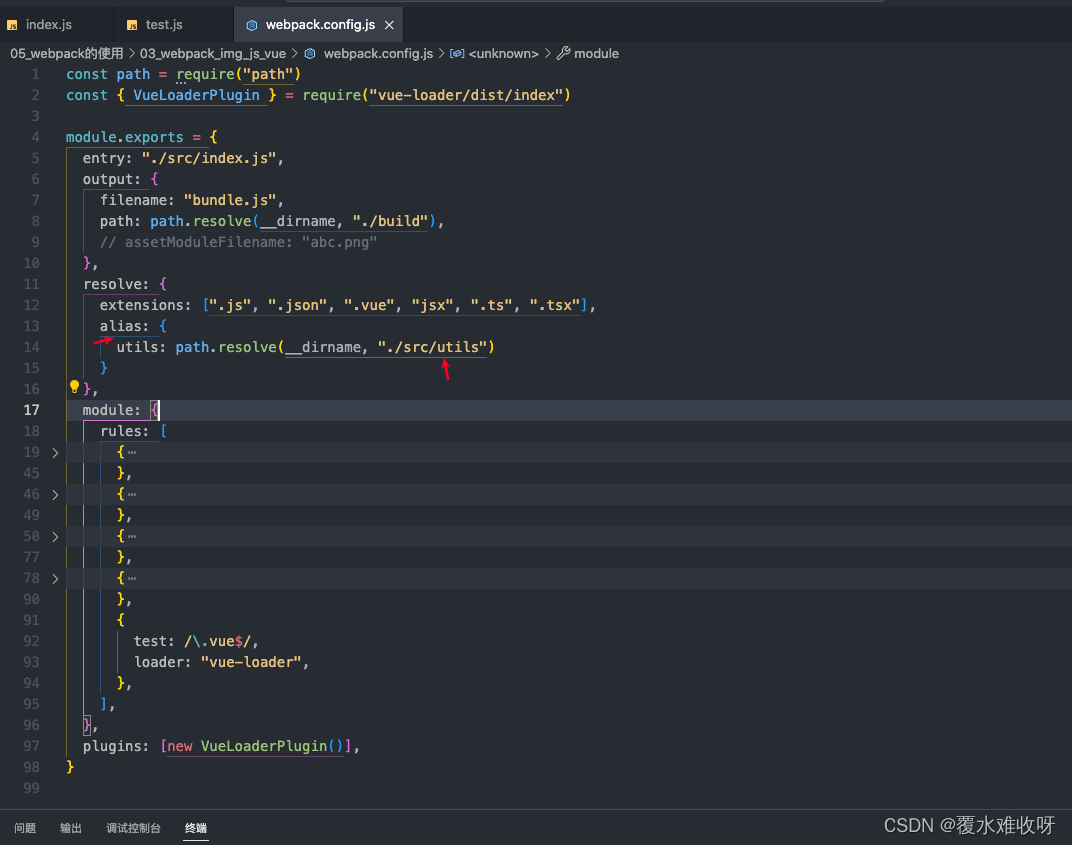
十五、Webpack打包图片-js-Vue、Label命令、resolve模块解析
一、webpack打包图片 (1)加载图片案例准备 为了演示我们项目中可以加载图片,我们需要在项目中使用图片,比较常见的使用图片的方式是两种: img元素,设置src属性;其他元素(比如div&…...

ARM指令集--数据处理指令
数据处理指令:数学运算,逻辑运算 立即数 立即数的本质 就是包含在指令当中的数,属于指令的一部分 立即数的优点:取指的时候就可以将其读取到CPU,不用单独去内存读取,速度快 立即数的缺点:不…...

Excel embed into a webpage
无法编辑嵌入式 Excel 网页版 工作簿,但具有适当权限的人员可能能够在 Excel 中打开嵌入的工作簿,他们可以在其中编辑数据。 通过制作一个浏览器,打开并编辑它 https://onedrive.live.com/embed? resid5FC97855340825A9%21135& aut…...
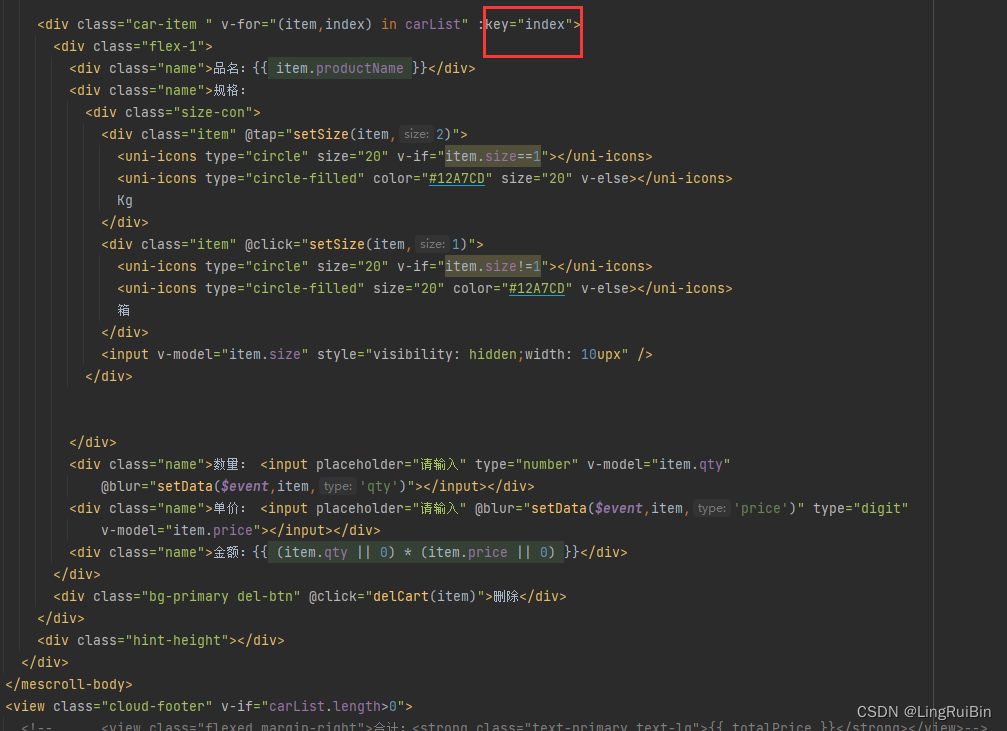
uniapp点击事件在小程序中无法传参
这个问题很是神奇,第一次遇到。在h5中,点击事件可以正常传参,打包小程序后确失效了。 修改:for循环中的key,使用 index就好了...

ssprompt:一个LLM Prompt分发管理工具
阅读顺序 🌟前言🔔ssprompt介绍命令介绍Metafile介绍版本依赖规则 🌊 PromptHubGitHub Token 🚀 Quick Install系统依赖pip安装Linux, macOS, Windows (WSL)Windows (Powershell) 🚩 Roadmap🌏 项目交流讨论…...

修复 ChatGPT 发生错误的问题
目录 ChatGPT 发生错误?请参阅如何修复连接错误! 修复 ChatGPT 发生错误的问题 基本故障排除技巧 检查 ChatGPT 的服务器状态 检查 API 限制 检查输入格式 清除浏览数据 香港DSE是什么? 台湾指考是什么? 王湘浩 生平 …...
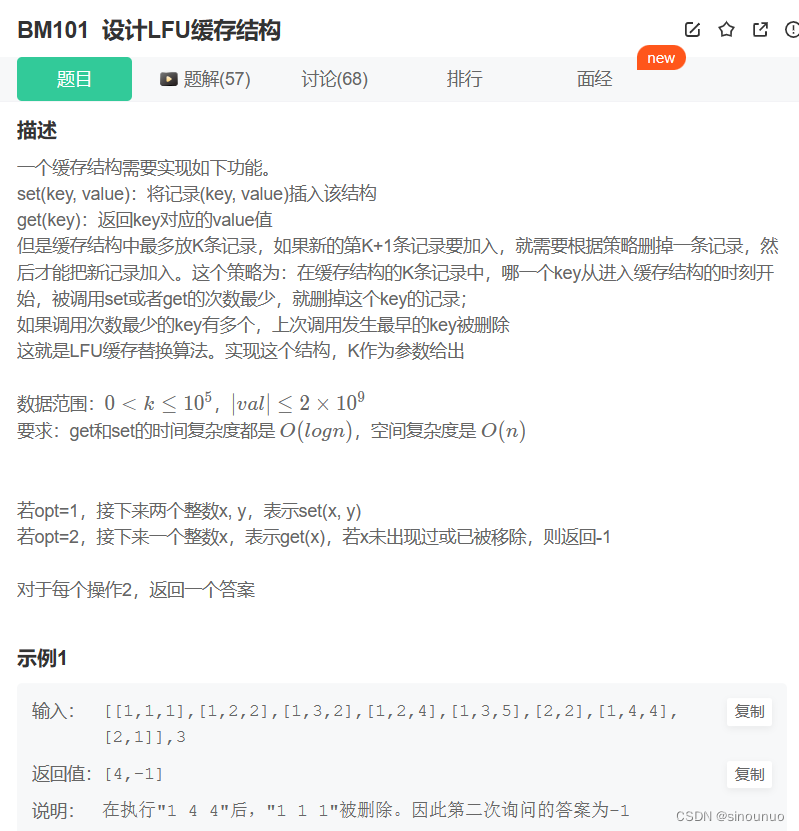
《热题100》字符串、双指针、贪心算法篇
思路:对于输入的的字符串,只有三种可能,ipv4,ipv6,和neither ipv4:四位,十进制,无前导0,小于256 ipv6:八位,十六进制,无多余0(00情况不允许),不…...

大数据组件Sqoop-安装与验证
🥇🥇【大数据学习记录篇】-持续更新中~🥇🥇 个人主页:beixi 本文章收录于专栏(点击传送):【大数据学习】 💓💓持续更新中,感谢各位前辈朋友们支持…...

运算符重载(个人学习笔记黑马学习)
1、加号运算符重载 #include <iostream> using namespace std; #include <string>//加号运算符重载 class Person { public://1、成员函数重载号//Person operator(Person& p) {// Person temp;// temp.m_A this->m_A p.m_A;// temp.m_B this->m_B p…...
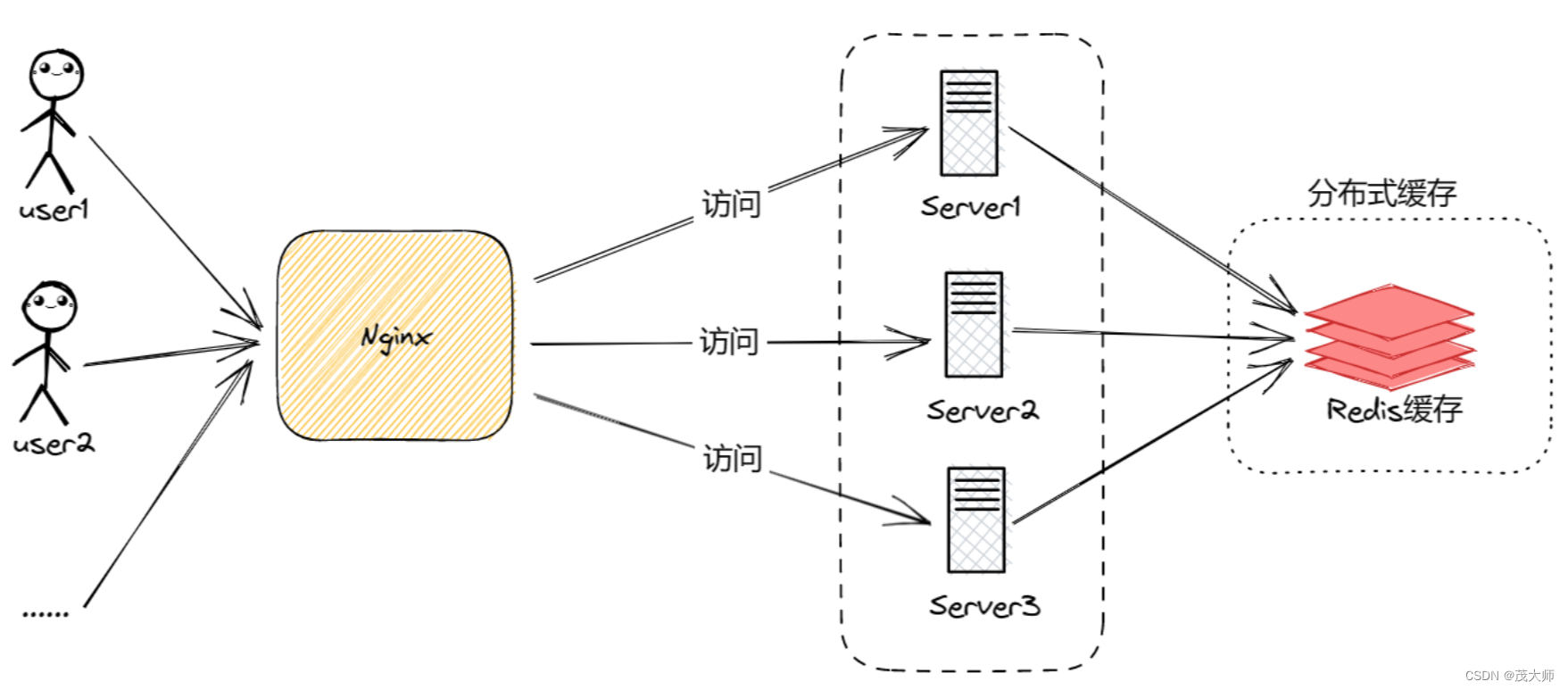
2023.9.6 Redis 的基本介绍
目录 Redis 的介绍 Redis 用作缓存和存储 session 信息 Redis 用作数据库 消息队列 消息队列是什么? Redis 用作消息队列 Redis 的介绍 特点: 内存中存储数据:奠定了 Redis 进行访问和存储时的快可编程性:支持使用 Lua 编写脚…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
