算法通关村第十九关——动态规划高频问题(白银)
算法通关村第十九关——动态规划高频问题(白银)
- 前言
- 1 最少硬币数
- 2 最长连续递增子序列
- 3 最长递增子序列
- 4 完全平方数
- 5 跳跃游戏
- 6 解码方法
- 7 不同路径 II
前言
摘自:代码随想录
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
- 确定递推公式
- 初始化dp数组
- 确定遍历顺序
- 举例推导dp数组
1 最少硬币数
leetcode 322. 零钱兑换
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[j]:凑足总额为 j 所需钱币的最少个数为dp[j]
- 确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],
那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
int[] dp = new int[amount + 1];
// 往数组dp里面填充某个数,这里选择amount+1,就是最大的值
Arrays.fill(dp, amount+1);
dp[0] = 0;
- 确定遍历顺序
有两种方式:
第一种:外循环遍历金额,内循环遍历硬币面额。
第二种:外循环遍历硬币面面额,内循环遍历金额。
这两种遍历顺序对应的意义如下:
-
外循环遍历金额,内循环遍历硬币面额:
这种遍历顺序的意义是在计算找零过程中,我们首先考虑金额的变化,然后再考虑不同的硬币面额。
也就是说,我们固定一个金额,尝试使用不同的硬币面额来找零。这样做的好处是可以利用之前已经计算出来的金额的最少硬币数,快速得到当前金额的最优解。由于金额是从小到大递增的,所以我们在计算每个金额的最优解时,可以利用前面较小金额的最优解已经被计算出来的特点。
// 遍历金额
for (int i = 1; i <= amount; i++) {// 遍历硬币面额for (int j = 0; j < coins.length; j++) {if (coins[j] <= i) {dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);}}
}
-
外循环遍历硬币面额,内循环遍历金额:
这种遍历顺序的意义是在计算找零过程中,我们首先考虑不同的硬币面额,然后再考虑不同的金额。
也就是说,我们固定一个硬币面额,尝试在不同的金额下进行找零。这样做的好处是可以保证我们将所有可能的硬币面额都考虑到,并且在计算每个金额的最优解时,可以利用之前已经计算出来的较小金额的最优解。由于硬币面额是从小到大递增的,所以我们在计算每个金额的最优解时,可以利用之前较小硬币面额的最优解已经被计算出来的特点。
// 遍历硬币面额
for (int coin : coins){// 遍历金额for (int i = 1; i <= amount; i++) {if(coin <= i){dp[i] = Math.min(dp[i], dp[i - coin] + 1);}}
}
全部代码如下:
第一种:
class Solution {public int coinChange(int[] coins, int amount) {// 初始化dp数组int[] dp = new int[amount + 1];Arrays.fill(dp, amount + 1);dp[0] = 0;// 遍历金额for (int i=1; i <= amount; i++) {// 遍历硬币面额for (int j=0; j < coins.length; j++){if(coins[j] <= i){dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);}}}return dp[amount] > amount ? -1 : dp[amount];}
}
第二种:
class Solution {public int coinChange(int[] coins, int amount) {// 初始化dp数组int[] dp = new int[amount + 1];Arrays.fill(dp, amount + 1);dp[0] = 0;// 遍历硬币面额for (int coin : coins){// 遍历金额for (int i = 1; i <= amount; i++) {if(coin <= i){dp[i] = Math.min(dp[i], dp[i - coin] + 1);}}}return dp[amount] > amount ? -1 : dp[amount];}
}
2 最长连续递增子序列
leetcode 674. 最长连续递增序列
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp数组:表示以当前元素为结尾的最长连续递增序列的长度。
dp[i]表示以nums[i]为结尾的最长连续递增序列的长度。
- 确定递推公式
如果nums[i] > nums[i-1],则dp[i] = dp[i-1] + 1;否则dp[i] = 1。
- dp数组如何初始化
我们将dp数组的所有元素初始化为1,因为每个元素都可以作为一个单独的递增序列。
- 确定遍历顺序
从第二个元素开始遍历:
for(int i=0; i < nums.length; i++){if(i > 0 && nums[i] > nums[i-1]){dp[i] = dp[i-1] + 1;}else{dp[i] = 1;}
}
- 举例说明
举例说明:给定数组nums = [1, 3, 5, 4, 7]。
遍历过程如下:
- 对于nums[1] = 3,nums[0] = 1 < nums[1],所以dp[1] = dp[0] + 1 = 2。
- 对于nums[2] = 5,nums[1] = 3 < nums[2],所以dp[2] = dp[1] + 1 = 3。
- 对于nums[3] = 4,nums[2] = 5 > nums[3],所以dp[3] = 1。
- 对于nums[4] = 7,nums[3] = 4 < nums[4],所以dp[4] = dp[3] + 1 = 2。
最终的最长连续递增序列的长度为dp数组的最大值,即为3。
最后代码如下:
class Solution {public int findLengthOfLCIS(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int[] dp = new int[nums.length];dp[0] = 1;for(int i=1; i < nums.length; i++){if(nums[i] > nums[i-1]){dp[i] = dp[i-1] + 1;}else{dp[i] = 1;}}return Arrays.stream(dp).max().getAsInt();}
}
不是使用stream的方式:
class Solution {public int findLengthOfLCIS(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int[] dp = new int[nums.length];dp[0] = 1;int maxLength = 1;for(int i=1; i < nums.length; i++){if(nums[i] > nums[i-1]){dp[i] = dp[i-1] + 1;}else{dp[i] = 1;}maxLength = Math.max(maxLength, dp[i]);}return maxLength;}
}
还可以得到dp[i],再遍历一遍得到最大值,这就不写了
3 最长递增子序列
leetcode 300. 最长递增子序列
-
确定dp数组(dp table)及其下标的含义:
- dp数组:dp[i] 表示以第i个数字结尾的最长递增子序列的长度。
- 下标的含义:dp[i] 表示以第i个数字结尾的最长递增子序列的长度。
-
确定递推公式:
- 如果nums[i] > nums[j],则:dp[i] = max(dp[i], dp[j] + 1)。
为啥呢??
这里的i和j表示数组
nums的索引。具体来说,i表示当前遍历到的元素的索引,而j表示在i之前的元素的索引。当我们遍历到第i个元素时,我们需要寻找在i之前的元素中比nums[i]小的元素。这样,我们就可以利用这个小于nums[i]的元素来构成一个更长的递增子序列。
所以,当nums[i] > nums[j]时,表示nums[i]比nums[j]大,我们可以将以j结尾的最长递增子序列的长度加1,然后与以i结尾的最长递增子序列的长度进行比较,取较大的值作为以i结尾的最长递增子序列的长度。也就是递推公式中的
dp[i] = max(dp[i], dp[j] + 1)。 -
初始化dp数组:
- 初始时,dp数组中的每个元素都设为1,因为最短的递增子序列长度为1。
-
确定遍历顺序:
- 外层循环遍历数组nums,从左到右依次计算dp[i]的值。
- 内层循环遍历数组nums,从数组开始到i的位置,寻找前面的数字nums[j]是否小于nums[i],如果是,则根据递推公式更新dp[i]的值。
-
举例推导dp数组:
如果nums[i] > nums[j],则dp[i] = max(dp[i], dp[j] + 1)。
逐个元素计算dp[i]的值:
- 当i = 1时,nums[i] = 9,此时没有比9小的元素,所以以9结尾的最长递增子序列长度仍为1。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 1 1 1 1 1- 当i = 2时,nums[i] = 2,此时在2之前有9和10两个元素,都比2大,所以以2结尾的最长递增子序列长度仍为1。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 1 1 1 1 1- 当i = 3时,nums[i] = 5,此时在5之前有2和9两个元素,其中2比5小,所以以5结尾的最长递增子序列长度为dp[2] + 1 = 2。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 2 1 1 1 1- 当i = 4时,nums[i] = 3,此时在3之前有2和5两个元素,其中2比3小,所以以3结尾的最长递增子序列长度为dp[2] + 1 = 2。
nums: 10 9 2 5 3 7 101 18
dp: 1 1 1 2 2 1 1 1
后面略~~~~~~
完整代码如下:
class Solution {public int lengthOfLIS(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int n = nums.length;int[] dp = new int[n];dp[0] = 1; int result = 1; for (int i = 1; i < n; i++) {dp[i] = 1; for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) { dp[i] = Math.max(dp[i], dp[j] + 1); }}result = Math.max(result, dp[i]); }return result;}
}
4 完全平方数
leetcode 279. 完全平方数
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
**dp[i]:**表示数字i的最少完全平方数的个数。
- 确定递推公式
对于数字 i 来说,我们需要遍历所有小于等于 i 的完全平方数 j( j 从 1 到 sqrt(i) ),然后将当前数字 i 减去 j 得到差值,即 i - j 。我们需要找到 dp[ i - j * j ] 的最小值,然后再加上1(表示当前完全平方数 j ),即可得到dp[i]的值。
递推公式为:dp[i] = Math.min(dp[i], dp[i - j * j] + 1),其中 j * j <= i。
- 初始化dp数组
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
- 确定遍历顺序
// 遍历dp数组
for (int i = 1; i <= n; i++) {// 遍历小于等于i的完全平方数j*jfor (int j = 1; j * j <= i; j++) {// 更新dp[i]dp[i] = Math.min(dp[i], dp[i - j * j] + 1);}
}
- 举例推导dp数组
略。。。
完整代码:
class Solution {public int numSquares(int n) {// 定义dp数组int[] dp = new int[n + 1];// 初始化dp数组Arrays.fill(dp, n+1);dp[0] = 0;// 遍历dp数组for (int i = 1; i <= n; i++) {// 遍历小于等于i的完全平方数j*jfor (int j = 1; j * j <= i; j++) {// 更新dp[i]dp[i] = Math.min(dp[i], dp[i - j * j] + 1);}}return dp[n]; }
}
当然,这个代码可以再优化一下:(使用Math的api)
减少内层循环的次数:对于小于等于 i 的完全平方数 j ,我们可以通过计算 i - j * j 的平方根得到 j 的最大值,并从最大值开始遍历,这样可以减少内层循环的次数。
class Solution {public static int numSquares(int n) {// 定义dp数组int[] dp = new int[n + 1];// 初始化dp数组Arrays.fill(dp, n + 1);dp[0] = 0;// 遍历dp数组for (int i = 1; i <= n; i++) {// 获取当前数字i的最大完全平方数j*jint maxSquare = (int) Math.sqrt(i);// 遍历完全平方数j*jfor (int j = maxSquare; j >= 1; j--) {// 更新dp[i]dp[i] = Math.min(dp[i], dp[i - j * j] + 1);}}return dp[n];}
}
5 跳跃游戏
leetcode 55. 跳跃游戏
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
dp[i]表示从起点位置到达位置i时能否跳跃到最后一个位置。
- 确定递推公式
dp[i] = (dp[j] && nums[j] >= i - j),其中0 <= j < i
- 初始化dp数组
初始化dp数组所有位置为false。
- 确定遍历顺序
外层循环遍历i从1到n-1,内层循环遍历j从0到i-1。
- 举例推导dp数组
以数组nums = [2, 3, 1, 1, 4]为例进行推导:
初始状态:
dp = [false, false, false, false, false]
推导dp[1]:
dp[1] = (dp[0] && nums[0] >= 1 - 0) = (false && 2 >= 1) = false
推导dp[2]:
dp[2] = (dp[0] && nums[0] >= 2 - 0) || (dp[1] && nums[1] >= 2 - 1) = (false && 2 >= 2) || (false && 3 >= 2) = false
推导dp[3]:
dp[3] = (dp[0] && nums[0] >= 3 - 0) || (dp[1] && nums[1] >= 3 - 1) || (dp[2] && nums[2] >= 3 - 2) = (false && 2 >= 3) || (false && 3 >= 3) || (false && 1 >= 3) = false
完整代码如下:
class Solution {public boolean canJump(int[] nums) {// 获取数组长度int n = nums.length;// 定义dp数组boolean[] dp = new boolean[n];// 初始化dp数组dp[0] = true;// 遍历dp数组for (int i = 1; i < n; i++) {// 内层循环遍历jfor (int j = 0; j < i; j++) {// 更新dp[i]dp[i] = dp[j] && nums[j] >= i - j;// 如果dp[i]为true,则跳出内层循环if (dp[i]) {break;}}}return dp[n - 1];}
}
6 解码方法
leetcode 91. 解码方法
动态规划五部曲:
- 确定dp数组(dp table)及其下标的含义
dp[i]表示从字符串的起始位置到第i个字符时的解码方法总数。
- 确定递推公式
对于dp数组中的每个位置i,我们需要考虑两个情况:
- 如果第i个字符能够单独解码(即不为0),则dp[i] = dp[i-1],因为第i个字符自身可以作为一个解码方法;
- 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间),则dp[i] += dp[i-2],因为组成的两位数可以作为一个解码方法。
则,递推公式为:dp[i] = dp[i-1] + dp[i-2],其中0 <= i < n。
- 初始化dp数组
初始化dp数组的长度为n+1,初始值为0。
- 确定遍历顺序
for (int i = 1; i <= n; i++) {// 如果第i个字符能够单独解码(即不为0)if (s.charAt(i - 1) != '0') {dp[i] += dp[i - 1];}// 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间)if (i >= 2 && isValidEncoding(s.substring(i - 2, i))) {dp[i] += dp[i - 2];}
}
// 判断字符串编码是否在1到26之间
private static boolean isValidEncoding(String s) {if (s.charAt(0) == '0') {return false;}int num = Integer.parseInt(s);return num >= 1 && num <= 26;
}
- 举例推导dp数组
以字符串s = "226"为例进行推导:
初始状态:
dp = [1, 0, 0, 0]
推导dp[1]:
如果第1个字符为2,能够单独解码为"2",所以dp[1] = dp[0] = 1
推导dp[2]:
如果第2个字符为2,能够单独解码为"2",所以dp[2] = dp[1] = 1
如果第1个字符与第2个字符组成的两位数为26,能够解码为"26",所以dp[2] += dp[0],即dp[2] = dp[1] + dp[0] = 1 + 1 = 2
推导dp[3]:
如果第3个字符为6,能够单独解码为"6",所以dp[3] = dp[2] = 2
如果第2个字符与第3个字符组成的两位数为26,能够解码为"26",所以dp[3] += dp[1],即dp[3] = dp[2] + dp[1] = 2 + 1 = 3
最终结果:
dp = [1, 1, 2, 3]
完整代码:
class Solution {public static int numDecodings(String s) {// 获取字符串的长度int n = s.length();// 定义dp数组int[] dp = new int[n + 1];// 初始化dp数组dp[0] = 1;// 遍历dp数组for (int i = 1; i <= n; i++) {// 如果第i个字符能够单独解码(即不为0)if (s.charAt(i - 1) != '0') {dp[i] += dp[i - 1];}// 如果第i个字符与前一个字符组成的两位数能够解码(即与前一个字符组成的数字在1到26之间)if (i >= 2 && isValidEncoding(s.substring(i - 2, i))) {dp[i] += dp[i - 2];}}return dp[n];}// 判断字符串编码是否在1到26之间private static boolean isValidEncoding(String s) {if (s.charAt(0) == '0') {return false;}int num = Integer.parseInt(s);return num >= 1 && num <= 26;}
}
不过可以简化一下,就是比较难理解一点,意义一样滴:
class Solution {public int numDecodings(String s) {int n = s.length();int[] f = new int[n + 1];f[0] = 1;for (int i = 1; i <= n; ++i) {if (s.charAt(i - 1) != '0') {f[i] += f[i - 1];}if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {f[i] += f[i - 2];}}return f[n];}
}
7 不同路径 II
leetcode 63. 不同路径 II
这题就是62的改版,所以复杂了很多,还是建议看代码随想录:动态规划——不同路径
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
**dp[i] [j] :**表示从(0 ,0)出发,到(i, j) 有dp[i] [j]条不同的路径。
- 确定递推公式
递推公式和62.不同路径一样,dp[i] [j] = dp[i - 1] [j] + dp[i] [j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
所以代码为:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
- dp数组如何初始化
因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i] [0]一定为1,dp[0] [j]也同理。
但如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i] [0]应该还是初始值0。
如图:
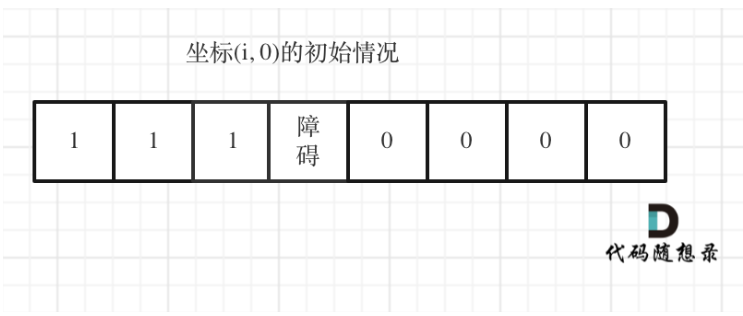
下标(0, j)的初始化情况同理。
所以本题初始化代码为:
int[][] dp = new int[m][n];
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;
}
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i] [0] == 1的情况就停止dp[i] [0]的赋值1的操作,dp[0] [j]同理
- 确定遍历顺序
从递归公式dp[i] [j] = dp [i - 1] [j] + dp[i] [j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i] [j]的时候,dp[i - 1] [j] 和 dp[i] [j - 1]一定是有数值。
代码如下:
for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;}
}
- 举例推导dp数组
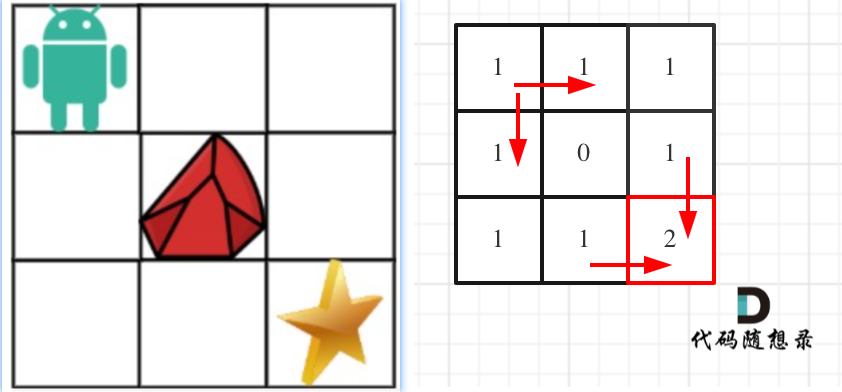
完整代码如下:
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m][n];//如果在起点或终点出现了障碍,直接返回0if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {return 0;}for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;}for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;}}return dp[m - 1][n - 1];}
}
至于118,119我个人觉得并不合适使用动态规划的方式,所以就不写了,over~~
相关文章:

算法通关村第十九关——动态规划高频问题(白银)
算法通关村第十九关——动态规划高频问题(白银) 前言1 最少硬币数2 最长连续递增子序列3 最长递增子序列4 完全平方数5 跳跃游戏6 解码方法7 不同路径 II 前言 摘自:代码随想录 动态规划五部曲: 确定dp数组(dp tabl…...
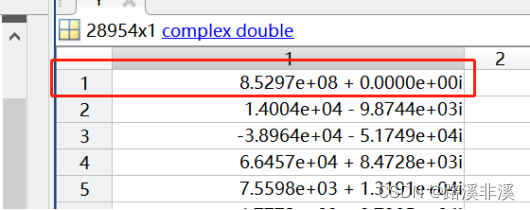
Matlab如何导入Excel数据并进行FFT变换
如果你发现某段信号里面有干扰,想要分析这段信号里面的频率成分,就可以使用matlab导入Excel数据后进行快速傅里叶变换(fft)。 先直接上使用方法,后面再补充理论知识。 可以通过串口将需要分析的数据发送到串口助手&a…...
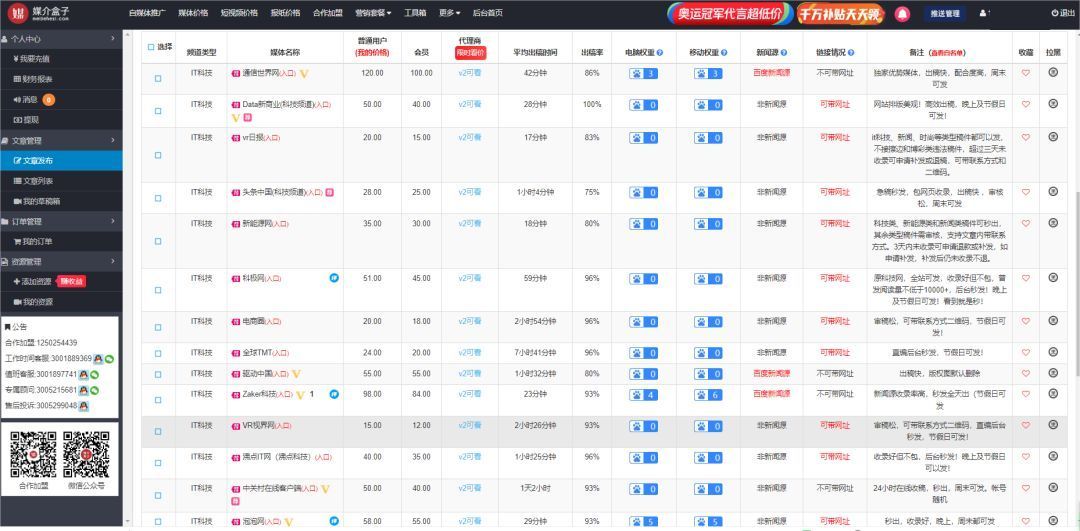
华为mate60 上线 媒介盒子多家媒体报道
为什么你的品牌营销不见效?如何能推动品牌破圈?让媒介盒子给你一些启发。本期盒子要跟大家分享地新机上市,数码科技行业企业该如何做线上宣传。 HUAWEI Mate 60系列8月29日官宣发布,出色的拍照功能、强大的性能表现和持久的续航能…...

Java知识总结(持续更新)
一、JDK、JRE、JVM三者之间的关系? 1. **JDK (Java Development Kit)**: JDK 是 Java 开发工具包,它包含了用于开发 Java 应用程序的所有必要工具和库。这包括 Java 编译器(javac)、Java 核心类库、开发工具&#x…...

缓存技术:加速应用,提高用户体验
本文总结前期某个系统中使用到的缓存使用经验—仅此而已,效果还不错。 缓存技术在系统架构设计中扮演着至关重要的角色,它不仅可以显著提高系统的性能,还可以改善用户体验。在本文章中,我们将探讨不同类型的缓存、缓存失效以及缓存淘汰等关键概念,帮助在后期的架构设计中…...

MySQL中分区与分表的区别
MySQL中分区与分表的区别 一、分区与分表的区别 分区和分表是在处理大规模数据时的两种技术手段,尽管它们的目标都是提升系统的性能和数据管理的效率,但它们的实现方式和应用场景略有不同。 1. 分区 分区是将一个大表分割为多个更小的子表,…...
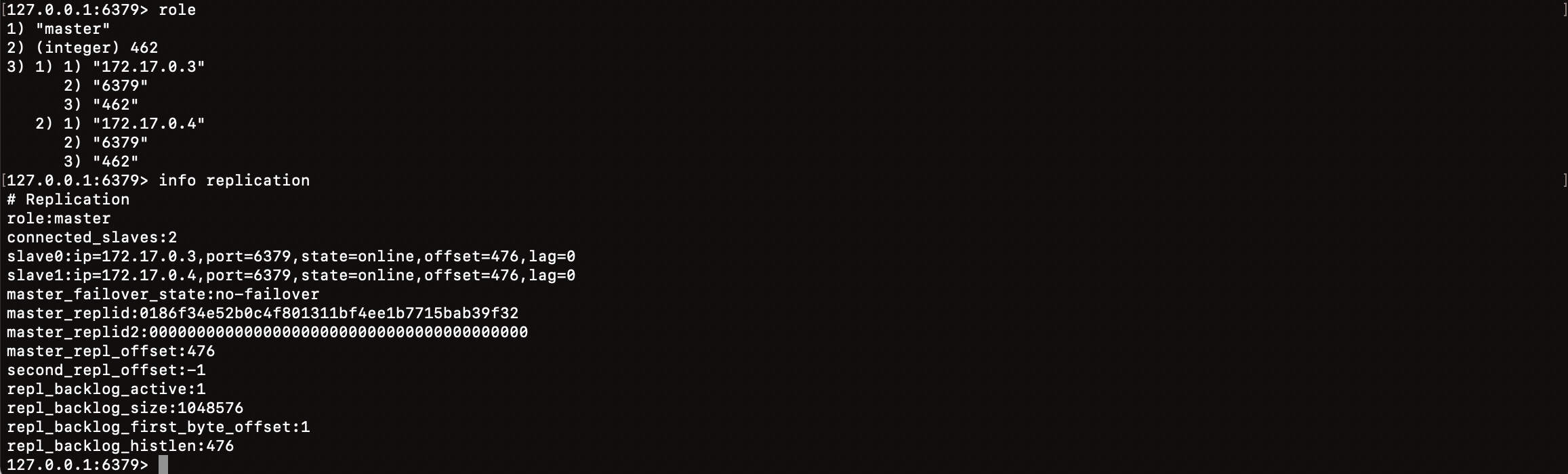
Redis主从复制集群的介绍及搭建
在现代的软件开发中,数据的可靠性和可用性是至关重要的。Redis,作为一个开源的、内存中的数据结构存储系统,以其出色的性能和灵活的数据结构,赢得了开发者们的广泛喜爱。而 Redis 的主从复制功能,更是为我们提供了一种…...

MAC M1芯片安装mounty读写移动硬盘中的文件
因为移动硬盘中的文件是微软公司NTFS格式,MAC只支持自己的APFS或者HFS,与微软的NTFS不兼容,所以需要第三方的软件来支持读写硬盘中的文件,经过一上午的折腾,最终选择安装mounty这个免费的第三方软件 工具网址连接&am…...

原生Js Canvas去除视频绿幕背景
Js去除视频背景 注: 这里的去除视频背景并不是对视频文件进行操作去除背景 如果需要对视频扣除背景并导出可以使用ffmpeg等库,这里仅作播放用所以采用这种方法 由于uniapp中的canvas经过封装,且 uniapp 的 drawImage 无法绘制视频帧画面&…...
每天10个小知识点)
Vue知识系列(1)每天10个小知识点
目录 系列文章目录知识点**1. Vue修饰符**的概念、作用、原理、特性、优点、缺点、区别、使用场景**2. 双向数据绑定**的概念、作用、原理、特性、优点、缺点、区别、使用场景**3. MVVM、MVC、MVP** 的概念、作用、原理、特性、优点、缺点、区别、使用场景**4. slot** 的概念、…...
聚合基本使用)
Elasticsearch(三)聚合基本使用
基础概念 bucket 数据分组,一些数据按照某个字段进行bucket划分,这个字段值相同的数据放到一个bucket中。可以理解成Java中的Map<String, List>结构,类似于Mysql中的group by后的查询结果。 metric: 对一个数据分组执行…...

单片机C语言实例:14、音频输出
一、喇叭发声原理 程序实例1: #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存器的定义sbit SPK P1^2; //定义喇叭端口 /*------------------------------------------------函数声明 --------------…...

docker 和 podman的区别
Podman 和 Docker 都是用于容器化应用程序的工具,它们在很多方面非常相似,但也有一些关键区别: 1. 架构和权限: - Docker:Docker 使用守护进程(dockerd)来管理容器,它需要在操作…...
苹果手机远程控制安卓手机,为什么不能发起控制?
这位用户想要用iOS设备远程控制安卓设备,在被控端安装好AirDroid之后,就在控制端的苹果手机上也安装了AirDroid,然而打开控制端的软件,却没有在手机界面上看到【远程控制】按钮,于是提出了以上疑问。 解答 想要让iOS设…...

Gradle 配置国内镜像
我们在使用gradle构建项目的时候,每当需要build或者刷新依赖的时候,由于gradle需要从服务器下载各种依赖包,速度非常慢,根本原因是由于gradle服务器在国外,而国内有些一些大厂和高校(比如阿里,华为…...

Spring AOP使用指南: 强大的面向切面编程技术
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Spring Boot集成Elasticsearch实战
文章目录 一、简介二、安装与配置Elasticsearch三、集成Spring Boot与Elasticsearch1. 添加依赖与配置文件2. 创建Elasticsearch数据模型3. 定义Elasticsearch仓库接口4. 实现Elasticsearch数据操作 四、基本查询与索引操作1. 插入与更新数据2. 删除数据与索引3. 条件查询与分页…...

【python零基础入门学习】python基础篇之文件对象open、模块以及函数的使用(三)
本站以分享各种运维经验和运维所需要的技能为主 《python》:python零基础入门学习 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8》暂未更新 《docker学习》暂未更新 《ceph学习》ceph日常问题解…...
【JavaEE】_CSS常用属性值
目录 1. 字体属性 1.1 设置字体家族 font-family 1.2 设置字体大小 font-size 1.3 设置字体粗细 font-weight 1.4 设置字体倾斜 font-style 2. 文本属性 2.1 设置文本颜色 color 2.2 文本对齐 text-align 2.3 文本装饰 text-decoration 2.4 文本缩进 text-indent 2.…...
vue组件库开发,webpack打包,发布npm
做一个像elment-ui一样的vue组件库 那多好啊!这是我前几年就想做的 但webpack真的太难用,也许是我功力不够 今天看到一个视频,早上6-13点,终于实现了,呜呜 感谢视频的分享-来龙去脉-大家可以看这个视频:htt…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
