【图论】SPFA求负环
算法提高课笔记
文章目录
- 基础知识
- 例题
- 虫洞
- 题意
- 思路
- 代码
- 观光奶牛
- 题意
- 思路
- 代码
- 单词环
- 题意
- 思路
- 代码
基础知识
负环:环上权值之和是负数
求负环的常用方法 基于SPFA
- 统计每个点入队次数,如果某个点入队n次,则说明存在负环(完全等价于Bellman-Ford算法)
- 统计当前每个点的最短路中所包含的边数,如果某点的最短路包含的边数大于等于n,则说明存在负环
玄学结论:当所有点的入队次数超过2n时,就认为图中有很大肯存在负环
例题
虫洞
原题链接
农夫约翰在巡视他的众多农场时,发现了很多令人惊叹的虫洞。
虫洞非常奇特,它可以看作是一条 单向 路径,通过它可以使你回到过去的某个时刻(相对于你进入虫洞之前)。
农夫约翰的每个农场中包含 N 片田地,M 条路径(双向)以及 W 个虫洞。
现在农夫约翰希望能够从农场中的某片田地出发,经过一些路径和虫洞回到过去,并在他的出发时刻之前赶到他的出发地。
他希望能够看到出发之前的自己。
请你判断一下约翰能否做到这一点。
下面我们将给你提供约翰拥有的农场数量 F,以及每个农场的完整信息。
已知走过任何一条路径所花费的时间都不超过 10000 秒,任何虫洞将他带回的时间都不会超过 10000 秒。
输入格式
第一行包含整数 F,表示约翰共有 F 个农场。
对于每个农场,第一行包含三个整数 N,M,W。
接下来 M 行,每行包含三个整数 S,E,T,表示田地 S 和 E 之间存在一条路径,经过这条路径所花的时间为 T。
再接下来 W 行,每行包含三个整数 S,E,T,表示存在一条从田地 S 走到田地 E 的虫洞,走过这条虫洞,可以回到 T 秒之前。
输出格式
输出共 F行,每行输出一个结果。
如果约翰能够在出发时刻之前回到出发地,则输出 YES,否则输出 NO。
数据范围
1 ≤ F ≤ 5 1≤F≤5 1≤F≤5
1 ≤ N ≤ 500 , 1≤N≤500, 1≤N≤500,
1 ≤ M ≤ 2500 , 1≤M≤2500, 1≤M≤2500,
1 ≤ W ≤ 200 , 1≤W≤200, 1≤W≤200,
1 ≤ T ≤ 10000 , 1≤T≤10000, 1≤T≤10000,
1 ≤ S , E ≤ N 1≤S,E≤N 1≤S,E≤N
输入样例
2
3 3 1
1 2 2
1 3 4
2 3 1
3 1 3
3 2 1
1 2 3
2 3 4
3 1 8
输出样例
NO
YES
题意
负环板题
思路
跑一遍spfa
代码
#include <bits/stdc++.h>using namespace std;const int N = 510, M = 5210;int n, m1, m2;
int h[N], ne[M], e[M], w[M], idx;
int dist[N];
int cnt[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}bool spfa()
{memset(dist, 0, sizeof dist);memset(cnt, 0, sizeof cnt);memset(st, 0, sizeof st);queue<int> q;for (int i = 1; i <= n; i ++ ){q.push(i);st[i] = true;}while (q.size()){int t = q.front();q.pop();st[t] = false;for (int i = h[t]; ~i; i = ne[i]){int j = e[i];if (dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];cnt[j] = cnt[t] + 1;if (cnt[j] >= n) return true; // 更新次数一旦超过n就说明有负环if (!st[j]){q.push(j);st[j] = true;}}}}return false;
}int main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int T;cin >> T;while (T -- ){cin >> n >> m1 >> m2;memset(h, -1, sizeof h);idx = 0;for (int i = 0; i < m1; i ++ ){int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c);}for (int i = 0; i < m2; i ++ ){int a, b, c;cin >> a >> b >> c;add(a, b, -c);}if (spfa()) puts("YES");else puts("NO");}
}
观光奶牛
原题链接
给定一张 L 个点、P 条边的有向图,每个点都有一个权值 f[i],每条边都有一个权值 t[i]。
求图中的一个环,使“环上各点的权值之和”除以“环上各边的权值之和”最大。
输出这个最大值。
注意:数据保证至少存在一个环。
输入格式
第一行包含两个整数 L 和 P。
接下来 L 行每行一个整数,表示 f[i]。
再接下来 P 行,每行三个整数 a,b,t[i],表示点 a 和 b 之间存在一条边,边的权值为 t[i]。
输出格式
输出一个数表示结果,保留两位小数。
数据范围
2 ≤ L ≤ 1000 , 2≤L≤1000, 2≤L≤1000,
2 ≤ P ≤ 5000 , 2≤P≤5000, 2≤P≤5000,
1 ≤ f [ i ] , t [ i ] ≤ 1000 1≤f[i],t[i]≤1000 1≤f[i],t[i]≤1000
输入样例
5 7
30
10
10
5
10
1 2 3
2 3 2
3 4 5
3 5 2
4 5 5
5 1 3
5 2 2
输出样例
6.00
题意
给出点权和边权,求一个环使得点权之和除以边权之和最大
思路
求比值最大的问题 -> 01分数规划 -> 二分
首先确定边界值,答案一定在[0, 1000) 之间
每次取中点mid,如果图中存在一个环使得比值大于mid,则答案在mid和r之间,反之亦然
现在问题变成了如何判断是否存在一个比值大于mid的环?
判断: ∑ f i ∑ t i > M i d \frac{\sum f_i}{\sum t_i}>Mid ∑ti∑fi>Mid
化简: ∑ f i − M i d ∗ ∑ t i > 0 \sum f_i-Mid*\sum t_i>0 ∑fi−Mid∗∑ti>0
在环上的点权我们可以任意加到边权上,对环不会有影响,假设我们将所有点权加到出边上,化简: ∑ ( f i − M i d ∗ t i ) > 0 \sum (f_i-Mid*t_i)>0 ∑(fi−Mid∗ti)>0
现在将边权全看成 f i − M i d ∗ t i f_i-Mid*t_i fi−Mid∗ti
问题转换成了:图中是否存在一个正环
求最长路即可
代码
#include <bits/stdc++.h>using namespace std;const int N = 1010, M = 5010;int n, m;
int wf[N];
int h[N], e[M], ne[M], wt[M], idx;
double dist[N];
int cnt[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, wt[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}bool check(double mid)
{memset(dist, 0, sizeof dist);memset(st, 0, sizeof st);memset(cnt, 0, sizeof cnt);queue<int> q;for (int i = 1; i <= n; i ++ ) // 所有点存进队列{q.push(i);st[i] = true;}while (q.size()){int t = q.front();q.pop();st[t] = false;for (int i = h[t]; ~i; i = ne[i]){int j = e[i];if (dist[j] < dist[t] + wf[t] - mid * wt[i]){dist[j] = dist[t] + wf[t] - mid * wt[i]; // 更新最长距离cnt[j] = cnt[t] + 1;if (cnt[j] >= n) return true; // 更新次数超过n就说明有正环if (!st[j]){q.push(j);st[j] = true;}}}}return false;
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ) cin >> wf[i]; // 记录点权memset(h, -1, sizeof h);for (int j = 0; j < m; j ++ ){int a, b, c;cin >> a >> b >> c;add(a, b, c);}double l = 0, r = 1e6;while (r - l > 1e-4) // 误差{double mid = (l + r) / 2;if (check(mid)) l = mid;else r = mid;}printf("%.2lf\n", l);
}
单词环
原题链接
我们有 n 个字符串,每个字符串都是由 a∼z 的小写英文字母组成的。
如果字符串 A 的结尾两个字符刚好与字符串 B 的开头两个字符相匹配,那么我们称 A 与 B 能够相连(注意:A 能与 B 相连不代表 B 能与 A 相连)。
我们希望从给定的字符串中找出一些,使得它们首尾相连形成一个环串(一个串首尾相连也算),我们想要使这个环串的平均长度最大。
如下例:
ababc
bckjaca
caahoynaab
第一个串能与第二个串相连,第二个串能与第三个串相连,第三个串能与第一个串相连,我们按照此顺序相连,便形成了一个环串,长度为 5+7+10=22(重复部分算两次),总共使用了 3 个串,所以平均长度是 223≈7.33。
输入格式
本题有多组数据。
每组数据的第一行,一个整数 n,表示字符串数量;
接下来 n 行,每行一个长度小于等于 1000 的字符串。
读入以 n=0 结束。
输出格式
若不存在环串,输出”No solution”,否则输出最长的环串的平均长度。
只要答案与标准答案的差不超过 0.01,就视为答案正确。
数据范围
1 ≤ n ≤ 105 1≤n≤105 1≤n≤105
输入样例
3
intercommunicational
alkylbenzenesulfonate
tetraiodophenolphthalein
0
输出样例
21.66
题意
n个字符串,如果a的末尾两个字符和b的开头相同则能相连,求能构成的环的平均长度最大值
思路
把每个字符串的首位两个字母看做一个点,比如说样例可以这样建图:

答案就变成了求 ∑ w i ∑ 1 \frac{\sum w_i}{\sum 1} ∑1∑wi的最大值
答案在(0, 1000)之内,二分做,类似观光奶牛
最终判断式为: ∑ w i − M i d ∗ ∑ 1 > 0 \sum w_i - Mid*\sum 1>0 ∑wi−Mid∗∑1>0
判断有没有解直接把 Mid = 0 代入即可,因为如果等于0都不能满足的话大于0就更不会满足了
于是成功TLE,用一下玄学优化
代码
#include <bits/stdc++.h>using namespace std;const int N = 700, M = 100010;int n;
int h[N], e[M], ne[M], w[M], idx;
double dist[N];
int cnt[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}bool check(double mid)
{memset(st, 0, sizeof st);memset(cnt, 0, sizeof cnt);queue<int> q;for (int i = 0; i < 676; i ++ ) // 所有点存入队列{q.push(i);st[i] = true;}int count = 0;while (q.size()){int t = q.front();q.pop();st[t] = false;for (int i = h[t]; ~i; i = ne[i]){int j = e[i];if (dist[j] < dist[t] + w[i] - mid){dist[j] = dist[t] + w[i] - mid;cnt[j] = cnt[t] + 1;if (++ count > 10000) return true; // 次数过多直接返回(玄学可能失败if (cnt[j] >= N) return true; // 这个是保证一定正确的if (!st[j]){q.push(j);st[j] = true;}}}}return false;
}int main()
{char str[1010];while (scanf("%d", &n), n){memset(h, -1, sizeof h);idx = 0;for (int i = 0; i < n; i ++ ){cin >> str;int len = strlen(str);if (len >= 2){// 用类似于26进制的方法存储int left = (str[0] - 'a') * 26 + str[1] - 'a';int right = (str[len - 2] - 'a') * 26 + str[len - 1] - 'a';add(left, right, len);}}if (!check(0)) puts("No solution"); // 判断是否有解else{double l = 0, r = 1000;while (r - l > 1e-4) // 误差{double mid = (l + r) / 2;if (check(mid)) l = mid;else r = mid;}printf("%lf\n", r);}}
}
相关文章:

【图论】SPFA求负环
算法提高课笔记 文章目录 基础知识例题虫洞题意思路代码 观光奶牛题意思路代码 单词环题意思路代码 基础知识 负环:环上权值之和是负数 求负环的常用方法 基于SPFA 统计每个点入队次数,如果某个点入队n次,则说明存在负环(完全…...
vue3中的吸顶导航交互实现 | VueUse插件
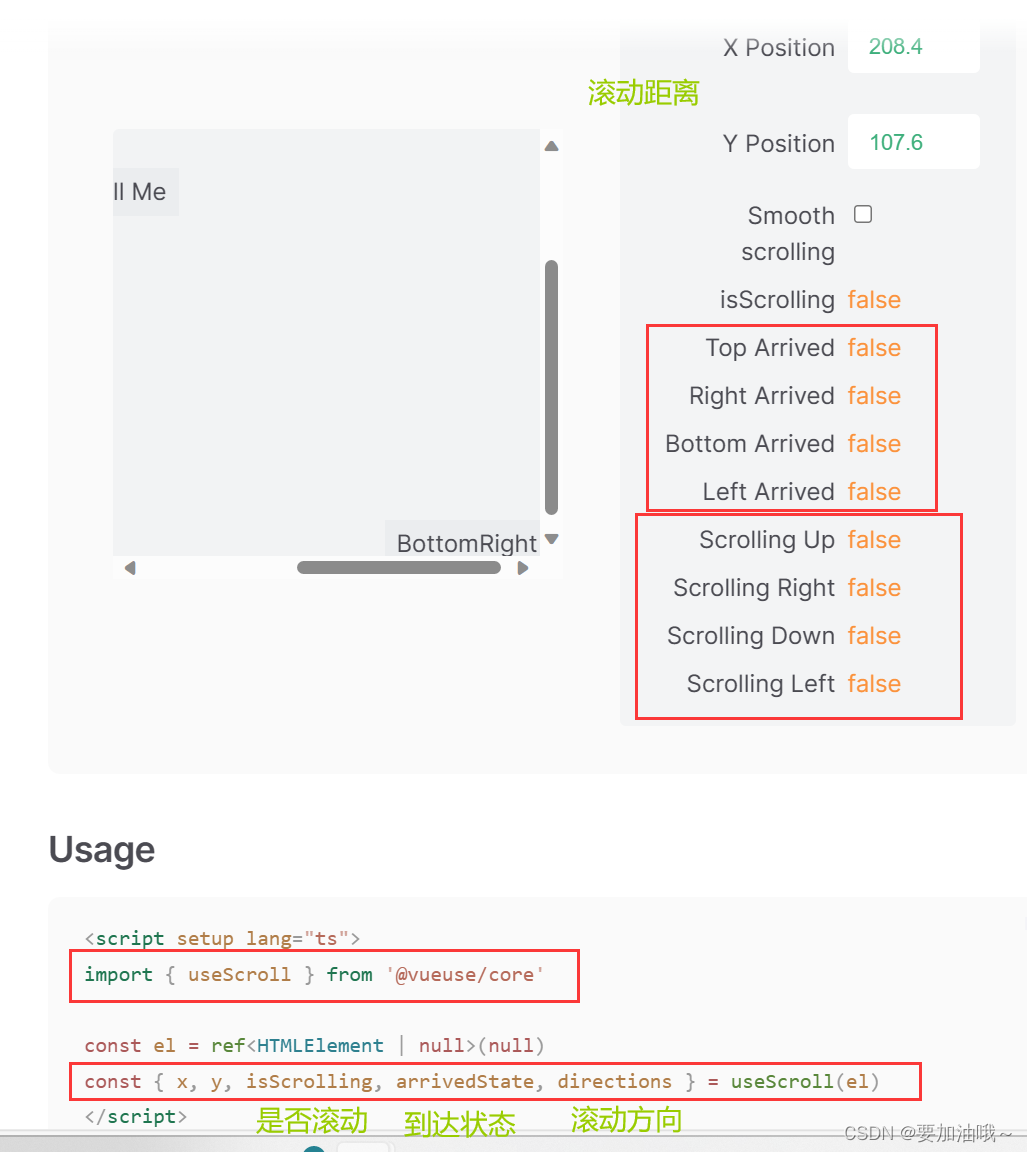
目的:浏览器上下滚动时,若距离顶部的滚动距离大于78px,吸顶导航显示,小于78px隐藏。使用vueuse插件中的useScroll方法和动态类名控制进行实现 1. 安装 npm i vueuse/core 2. 获得滚动距离 项目中导入࿰…...

MySql 笔记
数据结构:BTREE 二叉树:顺序增长依次查询效率低 红黑树: 数据多了深度越深,效率自然低了 HASH: 查询条件限制 B-TREE:度(degree)-节段的数据存储个数,叶节点具有 相…...
部署elasticsearch集群
创建es集群 编写一个docker-compose.yaml文件,内容如下 version: 2.2 services:es01:image: elasticsearch:7.12.1container_name: es01environment:- node.namees01- cluster.namees-docker-cluster- discovery.seed_hostses02,es03- cluster.initial_master_nod…...
)
CTF入门学习笔记——Crypto密码(现代密码)
文章目录 CTF入门学习笔记——Crypto密码(现代密码)因数分解因数分解 共享素数Bigrsa 低加密指数攻击(小明文攻击)crypto5 共模攻击rsa_output 广播攻击Crazy_Rsa_Tech 待补充 CTF入门学习笔记——Crypto密码(现代密码…...

(3)MyBatis-Plus待开发
常用注解 TableName MyBatis-Plus在确定操作的表时,由BaseMapper的泛型决定即实体类型决定,且默认操作的表名和实体类型的类名一致,如果不一致则会因找不到表报异常 //向表中插入一条数据 Test public void testInsert(){User user new User(null, &…...

正则表达式参考手册
修饰符 修饰符用于执行区分大小写和全局匹配: 修饰符描述i执行对大小写不敏感的匹配。g执行全局匹配(查找所有匹配而非在找到第一个匹配后停止)。m执行多行匹配。 方括号 方括号用于查找某个范围内的字符: 表达式描述[abc]查找方括号之间…...

【农业生产模拟】WOFOST模型与PCSE模型实践
查看原文>>>【农业生产模拟】WOFOST模型与PCSE模型实践 实现作物产量的准确估算对于农田生态系统响应全球变化、可持续发展、科学粮食政策制定、粮食安全维护都至关重要。传统的经验模型、光能利用率模型等估产模型原理简单,数据容易获取,但是…...

PHP8中获取并删除数组中最后一个元素-PHP8知识详解
在php8中,array_pop()函数将返回数组的最后一个元素,并且将该元素从数组中删除。语法格式如下: array_pop(目标数组) 获取并删除数组中最后一个元素,参考代码: <?php $stu array(s001>明明,s002>亮亮,s…...
)
JS原理-笔记(1/3)
JS原理-笔记(1/3) 知识点自测 今天课程中涉及到的已学习知识点 函数的call方法-文档链接 // 以指定的this调用函数,并通过 从第二个参数开始依次传递参数 function func(food,drink){console.log(this)console.log(food)console.log(drink)…...
Django创建应用、ORM的进阶使用及模型类数据库迁移
1 Django项目创建第一个应用 Django 项目就是基于 Django 框架开发的 Web 应用,它包含了一组配置和多个应用,我们把应用称之为 App,在前文中对它也做了相应的介绍,比如 auth、admin,它们都属于 APP。 一个 App 就是一…...

tcpdump 如何使用
tcpdump 是一个在Unix和类Unix系统上运行的网络抓包工具,它用于捕获网络流量并将其转储到文件中以供后续分析。tcpdump非常强大,可以用于监控、调试和分析网络通信,用于排查网络问题以及安全审计。以下是关于如何使用tcpdump的详细介绍&#…...
goweb入门
创建gomod项目 go mod init web01新建main.go package mainimport ("fmt""net/http" )func handler(writer http.ResponseWriter, request *http.Request) {fmt.Fprintf(writer, "Hello World,%s!", request.URL.Path[1:]) } func main() {fmt…...

【python爬虫】批量识别pdf中的英文,自动翻译成中文下
不管是上学还是上班,有时不可避免需要看英文文章,特别是在写毕业论文的时候。比较头疼的是把专业性很强的英文pdf文章翻译成中文。我记得我上学的时候,是一段一段复制,或者碰到不认识的单词就百度翻译一下,非常耗费时间。之前的文章提供了批量识别pdf中英文的方法,详见【…...
YApi 新版如何查看 http 请求数据
YApi 新版如何查看 http 请求数据 因chrome 安全策略限制,在 cross-request 升级到 3.0 后, 不再支持文件上传功能,并且需要通过以下方法查看 network:1.首先在chrome 输入 > chrome://extensions打开扩展页2.开启开发者模式3.点击 cross…...

自动驾驶(apollo)
💓博主csdn个人主页:小小unicorn 🚚代码仓库:小小unicorn的代码仓库🚚 🌹🌹🌹关注我带你学习编程知识 自动驾驶技术 引言自动驾驶的基本原理自动驾驶的技术挑战自动驾驶的潜在影响结…...

web3.0涉及的技术
非同质化代币 非同质化代币(Non-Fungible Tokens,NFTs)是一种数字资产,与传统的加密货币(如比特币或以太币)不同,它们具有独特性和不可替代性。NFTs 是基于区块链技术的数字资产,用…...

26. 不相同的字符串(第一期模拟笔试)
题目:样例: 输入 1 abab 输出 2 思路: 这里的题目要求我们要最少操作删除次数,我们可以先统计每个字符个数,然后开始删除,每操作删除一次,就会产生一个新字符,ans r[i] >> 1…...

Rethink LSTMGRU
LSTM 设计思想 姑且不看偏置。 W W W 和 U U U 是加权的矩阵,写模型的时候用 nn.Linear(in_dim, out_dim) 就成; σ \sigma σ 是 Sigmoid 函数 第一条,遗忘门,定义为 有多少内容需要被遗忘;第二条:输入门…...
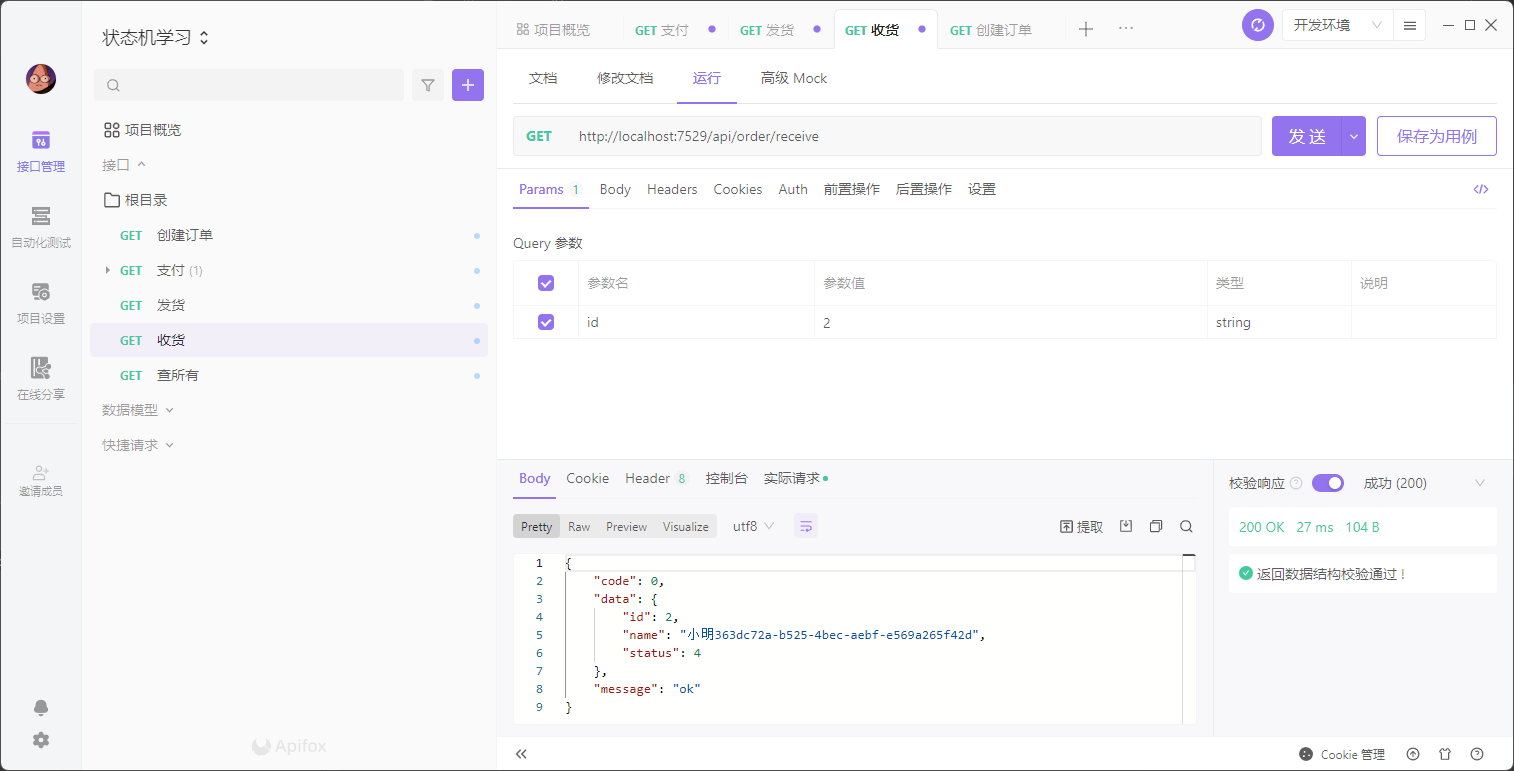
状态管理艺术——借助Spring StateMachine驭服复杂应用逻辑
文章目录 1. 什么是状态2. 有限状态机概述3. Spring StateMachine4. Spring StateMachine 入门小案例4.1 接口测试 5. 总结 1. 什么是状态 在开发中,无时无刻离不开状态的一个概念,任何一条数据都有属于它的状态。 比如一个电商平台,一个订…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
