【面试经典150 | 双指针】两数之和
文章目录
- 写在前面
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:暴力枚举
- 方法二:哈希表
- 方法三:二分法
- 方法四:双指针
- 知识回顾
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【双指针】【二分法】【哈希表】【数组】
题目来源
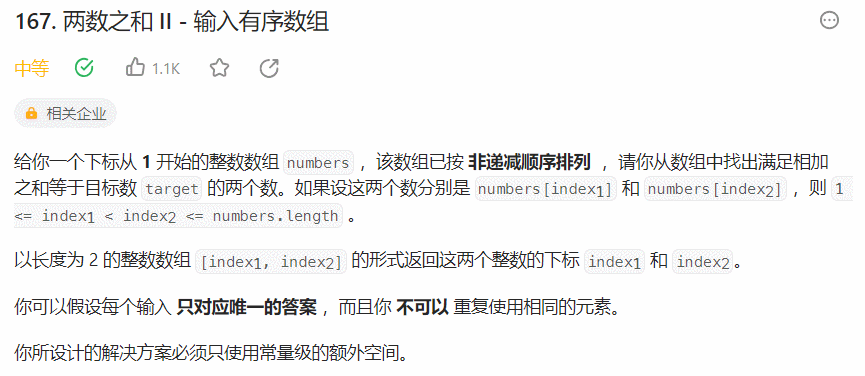
面试经典150 | 167. 两数之和 II - 输入有序数组
题目解读
给定一个下标从 1 开始按照 非递减顺序排列 的整数数组 numbers,找出两数之和等于 target 的两个数,返回它们的下标,其中每个整数只能使用一次,题目保证只有唯一的答案。
解题思路
本题属于基础题,与 1. 两数之和 解法基本一致。现在有三种解法如下。
方法一:暴力枚举
一个比较容易想到的方法就是枚举所有可能的两数组合,使用两层枚举,第一层枚举第一个整数,第二层枚举第二个整数。本题的数据量为 1 0 4 10^4 104,两层枚举的时间复杂度为 1 0 8 10^8 108,勉强可以通过。
具体地,在枚举中判断两数之和是否等于 target,如果相等,直接返回对应的下标。
因为每个元素只可以使用一次,并且两数先后出现的顺序没有要求,因此
第二层枚举的整数可以从第一层枚举的整数的后一个位置开始。
实现代码
class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {int n = numbers.size();for (int i = 0; i < n; ++i) {for (int j = i+1; j < n; ++j) {if (numbers[i] + numbers[j] == target) {return {i + 1, j + 1};}}}return {-1, -1}; // 本题保证一定有解,程序不会运行到此处}
};
但是实测中,最后几个测试用例超时了!
复杂度分析
时间复杂度: O ( n 2 ) O(n^2) O(n2)。
空间复杂度: O ( 1 ) O(1) O(1)。
方法二:哈希表
方法一中的时间复杂度可以优化到 O ( n l o g n ) O(nlogn) O(nlogn) 和 O ( n ) O(n) O(n),先来介绍时间复杂度为 O ( n ) O(n) O(n) 的方法,时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn) 的方法将在方法三中介绍。
我们在枚举第二个整数的时候,可以事先用一个哈希表来记录下所有整数以及位置,这样枚举第二个整数的时间复杂度可以降为 O ( 1 ) O(1) O(1),但是需要一个额外的空间。
具体地,可以先一次遍历 numbers,记录每个整数以及下标;记录完毕后,枚举第一个加数,在哈希表中查找第二个加数;以上的过程可以用一个循环就可以解决:枚举第一个加数之后,先在哈希表中查询有么有合适的第二个加数,然后再将当前的加数放入哈希表中,这样可以省去一次 for 循环。
实现代码
class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {unordered_map<int, int> idx;for (int i = 0; i < numbers.size(); ++i) {if (idx.find(target - numbers[i]) != idx.end()) {int idx1 = min(i, idx[target - numbers[i]]);int idx2 = max(i, idx[target - numbers[i]]);return {idx1 + 1, idx2 + 1};}idx[numbers[i]] = i;}return {-1, -1};}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为数组 numbers 的长度,只要一次循环就可以枚举两个加数。
空间复杂度: O ( n ) O(n) O(n),记录整数以及位置所用的空间。
方法三:二分法
在方法二中,我们是利用哈希表来降低枚举的线性时间的,我们还可以使用二分方法来降低线性枚举的时间复杂度。
前面两种方法中,都没有用到题目中 非递减顺序排列 这一条件,我们可以利用这种有序性进行二分查找第二个加数。
具体地,枚举第一个加数,假设下标为 i,接着要在 numbers[i+1,...,n-1] 中使用二分法查找 target - numbers[i],如果查找到直接返回两个加数的对应下标,否则继续枚举第一个数查找。
实现代码
class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {int n = numbers.size();for (int i = 0; i < numbers.size(); ++i) {int num1 = numbers[i];auto it = find(numbers.begin() + i + 1, numbers.end(), target - num1);if (it != numbers.end()) {int j = it - numbers.begin();return {i + 1, j + 1};}}return {-1, -1};}
};
复杂度分析
时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),枚举第一个数的时间复杂度为 O ( n ) O(n) O(n),在每次枚举中最坏需要二分查找 O(logn) 次,才能找到合适的第二个加数。
空间复杂度: O ( 1 ) O(1) O(1)。
方法四:双指针
以上三种都不是最优的,现在介绍时间复杂度和空间复杂度都是最优的方法——双指针。
初始左右两个指针 l e f t left left 和 r i g h t right right 分别指向 numbers 的第一个位置和最后一个位置。每次计算两个指针指向的整数之和,与 target 进行比较:
- 如果
numbers[left] + numbers[right] = target,直接返回{left + 1, right + 1}(因为下标从1开始); - 如果
numbers[left] + numbers[right] > target,则将right指针左移一位; - 如果
numbers[left] + numbers[right] < target,则将left指针右移移位。
为什么两数之和小了,右移 left 就可以了,右移 right 不可以吗?为什么两数之和大了,左移 right 就可以了,左移 left 不可以吗?
假设 numbers[i] + numbers[j] = target 是唯一解,其中 0 <= i < j <= n-1。初始时 left = 0、right = n-1,除非初始的时候,左右两个指针已经位于 i、j 处,否则一定是左指针先到达下标 i,或者右指针先到达下标 j:
- 左指针先到达下标
i时,右指针还在j的右侧,此时numbers[left] + numbers[right] > target,于是需要将right指针左移一位,这样才能缩小两数之和; - 右指针先到达下标
j时,左指针还在i的左侧,此时numbers[left] + numbers[right] < target,于是需要将left指针右移一位,这样才能增加两数之和。
于是,就有了以上所示的双指针更新规则。
实现代码
class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {int n = numbers.size();int l = 0, r = n - 1;while (l <= r) {int sum = numbers[l] + numbers[r];if (sum > target) {--r;}else if (sum < target) {++l;}else {return {l+1, r+1};}}return {-1, -1};}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n),双指针相向移动,它们 一共最多走 n 次。
空间复杂度: O ( 1 ) O(1) O(1),使用的额外变量只有两个指针。
知识回顾
今天来看看 C++ \texttt{C++} C++ 中二分查找的几个 API。
find() 使用二分法来查找数组中指定值的位置,其返回的是迭代器:
- 如果顺利查找到指定元素,则返回该元素位置迭代器;
- 如果没有查找到指定元素,则返回尾后迭代器;
通过位置迭代器与首位置迭代器作差可以得到该元素在数组中的位置。
lower_bound() 和 upper_bound() 的含义与用法可以参考 【二分查找】几种基本题型,你会了吗?。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 双指针】两数之和
文章目录 写在前面Tag题目来源题目解读解题思路方法一:暴力枚举方法二:哈希表方法三:二分法方法四:双指针 知识回顾写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢…...

桥接模式简介
概念: 桥接模式是一种结构型设计模式,它将抽象和实现分离,使它们可以独立地变化。通过使用桥接模式,可以将一个类的抽象部分与其具体实现部分解耦,并且可以在运行时动态地选择不同的实现。 特点: 将抽象…...
零钱兑换00
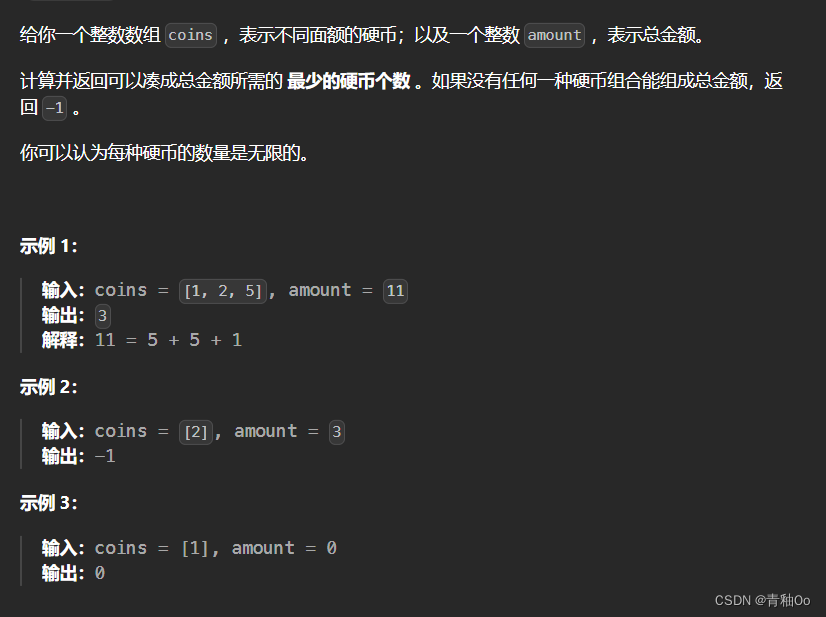
题目链接 零钱兑换 题目描述 注意点 如果没有任何一种硬币组合能组成总金额,返回 -1可以认为每种硬币的数量是无限的 解答思路 动态规划从总金额1开始推出目标金额所需的最少硬币个数,任意某个金额所需的最少硬币个数可以由当前金额减去每种面额的硬…...
JavaScipt中如何实现函数缓存?函数缓存有哪些场景?
1、函数缓存是什么? 函数缓存就是将函数运行的结果进行缓存。本质上就是用空间(缓存存储)换时间(计算过程) 常用于缓存数据计算结果和缓存对象。 缓存只是一个临时的数据存储,它保存数据,以便将…...
android studio的Android Drawable Preview
Android Drawable Preview 应用后,如下图: 再也不用一个一个点开去看了 其他学习资料: 1、付费专栏《Android kotlin入门到进阶系列讲解》:https://blog.csdn.net/qq_35091074/category_11036895.html 2、免费专栏《Android kot…...
基于云计算的区域LIS系统系统源码
在医疗机构内部,院内实验室主要负责本院临床科室的检验,院内LIS系统必须满足实验室日常的标本处理入库、仪器联机、检验结果处理、报告打印、报告发布、检验信息统计、检验信息报告发布、标本流程、外部医疗机构检验报告调阅等工作。 在医疗机构间&#…...

VR农学虚拟仿真情景实训教学演示
首先,VR农学虚拟仿真情景实训教学提供了更为真实的实践环境。传统的农学实训往往受制于时间、空间和资源的限制,学生只能通过观察或简单的模拟来学习农业知识和技能。而借助虚拟现实技术,学生可以进入虚拟农场,与各种农作物、工具…...
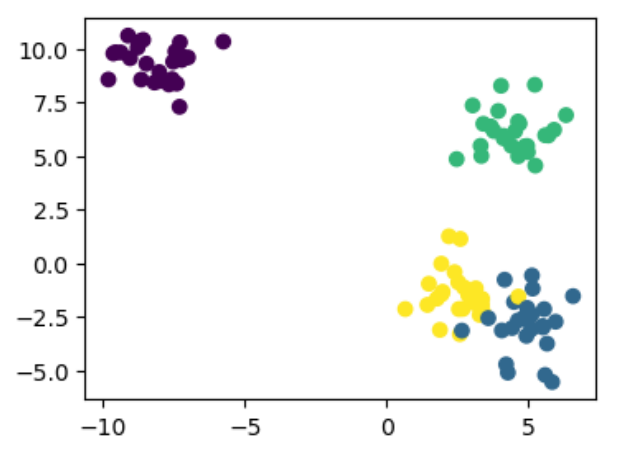
sklearn中make_blobs方法:聚类数据生成器
sklearn中make_blobs()方法参数: n_samples:表示数据样本点个数,默认值100 n_features:是每个样本的特征(或属性)数,也表示数据的维度,默认值是2。默认为 2 维数据,测试选取 2 维数据也方便进行可视化展示…...

Win11自带微软输入法怎么输入π及其他希腊字母
如果用搜狗等第三方输入法的话就没有这些问题了,各种符号很方便。 自带的输入法输入 pi 和 pai 都不能正常输入 π \pi π 参考文章 https://www.cnblogs.com/qq-757617012/p/14078133.html 如果用自带的输入法可以采用以下方式 输入uuxl xl表示“希腊”&#x…...

关于MyBatisPlus框架下出现xml里面定义的方法无法被正确识别以及提示调用mysql存储过程时参数无效的问题
第一个问题:xml里面明明定义了方法A,但是通过IService接口调用A的时候,总提示无法将接口中定义的函数绑定到xml中的同名方法中(“Invalid bound statement (not found): com.aircas.sqlservice.mapper.SysTempIndexMapper.getRemo…...

vscode路径别名文件跳转解决办法
第一步:下载 1.在jsconfig.json中配置: {"compilerOptions": {"target": "es5","module": "esnext","baseUrl": "./","moduleResolution": "node","p…...

layui 富文本编辑器layedit 以及 图片转base64前端页面显示
js var index layui.layedit.build(noticeInformationContent, {area: [500px, 400px],uploadImage: {url: NI/uploadconimage //接口url, type: POST //默认post},hideTool: [image]});layui.form.verify({content: function (val) {layui.layedit.sync(index);var content …...

服务器给前端实时推送数据轻量化解决方案eventSource+Springboot
一、前端代码 body代码 <div id"result"></div>js代码 $(function(){if(typeof(EventSource) ! "undefined"){var source new EventSource("/demo/getTime");source.onmessage function(event) {console.log(event.data);$(&qu…...
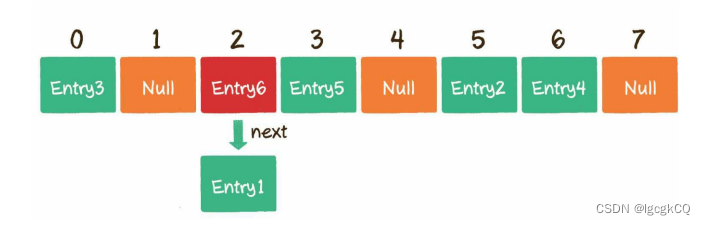
数据结构与算法:数据结构基础
目录 数组 定义 形式 顺序存储 基本操作 读取元素 更新元素 插入元素 删除元素 扩容 初始化 时机 步骤 优劣势 链表 定义 单向链表 特点 双向链表 随机存储 基本操作 查找节点 更新节点 插入节点 删除元素 数组VS链表 栈与队列 栈 定义 基本操作…...

virtualbox虚拟机中安装FreeDOS系统和DJGPP编译环境
一、安装FreeDOS系统 1、从官网下载FreeDOS系统镜像,下载的压缩包中包含两个文件:后缀为.iso和.img的镜像 下载页面 http://www.freedos.org/download/ 直接下载链接 https://www.ibiblio.org/pub/micro/pc-stuff/freedos/files/distributions/1.…...
JAVASE事件监听
代码: import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.util.ArrayList; import java.util.HashMap; import java.util.List; import java.util.Map; import java.util.Scanner;import javax.swing.JButton; import javax.…...
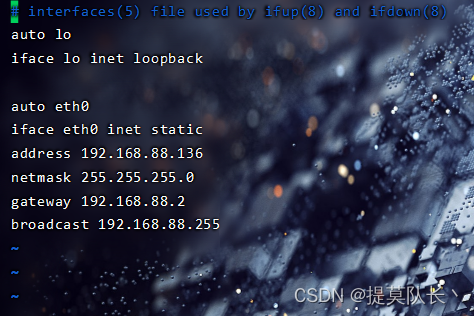
ubuntu14.04改静态ip
现在可能已经用ubuntu14.04的人已经不多了,这里讲一下Ubuntu14.04怎么改静态ip 第一步:输入ifconfig查看ip和子网掩码 第二步:输入route -n查看网关 上面ip是192.168.88.136,子网掩码是255.255.255.0,网关是192.168.…...
“文件的上传与下载:实现与优化“
目录 引言1.文件的上传2.文件的下载3. JRebel安装使用4. 文件批量上传总结 引言 在开发过程中,文件的上传与下载是常见的需求。本篇博客将以CSND为例,介绍文件上传与下载的常见方式,以及如何通过优化提升性能和用户体验。 1.文件的上传 使…...

uboot顶层Makefile前期所做工作说明三
一. uboot顶层 Makefile文件 uboot顶层 Makefile,就是 uboot源码工程的根目录下的 Makefile文件。 本文继续对 uboot顶层 Makefile的前期准备工作进行介绍。续上一篇文章内容的学习,如下: uboot顶层Makefile前期所做工作说明二_凌肖战的博…...

Mysql树形表的两种查询方案(递归与自连接)
你有没有遇到过这样一种情况: 一张表就实现了一对多的关系,并且表中每一行数据都存在“爷爷-父亲-儿子-…”的联系,这也就是所谓的树形结构 对于这样的表很显然想要通过查询来实现价值绝对是不能只靠select * from table 来实现的࿰…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
